初中数学教师说题例谈

福建省南霞中学　张和胜

初中数学教师说题例谈

福建省南霞中学张和胜

说题是一种教学教研活动，是一种有效的教学途径，也是一种促进教师专业成长的有效途径。说题活动的开展，不仅有利于提高教师素质，有利于教师教学理论与实践的结合，更有利于营造教师教研气氛。

初中数学说题方法

教师说题是类似于说课的一种教育教研展示和讨论活动，是说课的延续和创新，是一种深层次备课后的展示。说题活动往往和课堂教学实践活动结合在一起进行，通过“说”，发挥了说题教师的作用。通过课堂的具体实践，又使教师自身的教育理论得以提炼，也给评价者提供参考，集体的智慧得以充分发挥。说题者要努力寻求现代教育理论的指导，评价者也要努力寻求说题教师的特色与成功经验的理论依据，说评双方围绕着共同的课题形成共识，达到取长补短、优势互补的效果，说题者得到反馈，进而改进、提高和完善自己的教学方案；评价者从中得到比较、鉴别和借鉴，得到案例示范和理论滋养两方面的收益，营造了较好的教研氛围。

那么，实际说题活动中，教师该如何开展说题？说题有无固定的模式操作？又包括那几个常规步骤？本人认为说题要重点考虑四个方面，下面本人结合自身经验和一道例题谈谈具体的说题步骤和方法。

例：如图，点C是⊙O直径AB延长线上的一点，AB=4，点P是⊙O上的一动点（不与点B重合），连结CP，CP=OA.

（1）当点P为CE中点时，求△ACE的周长；

（2）是否存在四边形AOPE为梯形的情况，若存在，指出符合条件的图形的个数，并求出AE·EP值，若不存在，说明理由。

一、说命题立意

指明试题属于哪一能力层级立意，是感知、理解、分析、应用、迁移哪一层面的，所考查的知识能力是低阶思维还是高阶思维，试题在整个试卷中的难易程度是较易的，还是适中的还是偏难的，重点是要区分哪个群体的学生，如果有试卷的区分度等相关统计数据更好。

如：此题是一道以初中平面几何中圆的图形为背景，以三角形问题、梯形问题、相似问题及圆的问题为主干的几何综合题，本题旨在考查学生掌握双基情况的同时，重点考查学生综合运用初中几何知识及应用数学转化思想、数形结合思想、方程思想解决实际问题的能力，题目分三小题，入口较为简单，难度成螺旋上升趋势，总体难度较难，在达到考查目的的同时，也起到中考教学导向作用和中考选拔功能。

二、说知识考点

主要是分析考试大纲。分析试题是怎样体现考纲要求的，反过来说明考纲对这个问题是如何要求的。试题所要考查知识点属于哪种类型的知识。哪些是学生熟悉的，哪些是学生不熟悉的，学生在解题时存在什么困难，学生现有的知识发展区是什么，有待提高的发展区是什么。

如：本题第1小题考查切线的判定定理、勾股定理，第2（1）小题考查的是等腰三角形的性质、直角三角形的判定、勾股定理，第2（2）小题考查的是等腰三角形的性质及判定、梯形的判定、相似三角形的性质和判定的知识点，这些知识点是中考考试大纲明确要求学生掌握的内容，从所考的知识点看，几乎涵盖了初中平面几何所有重点，这些知识都是学生熟悉并能熟练运用的，但是题目通过圆的图形为基础，把这些知识点穿插到问题中，对学生综合运用知识的能力及分析问题、解决问题的能力提出较高要求，在实际解题中，可能因为审题不到位、知识点的理解不深刻而导致无法准确地判断而造成思维短路。如第2（1）小题的解题中学生对三角形中一边上的中线等于这边的一半的三角形是直角三角形这个定理理解不够，而造成辅助线无法作出陷入困境，而最后一小题则可能因相等线段的转化构造相似知识的缺乏，而走入由平行知识证明线段成比例的误区而无法自拔。

三、说讲解分析

这个步骤要求教师按类似于正常授课的情况给学生讲题，重点要解决好教学生如何读题、审题，理清题意，讲清解题思路、解题方法、解题技巧，板演详细的分析和解题过程，归纳题中涉及的知识点、思想方法、难点易错点、解题误区，拓展一题多解、一题多变、多题一解等。简单地说就是处理好三个关系即：题目有什么？该如何解？还能怎么解？

如：第1小题题目告诉了我们什么？由已知可得CP=OA=2,OC=2,要证明CP为切线，而点P已经在圆上，根据切线的判定定理必须连结OP（如图1），并证明OP⊥CP，由线段长到直角，联系勾股定理逆定理而证明。还能怎么解呢？要证垂直就要90°角，图中有吗？可以构建吗？从直径所对圆周角为90°想到什么？尝试连结AP、PB（如图2）可证明吗？由观察发现只要证明∠CPB=∠A=∠APO,也可得OP⊥CP，从而把问题转化为证明△CPB∽△CAP，进而从条件得CP2=CB·CA可证。

图1

图2

图3

图4

第2（1）小题的关键是画出符合题意的图形（图3），由已知新增条件可得OP= CP=PE=2,从而可得△OEC为直角三角形，可求出而得周长为

第2（2）小题题目条件把“点P为EC中点”改为条件“四边形AOPE为梯形”，由于四边形字母顺序已经确定，故点P必在线段EC上，由CE与AC不平行，四边形为梯形仅有OP∥AE的情况（如图4），故存在，并由圆的对称性可得符合条件的图形有2种情况，又由求AE·EP的值可知问题与相似问题、半径为2有关，由OP=PC，OP∥AE，易证EA=EC，故求AE· EP的转化为求EC·EP的值，又从条件易得∠1=∠C，从而由△EPO∽△ECO得EO2=EC·EP=AE·EP=4得解，本题也可从条件中得到△OEC为等腰三角形，进而求OC=EC=AE，又OP∥AE，根据平行线分线段成比例定理得CP：PE=OC：AO，得OC·PE=CP·AO=4，得AE·EP=4.

四、说解题反思

探究所说试题的拓展价值，开展“后建构活动”。让学生由现有发展区，继续提高。拓展迁移，或把解此题的规律推广，或把解此题一般规律推广到特殊规律，或把解此题的特殊规律推广到一般规律。具体操作，可以改换试题的相应条件，形成新的变式试题，或是找出同类试题。

如：解完本题，我们再次反思本题，分析发现以下几个要点：

1.本题三个小题之间联系密切，第1小题中的第2种解法和第2（2）小题的第2种解法相同，起到首尾呼应的效果。

2.我们可从本题中进一步加深了对初中几何常见图形结论的理解和应用，即当有共点线段积出现时，可构造如图5的模式求解,即当PC2=PA·PB时，△PCA∽△PBC，得∠1= ∠B；反之当∠1=∠B时，△PCA∽△PBC 得PC2=PA·PB；

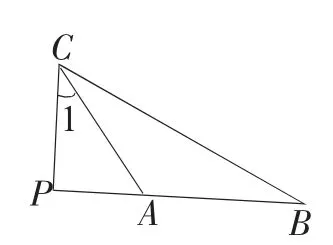
图5

3.由第2（1）的解题其实还可以得到特殊角，即（如图3）∠C=30°，∠A=45°；而第2（2）小题的解题中我们也可得到特殊角∠C=∠A=36°，也就是说第2（2）题其实含有5个等腰三角形，若有这样我们还可求出图4中每一条线段的长度。

4.结合上面第3点的分析，我们是否可以这样认为，为了使本题的第2题更有延续性和对称性，最后一小题改为：当点P为圆弧CE中点时，求△APC的周长，若考虑题目难度值也可改为求∠C的度数和△APC的周长，这样给出暗示让学生相对容易找到解题突破口。

5.其实本题还有一个审题关键点，就是第2小题题目条件为“若直线CP 与⊙O 的另一个交点为E，这里明确了CP为直线并非线段，若把条件去掉，则可能出现点E在线段CP上的情况（如图6）这种图形情况，则第2（2）小题可问：以点A、O、P、E四点围成四边形为梯形有几种情况，那答案将会出现4种，也许命题者考虑到后续求值而没有把这种情况纳入考查。