基于分形接触理论的拉杆转子固有特性研究
齐 琛, 张锁怀
(1.陕西科技大学 机电工程学院, 陕西西安 710021; 2.上海应用技术大学 机械工程学院, 上海 201418)
基于分形接触理论的拉杆转子固有特性研究
齐 琛1, 张锁怀2*
(1.陕西科技大学 机电工程学院, 陕西西安 710021; 2.上海应用技术大学 机械工程学院, 上海 201418)
通过分形接触理论,建立了分布式拉杆转子轮盘接触刚度模型,对轮盘接触面的法向和切向接触刚度进行了计算,分析了接触刚度随轮盘面粗糙度和拉杆预紧力的变化规律;在此基础上,建立了考虑轮盘接触效应的拉杆转子动力学模型,通过固有特性研究,得到其固有频率和振型.分析发现,拉杆转子随表面粗糙度的减小和拉杆预紧力的增大,其整体刚度和固有频率都有所提高;预紧力较小时,固有频率上升速度快,随着预紧力的增加固有频率上升速度缓慢,且粗糙度越小固有频率越大.
拉杆转子; 分形接触刚度; 模态分析; 固有频率
0 引言
在大型动力系统、旋转机械中大部分故障都是由于转子的振动造成的[1,2],因此工程中对转子本身的固有振动特性以及振动成因非常关心.现代大型燃气轮机转子多以拉杆转子为主,而燃气轮机出现的故障也多以转子为主[3].拉杆式转子是通过拉杆螺栓将各级轮盘压紧在一起,使构成的转子具备重量轻、刚度高、强度好、易于拆装、热容量小等优点.这种转子已不再是一个连续的整体结构,各轮盘之间的接触效应对拉杆转子的动力学特性产生了一定影响[4].以往对这类转子进行振动计算分析时,多简单地以整体转子对待,或用刚度修正系数的办法处理,缺乏一个合理的力学模型,因而用这些方法计算出来的转子各阶固有频率值均不理想[3].近年来,有学者建立了考虑接触效应的拉杆转子动力学模型,分析其动力学特性[5-8],以及通过实验研究拉杆转子[9,10],但大多是从接触体的宏观特性着手来建立接触面的力学模型[3,11-13](如Hertz接触模型、G-W模型),模型依赖于传统的粗糙面统计参数(如微凸体高度均方差等),而这些统计参数与测量长度和仪器分辨率有关,不具有尺度独立性,因此会影响拉杆转子的准确建模和后续分析.
针对上述研究工作的缺陷和不足之处,本文重点考虑拉杆转子轮盘-轮盘结合面间的接触效应,从材料表面微观特征的分析着手,运用分形接触理论对拉杆转子接触刚度的计算问题进一步深入研究,得到拉杆转子结合面的力学模型,进而建立拉杆转子的动力学模型,分析预紧力和粗糙度对拉杆转子固有振动特性的影响.
1 轮盘表面接触模型
1.1 轮盘表面法向接触刚度分形模型
根据文献[14]对分形接触理论模型的研究成果,有如下经验公式:
(1)
(2)
式(1)、(2)中:Ra-表面粗糙度;D-粗糙表面的分形维数;G-粗糙表面的分形粗糙度参数.
由文献[15,16]的分形接触理论模型知,结合面法向接触刚度便可以由下式来计算:
(3)
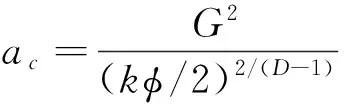

式中:al-最大的接触点面积;ac-临界接触面积;H-较软材料的硬度;σy-较软材料的屈服强度;E-两接触材料的复合弹性模量;E1、E2和v1、v2分别为两个接触材料的弹性模量和泊松比.
又可知粗糙表面上的法向力P与最大接触点的面积al之间的关系为:
当1 (4) 当D=1.5时,接触载荷为: (5) 1.2 轮盘表面切向接触刚度分形模型 根据文献[15,16]的分形接触理论模型,结合面的切向接触刚度可由下式计算(设切向力为零): (6) 1.3 计算结果与讨论 研究的模型拉杆转子如图1所示,长度为1 086 mm,小轮盘直径为140 mm,大轮盘直径依次是194 mm、214 mm、238 mm,转子材料为45号钢,轮盘表面参数为表1所示. 图1 拉杆转子模型 表1 转子轮盘表面参数 由公式(3)和(6)可知,接触刚度仅与拉杆预紧力和轮盘接触表面粗糙度有关,为了比较轮盘接触面的粗糙度和不同预紧力对接触刚度的影响,选取表面粗糙度依次为0.4μm、0.8μm、1.6μm、3.2μm、6.3μm、12.5μm、25μm和50μm,拉杆预紧力从100~1 000 N,结合表1数据进行数值仿真计算,结果见图2和图3所示. 图2 法向接触刚度值 图3 切向接触刚度值 由该模型结果得到的主要结论如下:法向载荷增大时,结合面的法向和切向接触刚度增大,这是因为随着法向载荷增大,结合面的实际弹性接触面积增大,其承受切向载荷的能力也将增大,从而其法向、切向接触刚度增大;拉杆转子的接触刚度随表面粗糙度降低而增大,并且刚度值增加的速度与表面粗糙度有关,粗糙度越低,表面越光滑,轮盘接触面积越大,抵抗接触变形的能力越强,则增长越快. 2.1 转子建模 拉杆转子由八根拉杆、十三个空心盘和两个轴头组成,轮盘之间具有一对接触面,三维模型如图4所示. 图4 拉杆转子三维模型 将结合面接触刚度分形模型计算结果以接触弹簧单元模式嵌入拉杆转子的有限元模型,进行模态分析.拉杆转子不再是一个连续的整体,在拉杆转子的结构中,轮盘之间的接触耦合、拉杆螺栓的预紧力通过轮盘之间的接触面进行传递,并且摩擦接触面还保证轮盘之间在横向位移一致.三维模型中轮盘采用柔体-柔体的面-面接触,接触面上采用CONTAC174 和TARGET170单元建立接触对,并采用绑定接触设置,即选择KEYOPT(12)=4不分离接触,其中接触积分点或初始在球形区域内,或一旦接触就总是与目标面沿接触面的法向连在一起,但允许滑动,程序通过相同的实常数号来识别每一个接触对,接触算法选择增强拉格朗日算法.轮盘通过拉杆预紧力组合在一起,通过调整螺栓的预紧力可以改变转子的接触刚度,对模型转子进行自适应网格划分,得到拉杆转子的有限元模型如图5所示,接触面示意图如图6所示. 图5 拉杆转子有限元网格约束模型 图6 拉杆转子接触面 2.2 计算结果分析 通过添加上述一系列法向、切向接触刚度值,经有限元模态分析后得到模型转子的前10阶固有频率及对应模态振型,由于分析时约束为模型转子两端面的轴向移动,转子会发生沿X轴和Y轴的刚体位移运动以及绕Z轴的回转运动,故结果中的前三阶固有频率近似为0,略去前三阶固有频率. 由于篇幅有限,本文仅列出模型转子的第四阶到第六阶频率随预紧力、粗糙度的变化规律,如图7~9所示,对应的振型图如图10~12所示. 图7 第四阶模态频率 图8 第五阶模态频率 图9 第六阶模态频率 图10 第四阶振型图 图11 第五阶振型图 图12 第六阶振型图 从图7~9中的固有频率可知:拉杆预紧力和表面粗糙度对分布式拉杆转子的固有频率有明显的影响.其影响规律为:随着预紧力不断提高和表面粗糙度的降低,模型转子的固有频率也相应上升.上升趋势为:预紧力较小时上升的速率快,随着预紧力的增加上升的速率变缓慢,且粗糙度越低,固有频率越大. 这是因为:在拉杆预紧力作用下,圆盘端面相互接触时,最先接触的是圆盘端面微观不平整表面最高的凸峰部分,也就是微观粗糙度最大值部分.随着预紧力的继续增加,那些未参与接触的微凸体也陆续进入接触状态,并产生变形.当预紧力越来越大时,进入接触的微凸体越来越多,实际接触面积越来越大,压强反而变小,因此,变形率越来越小.其宏观表现就是轮盘端面法向接触刚度、切向接触刚度增加,固有频率刚开始时提升速率快,后来逐渐变缓. (1)根据分形接触理论得到了不同粗糙度和不同载荷作用下的法向和切向接触刚度,为准确进行计入接触刚度影响的拉杆式转子动力分析奠定了基础. (2)随着拉杆预紧力增大,拉杆转子的各阶固有频率也有所增大.预紧力较小时,固有频率增加较快,随着预紧力的增加,固有频率增长速度逐渐变缓,粗糙度越小,接触刚度越大,转子固有频率越高.参考文献 [1] 王 荻,喻志强.MS6000B型燃气轮机组振动故障分析及处理[J].广东电力,2003,16(2):29-30,62. [2] 巩桂亮,喻志强.MS6001B燃气轮机发电机组轴向振动故障的分析处理[J].华东电力,2003,31(5):45-48. [3] 饶柱石.拉杆组合式特种转子力学特性及其接触刚度的研究[D].哈尔滨:哈尔滨工业大学,1992. [4] 施丽铭,张艳春.拉杆式模型转子固有频率的实验与计算研究[C]//第8届全国转子动力学学术讨论会论文集.湘潭:中国振动工程学会转子动力学专业委员会,2008:47-49. [5] 黄 锐,邓 博.国内外燃气轮机转子结构特点及9FA型燃气轮机的模态分析[J].中国电力教育,2006(S3):60-64. [6] 高 锐,袁 奇,高 进.燃气轮机拉杆转子有限元模型研究及临界转速计算[J].热能动力工程, 2009,24(3):305-308,408. [7] Kim S M,Ha J H,Jeong S H,et al. Effect of joint condition son the dynamic behavior of a grinding wheel spindle[J].International Journal of Machine Tools & Manufacture,2001,41(12):1 749-1 761. [8] Lu Mingjian,Geng Haipeng,Xu Guohui,et al.Analytical and experimental study of dynamic characteristics of rod fastened rotor-bearing system under preload saturation[R].San Antonio,TX,United States:ASME Turbo Expo 2013:Turbine Technical Conference and Exposition,2013. [9] 施丽铭,张艳春.拉杆式模型转子固有频率的试验与研究[J].振动与冲击,2008,27(8):47-49. [10] 施丽铭,张艳春.燃气轮机转子模态试验与分析[J]. 燃气轮机技术,2007,20(4):47-49. [11] 何 鹏.分布式拉杆转子动力学特性分析[D].哈尔滨:哈尔滨工业大学,2009. [12] 骆 舟.综合接触效应的盘式拉杆转子轴向振动与扭转振动动力学特性研究[D].长沙:中南大学,2008. [13] Yuan Qi,Gao Rui,Feng Zhenping,et al.Analysis of dynamic characteristics of gas turbine rotor considering contact effects and pre-tightening force[C]//Proceedings of ASME Turbo Expo.2008:Power for Land,Sea and Air.Berlin:American Society of Mechanical Engineers,2008:983-988.. [14] 方 兵.精密数控机床及其典型结合面理论建模与实验研究[D].长春:吉林大学,2012. [15] 张学良,黄玉美,傅卫平,等.粗糙表面法向接触刚度的分形模型[J].应用力学学报,2000,17(2):31-35,144. [16] 张学良,温淑花,徐格宁,等.结合部切向接触刚度分形模型研究[J].应用力学学报,2003,20(1):70-72,162. 【责任编辑:蒋亚儒】 Study on natural characteristic of the rod fastening rotor based on fractal contact theory QI Chen1, ZHANG Suo-huai2* (1.College of Mechanical and Electrical Engineering,Shaanxi University of Science & Technology, Xi′an 710021, China; 2.School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 201418,China) Establish the contact stiffness model of the distributed rod fastening rotor using the fractal contact theory to calculate the normal and tangential contact stiffness,analyse the variation tendency of the contact stiffness along with the surface roughness and the pre-tightening force;further,set up dynamic model of the rod fastening rotor take into account the contact effect of the wheel and obtain the natural frequency and mode shape through the natural characteristic research.The analysis result is the decrease of the surface roughness and the increase of the pre-tightening force,the overall stiffness and natural frequency has improved;pre-tightening force is small, the speed rising fast,with the growth of the pre-tightening force speed is slow,and the lower the roughness natural frequency is greater. rod fastening rotor; fractal contact stiffness; modal analysis; natural frequency 2016-06-12 国家自然科学基金项目(51475311) 齐 琛(1990-),男,河北衡水人,在读硕士研究生,研究方向:机械系统动力学 张锁怀(1962-),男,陕西宝鸡人,教授,博士,研究方向:机械系统动力学,zhangsuohuai@263.net 1000-5811(2016)06-0160-04 TB123 A





2 拉杆转子的有限元模态
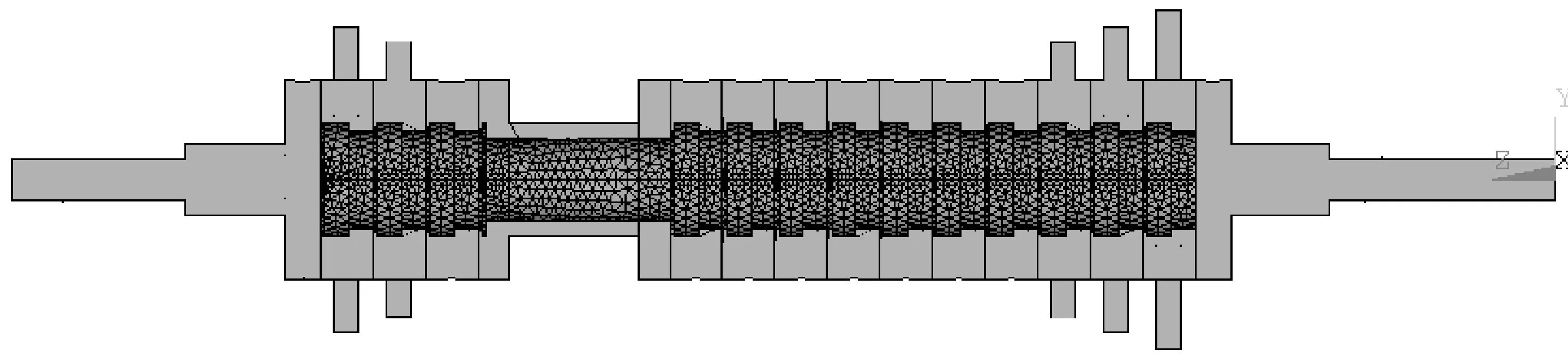

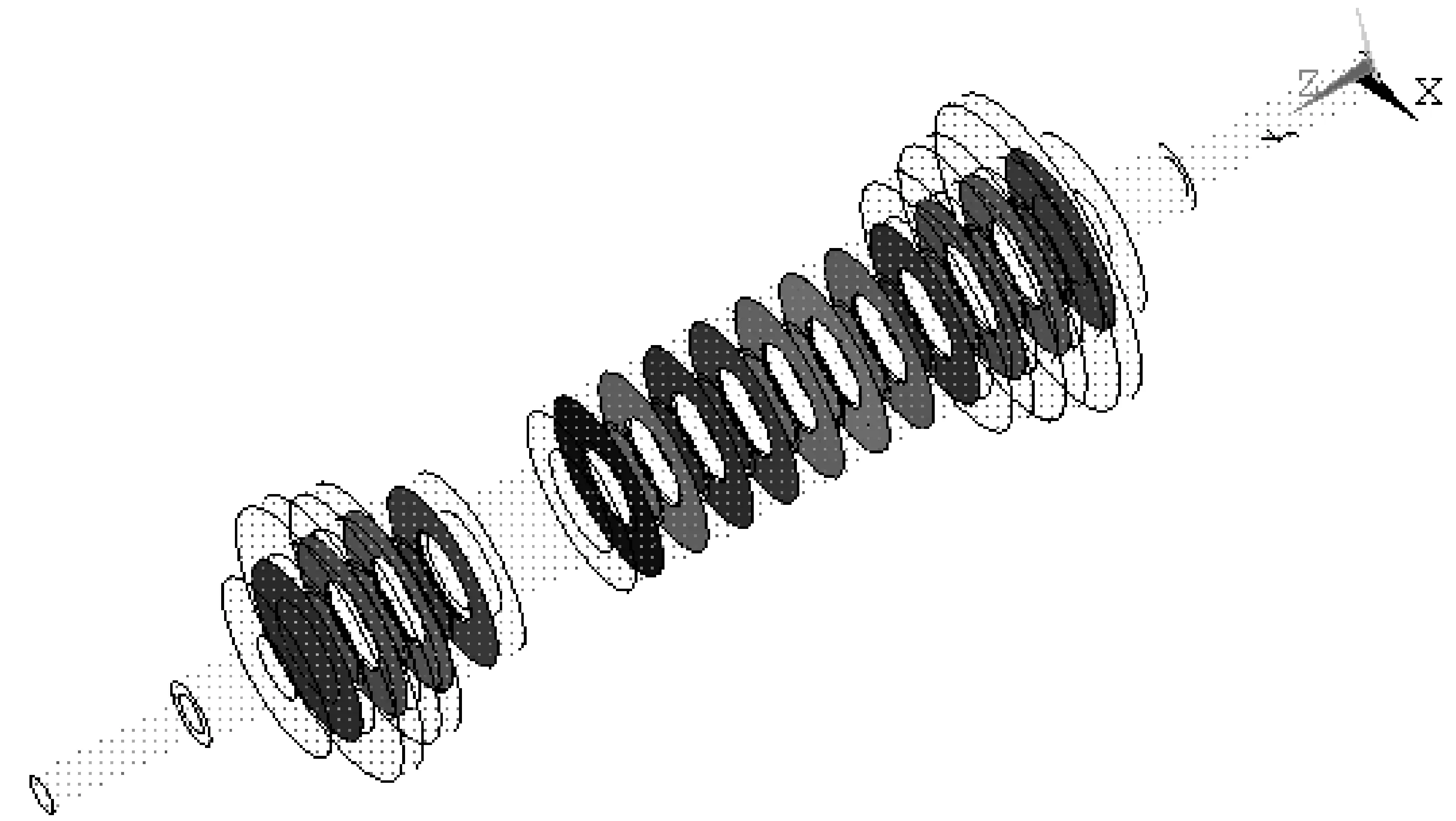






3 结论

