基于叶圣陶教育思想下中职数学问题教学模式

江苏省张家港中等专业学校 张志开

基于叶圣陶教育思想下中职数学问题教学模式

江苏省张家港中等专业学校 张志开

本文以叶圣陶教育思想为指导，结合教学实例，从创设问题情境、设计探究任务、营造猜想氛围三方面探讨了基于问题教学的中职数学有效教学策略，以期能启迪学生思维，实现学生的“自奋其力，自致自知”。 这正是叶圣陶先生提出的“帮助学生学习”的精辟思想所在。

中职数学 叶圣陶教育思想问题教学

“师者，所以传道、授业、解惑也”，这句古语一度成为教师对自己角色定位的追求。然而在新课改下，教师不仅仅只是课堂上的传道、授业和解惑，更要帮助学生学会学习，激发学生学习的自主性。正如叶圣陶先生所说：“我意如能令学生于上课之时，主动求知，主动练习，不徒坐听教师之讲说，即为改进教学之一道。”叶老顺应时代要求，精辟地道出了教师在新课改理念下的主导作用，尤其是在“问题教学”中，从提出问题、分析问题到最后的解决问题，都需要教师能够发挥主导作用，启迪学生思维，从而引导学生自己去发现和解决问题，这正是叶圣陶先生提出的“帮助学生学习”的精辟思想所在。

一、创设问题情境，鼓励学生提出问题

在数学思维活动中，培养学生的问题意识是一个重要环节。学生是学习的主体，而学习是学生自己的事情，任何人都不可能替代学生去学习、去思考、去掌握规律。作为课堂的主导者，教师应积极创设问题情境，唤醒学生的主体意识，让学生自己去发现问题，从而激发学生学习的内在动机，强化学生的主体地位。

例如，在学习“椭圆的定义和标准方程”这一内容时，教师可以创设问题情境，引导学生自主动手探究，发现并提出问题。首先，提供一块纸板、一段无弹性的细绳和两枚图钉，让学生在小组内动手拉紧细绳，并观察移动笔尖后所得的轨迹。在反复实践后学生就会很自然地产生疑问，如：为什么图钉距离太远没办法画？图钉怎么放才能画出椭圆？绳子的长短和图钉的距离有没有关系？为什么有的学生画得扁一些，有的画得圆一些？这样的问题情境使学生通过动手实践探究出可以将圆心从一点“分裂”成两点，只要将这一段细绳的两端固定于“分裂”出的这两点之上，可画出椭圆。并在教师动态演示的基础上引出椭圆定义，从具体实例中经历椭圆概念的产生过程，可以有效激发学生的学习内在动机，为接下来对椭圆的深刻认识，探究椭圆的标准方程作好铺垫。

一个好的问题情境，可以有效激发学生探究的欲望，在富有吸引力的问题情境中掌握数学概念的本质。

二、设计探究任务，培养学生发现问题的能力

在问题教学中，教师根据学生的学情设计探究任务，放手让学生自己去发现和探究，自主分析任务中的关键要素，从而发现问题，诱导学生综合已有的数学知识，寻找出其中的关键，最后在教师的点拨和引导下，建立正确的数学模型。

例如，在教学“一元二次不等式的解法”时，我结合本校的服装专业，以为工作台设计台布为例，让学生按照一定的条件求出台布下垂长度的范围，即要求解一元二次不等式2x2+5x-3≤0，此时设计探究任务：一元二次方程、二次函数均含有类似此不等式左边的二次三项式，那么，能不能利用二次函数的图像、二次方程的解来求解二次不等式？让学生带着问题在小组内进行合作探究，这样学生经过讨论与交流后会发现：二次方程2x2+5x-3＝0的两个不等的实数解对应着二次函数y=2x2+5x-3图像与x轴交点的横坐标。同时学生也会产生新的疑问：二次不等式的解集与二次函数的图像到底有何关联呢？随着这一疑问的提出，课堂也进入了高潮阶段。教师顺势点拨：引导学生仔细观察二次函数的图像，y>0时，图像在x轴上方，y<0时，图像在x轴下方，得出二次不等式的解集与二闪函数的图像在坐标轴中的位置有着特殊的关联。这一知识点也正是本课的难点所在。

可见，教师以任务探究的形式，加上适时的关键点拨，使学生形成了认知冲突，学生在寻找着数学间的联系，通过自身知识把二次方程的解、二次函数的图像构建成二次不等式解集的数形结合的模型。

三、营造猜想氛围，培养学生的问题意识

“教是为了不教”是叶圣陶教育思想的精髓，许多成功的教学先进典型，无一不是这一精髓的有效例证。而猜想正是让学生面对一个问题时提出各种可能的假设，这需要学生积极思维，自始至终都能以饱满的热情参与数学知识的探索过程，才能在猜想、验证、确定的过程中让学生自主获取知识，实现学生学习力的提升。

例如，在教学“两角和与差的正切公式”时，我出示了如下一组求值题：

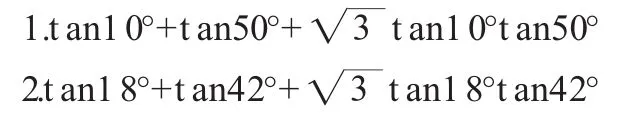
训练结束后，有学生提出：能否得到一般性的结论？这时，我没有立即回答该生的问题，而是鼓励学生根据自己所学的知识大胆猜想下，有学生说：а+β+60°，则tanа+tanβ+tanаtanβ=成立，也有的学生提出若三角形内角分别是 а、β、γ，则tanа+tanβ+tanγ=tanаtanβtanγ成立。数学是一门严谨的学科，从思考、分析到解题的过程都应是缜密全面的。因此，我让学生自主去验证上述两个猜想，共同证明。

在问题教学中，教师应营造猜想氛围，让学生善于抓住灵感，勇于大胆猜想，从而培养学生善提问题的能力，在猜想中学会研究，学生的创造潜能才能得到最大限度的发挥。

问题是数学的心脏。在中职数学教学中积极践行问题教学法能够为学生提供一个发现、创新的机会和平台，对素质教育的实施具有积极的意义。我们中职数学教师应以叶圣陶先生为榜样，身体力行，躬行实践，学习叶老的精神，学习叶老的教育思想，在课堂这一主战场上，以自己的“相机诱导，随机点拨”，实现学生的“自奋其力，自致自知”。