高中数学教学策略——复习课的视角
☉广西柳州高级中学 吴佐慧
☉湖北大学 刘合国
高中数学教学策略——复习课的视角
☉广西柳州高级中学吴佐慧
☉湖北大学刘合国
一、引言
波利亚认为数学课的目的是教会年轻人思考,不仅要教学生证明问题、提出问题,甚至也要教他们猜想问题.我们作为一线数学教师,更应该贯彻这种思想.在数学教学过程中,注重各种知识内在联系的同时也要注重教学策略.在课堂教学中,教师应用适当的教学策略对知识进行加工重组,引导学生去发现问题、解决问题,培养学生的问题意识并激起学生的求知欲,以引起学生对数学的兴趣,进而不断提高数学教学的效率.
本文将从复习课的视角对如何注重教学策略加以解读.在日常教学中,很多老师觉得复习课很难上,关键是复习课上的知识点都是已经学过的,教学设计得不好就很难激起学生的兴趣及求知欲.所以复习课上,我们的主要任务是引导学生对所学数学知识进行系统的归纳整理.通过问题引入、题型设计建立起不同题型、知识的联系,让学生有全新的认识,不断提高他们分析问题、提出问题、解决问题的能力,并有意识地培养他们科研、创新的能力,为更高层次的学习打下坚实的基础.
复习课不是死记硬背课,不是机械重复课,不是表演课.所以我们在教学时,要准确地把握教学要求,循序渐进地教学,不能搞一步到位,要追求通性通法,不追求特技.“数学根本上是玩概念的,不是玩技巧,技巧不足道也!”同时我们更应该注重教学策略,注重“数学情境与提出问题”的教学,找好问题,把更多的注意力放在核心概念、基本数学思想方法上,不断地提高中学数学的教学效率与教学质量.但只有教育工作者自身真正地理解好数学,才能不断地使学生体会到数学简洁、自然的特性,才能使学生养成良好的思维习惯.
二、实例
本部分通过对递推数列通项公式的教学设计,具体地展示应如何应用合适的教学策略引导学生去思考问题,去进行总结归纳.
关于递推数列的教学,高中老师常见做法是归纳题型、总结技巧、印发学案,让学生被动接受,以后再生搬硬套.这样归纳题型,诚然有其应试的好处,但学生并不知道其来龙去脉,并不能弄清楚为什么要这样出题.所以在教学中,如果没有以思想方法为主线,就会显得杂乱无章.学生只能死记硬背,若题型稍微有些变化,很多学生就没有思路,没有方法了.
数列题型很多,大部分学生不知道其来历,只是一味地死记硬背,这样的效果可想而知.所以在教学过程中,要追根溯源,讲解每种方法的来历及其相互关联.不要怕花时间,也只有在这上面花的时间到位了,学生的理解就会更透彻,记忆就会更长久.
达到这样效果的重要前提就是授课教师能理解数学问题的本质,并发现问题之间的相互关联.只有这样才能使学生学得轻松,才能使学生体会到数学自然、简洁的魅力.接下来就以数列递推关系式为例给出教学设计.
数列可以看作一个定义域为正整数集N*(或它的有限子集{1,2,…,n})的函数,当自变量从小到大依次取值时,对应的一列函数值,而数列的通项公式也就是对应函数的解析式.所以在数列教学过程中要不断体现并强化这种函数的思想.用函数的观点认识数列,通过化归来分析处理数列问题.
先引导学生回顾中学阶段所学过的函数类型:常数函数、一次函数、二次函数、高次函数、反比例函数、指数函数、对数函数、三角函数等.在后面的教学中我们会发现几乎所有题型都是在这些函数中变形.
问题A1若数列{an}满足an-an-1=1(n≥2),a1=1,求通项公式an.
解:因为an-an-1=1(n≥2),所以a2-a1=1,a3-a2=1,…,an-an-1=1.由累加法可得an-a1=(n-1)×1,则an=n.
因为a1=1也满足上式,所以an=n.
本题的方法很多,可直接把数列{an}当成等差数列来求解,我们也可以用上面的方法,通过这种方法再次回顾等差数列通项公式的一种推导方法:累加法.
接下来引导学生思考,在问题A1中an=an-1+1(n≥2),其中“1”是常函数,那我们能不能把它换成已经学过的其他函数?比如一次、二次、指数、对数函数等.
问题A2若数列{an}满足an=an-1+n(n≥2),a1=1,求通项公式an.
解:因为an-an-1=n(n≥2),所以a2-a1=2,a3-a2=3,…,an-an-1=n.由累加法可得an-a1=2+3+…+n,

问题A3若数列{an}满足an=an-1+n2(n≥2),a1=1,求通项公式an.
解:因为an-an-1=n2(n≥2),所以a2-a1=22,a3-a2=32,…,an-an-1=n2.由累加法可得an-a1=22+32+…+n2,

问题A4若数列{an}满足an=an-1+n3(n≥2),a1=1,求通项公式an.
解:因为an-an-1=n3(n≥2),所以a2-a1=23,a3-a2=33,…,an-an-1=n3.由累加法可得an-a1=23+33+…+n3,

注1:通过问题A3和问题A4,复习一下an=n2以及an=n3的前n项和公式.
问题A5若数列{an}满足1,求通项公式an.
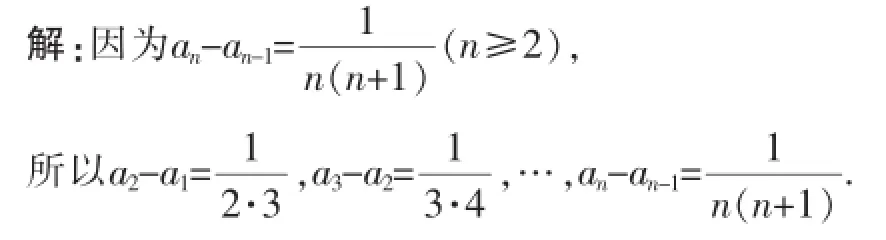
又因为a1=1也满足上式,所以
注2:通过问题,引导学生复习裂项相消法,例如:

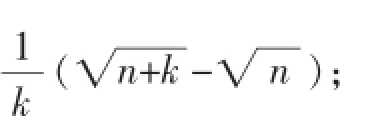
问题A6若数列{an}满足an=an-1+2n(n≥2),a1=1,求通项公式an.
解:因为an-an-1=2n(n≥2),所以a2-a1=22,a3-a2=23,…,an-an-1=2n.由累加法可得an-a1=22+23+…+2n,
所以an=1+22+23+…+2n=2n+1-3.
又因为a1=1也满足上式,所以an=2n+1-3.
小结1:能用累加法的数列{an}要满足an=an-1+f(n)(n≥2)的形式,且f(n)在现有知识水平下能求和.同学们自己也可以编出很多类似的习题.
在类型A中,an与an-1前的系数均为1,如果an与an-1前的系数不相等,又该如何处理?
问题B1若数列{an}满足an+1=2an+1,a1=1,求通项公式an.
解:因为an+1=2an+1,所以an+1+1=2(an+1),因此数列{an+1}是首项为2,公比为2的等比数列,所以an+1=2n,故an=2n-1.
问题B2若数列{an}满足an+1=2an+3,a1=1,求通项公式an.
解:因为an+1=2an+3,,所以an+1+3=2(an+3),因此数列{an+3}是首项为4,公比为2的等比数列,所以an+3=4·2n-1= 2n+1,故an=2n+1-3.
注3:在问题B1与B2中,an前面的系数是2,则可以通过“拼凑”转化为一个新的等比数列再进行求解,但是如果不是2,拼凑就有些烦琐.
(3)对数裂项:
问题B3若数列{an}满足an+1=3an+1,a1=1,求通项公式an.
在解决这个问题之前,我们注意观察:在问题B1与B2的解答过程中,拼凑得到的结构有什么共性?对解决问题B3有什么启发?
问题B1与B2均可转化为an+1+t=2(an+t),那么问题B3能不能也应用类似的思想?不难发现:若an+1+t=3(an+t),则an+1=3an+2t与原等式an+1=3an+1比较可得2t=1,所以原等式变为因此数列}是首项为,公比为3的等比数列,所以·3n-1,故an=
以上方法即为待定系数法.我们通过引入一个参数t,就把问题转化成基本的等比数列求解,其中用到了化归的思想,即把一个新的问题转化归结为我们所熟悉的问题加以求解.
小结2:形如an+1=pan+d(p≠1)均可用待定系数法来求解.上式中的d是常数,沿用前面的思路,d能否换成类似的一次函数、指数函数呢?
问题B4若数列{an}满足an+1=4an-3n+1,,a1=2,求通项公式an.
解:应用待定系数法,令an+1+a(n+1)+t=4(an+an+t),即an+1=4an+3an+3t-a,与an+1=4an-3n+1比较系数可得a= -1,t=0,所以数列{an-n}是首项为1,公比为4的等比数列,则an-n=4n-1,即an=4n-1+n.
问题B5若数列{an}满足an+1=3an+2n,a1=-1,求通项公式an.
解:应用待定系数法,令an+1+k2n+1=3(an+k2n),整理并比较系数可得an+1+2n+1=3(an+2n),
所以数列{an+2n}是首项1,公比为3的等比数列,则an+2n=3n-1,即an=3n-1-2n.
问题B6若数列{an}满足an+1=2an+2n,a1=1,求通项公式an.
若按照问题B5的方法,则求不出相应的k,所以其解法如下:
解:将an+1=2an+2n两边同时除以2n+1,得则
同理,对于问题B5,也可以将an+1=3an+2n两边同时除以2n或3n+1分别得到再加以求解.显然除以3n+1再用累加法求解相对简洁.
小结3:形如an+1=pan+dn(p≠1,d≠1),两边同时除以dn或pn+1后再进行求解.
在前面的例题中,an+1、an或an-1的次数均为1次,如果换成-1或2,又该如何解决?将问题B1中的an+1与an换成于是有下面的问题:
问题C1若数列{an}满足求通项公式an.
前面的问题,不管是整式型还是分式型,递推关系式均为一次,且只有an+1与an两项,如果递推关系式为二次或者有an+2、an+1与an三项,又该如何解决呢?
问题D1若数列{an}满足an+1=,a1=5,求通项公式an.
解:因为an+1=,所以两边同时取以5为底的对数得log5an+1=2log5an,则{log5an}是以1为首项,2为公比的等比数列,所以an=52n-1.
小结5:对于高次问题,我们主要的思想是降次,通过取对数或因式分解一般均能达到预期的效果.对于二阶常系数线性齐次递推数列,即形如an+2=pan+1+qan(其中p,q为常数,且q≠0),常用特征根法求解.课堂上只引导学生提出此类问题,课外兴趣小组再进行深入探讨与研究.课堂教学要让学生学会思考问题,知道知识的来龙去脉,能够提出问题.这比单纯地教会学生做几道题,死记一些解题技巧更有意义.
前几类问题中都只有an,但有些问题会出现an与Sn的关系,对于这类问题通常应用的是an=Sn-Sn-1(n≥2).
问题E1若数列{an}的前n项和为Sn,且满足Sn=2an+ n2-4n,求通项公式an.
解:由Sn=2an+n2-4n,可得a1=3,且Sn-1=2an-1+(n-1)2-4(n-1)(n≥2),
两式相减并整理可得an=2an-1-2(n-1)+3.
再由待定系数法得
an-2n+1=2[an-1-2(n-1)+1],
所以数列{an-2n+1}是首项为2,公比为2的等比数列,所以an=2n+2n-1,验证n=1也满足.所以an=2n+2n-1.
问题E2若数列{an}的前n项和为Sn,a1=1且满足an+1=
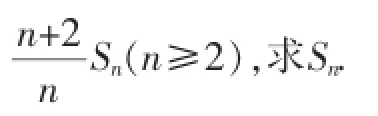

则Sn=n·2n-1(n≥2),当n=1时,S1=a1=1也满足等式,所以Sn=n·2n-1.
小结6:对于出现an与Sn的问题,要看题目的最终目标是什么.通过E1和E2不难发现,在E1中求an,则用升降足标法作差,即把Sn消掉;在E2中求Sn,则利用an+1=Sn+1-Sn把an+1消掉.所以这类题的主要思想是消元.
三、结束语
构建主义认为学习是学习者主动通过新旧知识间反复的、双向的相互作用,而建构自己的经验体系的过程.教学中,教师要在充分做好“双基”复习的基础上,选择一些基础性、启发性以及综合性的例题.不要脱离基础而搞所谓的拔高题,不过分地追求技巧教学.教师要引导学生从不同的角度对知识进行建构、分析、理解,形成良好的教学认知结构.
教学过程中教师不能无视学生已有的经验以及思维习惯,而要把学生现有的知识经验、思维能力作为新知识的出发点,通过启发与引导,让学生不断充实与完善自己的知识结构.我们要清楚地认识到教学过程不仅仅是知识、经验的传递,而是新旧知识间的转换以及结构重组处理的过程.所以在中小学的数学教学中我们要注意“数学情境与提出问题”.提出数学问题和解决数学问题是相互引发的,在解决数学问题和数学应用的过程中,已解决的问题和应用中的成果又可以作为提出新问题的数学情境,引发学生深一层次的探究与思考.
因此在上复习课时,教师不能以题海代复习,不能机械地罗列知识点以及例题.要注意教学策略,要选择好题,并发现它们之间的内在联系;并要做到例题之间过渡自然,通过设立数学情境与提出问题,促进学生在课堂上积极地去思考,尽量做到学有所思,学有所悟.通过学习体会到数学的自然与美,使学生能够举一反三、触类旁通,不断提高学习效率.同时通过课堂教学,培养学生的问题意识,不断提高学生提出问题与解决问题的能力,使学生形成对知识主动探究的态度,这样的教学方式对于培养、提高学生的思维能力、数学创新能力具有重要的现实意义.这些都充分体现新课程改革的核心思想.本文也正是基于这样的教学理念,选择了一个具体的课程内容(递推数列通项公式),做了一些尝试,并取得了一些实质性的教学效果.同时也希望我们的这些思考能引发更多教育研究者对数学教学策略改进与提高的关注和研究.
1.[美]波利亚.数学的发现[M].欧阳绛,译.北京:科学出版社,1982.
2.李邦河.数学概念的发展[J].数学通报(8),2009.
3.吕传汉,汪秉彝.再论中小学“数学情境与提出问题”的数学学习[J].数学教育学报,2002,11(4).

