善变——数学教学的艺术

苑建广（河北省晋州市实验中学）

善变
——数学教学的艺术

苑建广（河北省晋州市实验中学）

一题多思（变），有助于发展学生的思维品质.若深入挖掘，从横向、纵向、逆向、系统等多层次、多方向上进行思考、演变、拓展，必可深化教学内容，揭示问题实质，促进思维变通，发展创造能力，提高学习效率.几何问题变式可以探寻命题的可逆性，改变图形结构.代数问题的变式可以删减信息，调整信息给予方式，增加或改变设问方式.

变式教学；图形结构；信息给予方式

问题是数学的心脏，数学是思维的体操.通过解题发展学生的思维品质，是数学教学的中心问题.但是，过多、过密、盲目的解题，不仅不会促进学生思维能力的发展，反而容易窒息智慧，降低兴趣，产生疲劳感.只有举一反三、闻一知十、触类旁通的解题，才能激发学生深入思考，提升思维品质，而一题多思（变）无疑是事半功倍的.一题多思（变），有助于发展学生思维的深刻性、广阔性、灵活性、敏捷性、批判性，是激发创造力的有效途径.

一些习题，看似平凡，实却内涵丰富.若能深入挖掘，从横向、纵向、逆向、系统等多层次、多方向上进行思考、演变、拓展，必可深化教学内容，揭示问题实质，促进思维变通，发展创造能力，提高学习效率.本文以两道例题说明.

例1如图1，在△ABC中，点E在AC上，点F在BC上.过点C作CD⊥AB于点D，过点F作FG⊥AB于点G.连接DE，若∠1=∠3，试证明：DE∥BC.

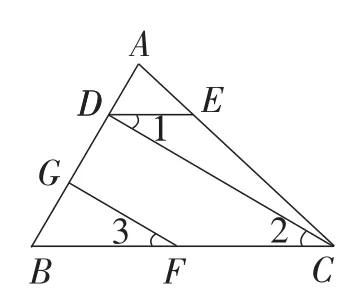
图1

这是在七年级学习“相交线与平行线”时最经典的一个例题，能通过综合运用平行线的性质与判定定理解题达到融会贯通相关知识内容的学习目的.

如何推陈出新，充分挖掘该题目的教学功能呢？在教研教学中，我们做到了以下几点.

首先，变换设问方式.

一方面，通过调换题设中的部分条件和结论的位置实现创新.

变式1：如图1，在△ABC中，点E在AC上，点F在BC上.过点C作CD⊥AB于点D，过点F作FG⊥AB于点G.连接DE，若DE∥BC，试证明：∠1=∠3.

变式2：如图1，在△ABC中，点E在AC上，点F在BC上，点G在AB上.过点C作CD⊥AB于点D.连接DE，FG，若DE∥BC，∠1=∠3，试证明：FG⊥AB.

另一方面，引例中的“CD⊥AB”和“FG⊥AB”只是为了引出“CD∥FG”这些线与线之间的特殊位置关系，可以变更为给出相关角的数量关系或赋以数据，从而实现创新.

变式3：如图1，在△ABC中，点D，G在AB上，点E在AC上，点F在BC上，连接DE，CD，FG，若∠CDB=∠FGB，∠1=∠3，试证明：DE∥BC.

变式4：如图1，在△ABC中，点D，G在AB上，点E在AC上，点F在BC上，连接DE，CD，FG，若∠CDB=∠FGB，DE∥BC，试证明：∠1=∠3.

变式5：如图1，在△ABC中，点D，G在AB上，点E在AC上，点F在BC上，连接DE，CD，FG，若∠1=∠3，DE∥BC，∠CDB=80°.求∠FGB的大小.

其次，变换图形结构.

在图1中，点F在BC上，有一定的随意性，能否将之调整到BC的延长线上或BC的反向延长线上？

变式6：如图2（或图3），在△ABC中，点E在AC上，点F在BC上.过点C作CD⊥AB于点D，过点F作FG⊥AB于点G.连接DE，若∠1=∠3，试证明：DE∥BC.

相应地，在图2（或图3）中还可以同变式1～5之题干般创新.

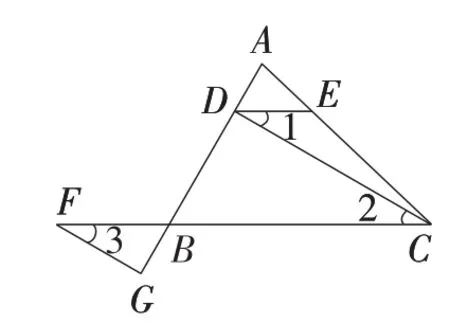
图2

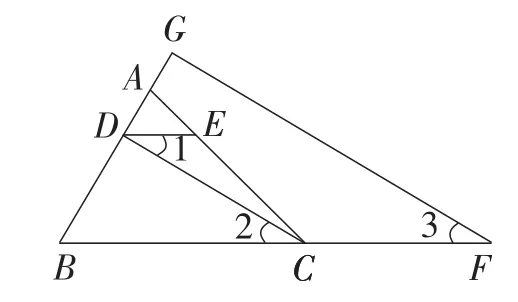
图3

在此基础上，能否把点D在AB上调整为点D在BA的延长线上或点D在AB的延长线上？

例如，保持点F在线段BC上，调整点D到BA的延长线上可以做如下变式.

变式7：如图4，在△ABC中，点D在BA的延长线上，点E在CA的延长线上，点F在BC上，点G在AB上，连接CD，DE，FG.若CD∥FG，∠EDC与∠GFB互补，试证明：DE∥BC.

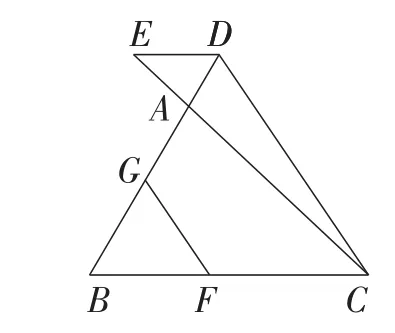
图4

相应地，在图4中还可以类似变式1～5之题干般调整，做出创新变式.当然，若考虑到DE∥BC也可以通过角的等量关系给予，每个图形还可以做出多种变式.类比以上方式可以找到更多变式情形.

如图5，可在图1的基础上，延长ED，FG交于点P，将线段BD向右平移，擦去图中的虚线，留下的实线图形.于是得到变式8.

变式8：如图5（实线部分），已知CD⊥D′B′于点N，PF⊥D′B′于点M.若∠1=∠2，试证明：PD′∥B′C.

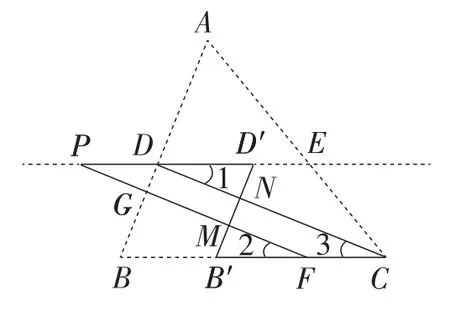
图5

类比以上其他变式情形，稍做调整，即可得到图5的其他更多变式情形.

【点评】如果能在课堂中生发出上述变化，对激发学生学习数学的兴趣，感悟数学的魅力，其效果是不言而喻的.如何在几何解题教学中推陈出新，充分开发题目的教学功能？几何图形的无非是由线以及线间所成的不同角度而构成的，而构成图形的线或角往往带有一定的随意性，通过变化某些线的位置或某些角度，往往可以在一定程度上改变图形的结构或是视觉上的熟悉程度，从而使题目变得新颖起来或增加了一定的难度.

由例1可见，若要通过调整线段来改变图形结构，往往先要确定调整哪一条线段（即调整对象），然后再决定如何调整它（即调整方法）.由于既可以调整点D的位置（有3个不同的位置类型），又可以调整点F的位置（也有3个不同的位置类型），总共组合出如上几种不同的图形类型.而图5的由来则要复杂一些.不过正是由于图5的出现才引发人们思考：之所以能变化出个多图形来，是因为这所有图形中均有两组平行线.

例2为了鼓励居民节约用水，某市自来水公司按如下方式对每户月水费进行计算：当用水量不超过10吨时，每吨的收费标准相同；当用水量超过10吨时，超出10吨的部分每吨收费标准也相同.表1是小明家1～4月份用水量和交费情况.

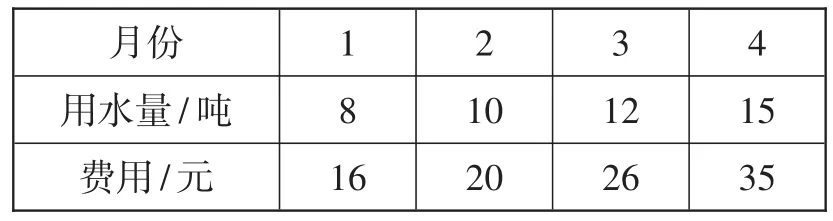
表1

请根据表1中提供的信息，回答以下问题.

（1）若小明家5月份用水量为20吨，则应缴水费为多少？

（2）若小明家6月份交纳水费29元，则小明家6月份用水的吨数为多少？

此例也是常见问题，如何推陈出新，充分挖掘该题目的教学功能呢？在教研教学中，我们做到了以下几点.

变式1：删去表格中的2月份和4月份信息，其他不变.

变式2：删去表格中的2月份和3月份信息，其他不变；

变式3：删去表格中的1月份和4月份信息，其他不变.

变式4：删去表格中的1月份和3月份信息，其他不变.

上述变式并没有改变题目的思维量，只是删掉了部分冗余信息.

变式5：删去表格中的1月份和2月份信息，其他不变.

这种变式已经不能通过简单读表得到月用水量在10吨以内部分的收费标准，而需要通过列方程（组）找出10吨以内部分和10吨以上部分的收费标准，进而完成题目解答.

变式6：将例2中的“当用水量不超过10吨时，每吨的收费标准相同；当用水量超过10吨时，超出10吨的部分每吨收费标准也相同”中的所有“10吨”改为“a吨”，其他不变.

这种变式提升了思维含量，题目考查的厚重度骤然提升.解决时需要结合表格对a分段讨论，布列方程（组），取舍各种情形，才能最终综合得到10吨以内部分和10吨以上部分的收费标准，进而完成题目解答.

变式7：将变式1～6中以表格形式给予信息的方式改变为以柱状图方式或折线图方式（图形不赘）给予信息，其他不变.

变式8：将变式1～6中增加新的设问，如找到月应缴水费与月用水量之间的函数关系式，画出图象等，其他不变.

【点评】通过此例可以发现有些代数题可以从以下角度进行变式.

（1）删减某些信息，题目是否可解？比如，删去表格中的3月份和4月份信息，其他不变，则题目不可解；而变式6相对于原题，不仅可解，难度和思维量上也增加不少，题目对思维品质考查的厚重度有所增强.正因为原题有冗余条件，才使善于变式教学的教师抓住了化腐朽为神奇的机会.

（2）调整信息给予方式.如变式7，把表格信息变为图形、图象信息，可以考查学生提取有用信息的能力，让表格、图象、图形等自然语言与式子一样说话.

（3）增加或改变设问方式.如变式8，要求学生建构函数关系式，画出图象，通过图象直观分析信息等.

两个变式教学的例题，一个在几何上变出精彩，一个在代数上变出花样，让数学的魅力彰显，让教学的艺术升华.仔细体味其中玄妙，必有益于未来数学教学效果之提升.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］王义堂，田保军，王硕旺.新课程理念与教学策略［M］.北京：中国言实出版社，2003.

2016—07—24

苑建广（1973—），男，中学高级教师，主要从事中学数学教育教学及中考命题研究.