冷热电联供机组性能曲线的在线拟合方法

刘洁，王恒涛，李义强，陈耀斌

（中国华电集团科学技术研究总院有限公司，北京　100070）

冷热电联供机组性能曲线的在线拟合方法

刘洁，王恒涛，李义强，陈耀斌

（中国华电集团科学技术研究总院有限公司，北京100070）

为了评估冷热电联供机组运行性能并进行实时优化，提出了一种用遗传算法对运行数据进行分段拟合的方法。遗传算法采用MATLAB现有的ga函数，利用最小二乘法评估拟合误差，分段点处利用约束保证连续、光滑。采用该方法对上海某分布式能源站余热锅炉的高压、低压蒸汽量和燃气轮机发电量的关系进行拟合，拟合结果表明，该方法能够实现自动分段拟合，拟合曲线能够准确反映数据趋势。

冷热电联供；性能曲线；遗传算法；分段拟合

0　引言

为解决环境污染问题，采用高效、清洁的能源供应方式已经成为目前能源的重点发展方向之一。在这样的背景下，以天然气为主要燃料的分布式冷热电联供机组受到国内外的广泛关注。冷热电联供机组利用烟气余热产生蒸汽、热水或冷水，能够同时提供发电、供热、制冷3种能量形式，实现了能源的梯级利用，因而具有较高的能源利用效率［1-3］。实际运行过程中，机组运行状态往往偏离设计工况，且机组的运行方式往往以保证安全和满足负荷为基本要求，而忽略了经济性和能源利用效率等，运行方式存在优化空间。为了及时评估机组性能，对机组运行方式进行优化调整［4-6］，往往需要基于当前机组运行数据进行性能曲线拟合，通过拟合结果，可对机组运行方式进行优化调整，提高机组运行效率和经济性，也可以直观地将当前机组的运行状况与设计值进行对比，发现机组潜在的问题。

在工程技术问题中经常涉及曲线拟合问题，现有的一些商业软件包含了便捷的曲线拟合工具，如MATLAB内置的lsqcurvefit，polyfit和曲线拟合工具箱cftool等。上述拟合工具基于给定的拟合数据和函数模型，利用最小二乘法［7-11］确定函数的待定参数。拟合函数模型以线性函数、多项式函数、指数函数和对数函数等为主。在给定数据关系较简单的情况下，一种函数模型可以较准确地逼近数据，采用现有的工具能够得到较好的拟合结果。然而对于电厂，运行数据与负荷密切相关，并且随着负荷的变化，数据具有显著的分段特点，采用一种函数往往不能充分描述数据变化趋势，需采用多种函数模型分段拟合的方式，数学约束条件较多，现有的拟合工具不适用。为此，本文提出了利用遗传算法进行曲线分段拟合的方法，在满足分段函数连续且可导的条件下，自动优化分段点位置并得到最优的拟合结果。

1　数学模型

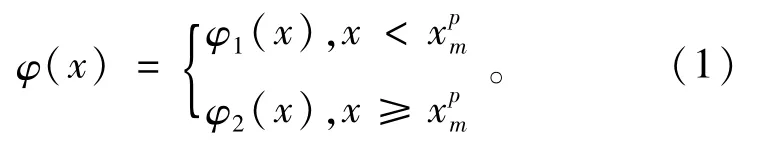
函数模型根据数据关系特点选取，在分段点处，为了保证函数连续且可导，需满足以下条件

在拟合函数模型确定的情况下，式（2）限定了函数待定参数需满足的条件。

2　拟合算法

2.1最小二乘法

最小二乘法是以令拟合函数与给定数据之间偏差的平方和最小为原则来确定拟合函数的方法，该方法可使给定的数据点最大限度地分布在拟合函数附近，既能反映数据的总体变化趋势，又不会使局部数据与拟合函数出现较大的偏离。对于式（1），最小二乘法为求解使下式L值最小的函数

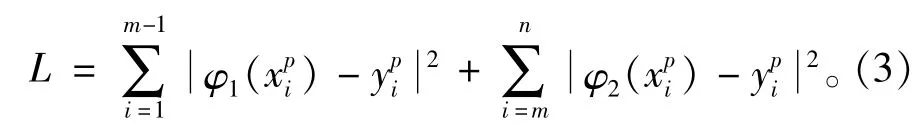
2.2遗传算法

遗传算法是一种常用的优化方法，通过模仿生物界的遗传进化过程寻找问题的最优解。优化时首先将优化问题的解通过编码转化为一一对应的染色体，然后随机生成初始种群，即一定个数的染色体。根据优化目标评估每一个体的适应度，从初始种群中选择个体作为新一代种群，其中适应度较优的个体被选择出来的概率较大，适应度较差的个体被选择的概率较小。在进化（即优化）过程中，染色体之间按照一定的概率进行交叉，生成新个体，这里交叉指染色体之间某些基因发生互换，互换的位置随机确定；染色体还可能发生变异，即染色体的基因根据一定的概率随机变为其他基因，通过变异也会产生新个体。交叉和变异保证了解的多样性，避免得到局部最优解。由于交叉、变异和选择操作，遗传至新一代个体适应度更优。随着遗传代数的增加，种群中最优个体的适应度不断优化直至趋于稳定，此时的最优个体就是问题的优化结果［12-13］。

在本文的曲线拟合问题中，拟合函数模型的待定参数为遗传算法的染色体，式（3）的值L则为遗传算法的适应度函数。在所有遗传算法的解中，使L取最小值对应的待定参数为遗传算法的最优解。

3　函数拟合的方法和步骤

利用MATLAB编写适应度函数，调用其内置的遗传算法函数ga并完成函数拟合的过程，其流程如图1所示，流程图中点划线框中为适应度函数L值的计算过程，虚线框中为ga函数实现的功能。函数拟合步骤如下。

图1　函数拟合流程

（1）令i=0。

（2）调用MATLAB内置遗传算法ga函数，调用时指定适应度函数、变量个数、变量取值上限和下限，此处的变量即为函数拟合时需确定的待定参数和分段点。

（3）ga函数给变量随机赋值。

（4）根据约束条件计算其余待定参数的值。

（5）所有待定参数和分段点确定后，判断拟合函数是否合理，合理则进入下一步，不合理则令适应度函数值L为无穷大。

（6）拟合函数的表达式确定后，根据式（3）计算L的值。

（7）判断是否达到MATLAB已设定的遗传算法最大代数：如果未达到，则重复步骤（3）及其后的过程；如果已达到，则计算当前拟合函数的R平方值，其计算公式为

式中：wi为权重系数，可取1为给定数据的平均值；R（0＜R＜1）代表拟合函数与给定数据的相关程度，越接近1说明拟合函数逼近程度越高。

（8）判断R平方值是否大于规定值（如0.95），如果满足则结束拟合过程，如果不满足则令i=i+1，重复步骤（2）以后的过程，直至R平方值大于规定值。

4　应用实例

上海某燃气分布式能源站是由2套燃气轮机、余热锅炉、汽轮机、发电机组成的机组，对外提供电力、蒸汽和空调冷（热）负荷。天然气燃烧后的烟气进入燃气轮机做功，做完功的烟气从燃气轮机排出后进入余热锅炉产生高压水蒸气和低压水蒸气。高压水蒸气可进入汽轮机做功或直接用作工业蒸汽。实际运行中，1台机组的燃气轮机发电量E对应的高压蒸汽流量qmh、低压蒸汽流量qml见表1，曲线关系如图2所示。

表1　燃气轮机发电量与高压蒸汽、低压蒸汽流量

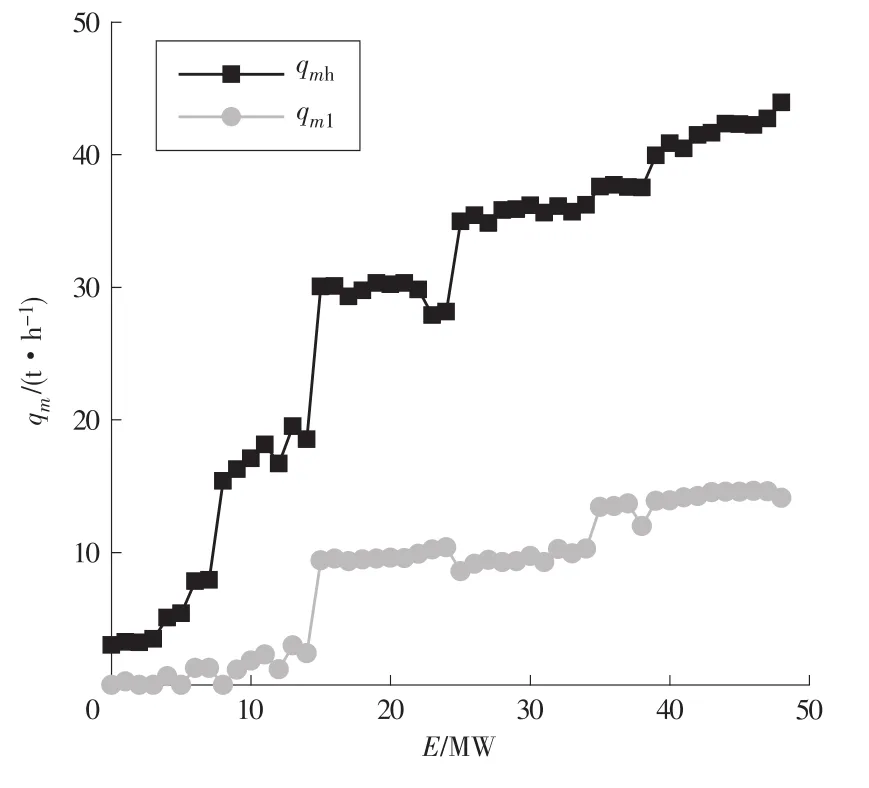
图2　燃气轮机发电量与高压蒸汽、低压蒸汽流量关系曲线

从实际运行数据可以看出：当燃气轮机发电功率低于5 MW或高于20 MW时，高压蒸汽流量随燃气轮机发电功率的增加较慢；当燃气轮机发电功率为5～20 MW时，高压蒸汽流量随燃气轮机发电功率的增加而迅速增加。低压蒸汽也有相似的变化特点：当燃气轮机发电功率低于14 MW或高于16 MW时，随着燃气轮机发电功率的增加，低压蒸汽流量增加较慢；当燃气轮机功率为14～16 MW时，低压蒸汽量迅速增加。该组数据呈现明显的分段特点，据此，将实际运行数据分两段进行拟合：燃气轮机发电功率较低时，采用二次函数；燃气轮机发电功率较高时，采用指数函数，函数模型为

式中：x为燃气轮机发电功率；φ为蒸汽流量。

当燃气轮机发电功率为0时，没有烟气通过余热锅炉，此时余热锅炉产生的高压（或低压）蒸汽量为0。由于测量误差的影响，实际蒸汽流量不为0（如图2所示），但在拟合曲线时强制令蒸汽流量为0，即φ（x=0）=a0=0。当燃气轮机发电功率较低时，蒸汽流量变化趋势表明二次函数应为下凸函数，二次项前系数应为正，即a2＞0；当燃气轮机发电功率较高时，蒸汽流量变化趋势表明指数函数应为上凸函数，指数项前系数为-1。分段点通过遗传算法求解，拟合函数中的待定参数个数为6。由式（2）的约束条件，待定参数个数减少为4。此外，可利用现有拟合工具对运行数据分组进行初步拟合，评估待定参数的数量级，缩小待定参数的取值范围，提高遗传算法的求解效率。

根据本文拟合方法得到的结果如图3所示，其中高压蒸汽流量R平方值设为0.97，低压蒸汽流量R平方值设为0.91。从图中可以看出，拟合函数在低负荷和高负荷段能够很好地逼近运行数据，由于中间负荷区域蒸汽量变化较快，拟合函数存在一定误差，但整体能够反映负荷快速变化的趋势。此外，由于燃气轮机一般以高负荷运行，高负荷段拟合的准确性具有更重要的意义。

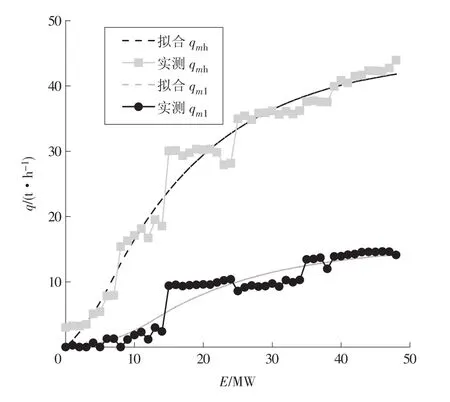
图3　拟合结果与实测数据对比

高压蒸汽流量与燃气轮机发电功率的拟合曲线方程为

低压蒸汽流量与燃气轮机发电功率的拟合曲线方程为

5　结束语

与现有拟合工具相比，本文的优化方法能够进行自动分段拟合，并能保证拟合结果达到预设的精度。由于遗传算法可以自行编写或利用现有的函数，该方法可以嵌入机组运行优化软件中，进行在线拟合、设备评估和实时优化。对于复杂的数据，该方法也能够实现3段或以上分段函数的拟合。

［1］吴波.分布式能源冷热电多联产系统能效分析与可比性方法研究［D］.北京：北京科技大学，2015.

［2］李佩，王健，何石泉，等.天然气分布式能源系统的能源综合利用效率计算［J］.暖通空调，2014，44（10）：13-17.

［3］陈强，纪星星，李义强，等.余热利用冷电联供系统热力性能分析［J］.热力发电，2015，44（9）：32-42.

［4］许伟强.某分布式能源系统中冷热电三联产控制优化分析［J］.发电与空调，2014，35（158）：1-5.

［5］李义强，王恒涛，陈耀斌，等.一种分布式能源系统的运行优化控制方法及系统：CN104571068［P］.2015-04-29.

［6］陈耀斌，孔飞，李义强，等.燃气分布式发电系统的硬件在环实时仿真系统：CN204302786U［P］.2015-04-29.

［7］谭晓慧，余伟，沈梦芬，等.土-水特征曲线的试验研究及曲线拟合［J］.岩土力学，2013，34（S2）：51-56.

［8］陈岚峰，杨静瑜，崔崧，等.基于MATLAB的最小二乘曲线拟合仿真研究［J］.沈阳师范大学学报（自然科学版），2014，32（1）：75-79.

［9］李蓓蕾.多次自适应最小二乘曲线拟合方法及其应用［D］.荆州：长江大学，2014.

［10］侯超钧，曾艳姗，吴东庆，等.全局连续的分段最小二乘曲线拟合方法［J］.重庆师范大学学报（自然科学版），2011，28（6）：44-48.

［11］刘霞，王运锋.基于最小二乘法的自动分段多项式曲线拟合方法研究［J］.科学技术与工程，2014，14（3）：55-58.

［12］陈国良，王煦法，庄镇泉，等.遗传算法及其应用［M］.北京：人民邮电出版社，1996.

［13］李敏强.遗传算法的基本理论与应用［M］.北京：科学出版社，2002.

（本文责编：刘芳）

TM 611

A

1674-1951（2016）08-0012-04

2016-05-06；

2016-07-06

刘洁（1988—），女，北京人，助理工程师，从事分布式能源的研究（E-mail：jie-liu＠chdi.ac.cn）。