一道预赛试题的简证及推广*

●李 歆

(武功县教育局教研室 陕西武功 712200)



一道预赛试题的简证及推广*

●李 歆

(武功县教育局教研室 陕西武功 712200)

用均值不等式和柯西不等式联合证明竞赛不等式，既能便于学生理解，又能体现这2个重要不等式的综合应用价值.

预赛题；不等式；推广

例1 设a,b,c为正实数,且满足abc=1.对任意n≥2,证明:

(1)

(2016年全国高中数学联赛陕西赛区预赛第二试第5题)

文献[1]利用切比雪夫不等式和幂平均不等式给出了一种证明,但多数学生对切比雪夫不等式和幂平均不等式比较陌生,因此对此证法难以理解.笔者利用一般学生都熟悉的均值不等式和柯西不等式给出一种简单的证明,同时将这道预赛试题加以推广.

证明 不等式(1)等价于

(2)

由n元均值不等式,得

则不等式(2)可转化为

(3)

由柯西不等式,得

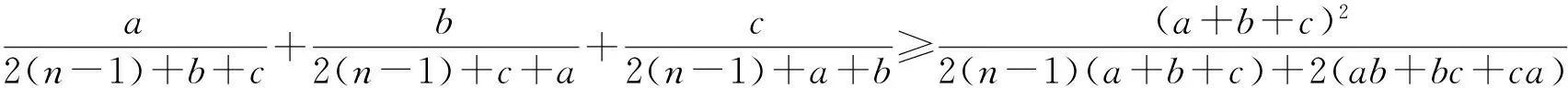
(4)

式(4)等价于n(a+b+c)2≥3(n-1)(a+b+c)+3(ab+bc+ca).

(5)

由

(a+b+c)2≥3(ab+bc+ca),

可知式(5)成立,进而式(4)、式(3)、式(2)成立,从而不等式(1)成立.

推广1 设a,b,c为正实数,且满足abc=1.对任意n≥2,λ>0,证明:

(6)

证明 不等式(6)等价于

(7)

由n元均值不等式,得

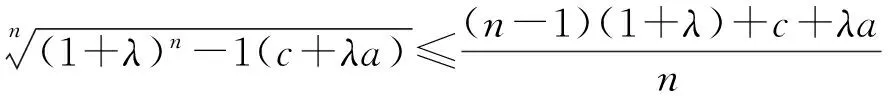
则不等式(7)可转化为

(8)

由柯西不等式,得

则不等式(8)可转化为

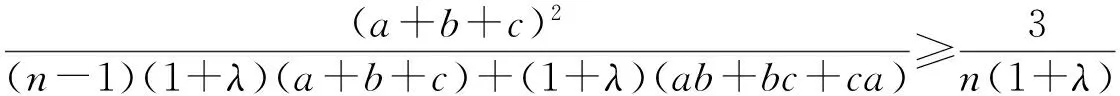
(9)

式(9)等价于n(a+b+c)2≥3(n-1)(a+b+c)+3(ab+bc+ca).

(10)

由

(a+b+c)2≥3(ab+bc+ca),

可知式(10)成立,进而可知式(9)、式(8)、式(7)成立,从而不等式(6)成立.

推广2 设a,b,c为正实数,且满足abc=1.对任意n≥2,λ≥0,证明:

(11)

证明 不等式(11)等价于

(12)

由n元均值不等式,得

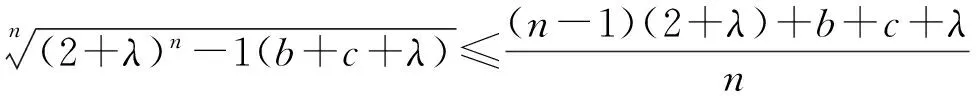
则不等式(12)可转化为

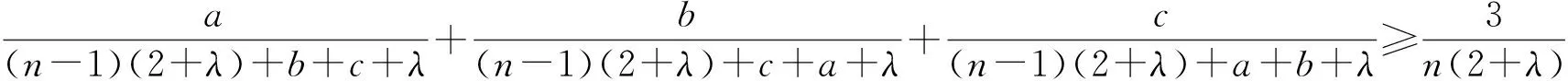
(13)

由柯西不等式,得

则不等式(13)可转化为

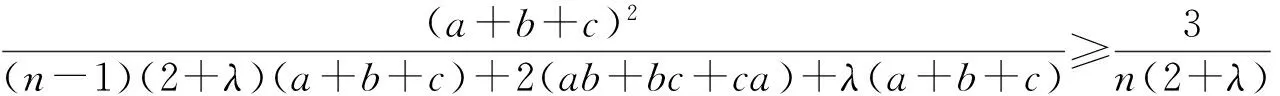
(14)

式(14)等价于n(2+λ)(a+b+c)2≥3(n-1)(2+λ)(a+b+c)+6(ab+bc+ca)+3λ(a+b+c).

(15)

由

(n-1)(2+λ)(a+b+c)2≥3(n-1)(2+λ)(a+b+c),

2(a+b+c)2≥6(ab+bc+ca),λ(a+b+c)2≥3λ(a+b+c),

可知式(15)成立,进而可知式(14)、式(13)、式(12)成立,从而不等式(11)成立.

类似可以证明:

推广3 设a,b,c为正实数,且满足abc=1.对任意n≥2,λ1>0,λ2≥0,证明:

[1] 陕西省数学竞赛委员会.2016年全国高中数学联赛陕西赛区预赛试题及参考答案[J].中学数学教学参考:上旬,2016(5):58.

�2016-07-20；

2016-09-12

李 歆(1962-)，男，陕西武功人，陕西省特级教师.研究方向：数学教育.

O122.3

A

1003-6407(2016)11-48-03