萤火虫算法收敛分析*

陆克中，孙　俊

1.池州学院 计算机科学系，安徽 池州 247100

2.中国科学技术大学 计算机科学与技术学院，合肥 230026

3.江南大学 物联网工程学院，江苏 无锡 214021

萤火虫算法收敛分析*

陆克中1,2+，孙俊3

1.池州学院 计算机科学系，安徽 池州 247100

2.中国科学技术大学 计算机科学与技术学院，合肥 230026

3.江南大学 物联网工程学院，江苏 无锡 214021

LU Kezhong,SUN Jun.Convergence analysis of firefly algorithm.Journal of Frontiers of Computer Science and Technology,2016,10(2)：293-300.

为了系统地分析萤火虫算法（firefly algorithm,FA），首先对FA算法的收敛过程进行了分析，得出FA算法收敛的两个一般条件：随机扰动项的数学期望等于0；最大吸引度β0∈(0,2)，通常取β0∈(0,1]，并且β0越大，算法收敛速度越快。接着根据随机算法的收敛准则，证明了FA算法不具有全局收敛特性。然后应用数学归纳法，结合夹逼定理及反证法，从理论上证明了FA算法收敛于群体最优解，是一个局部收敛算法。最后对不同条件下的FA算法收敛性进行了仿真，实验结果与理论结果一致，佐证了理论分析的正确性。

萤火虫算法；收敛分析；局部收敛

1　引言

2008年，剑桥大学的Yang[1]受萤火虫利用自身荧光传递信息这种群体行为的启发，提出了一种新颖的群智能优化算法——萤火虫算法（firefly algorithm，FA）。相比较而言，FA算法具有结构简单，调节参数少，收敛速度快，易于操作实现等特点[2]，自提出以来，已经在图形图像处理[3]、聚类分析[4]、机械设计[5]、任务调度[6]、证券投资[7]、软件测试[8]等领域得到了应用，并取得了较好的效果。

当前，国内外学者对FA算法的研究越来越多，但主要集中在算法自身的改进，以及算法在不同领域的应用上，还缺乏对算法进行系统的理论分析，特别是算法的收敛条件与收敛特性方面。现有的一些对FA算法的分析均是基于实验方法进行的，如文献[9]通过对FA算法的参数进行分析，提出了基于距离的光吸系数等多种参数调节方法，以提高算法的自适应能力；文献[10]基于5个标准测试函数，分析了算法的参数选择、群体规模以及目标函数对算法性能的影响，并指出难以找到对所有问题均有效的统一参数调节方法；文献[11]通过实验指出，FA算法的收敛效果与萤火虫群体规模以及算法的迭代次数直接成正比。文献[12]通过对一些标准测试函数的仿真，指出FA算法存有早熟收敛，后期收敛速度慢，求解精度较低等缺点；文献[13]在对算法参数进行分析的基础上，引入混沌策略，调节算法的参数，增强算法的全局搜索能力；还有一些在分析FA算法性能基础上，引入其他算法，取长补短，构成混合优化算法[14-15]。

由于FA算法还缺乏系统性分析，特别是收敛性方面的理论证明还未见报道，这在一定程度上制约了算法的研究与发展。为此，本文在对FA算法进行系统分析的基础上，给出了算法收敛性分析的理论证明，并应用实验方法对算法的不同收敛情况进行了仿真分析。

2　基本FA算法

Yang模拟自然界萤火虫发光模式与信息交换行为，提出了FA算法。其中荧光亮度和吸引度是FA算法中两个关键因素。假设萤火虫的群体规模为m，问题空间为d维，第i只萤火虫在d维空间中的位置表示为xi=()

xi1,xi2,…,xid。

定义1荧光亮度：

式中，I0为萤火虫的最大荧光亮度，即为r=0处的自身荧光亮度，取决于需要寻优的目标函数值，一般用式（2）表示，f(x)越好则I0就越高；γ为光强吸收因子，表示荧光亮度受传播距离与传播媒介的影响而变化的特性，理论上γ∝[0,∞]，但在实际应用中，γ=O(1)，常取[0.01,100]之间的某一常数；r表示两只萤火虫之间的空间距离，一般用式（3）的欧式距离表示。

其中，f为待优化函数；x为某一萤火虫的空间位置。

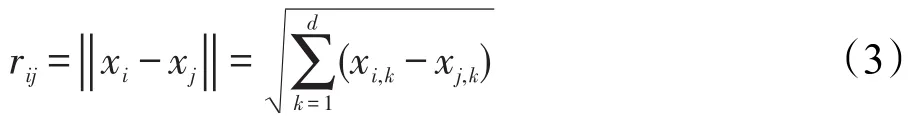
定义2吸引度：

式中，β0为最大吸引度，即光源（r=0处）的吸引度，通常设定为1；γ和r的意义同定义1。

定义3位置更新公式：

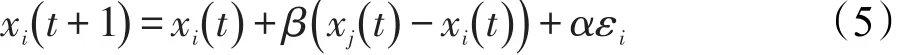
上式表示的是萤火虫i受萤火虫j的吸引，而发生位置改变。其中，t为迭代次数；xi与xj分别表示萤火虫i与j的空间位置；β表示萤火虫j对萤火虫i的相对吸引度；α为步长因子，α∝[0,1]；εi是一个服从高斯分布或均匀分布的随机向量，其简化形式为rand()-1/2，rand()为[0,1]内服从均匀分布的随机数。

FA算法流程描述如下：

步骤1设置参数γ，β0和最大迭代次数MaxGen；

步骤2初始化萤火虫群体xi(i=1,2,…,n) ，并计算xi的目标函数 f(xi) ，将其定义为荧光亮度Ii；

步骤3由式（3）计算萤火虫xi、xj之间的距离rij；

步骤4由式（4）计算萤火虫xj对xi的吸引度β；

步骤5由式（5）更新萤火虫xi位置；

步骤6若达到最大迭代次数，则停止，否则搜索循环次数加1，转步骤3。

3　FA算法收敛分析

对于式（5），可分为用于算法收敛的Part1部分和用于个体局部扰动的Part2部分：

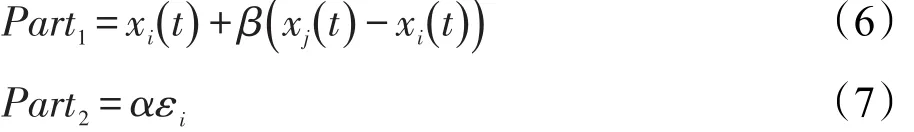
3.1FA算法收敛条件分析

对于Part2部分，个体在不断迭代过程中，αεi将不断地进行累加操作，即∑Part2=αε1+αε2+…+αεt。

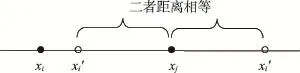
Fig.1　Two kinds of distance between fireflies图1　萤火虫个体两种距离关系

从图1可明显看出，因萤火虫个体在xi与xj之间移动，所以取左边部分xi′为xi的更新位置，即要求0＜β≤1，也即要求：

由上可得：若FA收敛，则0＜β0＜2，一般取0＜β0≤1。□

Fig.2　Trajectories of fireflies图2　萤火虫个体运动轨迹

3.2FA算法全局收敛性分析

文献[16]在对随机优化算法进行深入研究的基础上，给出了随机算法的求最小问题的收敛准则。对于优化问题＜S,f＞，随机优化算法A在第k次迭代的结果为xk，下一次迭代的结果为xk+1=A() xk,ξ，其中S是可行解空间，f为目标函数，ξ为算法A迭代过程中得到的解。

3.3FA算法局部收敛性分析

由定理4，FA算法不具有全局收敛特性，下面考察FA算法的局部收敛情况。FA算法的局部收敛性分析是在满足定理1与定理2的条件下进行的。

定理5次优解收敛于群体最优解。

推论2 FA算法是一个局部收敛算法。

证明 由定理7，FA算法收敛于群体最优解，由于群体最优解不一定是全局最优解，其解与群体的位置有关。若群体散落在全局最优解附近，其群体最优解往往就是全局最优解，若群体散落在局部极值点附近，其群体最优解往往就是局部最优解，所以FA算法是一个局部收敛算法。□

4　实验分析

为了直观地考察FA算法的收敛情况，这里使用实验的方法对不同条件下的算法进行了仿真，仿真所使用的函数为式（48）的四峰函数，此函数存在4个极大值，坐标分别是(0,-4)、(0,0)、(-4,4)、(4,4)，对应的极值分别为2、2、1、1。

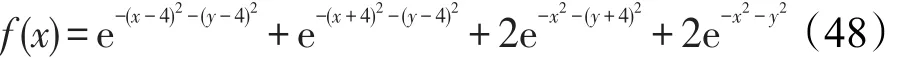
依据前面的理论分析，设定如下7个仿真条件，用以考察FA算法在不同参数设置下的收敛情况。其中共同的参数有α=0.2，γ=0.1，群体规模m=12，最大迭代次数MaxGen=50。

（1）β0=0.1，ε=rand()-1/2，range=[-5,5]；

（2）β0=1，ε=rand()-1/2，range=[-5,5]；

（3）β0=1.1，ε=rand()-1/2，range=[-5,5]；

（4）β0=1.9，ε=rand()-1/2，range=[-5,5]；

（5）β0=10，ε=rand()-1/2，range=[-5,5]；

（6）β0=1，ε=rand()-1/2，range=[0,5]；

（7）β0=1，ε=rand()，range=[-5,5]。

（1）～（5）这5种参数设置，用于考察β0在不同范围内对算法收敛情况的影响；情况（6）用于考察算法的全局收敛能力；情况（7）用于考察E(ε)≠0时，算法的收敛情况。情况（7）的实验结果见图3。

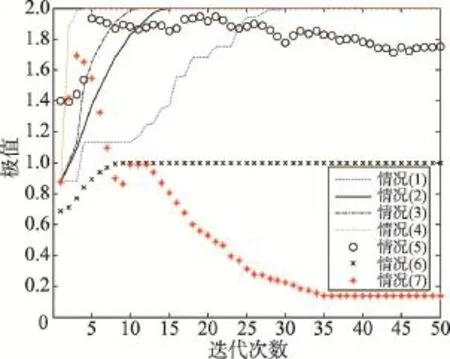
Fig.3　Convergence curves under different parameters图3　不同参数下的收敛曲线

参数设置的（1）～（4）情况中0＜β0＜2，从图3中可明显看出，FA算法收敛到全局最优解2，与定理2一致。其中，β0=1时明显比 β0=0.1时收敛速率要快，这是由于当0＜β0≤1时，由式（11）可知，β0越大，1-β0就越小，则新的萤火虫个体就更靠近较优个体，故而收敛越快，反之，收敛越慢。情况（3）与（4）满足1≤β0＜2，是萤火虫个体在背离较优个体一侧运动的情况，β0越大，则||1-β0就越小，由式（12）知，算法收敛越快，反之，收敛越慢，图3也印证了这个结论。当 β0=5时，对应情况（5），此时 β0不满足定理2中的0＜β0＜2条件，从而萤火虫个体不能向较优个体靠近，而是远离较优个体，缺失了群体启发信息，导致算法发散。从图3中可以看出，情况（5）的曲线出现了震荡，特别是在迭代后期，算法还偏离了极值点而呈发散态。当算法的初始解在局部极值点附近时，如情况（6），初始解范围是[0,5]，这样初始解已不在全局最优解附近，而是在局部极值点（4,4）附近，算法经多次运行测试，即使MaxGen=10 000，其结果均呈现如图3所示情况，收敛于局部极值点1，反映了FA算法的局部收敛特性，这与定理4关于FA算法不具有全局收敛性一致，也印证了推论2：FA算法是一个局部收敛算法。情况（7）考察的是E(ε)≠0时算法的收敛情况，从图3中可以看出，由于ε=rand()，致使E(ε)≠0，这样在迭代过程中，因累积效应，使得最终的萤火虫群体没有像情况（2）那样，聚集在全局最优解2上，而是随着迭代的进行，逐渐偏离最优解，呈现明显发散状态，其情况与定理1的结论一致。

5　结束语

本文从FA算法收敛过程入手，对FA算法的收敛条件与收敛性进行了分析与论证，得出算法收敛的两个条件：（1）随机扰动项的数学期望E(ε)=0；（2）最大吸引度 β0限制在0＜β0＜2，且一般取0＜β0≤1，并推论出萤火虫个体以折线形式向最优个体靠近的结论。接着利用随机算法的收敛准则，证明了FA算法不具有全局收敛特性。然后在以上基础上，结合夹逼定理，应用数学归纳法，从理论上证明了FA算法收敛于群体最优解，以及局部收敛的结论。最后应用实验方法，对不同条件下的FA算法收敛性进行了仿真，仿真结果与理论结果保持一致，进一步佐证了理论分析结论的正确性。今后，将进一步改进FA算法，特别是对于FA算法的全局收敛能力方面，以提升FA算法的优化效果。

References:

[1]Yang Xinshe.Nature-inspired metaheuristic algorithms[M]. Beckington:Luniver Press,2008:81-96.

[2]Yang Xinshe.Firefly algorithms for multimodal optimization[C]//LNCS 5792:Proceedings of the 5th International Conference on Stochastic Algorithms:Foundation and Applications,Sapporo,Japan,Oct 26-28,2009.Berlin,Heidelberg:Springer,2009:169-178.

[3]Horng M H,Liou R J.Multilevel minimum cross entropy threshold selection based on the firefly algorithm[J].Expert Systems withApplications,2011,38(12):14805-14811.

[4]Senthilnath J,Omkar S N,Mani V.Clustering using firefly algorithm:performance study[J].Swarm and Evolutionary Computation,2011,1(3):164-171.

[5]Gandomi A H,Yang Xinshe,Alavi A H.Mixed variable structural optimization using firefly algorithm[J].Computers and Structures,2011,89(23/24):2325-2336.

[6]Yang Xinshe,Hosseini S S S,Gandomi A H.Firefly algorithm for solving non-convex economic dispatch problems with valve loading effect[J].Applied Soft Computing,2012, 12(3):1180-1186.

[7]Kazema A,Sharifia E,Hussain F K,et al.Support vector regression with chaos-based firefly algorithm for stock market price forecasting[J].Applied Soft Computing,2013, 13(2):947-958.

[8]Srivatsava P R,Mallikarjun B,Yang Xinshe.Optimal test sequence generation using firefly algorithm[J].Swarm and Evolutionary Computation,2013,8:44-53.

[9]Cheung N J,Ding Xueming,Shen Hongbin.Adaptive firefly algorithm:parameter analysis and its application[J]. PLoS ONE,2014,9(11):1-12.

[10]Arora S,Singh S.The firefly optimization algorithm:convergence analysis and parameter selection[J].International Journal of ComputerApplications,2013,69(3):48-52.

[11]Yang Xinshe.Firefly algorithm stochastic test functions and design optimization[J].International Journal of Bio-Inspired Computation,2010,2(2):78-84.

[12]Łukasik S,Żak S.Firefly algorithm for continuous constrained optimization tasks[C]//LNCS 5796:Proceedings of the 1st International Conference on Computational Collective Intelligence,Wroclaw,Poland,Oct 5-7,2009.Berlin, Heidelberg:Springer,2009:97-106.

[13]Gandomi A H,Yang Xinshe,Talatahari S,et al.Firefly algorithm with chaos[J].Communications in Nonlinear Science and Numerical Simulation,2013,18(1):89-98.

[14]Yang Xinshe.Firefly algorithm,Levy flights and global optimization[M]//Research and Development in Intelligent Systems XXVI.London,UK:Springer,2010:209-218.

[15]Yu Shuhao,Su Shoubao.Research and application of chaotic glowworm swarm optimization algorithm[J].Journal of Frontiers of Computer Science and Technology,2014,8(3): 352-358.

[16]Solis F,Wets R.Minimization by random search techniques[J]. Mathematics of Operations Research,1981,6(1):19-30.

附中文参考文献：

[15]郁书好,苏守宝.混沌萤火虫优化算法的研究及应用[J].计算机科学与探索,2014,8(3):352-358.

陆克中（1976—），男，安徽枞阳人，2005年于江南大学获得硕士学位，现为池州学院副教授，中国科学技术大学访问学者，主要研究领域为智能计算，生物信息学等。发表学术论文16篇，主持安徽省自然科学研究项目2项。

孙俊（1971—），男，江苏无锡人，2009年于江南大学获得博士学位，现为江南大学副教授、硕士生导师，主要研究领域为进化计算，人工智能等。发表学术论文30余篇，主持国家自然科学基金项目1项。

ConvergenceAnalysis of FireflyAlgorithm*

LU Kezhong1,2+,SUN Jun3
1.Department of Computer Science,Chizhou University,Chizhou,Anhui 247100,China
2.School of Computer Science and Technology,University of Science and Technology of China,Hefei 230026,China
3.School of Internet of Things Engineering,Jiangnan University,Wuxi,Jiangsu 214021,China
+Corresponding author:E-mail:luke76@163.com

The purpose of this paper is to analyze the firefly algorithm(FA)systematically.Firstly,two general convergence conditions are obtained by analyzing the convergence process of FA.One is that mathematical expectation of random disturbance term is equal to 0,the other is that maximum attractiveness valueβ0belongs to(0,2),and usually belongs to(0,1],and the moreβ0value,the faster convergence speed.Nextly,according to the criterion of convergence of random algorithm,this paper proves that the FA is not a globally convergent algorithm.Then,this paper theoretically proves that the FA converges to the local optimal solution by using mathematical induction,sandwich theorem and apagoge.Finally,the convergence processes of FA under different conditions are simulated.The experimental results agree well with the theoretical results and prove the correctness of the theory analysis.

firefly algorithm;convergence analysis;local convergence

2015-04,Accepted 2015-06.

LU Kezhong was born in 1976.He the M.S.degree in computer application from Jiangnan University in 2005.Now he is an associate professor at Chizhou University.His research interests include intelligent computing and bioinformatics,etc.

SUN Jun was born in 1971.He the Ph.D.degree in control theory and control engineering from Jiangnan University in 2009.Now he is an associate professor and M.S.supervisor at Jiangnan University.His research interests include evolutionary computing and artificial intelligence,etc.

10.3778/j.issn.1673-9418.1504051

*The National Natural Science Foundation of China under Grant No.61170119(国家自然科学基金);the Natural Science Foundation ofAnhui Province under Grant No.KJ2016Z264(安徽省自然科学研究项目).

CNKI网络优先出版：2015-06-29,http://www.cnki.net/kcms/detail/11.5602.TP.20150629.1544.001.html

A

TP301.6