谈高考中二项式定理的题型

北京师范大学大兴附属中学 董 丽

谈高考中二项式定理的题型

北京师范大学大兴附属中学 董 丽

二项式定理是高考常考的题型之一,利用一些特殊的方法可以解决一些问题，本文列举了几种常用的方法.

二项式定理 通项 高中数学

二项式定理是高中数学中一个重要的知识点，涉及二项式定理应用的题型很多，解法灵活且比较难掌握.二项式定理既是排列组合的直接应用，又与概率理论中的三大概率分布之一的二项分布有着密切联系.二项式定理在每年的高考中基本上都有考到，题型多为选择题、填空题，偶尔也会有大题出现.本文将给出二项式定理在高考中的六种常考题型.

类型一：求展开式中的常数项

A.80 B.-80 C.40 D.-40

【答案】C

A.-1320 B.1320

C．-220 D．220

【答案】C

评注：解决这类题目要抓住通项公式进行求解.

类型二：求展开式中某一指定项的系数

例3（2015高考福建，理11）（x+2）5的展开式中，x2的系数等于___.（用数字作答）

【答案】80

【解析】本题考查二项式定理的特定项问题，根据二项展开式的通项和所求项的联系解题，（x+2）5的展开式中x2项为=80 x2，所以 x2的系数等于 80.

例4（2015高考北京，理9）在（2+x）5的展开式中，x3的系数为____.（用数字作答）

【答案】40

本题考查二项式定理，利用通项公式求出指定项的系数，本题属于基础题，要求正确使用通项公式准确计算指定项的系数.

类型三：求二项式中所含参数的值

例5（2015高考新课标2，理15）（a+ x）（1+x）4的展开式中x的奇数次幂项的系数之和为32，则a=_________．

【答案】3

【解析】由已知得（1+x）4=1+4x+6x2+ 4x3+x4，故（a+x）（1+x）4的展开式中x的奇数次幂项分别为4ax，4ax3，x，6x3，x5，其系数之和为 4a+4a+1+6+1=32，解得a=3．

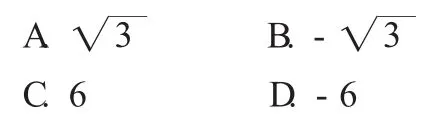
【答案】D

本题主要考查了二项式定理的运用，属于容易题，只要掌握（a+b）n的二项展开式的通项第r+1项为即可建立关于a的方程，从而求解.

评注：利用展开式的通项公式，根据题意建立方程或不等式，求出参数的值.

【答案】-2.

类型四：求二项式的幂指数

例8（2015高考陕西，理4）二项式（x+1）n（n∈N+）的展开式中x2的系数为15，则n=（ ）

A.7 B.6 C.5 D.4

【答案】B

【解析】二项式（x+1）n的展开式的通项是，令r=2得x2的系数是C2n，因为x2的系数为15，所以，即n2-n-30=0，解得：n=6或n=-5，因为n∈N+，所以n=6，故选B．

A.4 B.5 C.6 D.7

【答案】B

类型五：求展开式中某些项系数的和

例10（2007高考江西，文5）设（x2+1）（2x+1）9=a0+a1（x+2）+a2（x+2）2+…+a11（x+2）11，则a0+a1+a2+…+a11的值为（ ）A.-2 B.-1 C.1 D.2

【答案】A

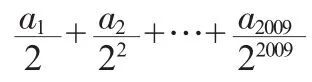
A.2 B.0 C.-1 D.-2

【答案】C

评注：此类题用赋值法能较好地解答.

类型六：利用二项式定理解整除问题

A.x=4，n=3 B.x=4，n=4

C.x=5，n=4 D.x=6，n=5

【答案】C

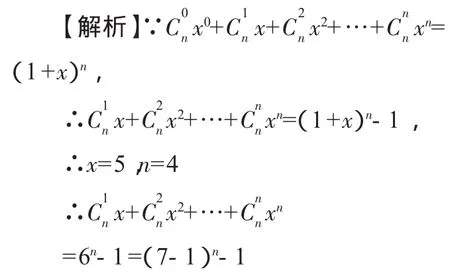
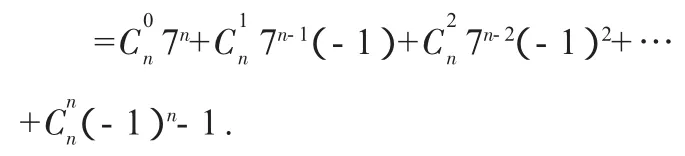
以上介绍了近年来高考对二项式定理问题考查的六种类型，掌握好上述常规的二项式定理题目的解题方法，无疑对我们后续知识的学习，以及将来的高考吃了一颗制胜的定心丸.

[1]人教A版教材选修2-3

[2]历年高考真题