基于DSP+FPGA的直流伺服系统电流环
陈 健 王伟国 张振东 姜润强
(中国科学院长春光学精密机械与物理研究所,长春 130033)
基于DSP+FPGA的直流伺服系统电流环
陈 健 王伟国 张振东 姜润强
(中国科学院长春光学精密机械与物理研究所,长春 130033)
在传统的速度环位置环双闭环控制系统中,小惯量直流力矩电机伺服系统因受力矩波动影响,其慢速运行精度很难有较大提高。为此,提出通过增加电流环内环的方法,并给出了相应的高效经济的实现方法。首先建立直流电机的数学模型,列举产生力矩波动的原因,从理论上分析电流环抑制力矩波动和增加速度环低频增益的作用,然后针对电流环高速、大数据量和实时性强的特点,设计基于DSP+FPGA的新型伺服控制器和功率级驱动模块,给出硬件结构和软件流程。实验结果:电流闭环带宽300Hz,能够有效抑制力矩波动。可适用于光电经纬仪,使其跟踪精度大为提高。
电流环 力矩干扰 电流环内环 直流电机数学模型 DSP+FPGA
由于直流力矩电机具有响应时间快、过载能力强和力矩系数大的特点,所以在光电伺服系统中得到了日益广泛的应用。力矩电机与负载直接耦合的方式可以增加系统带宽并加快响应速度,但也会把电机的力矩波动传递到系统中,对低速平稳性的影响尤为突出。力矩电机的力矩波动主要是由齿槽效应、摩擦力矩、电磁场相互作用和导体换向造成的。其中由电磁场相互作用产生的力矩波动与电机内部磁场分布有关,是组成力矩波动的主要因素,齿槽效应与电机内部导体分布有关,磁路不对称或极弧系数大小的不同都会引起力矩波动,换向阀换向时会引起电火花,导致电枢电流变化,从而导致力矩波动[1]。
在经典的速度位置控制结构中,往往忽略力矩波动影响,将速度回路控制对象简化为两个一阶惯性环节和一个振荡环节串联,其中两个一阶惯性环节代表力矩电机的机械特性和电气特性,振荡环节代表系统的谐振特性。然后进行控制器设计,常采用PID及超前滞后等方法。经典控制方法易于工程实现,但对扰动量抑制考虑不足,导致在实际应用中系统易受扰动干扰,尤其是力矩波动对系统的干扰,很难满足高精度低速伺服系统对精度和平稳性的要求[2]。为此,笔者提出通过增加电流环内环的方法来抑制力矩波动。
直流伺服力矩电机在额定励磁且电枢电流连续的情况下,电枢回路电压的动态平衡方程如下:
Ud0=E+IaR+L(dIa/dt)
(1)
E=Cen
(2)
式中Ce——反电动势系数;
E——电枢反电动势;
Ia——电枢电流;
L——电枢电感;
n——转子转速;
R——电枢电阻;
Ud0——电枢电压。
将式(1)、(2)进行拉普拉斯变换可得:
Ud0(s)-E(s)=R(Ia(s)+TasIa(s))
(3)
其中Ta是电机的电气时间常数,Ta=L/R。
化简式(3)可得:
Ia(s)/(Ud0(s)-E(s))=1/(R(Tas+1))
(4)
电机输出转矩与电枢电流成正比,转矩动态平衡方程为:
Tem-TL=J(dn/dt)
(5)
式(5)中,Tem为电机输出转矩,它与电枢电流之间的关系为Tem=CmIa;TL为负载转矩,它与负载电流之间的关系为TL=CmILa;Cm为电机转矩系数;J为负载的总转动惯量;n为转子转速。
将式(5)进行拉普拉斯变换可得:
Cm(Ia(s)-IaL(s))=Jsn(s)
(6)
由式(2)、(6)得出的电枢电压和电枢电流之间的关系为:
E(s)/(Ia(s)-IaL(s))=R/(Tms)
(7)
式中Tm——电机机械时间常数,Tm=JR/CmCe。
由式(4)、(7)得出的电机动态数学模型如图1所示[3]。
在图1中,如果要采用电流环控制,则M是
电流给定点、N为电流反馈点。电机的电气时间常数Ta要远远小于电机的机械时间常数,所以电枢电流的变化速度远远大于电枢反电动势的变化速度,在设计电流环时可忽略电枢反电动势的影响[4]。
忽略负载电流的作用,建立电流环速度环控制双闭环控制动态数学模型,如图2所示,其中Gv(s)是速度环控制器;Ga(s)是电流环控制器;G0(s)是机械谐振环节,用二阶振荡环节来模拟;Uv(s)是速度给定值;Ua(s)是电流给定值。

图2 直流电机速度环、电流环双闭环控制动态数学模型
图2中G0(s)为机械谐振环节,用二阶振荡环节来模拟,相应的表达式为:
G0(s)=[(1/ωn)2s2+2ζ(s/ωn)+1]-1
(8)
在图2中假设电流环控制器为纯比例控制,则有:
Ga(s)=k1
(9)
则电流闭环的控制传递函数为:
φa(s)=k1R-1(1+k1R-1)-1/[Ta(1+k1R-1)-1s+1]
=k1R-1(1+k1R-1)-1/(Ta′s+1)
(10)
其中,Ta′=Ta/(1+k1/R)为控制系统新的电气时间常数,是没有电流环控制时的电气时间常数的1/(1+k1/R)倍。此时速度环的控制对象传递函数为:
Gv0(s)=φa(s)RG0(s)/CeTms=G0(s)k1(1+k1R-1)-1/
[(CeTms)(Ta′s+1)]
(11)
设Ta′的倒数远远大于机械谐振频率ωn,即:
1/Ta′≫ωn
(12)
那么在控制对象机械谐振频率内,控制对象的一阶惯性环节可简化为纯积分环节[5],即:
Gv0(s)=φa(s)RG0(s)/CeTms
=G0(s)k1(1+k1R-1)-1/(CeTms)
(13)
在没有添加电流环控制的情况下,需要考虑电枢反电动势的影响,由图1中的电机数学模型
可以得到控制对象的传递函数Gv0′(s)=[Ce(TaTms2+Tms+1)]-1,一般有Tm>10Ta,则此式可简化为:
Gv0′(s)=[Ce(Tas+1)(Tms+1)]-1
(14)
由式(13)、(14)可知,在控制系统中加入电流环控制后,速度环的控制对象有较大改善,主要表现在:控制对象由0型系统变为Ⅰ型系统,控制对象由二阶惯性环节变为纯积分环节,提高了系统的型别,速度控制误差为零;增加了速度回路的相位裕度,由原来的-180°相位变为-90°相位,为增加速度环低频增益提供了条件,减小了回路的加速度误差[6]。
由上述分析可知,直流电机动态数学模型稍作变换即可得到另一种形式,如图3所示,N(s)为扰动力矩。
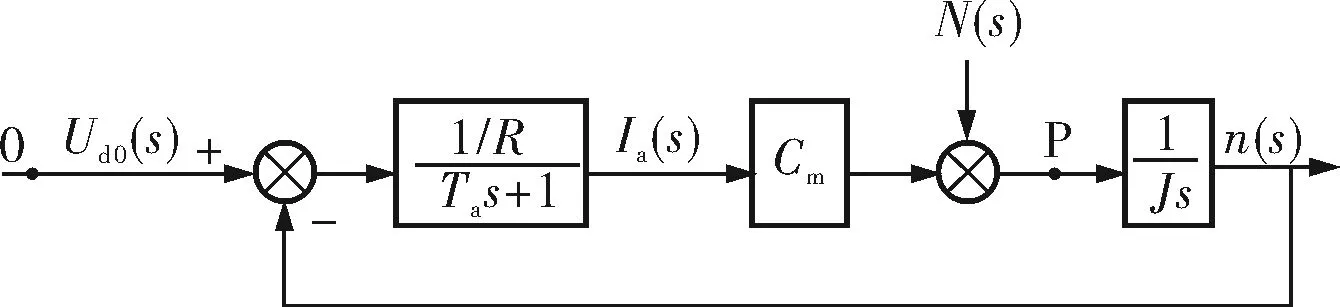
图3 带有扰动力矩的直流电机动态数学模型
无电流环时的速度控制数学模型如图4所示,其中速度环控制器Gv(s)=kv。

图4 无电流环的速度闭环动态数学模型
由图4可知,速度环闭环传递函数为:
φv(s)=ω(s)/Uω(s)=Cmkcv/[JLs2+
JRs+Cm(Cb+kcv)]
(15)
力矩扰动下的速度环闭环传递函数(即扰动力矩引起的速度扰动)为:
φvn(s)=ω(s)/N(s)=(Ls+R)/[JLs2+JRs+
Cm(Cb+kcv)]
(16)
在扰动力矩N(s)的作用下输出速度的稳态误差为:
Evn(s)=-φvn(s)gN(s)
(17)
在实际系统中,扰动力矩通常以阶跃形式出现,故假设N(s)=n0/s,那么根据拉普拉斯终值定理,可得扰动力矩作用下的速度误差稳态值:
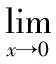
(18)
可以看出,为了抑制扰动力矩的影响,需要增加速度环放大倍数kcv。由于受到系统机械谐振频率的限制,速度控制器的放大倍数不能无限增加,速度误差也就不可能为零[7]。
带有电流环的速度回路数学模型如图5所示,其中Gv′(s)=kcv′,电流回路控制器Ga′(s)=kca′(1+1/Tis),N′(s)为力矩波动。

图5 带有扰动力矩的速度环、电流环动态数学模型
由图5可知,电流闭环传递函数为:
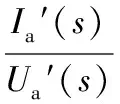
(19)
速度回路的闭环传递函数为:
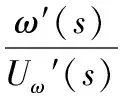
(20)
在扰动力矩作用下速度误差传递函数为:
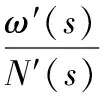
(21)
速度回路响应扰动力矩N′(s)输出端误差为:
Evn′(s)=-φvn′(s)gN′(s)
(22)
在实际系统中,扰动力矩通常以阶跃形式出现,故假设N(s)=n0/s,那么根据拉普拉斯终值定理,可得扰动力矩作用下的速度误差稳态值:
(23)
可见加入电流环后,速度回路响应扰动力矩N′(s)的稳态输出误差为零[8]。
2 速度环、电流环的实现
伺服控制器的工作原理如图6所示,主控制器采用具有浮点运算功能的F28335,信号采集与滤波采用FPGA(EP1C3),电流信号反馈采用LTSR15-NP,位置反馈元件采用圆光栅,电机驱动采用智能功率模块DRV8332[9]。控制回路内环为电流环,外环为速度环;电流控制器采用PID算法,闭环带宽保守可实现300Hz,远大于系统谐振频率,满足式(13)的假设条件;速度控制器采用超前滞后算法。
2.1信号采集与处理单元的硬件实现
FPGA具有的并行处理功能使其在信号采集与预处理和实现简单通信协议方面得到越来越广泛的应用。在此伺服控制器中,FPGA负责电流信号的采集与低通滤波处理,实现BISS和UART总线协议,作为协处理器。主处理器采用F28335,具有浮点运算功能,工作主频可达150MHz,主要实现复杂的控制算法[10]。控制板硬件结构与工作原理如图7所示。
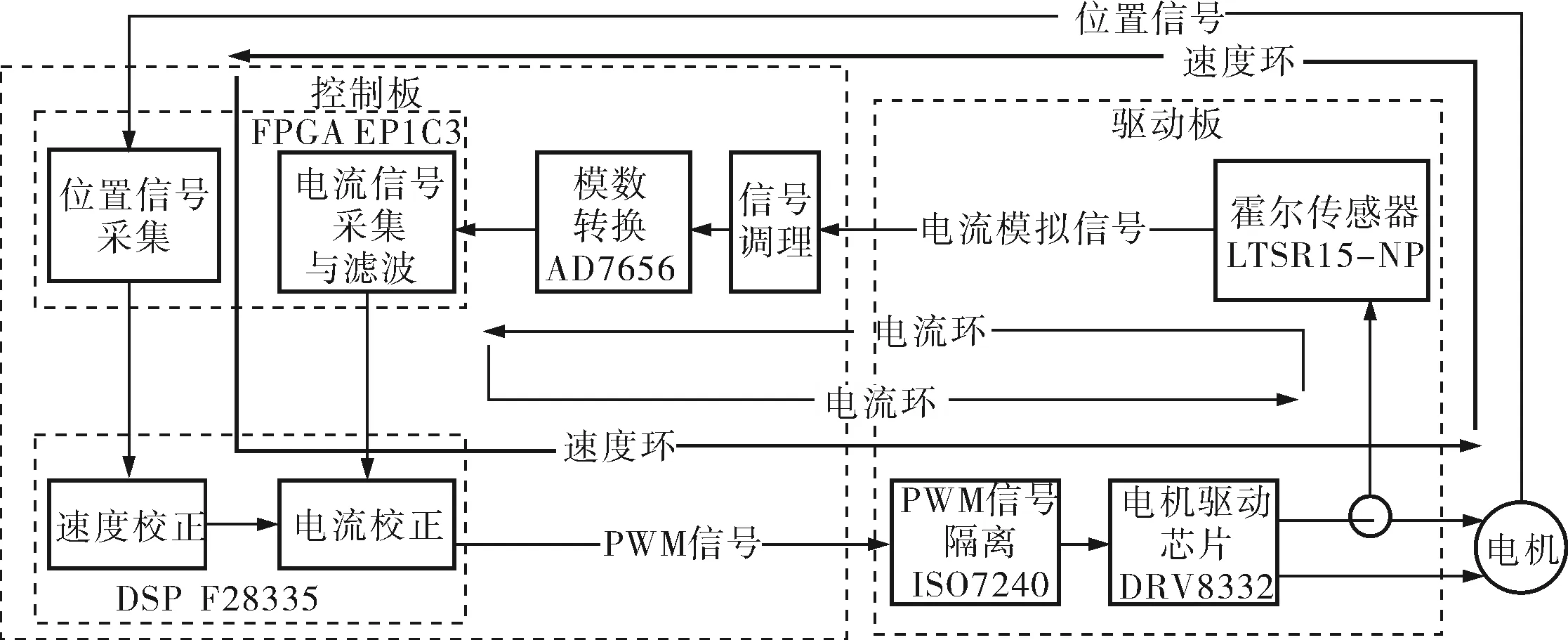
图6 伺服系统工作原理框图
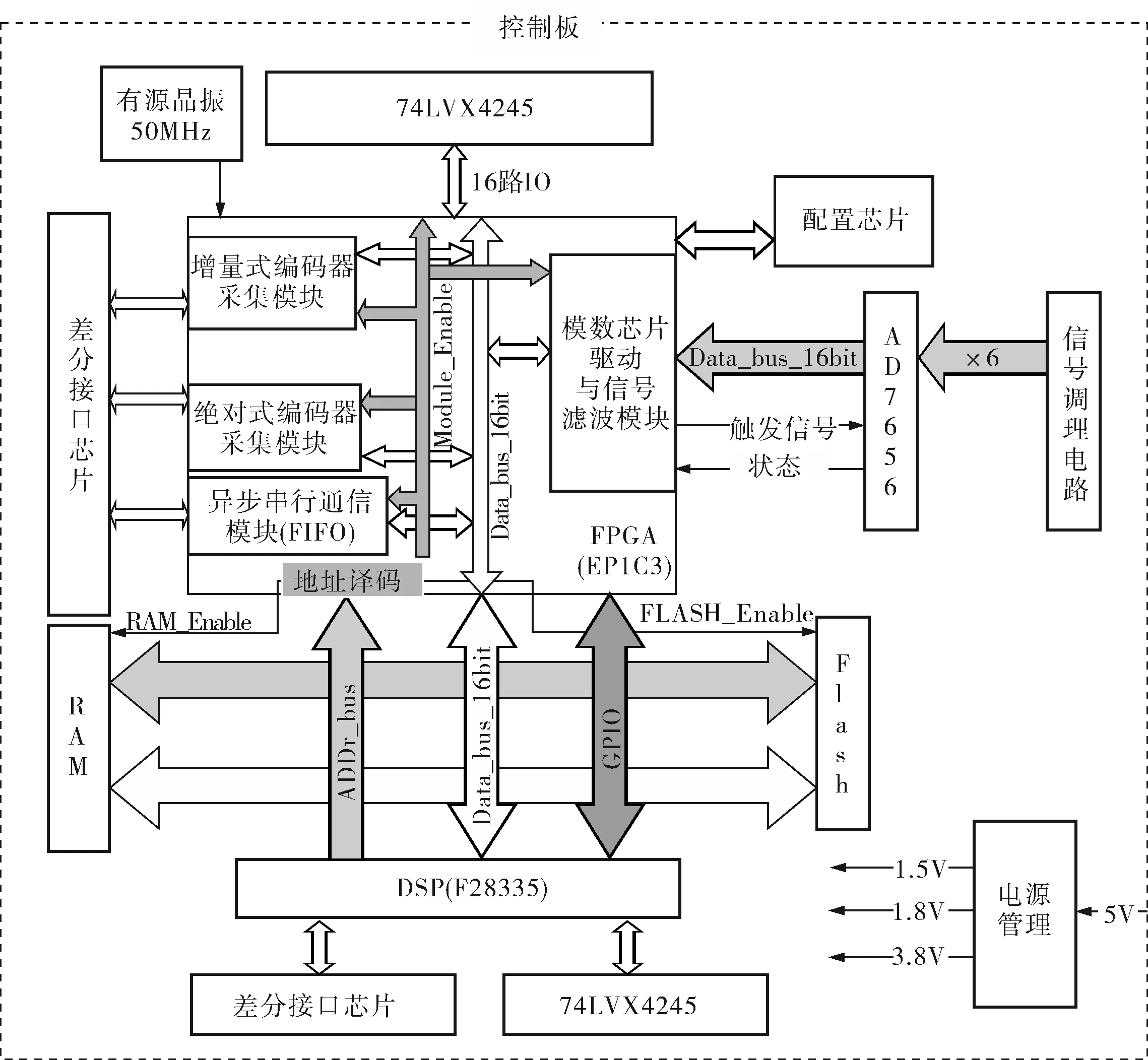
图7 控制板硬件结构与工作原理框图
FPGA以160kHz的频率触发模数转换芯片,接着采集转换结果,然后进行低通滤波处理(16次取平均),经过低通滤波后的实时数据输出速率为10kHz,与电流控制器的采样频率相匹配(10kHz)。FPGA将处理过的16位补码数据存放在16位的D触发器中,并将这16位D触发器作为一个寄存器映射到F28335的片外某一个地址总线上,使F28335可以直接读取电流反馈数据并进行电流校正[11]。
各种串行通信协议在嵌入式系统中应用十分广泛,通常采用专用通信芯片实现通信(如TL16C754),这样会增加系统的复杂程度和成本。本系统中涉及的串行通信包括BISS和UART,采用FPGA实现通信协议。BISS协议中可自由设定触发频率和通道数,UART协议中可自由设定波特率、FIFO深度和通道数,增加了系统的灵活性,使板级资源得到充分利用。将UART模块中的接收和发送FIFO分别映射到F28335地址总线中不同的地址上,F28335通过中断或查询方式获得UART模块的满或空信号后,可直接通过数据总线读取或写入通信数据。将BISS模块接收到的位置数据存放在3个16位寄存器中,并以1kHz的速度更新位置信息,满足速度环采样频率要求。分别将3个寄存器映射到F28335的地址总线上,F28335可以直接读取位置数据,进行速度校正[12]。
随着现代伺服控制中的伺服算法和控制逻辑日益复杂,对CPU的性能要求也逐渐增加。本系统选用F28335作为主控制器,具有浮点运算功能,工作主频150MHz,34KByte内部RAM、256KByte内部Flash,可以满足多轴三环控制系统的数据采集和控制算法实现。用F28335内部定时器设定10kHz电流环采样频率,在每个采样周期内读取FPGA中滤波后的电流反馈数据,与给定值做差,然后进行PID算法计算,将计算结果赋给比较寄存器以改变调宽波的占空比。将10kHz采样频率进行10分频得1kHz速度环采样频率,每个速度环采样频率读取FPGA中位置的反馈数据,差分后作为速度反馈值与速度给定值做差,然后进行双超前滞后算法计算,将计算结果作为电流环给定值,软件工作流程如图8所示。
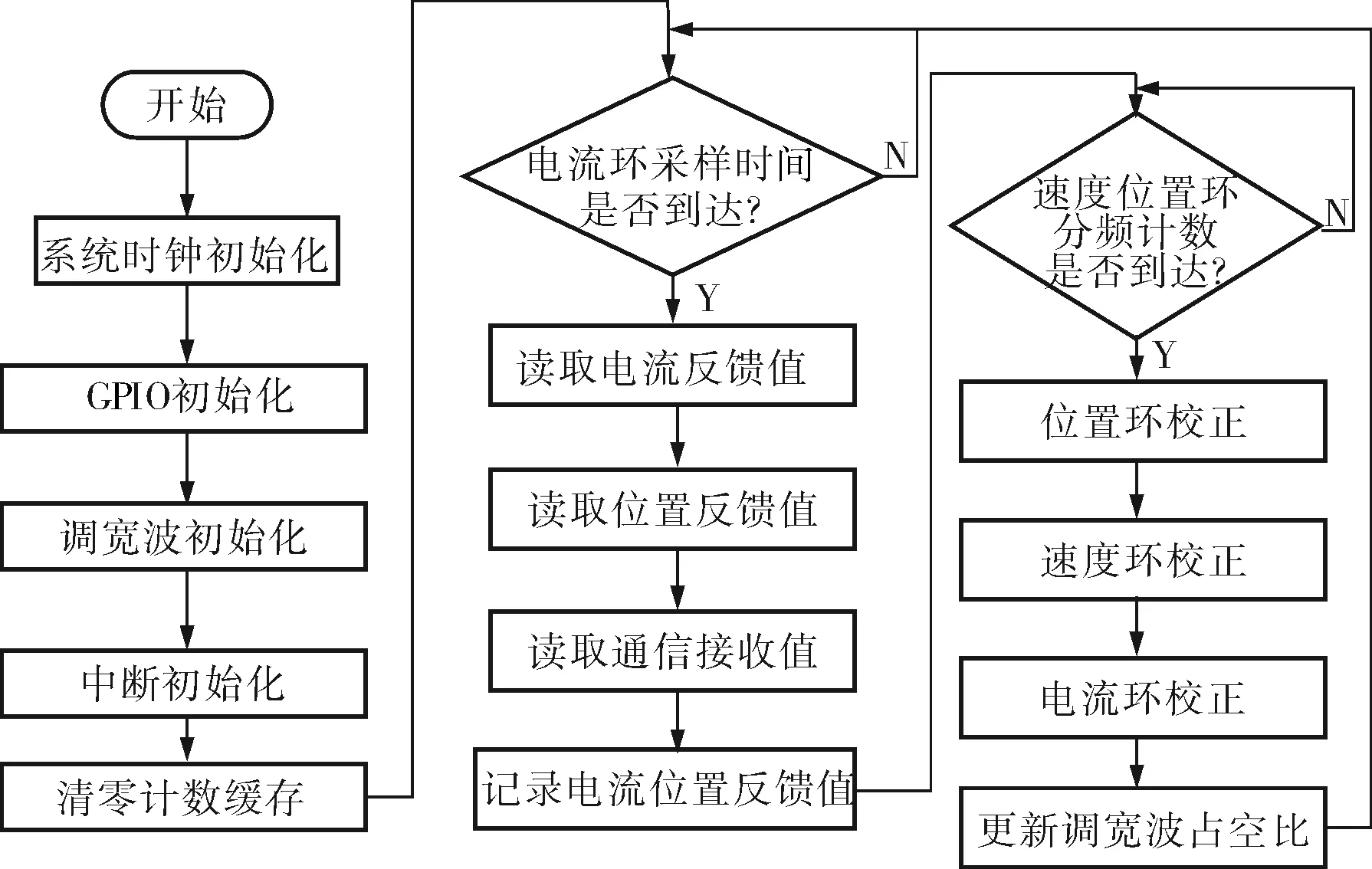
图8 软件流程
2.2功率驱动单元硬件实现
功率驱动核心部件采用IPM模块DRV8332,最高供电电压70V,最高运行频率500kHz,具有可编程的电流保护、过载、低压、短路和过热保护功能。强电与弱电间的隔离采用磁耦隔离ISO7240,具有更加简单的电路和可靠性,所占PCB板空间也更小。在功率模块输出级串接霍尔电流传感器LTSR15-NP,可测电流-15~15A,带宽(-0.5~0.0dB)100kHz。
3 实验结果
分别对控制系统的电流环和速度环进行测试,测试内容包括正弦跟踪和阶跃响应。
3.1电流环实验结果
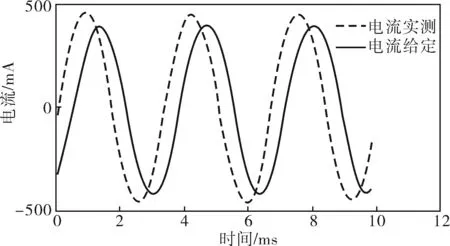
图9 电流闭环正弦跟踪曲线
进行输入为915mA的阶跃响应实验,电流实测值如图10所示。
3.2速度环实验结果
进行输入为5.5°/s的速度阶跃响应,速度实测值如图11所示,每个时间点为1ms。
给位置环输入一正弦信号:
P=θmaxsin(ωt)=20sin(0.5t)
(24)
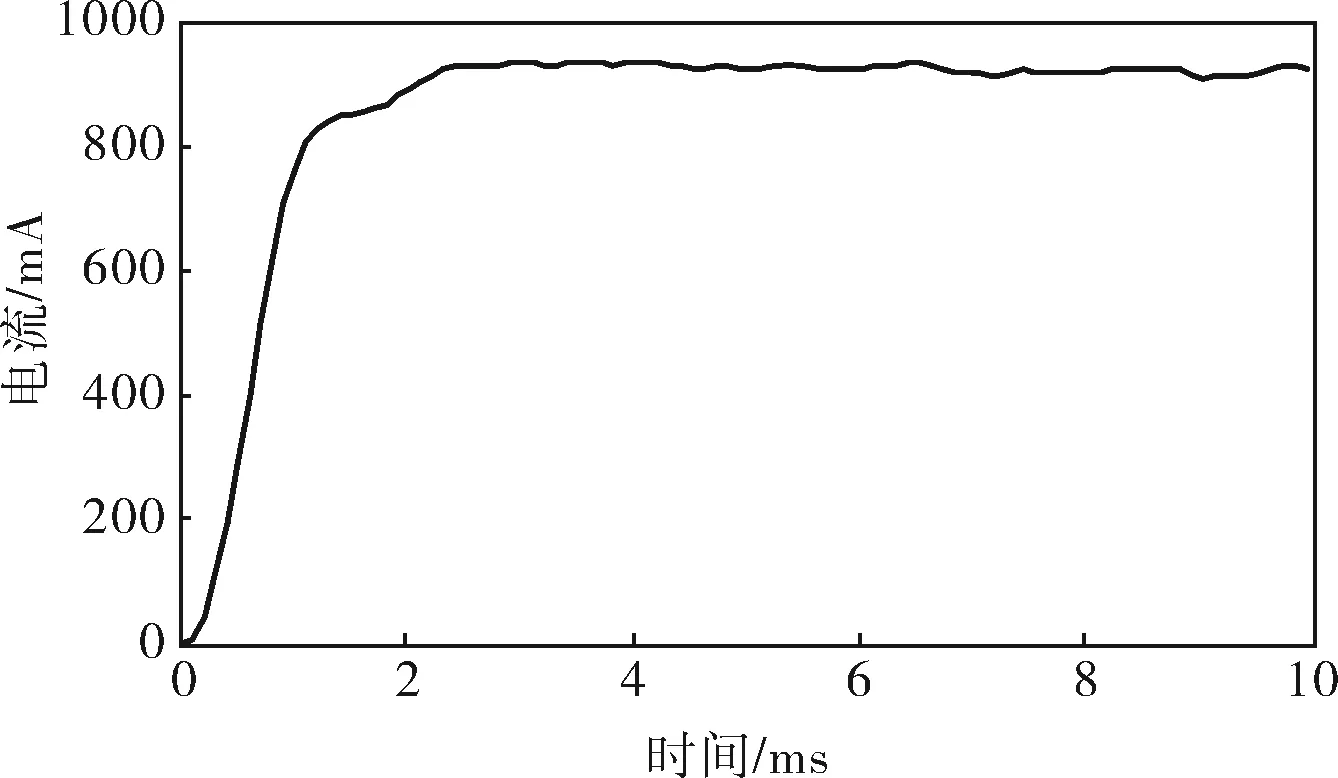
图10 电流闭环阶跃响应
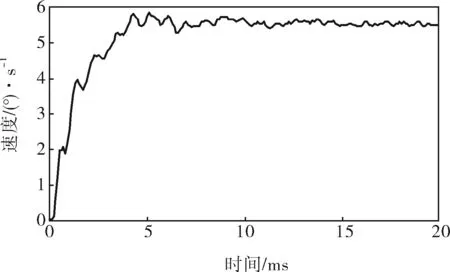
图11 速度闭环阶跃响应
图12为无电流环仅有速度环位置环时的跟踪误差,图13为既有电流环又有速度环和位置环时的跟踪误差。对比图12、13可以看出,电流环可以提高约五倍跟踪精度。
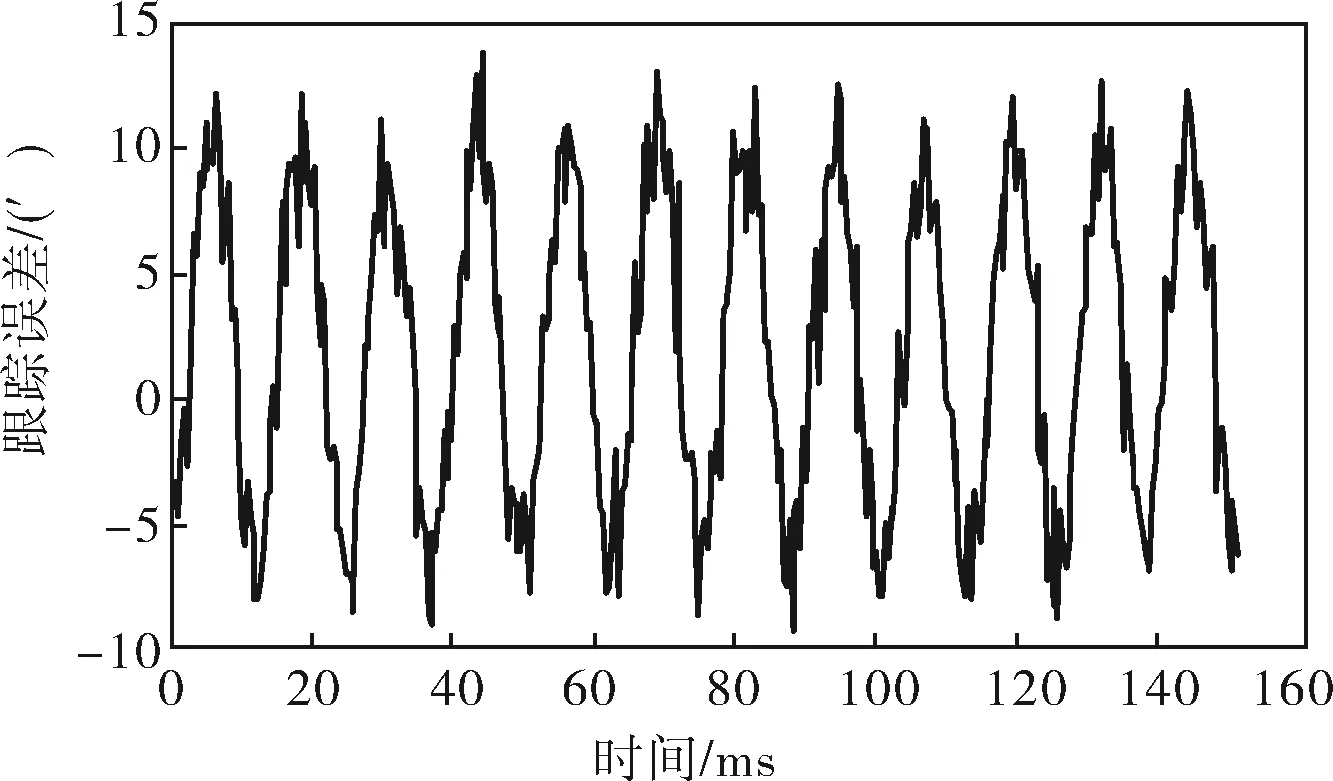
图12 无电流环时的位置跟踪精度
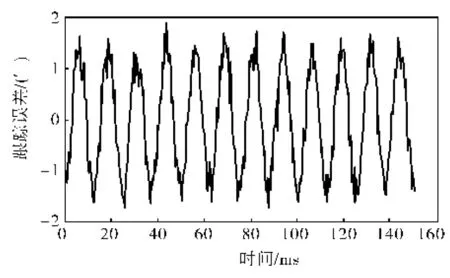
图13 添加电流环后的位置跟踪精度
4 结束语
首先从理论上证明电流环能够提高速度控制对象的型别,增加速度环相位裕度和低频增益;然后从硬件到软件算法实现方面详细地介绍了以DSP+FPGA为主控制核心的伺服控制器的设计。正弦跟踪和阶跃测试实验结果表明:电流环带宽和位置跟踪精度均与期望相符合,可进行下一步工程对比试验。
[1] 刘志明,陈黎,李清军,等.基于电机力矩波动抑制的电流反馈法[J].微计算机信息,2010,26(31):108~109.
[2] 熊皑,范永坤,吴钦章.光电跟踪系统力矩波动干扰抑制的研究[J].电光与控制,2009,16(4):72~74.
[3] 刘志明,陈黎,王德江,等.直流力矩电机力矩波动抑制方法比较[J].微型机与应用,2010,29(23):68~70.
[4] 庞新良,赵薇薇,范大鹏,等.直流力矩电机在机载光电伺服系统中的应用研究[J].红外技术,2007,29(10):573~578.
[5] 黄永梅,张桐,马佳光,等.高精度跟踪控制系统中电流环控制技术研究[J].光电工程,2005,32(1):16~19.
[6] 黄昌霞,李奇,姬伟,等.高精度稳定平台伺服控制系统设计与实现[J].航空兵器,2011,(1):23~27.
[7] Ellis G.Control System Design Guide[M].北京:电子工业出版社,2006.
[8] 王超,郝静如,李启光.一种基于DSP和多传感器稳定平台的设计[J].北京信息科技大学学报(自然科学版),2010,25(2):79~83.
[9] 李锦英,付承毓,于伟.直接驱动系统中力矩扰动的抑制[J].哈尔滨理工大学学报,2011,16(4):78~81.
[10] 毕永利,王连明,葛文奇.光电稳定平台控制系统中数字滤波技术的的研究[J].仪表技术与传感器,2005,(4):54~57.
[11] Ahmed S,Elhamid A.Cascade Control System of Direct Current Motor[J].World Applied Sciences Journal,2012,18(12):1680~1688.
[12] Ali Bekir Yildiz.Electrical Equivalent Circuit based Modeling and Analysis of Direct Current Motors[J].Electrical Power and Energy System,2012,43(4):1043~1047.
CurrentLoopforDCServoSystemBasedonDSP+FPGA
CHEN Jian, WANG Wei-guo, ZHANG Zhen-dong, JIANG Run-qiang
(CASChangchunInstituteofOpticsandFineMechanicsandPhysics,Changchun130033,China)
In the traditional servo control system composed of speed loop and position loop, the impact of torque fluctuations on the small inertia DC motor servo system can result in a slow moving accuracy. A way to reduce the impact of fluctuations in the moment by adding the current loop was proposed, including the corresponding way to realize the idea efficiently and economically, of which, a mathematical model of the DC motor was established and causes of the torque fluctuations were listed to analyze the effects of current loop in torque ripple suppression and the increase in the speed loop gain of the low-frequency theoretically. Regarding the high speed, real-time and large data of the current loop, the DSP+FPGA-based new servo controller and power module were designed, including the hardware and software. The experimental results show that a 300Hz-bandwidth current loop can effectively suppress torque ripple and the DC servo control system proposed can improve tracking accuracy while to be applied to the electro-optic theodolite.
current loop, moment disturbance, inner ring of current loop, mathematical model for DC motor, DSP+FPGA
TH862+.7
A
1000-3932(2016)02-0181-07
2015-11-23(修改稿)

