改进型Smith-专家PID算法在烘缸温度串级系统上的应用
张爱娟 胡慕伊 黄亚南
(南京林业大学 江苏省制浆造纸科学与技术重点实验室,南京 210037)
改进型Smith-专家PID算法在烘缸温度串级系统上的应用
张爱娟 胡慕伊 黄亚南
(南京林业大学 江苏省制浆造纸科学与技术重点实验室,南京 210037)
针对少烘缸或单烘缸纸机的干燥过程具有滞后大、惯性大且非线性的缺点,提出专家PID结合Smith预估器的算法,设计了少烘缸纸机或单烘缸纸机的烘缸温度和蒸汽流量串级控制系统。主控制器是改进的专家PID控制器,利用基于专家经验的知识库在线调整PID参数;对主回路采用改进型Smith预估器,以克服纯滞后对系统稳定性的影响,也解决了Smith预估器对数学模型精确要求的问题。利用MATLAB进行仿真,结果表明:改进型Smith-专家PID算法具有良好的控制品质,具有超调小及响应速度快等动态特性。
烘缸温度 专家PID 改进型Smith预估 串级控制
在造纸工业中,干燥部是消耗蒸汽相对较多的一个工段,目前来说使用最多的是烘缸干燥。烘缸温度是一个重要变量,对纸的平滑度、收缩性和物理强度都有影响,因此希望烘缸温度保持恒定,使纸张水分保持恒定,降低断纸率,提高生产率。同时它还影响所用的蒸汽量,与节能密切相关。合理、高效地对烘缸温度进行控制,可以改善纸张质量,降低能耗,因此设计一个高效的控制系统至关重要。
目前,国内多数造纸厂采用蒸汽压力控制烘缸温度,由于现实的客观原因,这种方法在多烘缸纸机上应用很多。相关研究者提出过烘缸温度的自适应模糊预估控制[1],纸机烘缸温度仿人智能控制[2]。对于烘缸温度等大时滞对象,最早是用单纯Smith预估器控制,后来发展到其与其他智能控制算法相结合[3],由于传统Smith预估器对模型要求高,提出改进型Smith预估器,并引入专家控制来进行温度调节[4],设计了一种适用于少烘缸纸机的改进型Smith预估器的专家PID的烘缸温度的串级控制系统。在此之前,有利用遗传算法对控制系统中的专家PID调节器参数进行优化的方案[5],有基于模糊PID和Smith预估器的串级温度控制方案[6]。笔者把改进型Smith预估器和专家PID控制结合起来,MATLAB仿真结果证明,该改进型方案使系统具有良好的动态性能和静态性能,对被控对象的适应能力强,鲁棒性和稳定性都较好。
在造纸厂中,由于烘缸温度控制回路的滞后时间大及烘缸表面温度不易测量等原因,因而常使用蒸汽压力的单回路来控制烘缸温度,如图1中虚线所画的单回路1所示。这种控制方法在多烘缸纸机上应用较多,利用饱和蒸汽压力和蒸汽温度的对应关系来控制温度。
针对少烘缸纸机或单烘缸纸机,在常规单回路的基础上对控制系统进行改进,设计了烘缸温度串级控制系统,烘缸温度作为主控对象,蒸汽流量作为副回路,如图1中的串级回路2所示。其中,主控制器为改进的专家PID控制器,来控制大滞后环节对系统稳定性的影响。副控制器为单纯的比例控制器,提高整个系统的响应速度,当蒸汽流量变化时就提前开始对烘缸温度进行调节。由于主回路的滞后大,副回路滞后较小,综合考虑系统的响应速度,在主回路上加入改进的Smith预估器来克服滞后的干扰。
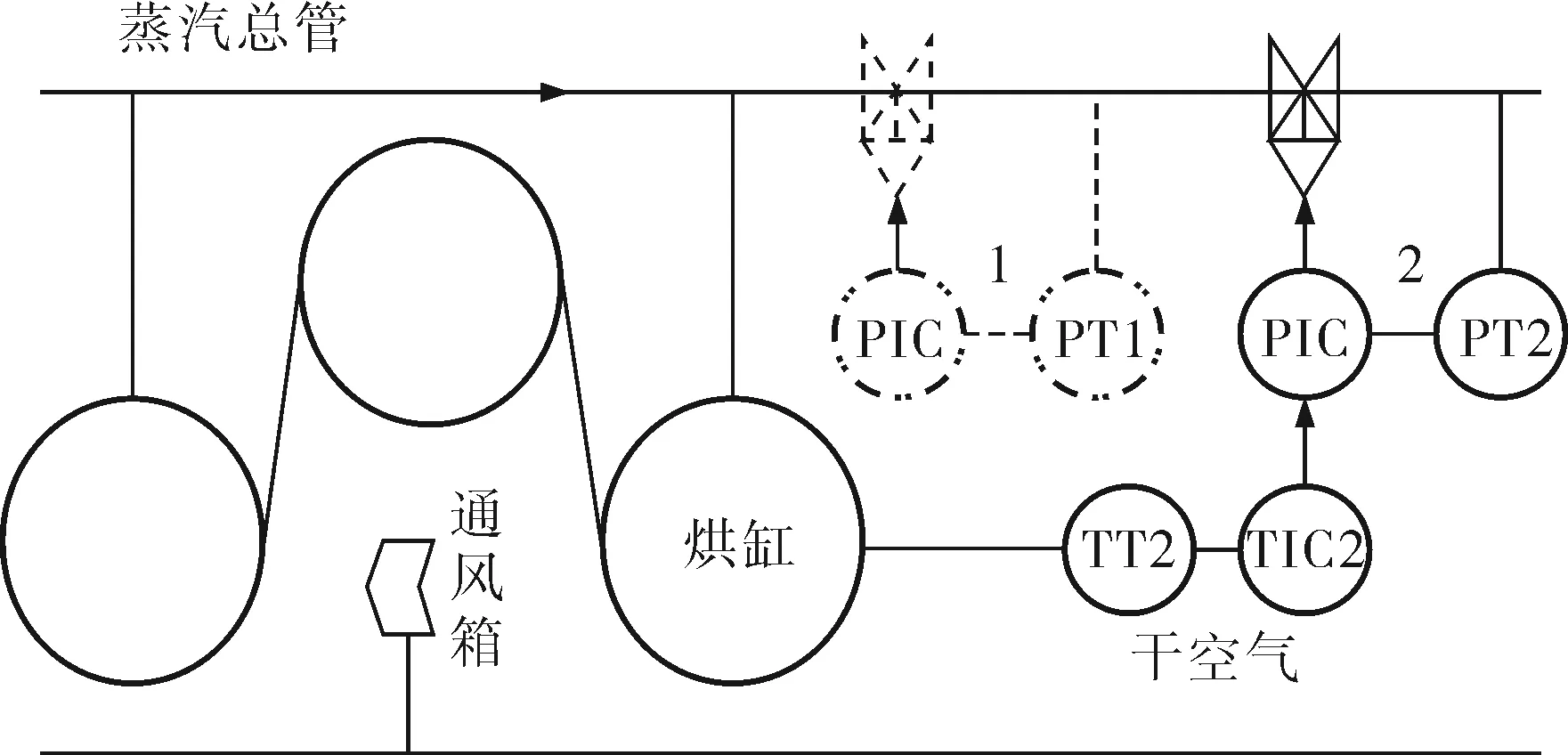
图1 改进后单烘缸温度控制系统
在干燥初期,纸张含水量高,干燥率大,所需热量少;后期干燥率下降,需要的热量增大,要求烘缸表面温度有一个正确分布,即烘缸温度曲线[7]。因此,烘缸干燥曲线就直接影响了干燥能力和蒸汽用量。文献[8]对干燥曲线的参数进行优化,得到的优化曲线应用后控制效果良好。笔者根据优化的温度曲线,设定单烘缸的温度并控制。单个烘缸按照优化后的温度曲线来设定一个温度值。高温部分的蒸汽处理后可循环到低温部分对烘缸进行供热,节约蒸汽用量。
2 改进型Smith预估的专家PID控制系统
2.1烘缸温度控制系统的总体结构
干燥部的烘缸温度环节惯性大、滞后大,因此,设计串级控制系统对温度进行控制。在烘缸温度控制系统中,蒸汽流量的波动是最主要的干扰,需选取蒸汽流量作为副回路控制对象,烘缸温度为主回路控制对象,构成一个串级控制系统。
在烘缸温度与蒸汽流量的串级控制系统中,主控制器为改进的专家PID控制器,副回路为提高响应速度,选用常规的比例控制器。另外,为补偿主回路温度环节的大滞后特性对整体系统稳定性的影响,在主回路加入了Smith预估控制器。传统的Smith预估器对被控对象的模型要求高,此处引入改进型Smith预估控制器,来克服被控模型变化时,控制效果变差的问题。控制系统结构如图2所示。
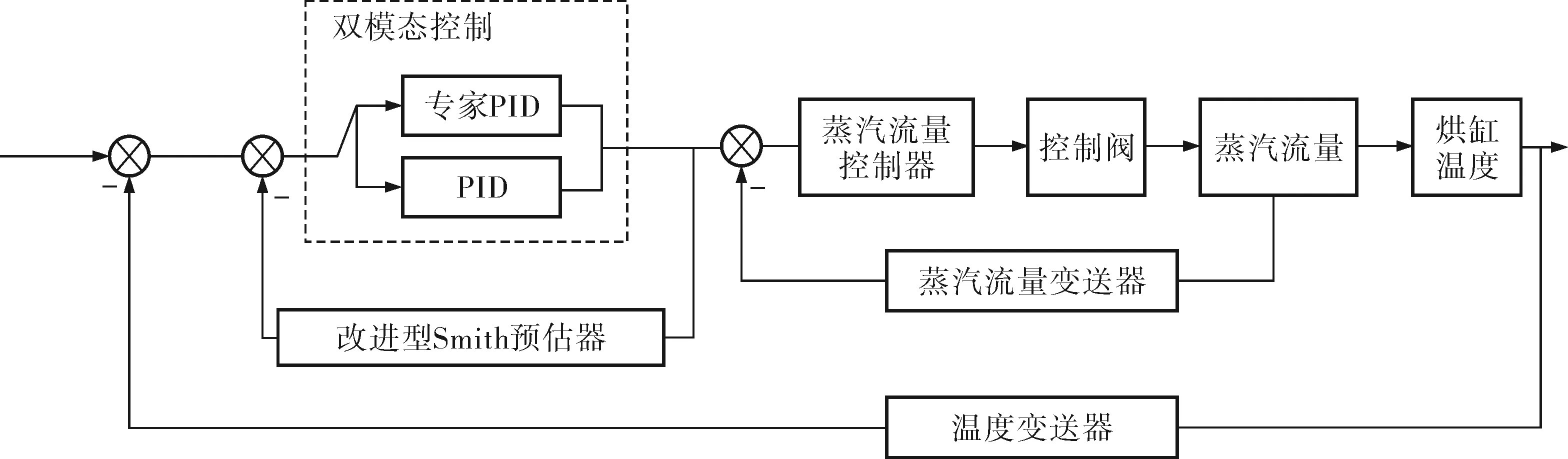
图2 控制系统结构
2.2专家PID控制器设计
专家PID控制就是在PID的基础上利用专家系统知识库中的规则推理得到的输出来调整PID的参数。在大滞后温度系统中,用基本的PID控制会有超调量或者调节时间过长的问题,所以引入专家控制。专家系统在化工中主要用来进行过程设计与综合,模拟与仿真和故障诊断,把专家控制应用到过程控制中不是要取代PID或其他算法,而是与它们结合[9]。所设计的专家PID控制器是间接专家控制,即利用专家系统中的知识库里的规则表来决定输出的PID参数。
另外,对专家控制器的算法进行改进,在烘缸温度偏差e<0.1时,采用常规的PID控制,获得较高的控制精度和较快的响应速度。在温度偏差较小时,只用 PID控制即可,可以减少控制规则的运算,提高速度。
2.2.1专家PID控制器结构
结合控制对象,专家PID控制器的结构如图3所示。
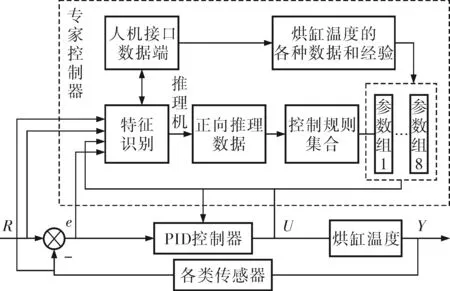
图3 专家PID控制器结构
由图3可以看出专家PID控制器[10]主要包括:
a. 知识库和推理机。这两者是专家控制器必不可少的组成。知识库里面存放和烘缸温度有关的各种数据和经验,它广义上包括数据库和规则库。规则库是核心内容。根据专家经验,建立一个输入为烘缸温度偏差和烘缸温度偏差变化,输出为PID参数的知识库。推理机主要是根据现场实时的运行状况和规则库来推出实际输出,采用数据驱动的正向推理。
b. 参数组。参数组是在不同情况下的控制参数,参数组与规则库相对应。参数组分别对应温度偏差变化时PID参数的大小。参数组与控制规则相互对应。
c. PID控制器。专家PID实际上就是间接利用专家经验来达到调整PID参数的作用,因此,专家PID的基础组成是常规PID控制器。最终的控制作用还是由PID的3个参数来实现;另外,当误差较小时,采用常规PID来单独控制以提高响应速度。
2.2.2专家PID控制规则集
专家控制规则集是专家PID控制器的核心部分,是关于烘缸温度控制系统的各种经验规则。主要包括:根据烘缸温度的偏差和偏差变化乘积PID参数的规则;控制过程异常或紧急状况的规则。
根据现场实际控制烘缸温度的经验,对烘缸温度的控制规则进行总结,得到最的专家控制规则如下:
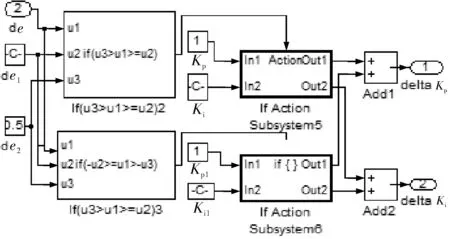
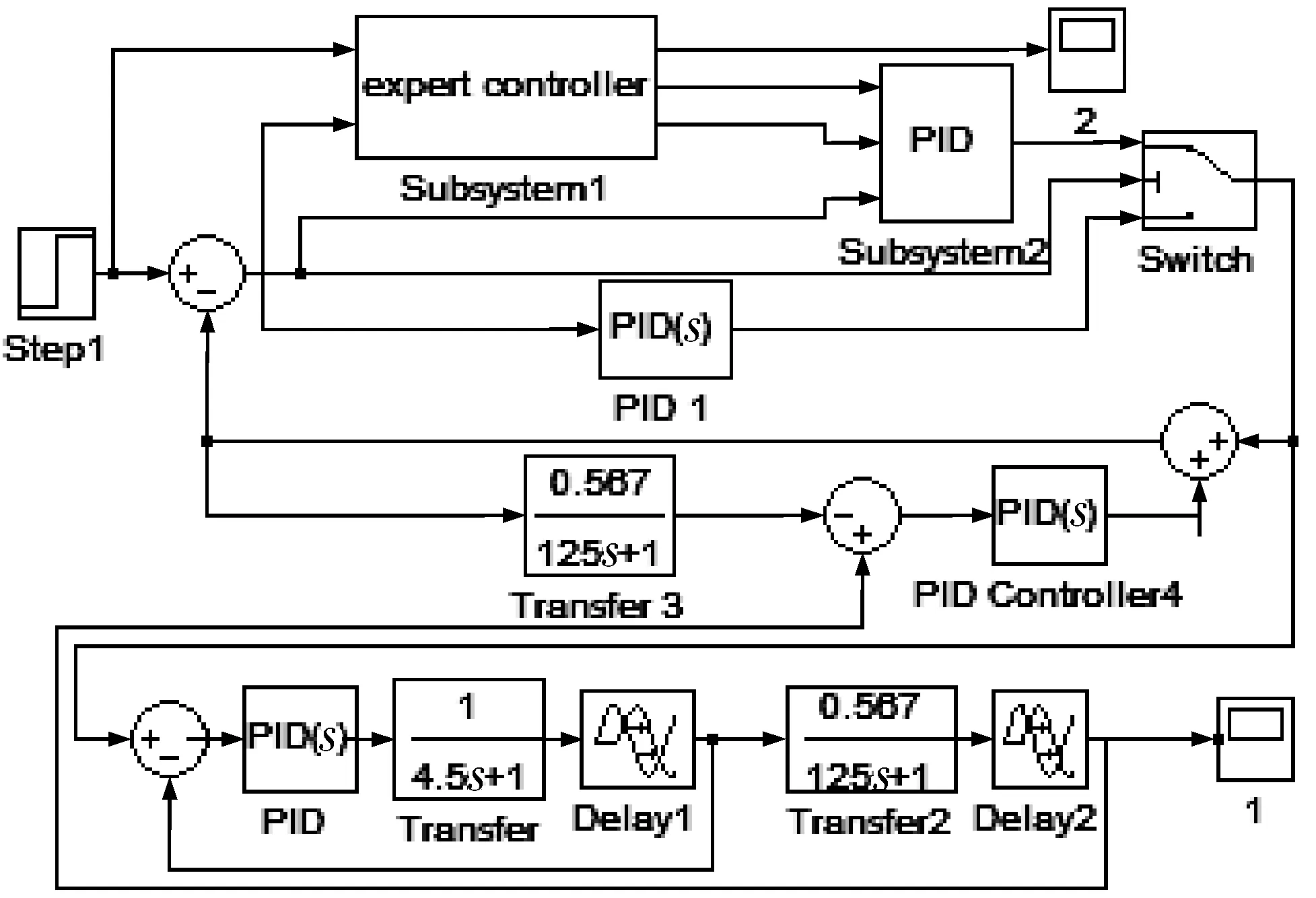
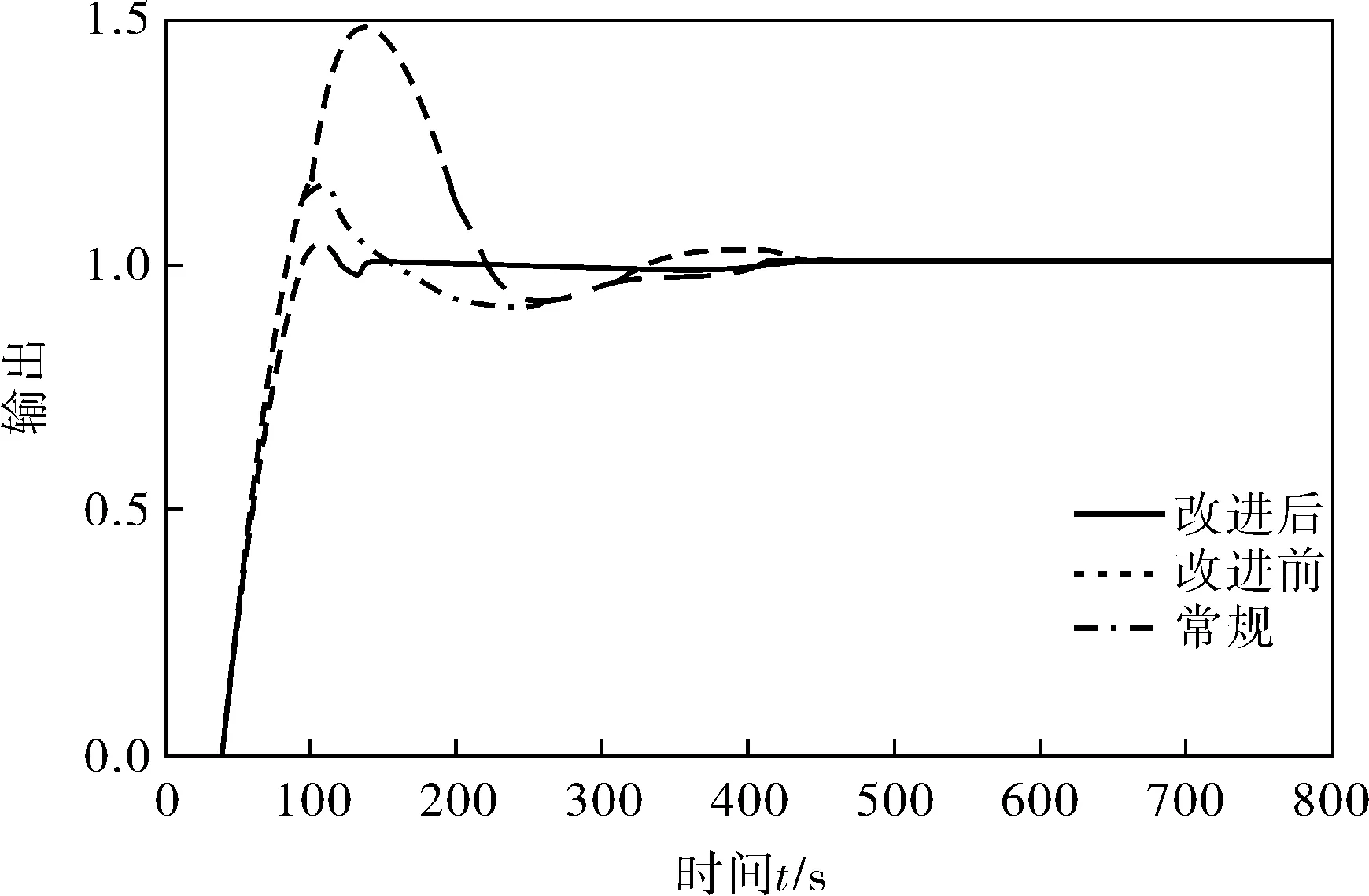
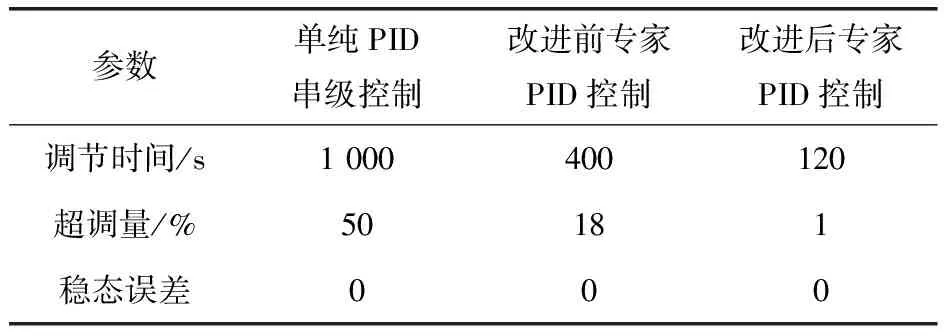
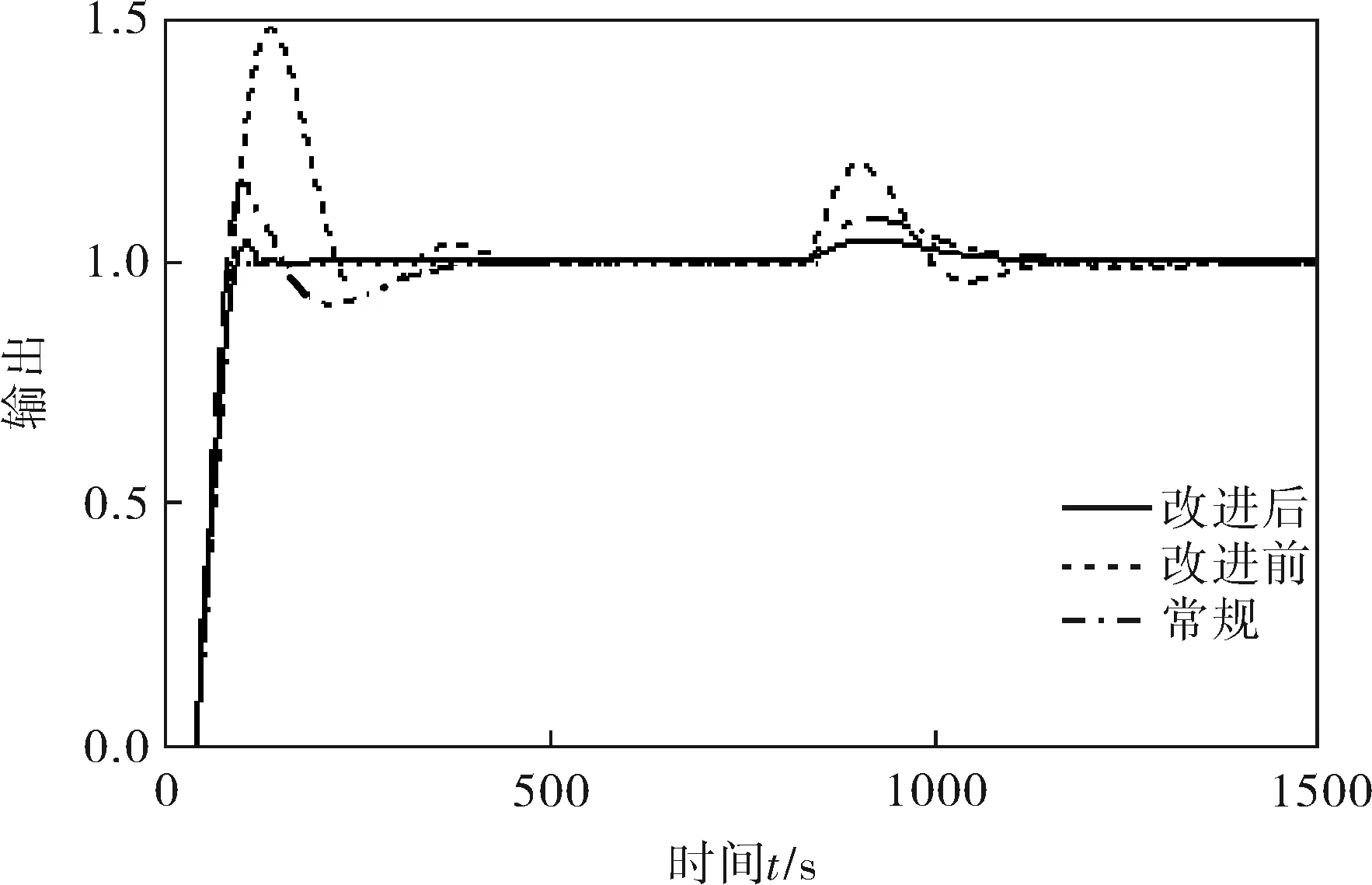
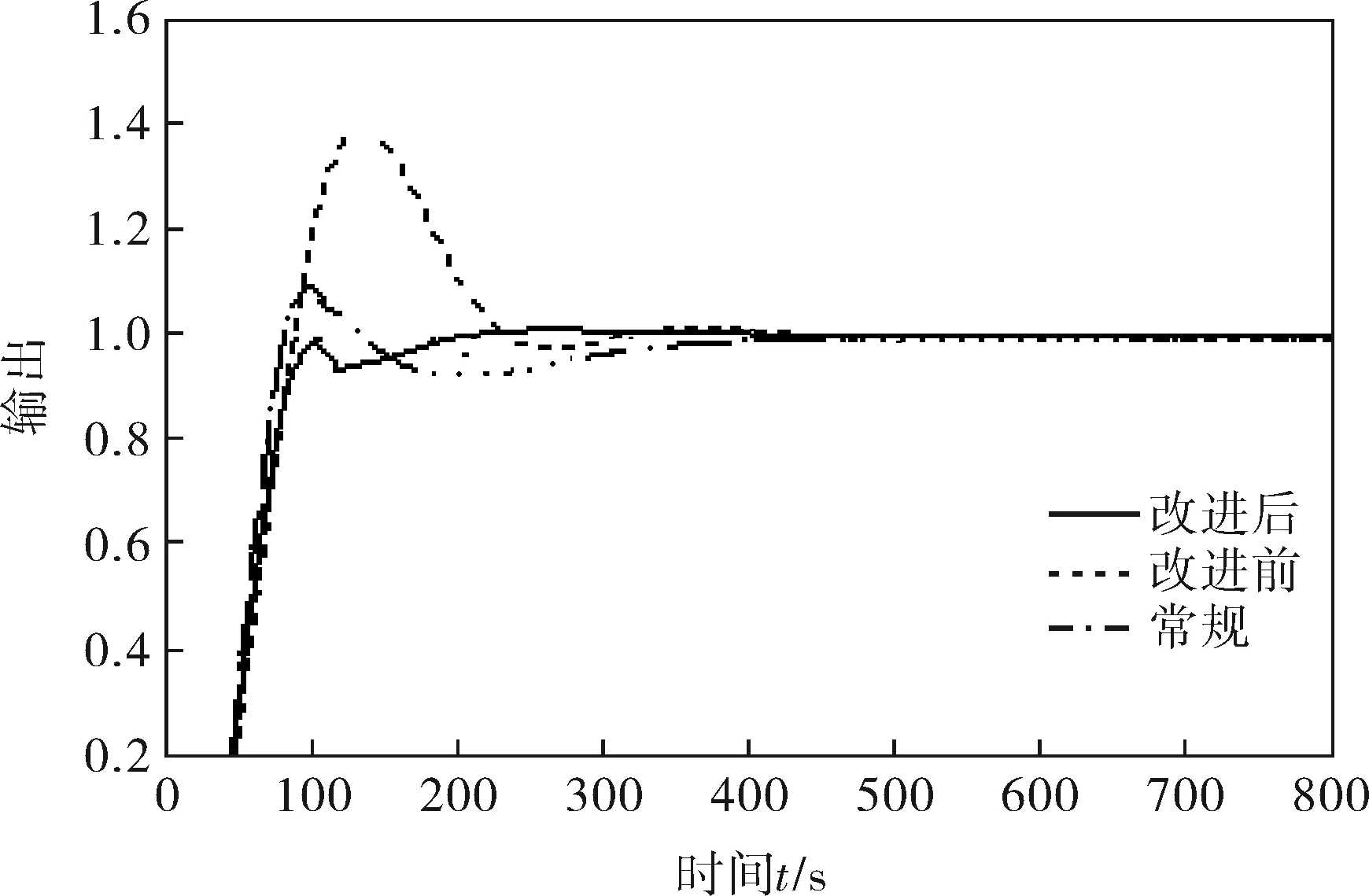
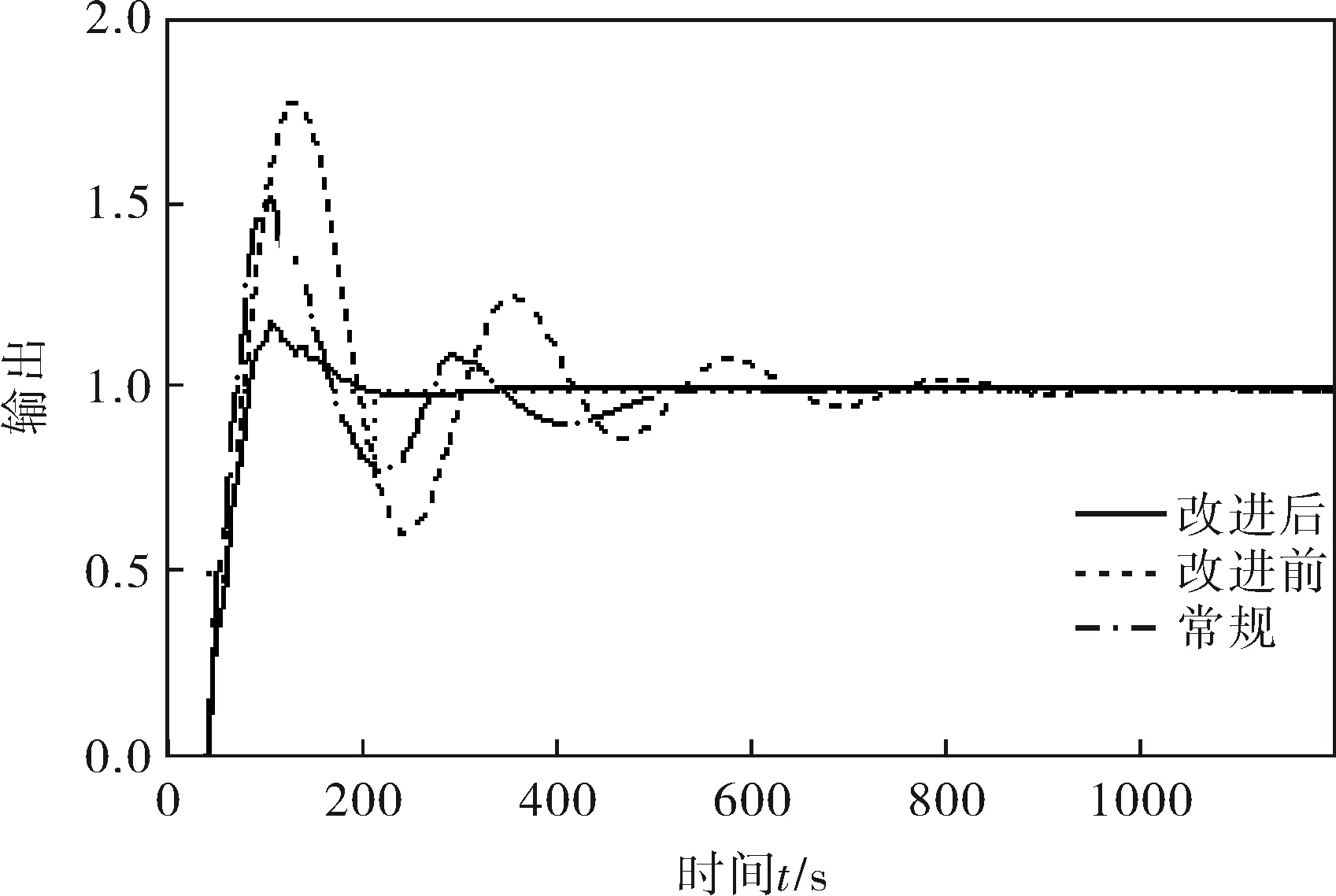
a. 如果烘缸温度偏差在a1、a2间,则比例参数设为c1,即IFa1≤e(k) b. 如果烘缸温度偏差在-a1、-a2间,则比例参数设为c1,即IF -a2≤e(k)<-a1,THEN ΔKp=c1; c. 如果烘缸温度偏差大于a2,则比例参数设为c2,即IFe(k)≥a2,THEN ΔKp=c2; d. 如果烘缸温度偏差小于-a2,则比例参数设为c2,即IFe(k)≤-a2,THEN ΔKp=c2; e. 若温度设定值改变,且使温度偏差变化在b1、b2间,则提高比例参数和积分参数,即IFb1≤e(k) f. 若温度设定值改变,且使温度偏差变化在-b1、-b2间,则提高比例参数和积分,也即IF-b2≤e(k)<-b1,THEN ΔKp=c1、ΔKi=d1; g. 若温度设定值改变过大,温度偏差变化大于b2,提高比例参数,降低积分参数,即IFe(k)>b2,THEN ΔKp=c2、ΔKi=d1; h. 若温度设定值改变过大,温度偏差变化小于-b2,提高比例,降低积分参数,即IFe(k)<-b2,THEN ΔKp=c2、ΔKi=-d1。 已知输入为温度偏差和温度偏差变化,输出为PID参数。为了实现专家规则,首先要把输入量温度偏差、温度偏差变化和输出量PID参数模糊化: e(k)={-a2,-a1,0,a1,a2} Δe(k)={-b2,-b1,0,b1,b2} ΔKp(k)={-c2,-c1,0,c1,c2} ΔKi(k)={-d2,-d1,0,d1,d2} 其中,e(k)为k时刻烘缸温度偏差;Δe(k)为k时刻温度偏差变化;ΔKp(k)为k时刻比例参数变化量;ΔKi(k)为k时刻积分参数变化量。 2.2.3专家自学习算法 专家控制对被控对象模型要求不高,所以建立的控制规则可能随着现场工况改变就不适用。因此专家控制必须具备自学习能力,根据控制现场的实际情况来修改控制规则中的参数。以第h条规则来说明专家控制器修改参数m2的过程为例。修正过程是确定一个阀门开度变化ΔV(k)最小值mmin,当实际测量值小于设定值,则m2减去mmin;若大于设定值,则m2加上mmin。修正算法可描述为: IFe(k)Δe(k)<-b2THEN ΔV(k)=m2 (IFe(k+1)≤-b2ANDe(k)Δe(k+1)=0 THENm2=m2+mmin IFe(k+1)≥b2ANDe(k)Δe(k+1)=0 THENm2=m2-mmin) 规则中的其他参数的修正也利用这种自学习算法。它可以保证规则集里的参数实现更新,适应现场模型参数的变化,使控制效果变好。 2.3改进型Smith预估器设计 对于像烘缸温度这样的大滞后系统,加入的Smith预估控制器可以控制时滞环节对整个系统稳定性的影响。但Smith预估的前提是要求有精确的数学模型[11],实际中如果被控对象的数学模型变化,控制的效果就会大为减弱,而实际上被控对象的模型一般都会发生变化,因此,要对原有的Smith预估器进行改进。 改进型Smith预估器的思想是当被控对象模型发生变化时,把变化后的模型与之前的模型的差值作为补偿器的输入,这样作为系统的反馈回路,如图4所示。 图4 改进型Smith控制器结构 其中,输出与给定间的传递函数为: (1) 因此,系统的特征方程为: (2) 若补偿器Gc2(s)的模很小,则: 1+Gc2(s)G0(s)e-τs≈1 (3) (4) 此时,特征方程近似为: (5) 因此,从式(5)可以得出系统的稳定性与被控对象模型中的时滞和所选取的补偿器都无关。 3.1仿真控制模型 在MATLAB中利用改进的专家PID算法对烘缸温度控制系统进行仿真[12],要实现仿真最主要的是专家PID控制器的建立,即专家规则的表述,以第e、f条规则为例,在Simulink中建立如图5所示的仿真模型。同理,在专家控制器的子系统下面依次建立专家控制规则表中的每一条规则,就能完整地把专家规则用Simulink模块建立表达。 最后,按照上面所建专家控制器和前述烘缸温度-蒸汽流量串级控制系统构建完整的仿真模型图(图6)。然后开始调试仿真,根据实际的经验值和试凑法,把专家控制规则表中的参数一一具体化,就可以调试出基于Smith预估的专家PID算法的实际仿真效果图。 图5 专家控制规则的仿真模型 图6 烘缸温度控制系统仿真模型 3.2正常情况下的仿真结果 根据上面建立好的仿真模型,利用辨识出的传递函数作为仿真对象,其中烘缸温度和蒸汽压力的传递函数模型分别为: (6) (7) 当参数模型匹配时,在t=0时刻对烘缸温度系统加入阶跃干扰,最后常规串级PID、改进前无Smith预估的专家控制器、改进后的专家PID控制,这3种不同的控制方案的响应曲线如图7所示。可以看出:改进前的专家控制系统(即没有加入Smith预估控制器的系统),控制效果比常规PID算法好,但是效果劣于改进后的专家控制系统。改进后的专家控制系统的响应速度最快,超调量最小,稳定性也较好。由图7和表1可看出,改进后的专家PID控制器很好地改善了大滞后环节对系统稳定性的影响,使系统阶跃响应曲线的超调量和响应时间都明显减小,稳定性变好。 图7 基于正常情况时3种控制方案的阶跃响应 参数单纯PID串级控制改进前专家PID控制改进后专家PID控制调节时间/s1000400120超调量/%50181稳态误差000 3.3加干扰时的仿真结果 当被控对象的模型参数不变化时,在仿真的800s时刻在副环加入一个向上的阶跃干扰,对比不同方法抗干扰的能力和稳定性。3种控制方案对应的响应曲线分别如图8所示。 图8 加入干扰后3种控制方案的阶跃响应 从仿真图看出,当在副环加入干扰后,改进后的Smith专家PID控制方案抑制干扰的能力最好,由干扰引起的超调和过渡时间都最小,系统稳定性好。 3.4模型参数变化时的仿真结果 图9 模型变化情况一下的阶跃响应 图10 模型变化情况二下的阶跃响应 从图9、10可知,当模型参数变化时,改进型Smith预估的专家PID控制可以较好地适应对象,无论是模型的增益和滞后变大还是变小,改进后的控制方案都优于常规方法和改进前的方案。可见改进型的Smith预估器克服了对精确被控模型的要求,与专家控制结合起来对控制对象具有适应性,提高了实际应用性。 针对单烘缸温度控制系统的大滞后、大惯性等特性会对系统的稳定性造成大影响的问题,引入基于专家规则库的专家PID控制算法。并结合改进型Smith预估控制器,构建了烘缸温度与蒸汽流量的串级控制系统,利用蒸汽流量来超前控制单烘缸温度。通过MATLAB仿真实验,可得出改进后即加入Smith预估器的专家PID算法对大时滞系统控制效果良好,响应速度快且超调小,受干扰后的鲁棒性好,而且当被控模型参数在一定范围变化时,该方案具有很好的适应性,仍有较好的控制效果。 [1] 任德均,姚进,王庸贵.抄纸过程中烘缸温度的自适应模糊预估控制[J].中国造纸,2003,22(6):23~26. [2] 张开生,李强华,张攀峰.纸机烘缸温度的仿人智能控制方法研究[J].中国造纸,2007,26(3):36~38. [3] 宋云霞,朱学峰.大时滞过程控制方法及应用[J].化工自动化及仪表,2001,28(4):9~15. [4] 谢志强,谢志刚,谢卿贤.基于专家经验的温度串级多路自动调节系统[J].化工自动化及仪表,1999,26(4):16~19. [5] 王学武,谭得健,郭一楠,等.基于GA的专家PID控制[J].化工自动化及仪表,2002,29(4):35~37. [6] 张燕红.模糊PID-Smith串级控制在加热炉温度控制系统中的应用[J].化工自动化及仪表,2012,39(8):979~981. [7] 吴一帆,罗可.纸机烘干部的计算机集散控制[J].长沙电力学院学报(自然科学版),1999,14(1):34. [8] 卢涛,沈胜强,李素芬.纸页干燥过程的数值模拟与参数分析[J].中国造纸学报,2003,18(1):119~123. [9] 张杰,张素贞.专家系统的发展及其在化工生产中的应用[J].化工自动化及仪表,1996,23(3):3~11. [10] 尹朝庆,尹皓.人工智能与专家系统[M].北京:中国水利水电出版社,2001:137~150. [11] 陈显枝,陈冲.基于专家系统的Smith预估器[J].工业控制计算机,2005,18(6):27,79. [12] 刘金琨.先进PID控制MATLAB仿真[M].北京:电子工业出版社,2011:296~300. ApplicationofImprovedSmith-ExpertPIDAlgorithminDryerTemperatureCascadeControlSystem ZHANG Ai-juan, HU Mu-yi, HUANG Ya-nan (JiangsuProvincialKeyLaboratoryofPulpandPaperScienceandTechnology,NanjingForestryUniversity,Nanjing210037,China) Considering large delay and inertia and nonlinearity of drying process which has less or single dryers in papermaking industry, the Smith-expert PID algorithm was proposed and the cascade control system for both dryer temperature and steam pressure was designed. The main controller is an expert PID controller which adopts expert advice-based knowledge base to adjust PID parameters; and the main loop employs an improved Smith predictor which can remove dead time influence from the system stability and satisfy Smith predictor for an accurate mathematical model. Simulation result shows that the improved Smith-expert PID control has good quality like small overshoot and fast response. dryer temperature, expert PID, improved Smith predictor, cascade control TH165+.2 A 1000-3932(2016)02-0128-06 2015-12-23(修改稿)基金项目:江苏省制浆造纸科学与技术重点实验室开放基金资助项目(201010)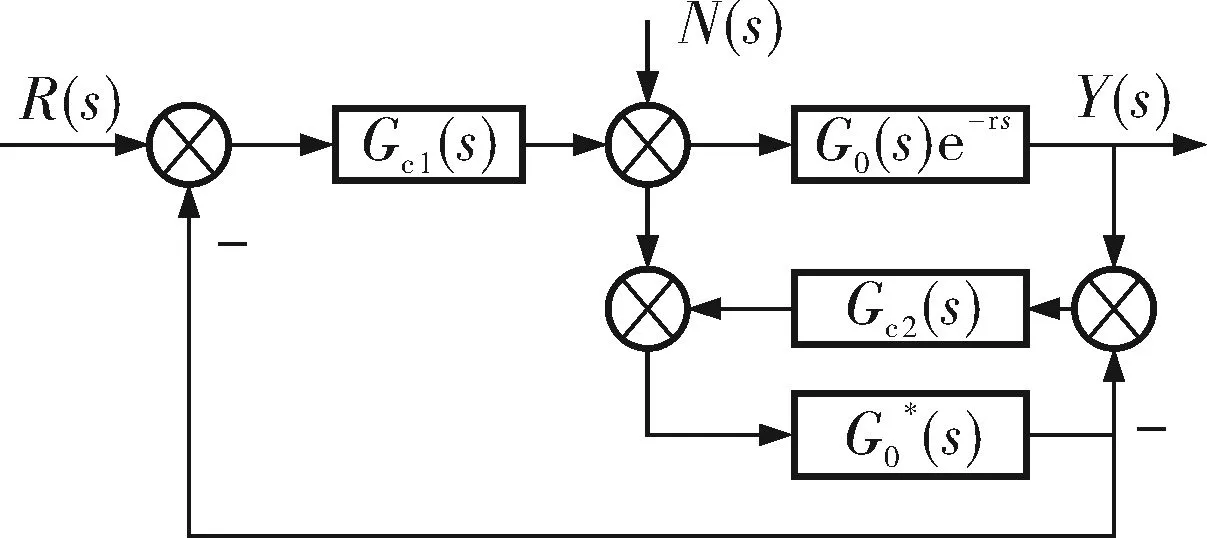
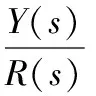
3 MATLAB仿真分析
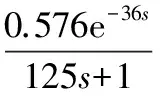
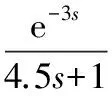
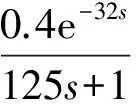
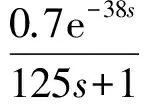
4 结束语

