提炼本质注重模式辨别——一道高考题的解法赏析

☉江苏省梅村高级中学　范永明

提炼本质注重模式辨别——一道高考题的解法赏析

☉江苏省梅村高级中学范永明

2016年高考已落下帷幕，全国1卷理科试题21题设计立意鲜明，角度宽，视点多，深入考查了数学理性思维.深化能力立意是数学命题一直以来的追寻目标，本试题真正地体现了“以能力立意为指导，以考查能力和素质”的命题原则.

一、题目呈现

（2016年全国1卷理科第21题）已知函数f（x）=（x-2）· ex+a（x-1）2有两个零点.

（1）求a的取值范围；

（2）设x1，x2是f（x）的两个零点，证明：x1+x2＜2.

二、试题简评

本题题面短小精悍，立意清晰，解法灵活，显现能力.作为一道压轴题，以函数零点为载体，主要考查导数在研究函数性质与证明不等式中的应用，充分考查了学生推理论证能力和数形结合、分类讨论、转化与化归等数学思想.第（1）问由函数的零点个数确定参数的取值范围，直接含参分类讨论与参变量分离（完全分离或部分分离）均可完成，属常规题型；第（2）问求证一个二元不等式，需要消元、巧妙构造才可简单证明，巧思妙想展示魅力.此问题实质上是证明函数极值点偏移（右偏）的问题，是一个热门问题，背景深厚，内涵丰富，要求学生具有灵活的转化与化归思想.从解题方法上看，本题强调通性通法，突出数形结合、分类讨论、转化与化归、函数与方程等数学思想.本题作为压轴题，由易到难，梯度明显，综合性强，思维方式多样，较好地考查了不同层次考生的分析问题、解决问题的能力，凸显了压轴题的选拔功用.

三、解法赏析

（一）第（1）问的解法赏析

第（1）问由函数零点个数确定参数的取值范围，我们可以采用分类讨论，结合零点存在性定理求解；也可以采用参变量分离，数形结合的方法加以解决，这两种方法都是通性通法.

解法1（含参分类讨论）：f（x）=（x-2）ex+a（x-1）2，

f′（x）=（x-1）ex+2a（x-1）=（x-1）（ex+2a）.

①设a=0，则f（x）=（x-2）ex，f（x）只有一个零点，不合题意.

②设a＞0，则当x∈（-∞，1）时，f′（x）＜0，当x∈（1，+∞）时，f′（x）＞0，

所以f（x）在（-∞，1）上单调递减，在（1，+∞）上单调递增.

又f（1）=-e，f（2）=a，取b满足b＜0且b＜ln，则

③设a＜0，由f′（x）=0，得x=1或x=ln（-2a）.

又当x≤1时，f（x）＜0，所以f（x）不存在两个零点.

点评：导函数f′（x）含有ex+2a，故以0为分界点进行讨论，讨论标准的确立是完成整个解题过程的关键，要求做到不重不漏，每种情形个个击破，分类讨论对逻辑思维能力的培养有很大好处，切忌平时嫌麻烦而一味规避分类讨论，刻意追求技巧性强的方法，弱化常规训练.

解法2（分离参数）因为f（1）≠0，所以x=1不是函数f（x）的零点，

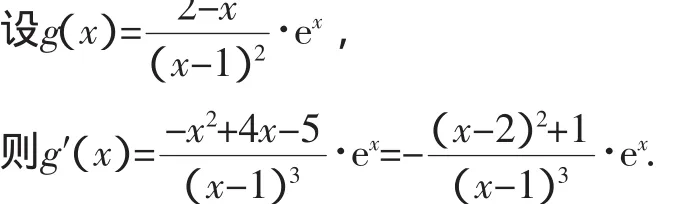
因此，当x∈（-∞，1）时，f′（x）＞0，g（x）单调递增，而当x→-∞，g（x）→0+，当x→1-，g（x）→+∞，故当x∈（-∞，1）时，g（x）∈（0，+∞）；

当x∈（1，+∞）时，g′（x）＜0，g（x）单调递减，而当x→+∞，g（x）→-∞，当x→1+，g（x）→+∞，故当x∈（1，+∞）时，g（x）∈R.

故当a＞0时，函数y=a与函数y=g（x）有两个公共点，

即方程a=g（x）有两解，此时a的取值范围为（0，+∞）.

点评：参变量分离省去了对参数的讨论，显得简单明了，对分离后所得的函数g（x）的研究用到了极限思想，帮助我们快速把握函数图像的变化趋势，对解题有很大的帮助，日常教学中应加强引导和渗透.

解法3（部分分离参数）：方程f（x）=（x-2）ex+a（x-1）2有两个零点⇔函数g（x）=（x-2）ex与函数h（x）=-a（x-1）2有两个公共点，

g′（x）=（x-1）ex，因此

当x∈（-∞，1）时，g′（x）＜0，单调递减，当x→-∞，g（x）→0-；

当x∈（1，+∞）时，g′（x）＞0，单调递增，当x→+∞，g（x）→+∞并且g（1）=-e＜0.

所以当x∈（-∞，1）时，g（x）∈（-∞，0），当x∈（1，+∞）时，g（x）∈R.

又h（x）=-a（x-1）2是以（1，0）为顶点的二次函数，

①若a=0，则g（x）与h（x）=0只有一个公共点，故a≠0；

②若a＞0，则h（x）为开口向下的抛物线，所以g（x）与h（x）有两个公共点，故a＞0；

③若a＜0，则h（x）为开口向上的抛物线，所以g（x）与h（x）不会有两个公共点（此处只能通过图像说明没有两个公共点，原因是指数函数与二次函数的递增速度不同）.

综上所述，a的取值范围为（0，+∞）.

点评：参变量部分分离是对完全分离的变通，可以灵活分配左右两端的式子结构，化归到熟悉的函数式，以达到化繁为简的解题功效.以上两种解法思路：由函数的零点⇔方程的根⇔分离为求两个函数的交点⇔函数的图象性质应用.

（二）第（2）问的解法赏析

第（2）问求证一个二元不等式，实质上是证明函数极值点偏移（右偏）问题，是一个近几年高考热门问题，背景深厚，内涵丰富.问题的解决需要学生有较高综合分析能力，巧妙利用对称性结合单调性，能够较快地分析出解题思路，从而有较好的入手点.消元是处理多元问题的常用策略，把多元问题减元或转化成一元问题时求解.本题自变量间的不等关系x1+x2＜2如何与函数联系起来呢？可逆用函数的单调性转化为函数值之间的不等关系.基于如此分析，我们可以得到下列证法：

（2）证法1：不妨设x1＜x2，由（1）知，x1∈（-∞，1），x2∈（1，+∞），2-x1∈（1，+∞），

而f（x）在（1，+∞）上单调递增，所以x1+x2＜2⇔1＜x2＜2-x1⇔

0=f（x2）＜f（2-x1），即只需证明f（2-x1）＞0.

由f（2-x1）=-x1e2-x1 +a（x1-1）2，而f（x1）=（x1-2）ex1

+a（x1-1）2=0，

可得到：f（2-x1）=-x1e2-x1 -（x1-2）ex1

.

设g（x）=-xe2-x-（x-2）ex，

则g′（x）=（x-1）（e2-x-ex）=（x-1）

所以当x＜1时，g′（x）＜0，g（x）在（-∞，1）上单调递减，又知g（1）=0，

故当x＜1时g（x）＞g（1）=0，

从而g（x1）=，f（2-x1）＞0，即有x1+x2＜2.

证法2：不妨设由（1）知，x1∈（-∞，1），x1∈（1，+∞），2-x2∈（-∞，1）.

因为f（x）在（-∞，1）上单调递减，

所以x1+x2＜2⇔x1＜2-x2＜1⇔f（x1）＞f（2-x2），

又f（x1）=f（x2），则只需证明f（x2）＞f（2-x2），

即只需证明：∀x＞1，f（x）-f（2-x）＞0，

即f（x）-f（2-x）=（x-2）ex+xe2-x＞0.

设g（x）=（2-x）ex+xe2-x，

则g′（x）=（1-x）（ex-e2-x）=（x-1）

当x＞1时，g′（x）＞0，g（x）在（1，+∞）上单调递增，所以g（x）＞g（1）=0，因此原命题得证.从而g（x1）=f（2-x1）＞0，故x1+x2＜2.

点评：我们知道，x=1是函数f（x）的极值点.因此，欲证x1+x2＜2，即＜1，也就是说，我们的问题是要证明极值点x=1在两个零点x1，x2的中点的右侧，即“极值点偏移”问题，证法1、2中的“对称化构造”是处理该问题的一般方法.

证法3：不妨设x1＜x2，由（1）知，x1∈（-∞，1），x2∈（1，+∞），2-x2∈（-∞，1）.

所以x1+x2＜2⇔x1＜2-x2＜1⇔g（x1）＜g（2-x2），

又g（x1）=g（x2），则只需证明g（x2）＜g（2-x2），

即只需证明：∀x＞1，g（x）-g（2-x）＜0，即g（x）-g（2-

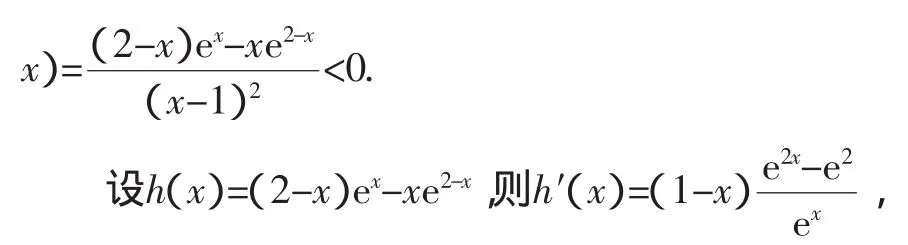
当x＞1时，h′（x）＜0，而h（1）=0，

故当x＞1时，h（x）＜h（1）=0，

从而g（x）-g（2-x）＜0，故x1+x2＜2.

点评：此法对应（1）中解法2.将两问解答连接在一起，解法就很流畅、自然.它仍然是通过问题转化，最终通过构造函数来解决问题.

证法4：不妨设x1＜x2，由（1）知，x1∈（-∞，1），x2∈（1，+∞），2-x2∈（-∞，1）.

因为f（x）在（-∞，1）上单调递减，

所以x1+x2＜2⇔x1＜2-x2＜1⇔＜f（x1）＜f（2-x2），

又f（x1）=f（x2），则只需证明f（x2）＞f（2-x2）.

令x2=1+m（m＞0），则2-x2=1-m，

问题转化为只需证明：∀m＞0，f（1+m）-f（1-m）＞0，

即f（1+m）-f（1-m）=（m-1）e1+m+（m+1）e1-m＞0.

设h（m）=（m-1）e1+m+（m+1）e1-m，则h′（m）=m（e1+m-e1-m），

当m＞0时，h′（m）＞0，而h（0）=0，故当m＞0时，h（m）＞h（0）=0，

从而f（x2）-f（2-x2）＞0，故x1+x2＜2.

点评：此解法与前面的1、2本质是一样的，只是后面引入m＞0，构造对称函数，利用其单调性质证明.“极值点偏移”的处理方法：①求出函数f（x）的极值点x0，②构造一元差函数F（x）=f（x0+x）-f（x0-x），③确定F（x）的单调性，④结合F（0）=0判断F（x）的符号，从而确定f（x0+x）与f（x0-x）的大小关系.

由于此类题涉及的知识面较综合，变量较多，但题意简单，学生一般审题不透彻，很难有效解答.通过对本题的多种解法分析，面对此类题需要先厘清解题脉络，找准切入口，果断分离参数和消元，将复杂问题层层转化为熟悉易懂的，争取多踩得分点，实现分数最大化.

作为教师，在平时的教育教学中，需要加强数学思想方法的渗透，如数形结合、分类讨论、转化与化归等思想，将基本的知识变化出来，基础的知识灵活出来，重点的知识反复出来，明显的知识隐蔽出来，易混淆的知识对比出来，相似的知识联想出来的思想意识.在平时解题训练中注重提炼通性通法，熟练掌握数学模式题的通用解法，在复习时要更多地注重“一题多变”、“一题多用”和“多题归一”，更多地注重思考题目的“核心”是什么，从题目中“提炼”反映数学本质的东西，掌握好数学模式题的通用方法，最终提高学生思维素质.