为学习设计教学：教学设计最根本的着力点*——以“函数的概念”的教学设计为例

☉江苏省盐城中学　刘海滨

为学习设计教学：教学设计最根本的着力点*——以“函数的概念”的教学设计为例

☉江苏省盐城中学刘海滨

一、教材分析

函数概念是中学数学中最重要的核心概念之一，函数的思想和方法贯穿高中数学课程的始终，学会用函数的观点和方法解决数学问题，是高中数学主要的学习任务之一.然而，函数概念因其取元的任意性、成象的唯一性及对应法则“f”的高度抽象性，而成为最难把握的概念之一，无论是教师的教还是学生的学，都存在很大困难.因此，如何全面而深刻地理解函数概念、破解概念教学难点是学好函数概念的根本所在.

从教的角度看，函数概念教学的核心是引导学生开展概括活动：将凝结在数学概念中的数学思维活动打开，以若干典型具体事例为载体，引导学生展开分析各事例的属性、抽象概括共同本质属性、归纳得出数学概念等思维活动而获得概念.数学教学要“讲背景，讲思想，讲应用”，概念教学则要强调让学生经历概念的概括过程.

从学的角度看，概念形成和概念同化是两种基本的概念获得方式.概念形成的实质是抽象出一类对象的共同本质属性的过程，其思维活动的核心是概括；概念同化就是学生利用已有认知结构中的相关知识理解新概念，理解的过程是新旧知识的相互作用过程，是将新知识纳入已有认知结构的过程，思维活动的核心仍是概括.

二、教学流程

1.复习回顾，点击课题

教师：在初中，我们是如何定义函数的？学习了哪些函数？

学生：对于一个变化过程中的两个变量x，y，若对于任意一个值x，都有唯一值y与之对应，则称y是x的函数，其中x叫作自变量.学过了正比例函数、反比例函数、一次函数、二次函数.

设计意图：通过举例回顾，强调“单值对应”，思考题是为了激发学生的学习动机.

2.探索实例，建构模型

教师：今天我们来进一步从其他角度学习函数的概念.（板书课题）

实例一：一枚炮弹发射后，经过26s落到地面击中目标.炮弹的射高为845m，且炮弹距地面的高度h（单位：m）随时间t（单位：s）变化的规律是h=130t-5t2.

问题1：炮弹飞行1s，5s，13s，30s时离地面的高度？

问题2：变量t和h的取值范围是多少？用集合表示.

问题3：对于数集A的任意一个时间t，按照变化规律，在数集B中是否都有唯一确定的高度h和它对应.

实例二：图1中的曲线显示了南极上空臭氧层空洞的面积从1979～2001年的变化情况.

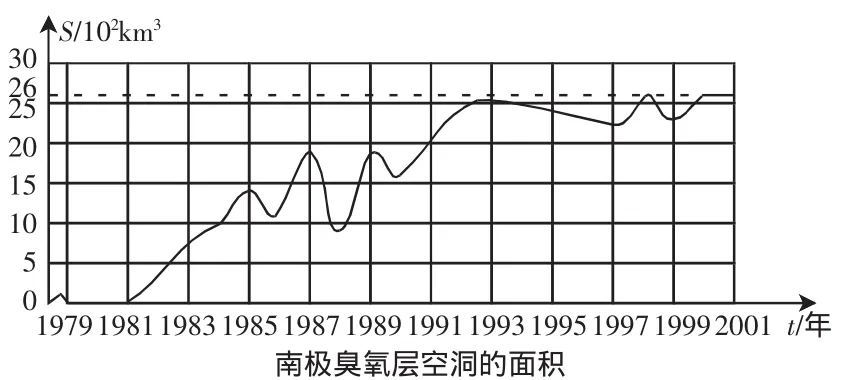
图1　

问题4：曲线中，哪一年空洞面积S最大？S=1500万平方千米的年份有哪些？

问题5：t和S的取值范围是什么？用集合表示.

问题6：对于数集A中的每一个时刻t，按照曲线，在数集B中是否都有唯一确定的臭氧层空洞面积S和它对应.

实例三：表中恩格尔系数随时间（年）变化的情况表明，“八五”计划以来，我国城镇居民的生活质量发生了显著变化.

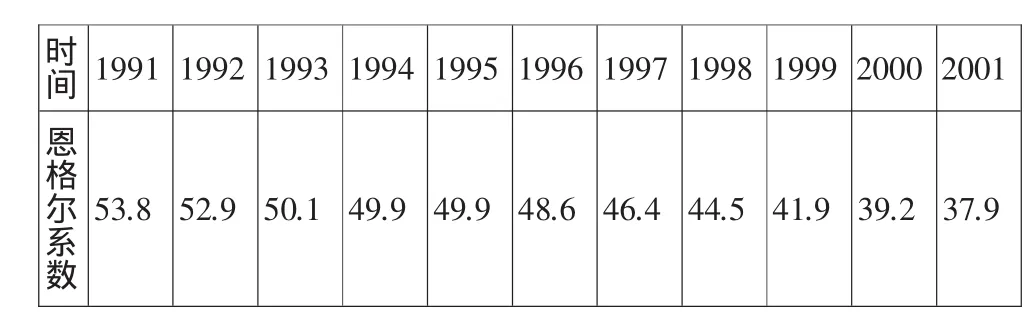
时间1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001恩格尔系数53.852.950.149.949.948.646.444.541.939.237.9

问题7：系数y与时间x之间的关系是否和前面两例中的变量之间的关系相似？

问题8：仿照前面两个实例来描述这个关系？

设计意图：进一步体会函数是两个变量之间的函数模型.

3.归纳共性，形成概念

教师：以上三个实例有什么共同点？

学生：在集合A中每取一个数，按照一定的对应关系，在集合B中都有唯一的一个数与之对应.

教师：如果我们把A中的数记为x，集合B中的数记为y，对应关系记为f，那么我们又如何归纳上述三个例子的共同特征呢？

学生：对于数集A中的每一个x，按照某种对应关系f，在数集B中都有唯一确定的y和它对应.

教师补充：像这样在对应关系f作用下集合A到集合B，我们记作：f：A→B，读作：f，A到B.为此我们得到函数的概念：设A、B是非空数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f（x）和它对应，那么称f：A→B为从集合A到集合B的一个函数（function），记作：y=f（x），x∈A.其中，x叫自变量，x的取值范围A叫作定义域（domain），与x值对应的y值叫函数值，函数值的集合C=｛f（x）|x∈A｝叫值域（range）.

教师：对于函数定义中的“f（x）”，我们该如何理解呢？可否理解成f与x的乘积呢？

学生活动（分组讨论，代表回答）：f（x）只是表示函数符号，是集合A中取x时，按对应关系f，在集合B中的值.不能理解成f与x的乘积.

设计意图：三个对应关系不同引导学生引进符号表示，体会对应关系在刻画函数概念中的作用.

4.辨析概念，深化巩固

教师：f（x）是否可以换成其他符号呢？

学生：因为f（x）只表示函数符号，f是表示对应关系的字母，也可用其他字母表示，如g表示对应关系，则g（x）就表示在集合A中取x时，按对应关系在集合B中的值.

学生（一名突然举手的学生）：老师，“对应关系”是什么意思？

教师：通过前面实例，我们不妨可以这样理解：把f看成一台加工的机器，集合A是原料箱，集合B是产品箱，集合A中每给一个原料经过f机器加工就成B中的一件产品.例如h与变量t满足的关系式h=130t-5t2，t每取一个值，按照这种对应关系，h都有唯一对应的值.

例1你能说说已学函数的定义域和值域吗？（师生共同完成）

①一次函数f（x）=ax+b（a≠0）：定义域为R，值域为R；

②反比例函数（k≠0）：定义域为｛x|x≠0｝，值域为｛x|x≠0｝；

③二次函数f（x）=ax2+bx+c（a≠0）：定义域为R，值域：当a>0时

注：（1）函数的定义域通常由问题的实际背景确定，如我们刚开始所述的三个实例.如果只给出解析式y= f（x），而没有指明它的定义域，那么函数的定义域就是指能使这个式子有意义的自变量的取值集合.（2）函数的定义域和值域用集合表示.

例2（幻灯片展示）下列哪些表示集合A到集合B的函数？若不是，说明理由.

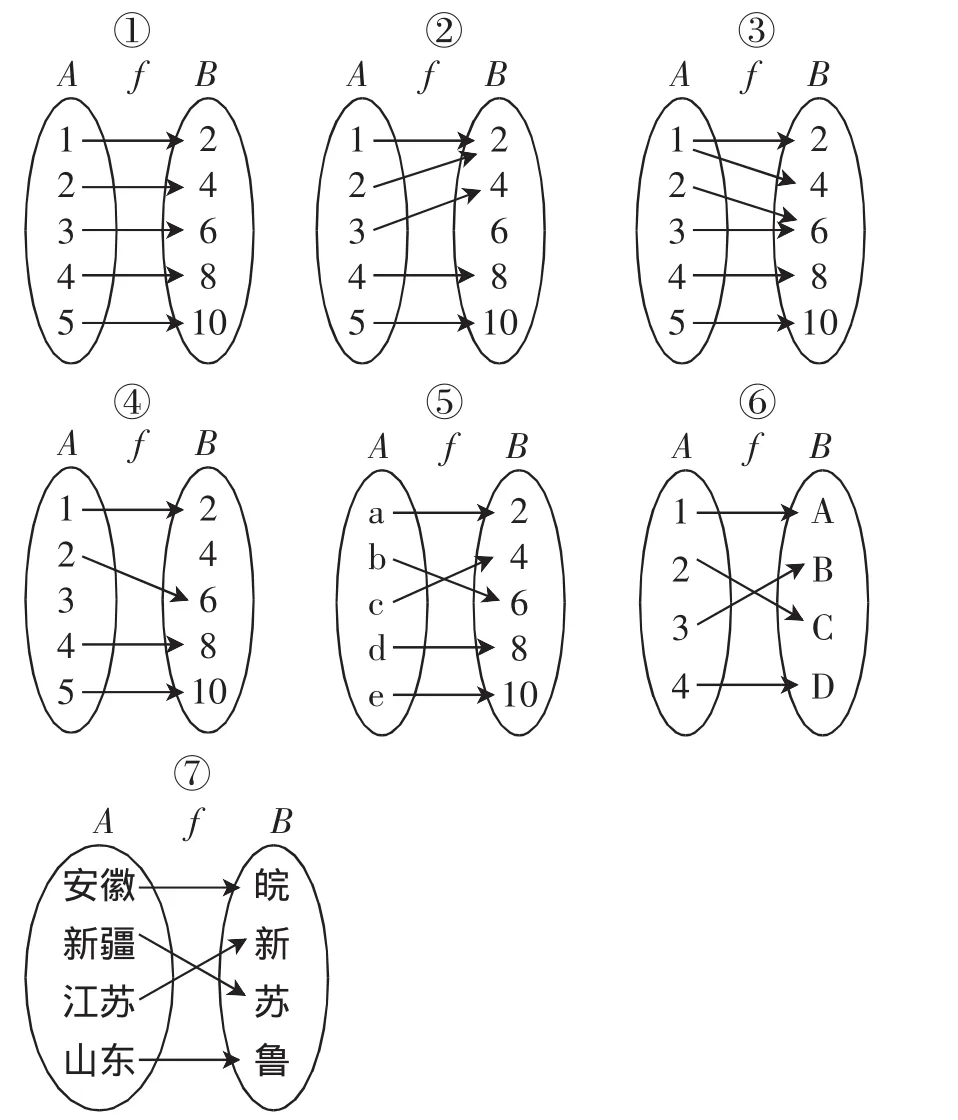
学生1：①是；②也是函数.

教师追问：②为什么是函数呢？在集合A中没有数与集合B中的6对应呀？

学生1迟疑后回答：因为函数的定义是如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数和它对应.本题满足函数的定义.

教师追问：也就是说集合B中可以有元素剩余了？

学生1：是.

教师借此机会把刚才板书的函数定义中“值域是集合B的子集”进行解释.

教师强调：像①中的对应关系，我们就可以理解为集合A中数的2倍等于集合B中的数；②中也存在着一种对应关系，只是我们找不出具体的对应关系的式子.

学生2：③④都不能表示函数关系；因为③的A集合中的数1在集合B中有2与4两个数与之对应，不满足函数定义；④的A集合中的数3在集合B中没有数与之对应，不满足函数定义.

教师：很好.所以在刚才给出函数定义时，自变量的取值集合就是A，我们称作函数的定义域.⑤⑥⑦找一名同学回答.

学生3：都是（教师疑惑）

学生4：⑤⑥是，⑦不是.

教师：为什么？

学生4：因为⑦的两个集合中元素都是省名和省的简称，故不满足函数概念.

教师提出：不错，基本上说到实质上了.⑤⑥是吗？判断是否为函数关系，主要看是否满足函数定义.

学生5（在大家纷纷议论一会后举手回答）：⑤⑥⑦都不是，因为函数定义中说A、B集合的元素必须是数，而⑤中集合A、⑥中集合B的元素都是字母，⑦中集合的元素都不是数.

教师：太棒了！（示意全班学生为学生5鼓掌）.请同学们再来看一下思考辨析，进一步来巩固函数的概念.

设计意图：用任意性和唯一性判断，找对应法则，分析定义域值域，小结：从集合A到集合B的对应关系可以是一对一、多对一，不能是一对多.函数概念的核心本质：两个数集A、B之间的一种单值对应关系：从自变量x的集合A到函数值y的集合C的一种对应关系.对于A中的任意一个元素，B中都有唯一的元素与之对应，即一对一、多对一；而B中的元素在A中的对应元素可以不唯一，也可以没有，显然B包含值域C，原因是：函数的三要素中值域是由定义域和对应关系决定的.

例3辨析下面语句的正误.

（1）y=1（x∈R）是函数吗？

学生：（1）是；（2）不是，因为当x=1时，y有两个值；（3）是.

教师：若（3）是，请大家求一下它的定义域.（板书提示：由x-3≥0且1-x≥0来求x的取值集合）.

学生：空集.

教师追问：这样还能是函数吗？

学生：不能，因为函数定义中说A、B是两个非空数集.

教师：这个问题大家终于看出来了.通过以上例子，大家讨论一下，我们从中总结函数定义具有哪些特点？

学生回答不同情况以后，教师与学生共同总结，函数定义有以下特点：①A、B必须是非空数集（若是空集就没有研究意义）；②集合A中不能有元素剩余，集合B中可以有元素剩余；③按对应关系只能一对一或多对一，但不能一对多；④集合A是函数的定义域，集合B包含函数的值域（或称函数的值域是集合B的子集）；⑤f（x）表示每给一个自变量x，按照对应关系f，都对应确定一个函数值f（x），而不是f与x的乘积.

教师：函数的概念主要由哪几部分构成？

学生：定义域、对应关系和值域.

教师：很好.我们把定义域、对应关系和值域称为函数的三要素.

（1）求函数的定义域；

（3）当a>0时，求f（a），f（a-1）的值.

（学生板演，教师点评，具体解答略）

5.课堂小结，知识提炼

今天我们收获是什么？（学生回答，教师点评）

（1）你对“函数是描述变量之间的依赖关系的数学模型”这句话有什么体会？

（2）对比初中和高中函数概念，你有什么发现？

设计意图：反馈学生的当堂表现，了解知识掌握情况.

三、结束语

函数概念已成为现代数学的基本思想之一，是整个高中数学的核心概念，它渗透到了数学的一切领域.函数是数学知识体系的有力基础，也是数学学习中最难掌握的概念之一.

数学发展史表明，函数概念从产生到完善，经历了漫长而曲折的过程.这不但因为函数概念系统复杂、涉及因素众多，更重要的是伴随着函数概念的不断发展，数学思维方式也发生了重要转折：思维从静止走向了运动、从离散走向了连续、从运算转向了关系，实现了数与形的有机结合，在符号语言与图、表语言之间可以灵活转换.在函数的研究中，思维超越了形式逻辑的界限，进入了辩证逻辑思维.与常量数学相比，函数概念的抽象性更强、形式化程度更高.总之，概念的识别优于概念特征的说明，概念外延的掌握优于概念内涵的掌握.对概念内涵的掌握，取决于概念本质特征的多少及它们之间的关系.本质属性越多越鲜明，概念形成越容易；非本质属性越多越明显，概念形成越难.对于所有概念，都是先掌握具体概念后掌握抽象概念，先掌握形式概念后掌握辩证概念.

*本文是江苏省中小学教学研究室第九期课题《基于数学实验室建构的高中数学实验教学模式的研究》（编号：Jk9-L157）的研究成果之一.