高中数学恒成立与存在性问题的探究
吴吉云
(山西省吕梁市离石区江阴高级中学)
高中数学恒成立与存在性问题的探究
吴吉云
(山西省吕梁市离石区江阴高级中学)
恒成立与存在性问题是高中数学中常见的一种题型,基于学生的认知水平对这种题型的理解比较吃力,特别是一题中恒成立与存在性问题同时出现时,学生更不容易把已知条件演绎出来,针对这一困惑点,通过对一道题的多种变式讲解,让学生对这类问题的认识更上一层楼.
恒成立;任意的;存在;参变分离
一、存在性问题
例1.函数(fx)=4x2-8x+2,存在x∈[1,2],使(fx)>2x+m成立,求m的取值范围.
解:因为存在x∈[1,2],使(fx)>2x+m成立.
所以存在x∈[1,2],使(fx)-2x>m成立,即:((fx)-2x)max>m.
令g(x)=(fx)-2x=4x2-10x+2,x∈[1,2],
小结:(1)存在x∈[a,b],使(fx)>m成立⇔(fx)max>m;
(2)存在x∈[a,b],使(fx)<m成立⇔(fx)min<m.
二、恒成立问题
变式1:函数(fx)=4x2-8x+2,对任意的x∈[1,2],使(fx)>2x+m恒成立,求m的取值范围.
解:因为对任意的x∈[1,2],使(fx)>2x+m成立.
所以任意的x∈[1,2],使(fx)-2x>m成立,即:((fx)-2x)min>m.
令g(x)=(fx)-2x=4x2-10x+2,x∈[1,2],
小结:(1)对任意的x∈[a,b],使(fx)>m成立⇔(fx)min>m;
(2)对任意的x∈[a,b],使(fx)<m成立⇔(fx)max<m.
变式2:设函数(fx)=4x2-8x+2,对任意的x∈[1,)∪(,2],使(fx)>2x+m成立,求m的取值范围.
令g(x)=(fx)-2x=4x2-10x+2,x∈[1,)∪(,2],
(2)恒成立、存在性问题中,当参变分离后构造出的新函数,求新函数的最值时,当最值取不到时,要考虑m取值范围中“=”的取舍.
例2.设函数(fx)=x ln x-a,函数(fx)<0在(0,)上恒成立,求
a的取值范围.
当x=0时g(x)取最大值,但此时g(x)无意义.所以用洛必达法则求解.
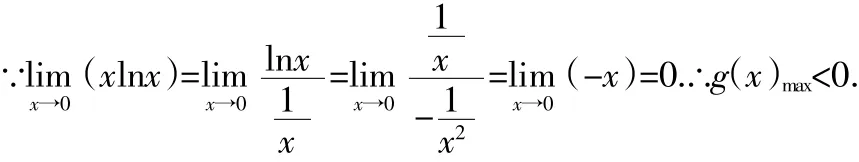
∴a≥0
小结:此题中g(x)在x=0时取最大值,但g(x)在x=0处无意义,所以用洛必达法则求解(极限思想).
三、结语
解决恒成立与存在性问题首选参变分离,参变分离后都可以转化为求构造出的新函数的最值问题,在求新函数的最值时有三种情况:(1)在定义域内最值存在(如例1和变式1);(2)在定义域内最值不存在,但在定义域端点值处取最值并且在该点处有意义(如变式2),此时可以借助端点值所对应的函数值求参数的取值(注意参数端点值的取舍);(3)在定义域内最值不存在,但在定义域端点值处取最值并且在该点处无意义(如例2),此时可以用洛必达法则解决.
[1]佟成军,冯善状.一道试题讲评的“幕后台前”[J].中学数学教学参考(上旬),2013(6):17-20.
[2]张良超.高三解题:想得好才能做好[J].中学数学教学参考(上旬),2012(10):27-29.
·编辑张慧

