粗糙元诱导的高超声速边界层转捩

段志伟， 肖志祥

清华大学 航天航空学院， 北京　100084



粗糙元诱导的高超声速边界层转捩

段志伟， 肖志祥*

清华大学 航天航空学院， 北京100084

基于有限体积方法，直接数值模拟了高超声速边界层内不同形状粗糙元导致的强制转捩现象；为了能够深入探究强制转捩机理，解析小尺度运动，同时又能够较好地捕捉激波，采用高阶色散最小耗散可调(MDCD)格式对Navier-Stokes方程组对流项进行重构。计算结果表明，数值结果与对应的实验值吻合较好；该方法能解析小尺度的流动结构以及规则结构的破碎与失稳过程，可揭示粗糙元引起的强制转捩机理，即此类强制转捩主要由粗糙元顶部的三维剪切层失稳导致。对多种粗糙元的转捩效果进行了定量研究，影响因素包括粗糙元形状、几何参数等。

高超声速； 粗糙元； 边界层转捩； 参数化影响； 直接数值模拟

在高超声速飞行器绕流中，边界层转捩是非常重要的流动现象。它主要影响飞行器的摩擦阻力、气动加热、进气道质量捕获、发动机内燃料掺混和燃烧等[1]。粗糙元可以改变边界层基本流动剖面，甚至产生较大扰动，对边界层流动的转捩产生较大影响；由于粗糙元改变了流动状态，其自身也面临比较严峻的气动热环境等。粗糙元诱导转捩的影响因素非常多，对其转捩机理与具体效果的研究尚未十分明确，是目前国际上的研究热点之一。因此本文针对粗糙元形状、几何参数等，对其诱导转捩的效果进行了定量研究。

大多数情况下，粗糙元会促使转捩提前，并且随着粗糙元高度的增加，其促进转捩效果会更明显。早在20世纪60年代， Van Driest等[2]对粗糙元在马赫数Ma=2.71的超声速边界流动中进行了触发转捩研究，通过大量的试验数据拟合得到转捩位置与单位雷诺数的关系曲线，他们发现粗糙元存在着“临界高度”与“有效高度”。虽然该试验是在常规风洞内进行，风洞噪声比较大，所获得的转捩曲线与实际情况稍有差别，但是转捩趋势相同，该试验对后续的粗糙元研究有极大的启发意义。在近期的风洞试验中，赵慧勇等[3]也发现了粗糙元的“临界高度”和“有效高度”，有效高度大约为边界层厚度的0.7～0.8倍。

粗糙元高度是影响其转捩的重要因素之一。当然，马赫数、雷诺数、来流湍流度、粗糙元形状等对转捩效果也有较大影响。试验研究表明转捩雷诺数随马赫数增加而增加[4]，这可能与高马赫数对剪切层的稳定作用有关。即便在粗糙元足够高时，来流湍流度对转捩效果仍然有很大影响。Casper等[5]的静音风洞试验表明，在静音条件下的转捩距离比噪声条件下增长了一倍左右。

粗糙元的形状不仅影响转捩效果，同时对流场中的扰动产生、气动力热环境等也有着较大影响。理想的粗糙元应该能够很快触发转捩，并且对流场的扰动要尽量小，同时自身不产生过大的阻力和热流，尤其在粗糙元上的热流不至于过大，否则易烧毁。因此，关于粗糙元形状对转捩的影响研究由来已久。

一般来说，对于高超声速边界层转捩，三维粗糙元效果要优于二维粗糙元[6]。对于不同形状的三维粗糙元，其有着类似的流动拓扑结构：在粗糙元上游会形成几对反转的涡，在正后方形成不稳定尾迹涡和侧边的马蹄涡(或次涡)结构[7-13]。如Danehy等[11]采用一氧化氮平面激光可视技术显示了详细的尾迹涡结构随着粗糙元钝度增加，其上游分离涡与表面之间的距离也增大，转捩效果更加明显。当然综合考虑转捩效果和其对流场的影响后，斜坡形单元可能是比较好的选择[8]。

风洞试验可以研究粗糙单元转捩，但是由于受到显示技术的限制，其给出的流动数据较少。随着计算机技术的发展，大规模的数值计算已成为可能。采用数值计算方法可以给出风洞试验所不能观测到的更丰富的流动结构，近年来很多学者对粗糙元导致的高超声速边界层转捩进行了数值模拟。Bernardini等[14]的数值计算表明，当雷诺数足够高时，在所有马赫数工况下(0，0.25，1.1，2，3，4)粗糙元尾迹区都会出现不稳定的发卡涡结构，而这正是充分发展湍流的显著特征之一。他们的计算结果表明，压缩性对流动结构的影响并不明显。虽然压缩性对尾迹区的流动结构影响不大，但是在高超声速工况下，当粗糙元的高度超过声速线时，粗糙元上游会形成明显的脱体激波，其前方的分离泡也会导致分离激波的出现。Bartkowicz等[15]的计算结果清晰地展示了粗糙元前的激波与涡结构；粗糙元前的分离涡随主流向下游发展形成了极强的马蹄涡和尾迹涡结构。这些数值模拟结果与风洞试验[10]所展示的流场结构几乎完全相同。

对于粗糙元促进高超声速边界层转捩的研究已经持续超过了50年，而且多种形式的粗糙元也已经被成功应用到高超声速飞行器上，但是对于其促进转捩的机理却一直没有统一完整的解释。 Schneider[4]在他的综述性文章中将粗糙元的作用总结为：① 粗糙元会在尾迹区产生流向涡结构和不稳定的剪切层。当粗糙元大于“有效高度”后，转捩会在下游立即发生；当其尺寸较小时，转捩距离可能会在更下游位置发生，尾迹失稳可能是由剪切层失稳或者尾迹涡失稳主导的。② 当粗糙元尺寸较小时(基于粗糙元高度h的雷诺数Reh<10)，粗糙元后的流向涡可能通过一些失稳机制发展，例如横流、Görtler涡或者瞬态增长等。③ 粗糙元也可能通过感受性机理，与声波或者其他的来流扰动相互作用进而发展出失稳波。

对于大尺寸的粗糙元，Iyer和Mahesh[16]对平板上的单个半球形粗糙元进行了研究。他们对这种孤立式的粗糙元转捩机理进行了定性描述：由于粗糙元的存在，边界层内会产生三维的流动分离，进而会形成剪切层和涡结构；在粗糙元下游，不稳定的反转涡结构会不断冲击剪切层从而形成发卡涡。Muppidi和 Mahesh[17]对来流马赫数2.9的平板上的分布式粗糙元进行了直接数值模拟(DNS)，他们认为尾迹涡上洗作用会促使流向涡结构与剪切层不断相互作用，从而导致边界层转捩。

Tullio等[18]综合应用DNS、三维稳定性方程(Three Dimensional Parabolized Stability Equation, PSE-3D)和二维全局稳定性(BiGlobal Stability)方法研究了孤立的长方体粗糙元导致的超声速平板边界层转捩问题，来流马赫数为2.5。他们认为粗糙元诱导转捩是整个三维剪切层不稳定性的结果而不是传统的K-H不稳定性。他们发现粗糙元改变了基本流的分布，从而导致流动稳定性的极大改变，而其中最重要的因素就是尾迹中的反转涡对将物面附近的低能流体抬升。

虽然对强制转捩机理存在着多种理论解释，但多数人认为，粗糙元对基本流的改变以及其自身提供的扰动在转捩中占据主导作用。在众多影响强制转捩效果的因素中，粗糙元的高度是最重要的参数之一，对其研究也较为透彻；粗糙元的几何外形对转捩效果也有较大的影响，目前研究相对较少。

评价粗糙元诱导的转捩，必须综合考虑其转捩效果及其带来的气动热、气动力增量。因此本文着重针对粗糙元的几何外形对转捩的影响进行系统研究，给出各参数的定量影响，为工程应用提供指导。具体来说，是利用实验室开发的三维Navier-Stokes方程求解程序UNITs (Unsteady Navier-Stokes solver)，采用高精度的数值方法，对粗糙元诱导的高超声速边界层转捩进行了直接数值模拟研究。

1　数值方法

本文采用基于有限体积方法的DNS求解Navier-Stokes方程。对流项采用任玉新等[19-20]发展的色散最小耗散可调(MDCD)格式进行重构，该格式可以对色散和耗散特性分别进行控制，在保证色散最小的前提下，优化耗散特性。

MDCD格式的基本思路为，采用P个模板点进行数值重构时，最多可得到P阶精度结果。如果降低精度为P-2阶，则可得到2个自由参数。这2个自由参数分别对应了格式的色散特性和耗散特性，即可对该格式的色散和耗散分别进行优化控制。MDCD为线性重构格式，为了能够计算高超声速流动，将其与加权紧致非线性(WENO)格式进行耦合，在流动间断处采用WENO格式，而在光滑流场采用MDCD格式，即构成了MDCD-WENO格式。具体过程可见文献[19-20]。

具体来说，本文采用了4阶MDCD-WENO格式。其最小耗散可等于零，即与6阶中心格式相同；最大耗散则要大于传统WENO格式。在耗散特性不变的基础上，其色散特性同样进行了优化，达到了该格式的理论最小值。

MDCD-WENO格式重构已经成功应用于直接数值模拟粗糙元触发边界层转捩的问题，计算结果和试验吻合较好[21-22]。

另外，采用隐式上下分解对称高斯赛德尔伪时间推进 (Lower-Upper Symmetric-Gauss-Seidel pseudo Time Sub-iteration， LU-SGS-TST)方法进行时间推进。全局统一时间步长(无量纲时间t=1×10-5)以获得非定常流动特征，通过消息传递界面 (Message Passing Interface， MPI)实现并行计算。

2　模型验证

计算模型是一个高h=10.2 mm，直径D=5.97 mm的圆柱。该试验由Wheaton和Schneider[23]在普渡大学的静音风洞中进行，风洞直径Dt=240 mm。当流场中没有粗糙元时，该处的边界层厚度约为8.3 mm。数值计算中，自由来流马赫数Ma=6，雷诺数Re=6.657×107m-1，来流温度T∞=53 K， 壁面温度Tw=300 K。三维计算网格总数约为1亿，粗糙元尾迹区的网格在流向和展向几乎各向同性，尺度为0.4 mm，网格距壁面的最小距离为20 μm。计算域为粗糙元上游15D处至下游66D处。

计算的流场相干结构如图1所示，用Q的等值面表示，并以无量纲速度u/U∞着色。本文的计算结果与Bartkowicz等[15,24]的结果相近。

图1　流场中的相干结构(以速度着色的Q等值面表示)Fig.1　Coherent structures showed by Q contour surface (colored by velocity)

风洞试验中在粗糙元上游1.5D处的风洞壁面布置了脉动压力传感器，观测到粗糙元的存在会造成主频率约为21 kHz的压力脉动，而在数值计算中获得的主频为19.23 kHz，如图 2所示。Bartkowicz等[15,24]对同样算例采用2.7亿网格进行了数值模拟，其计算的频率约为18 kHz。图中纵坐标为归一化压力脉动F。

图2　试验和计算的压力脉动频谱Fig.2　Frequency spectrum of pressure fluctuation in test and calculation

3　研究结果及讨论

3.1不同形状粗糙元诱导转捩的效果

计算模型为3种不同形状的粗糙元，基准流动为平板边界层流动。粗糙元的形状如图 3所示，对于斜坡形粗糙元，其底边长d1=3.2 mm，高度h与当地的边界层厚度基本相同，为0.8 mm，斜坡角θ=100；钻石形粗糙元的对角线长度d2=3.2 mm，圆柱形粗糙元的直径d3=3.2 mm，其高度与斜坡高度相同，同为0.8 mm。粗糙元距平板前缘Lu=60 mm。在数值计算中，将粗糙元下游长度Ld设为100 mm，平板宽度Wp设为34.1 mm，如图3所示。

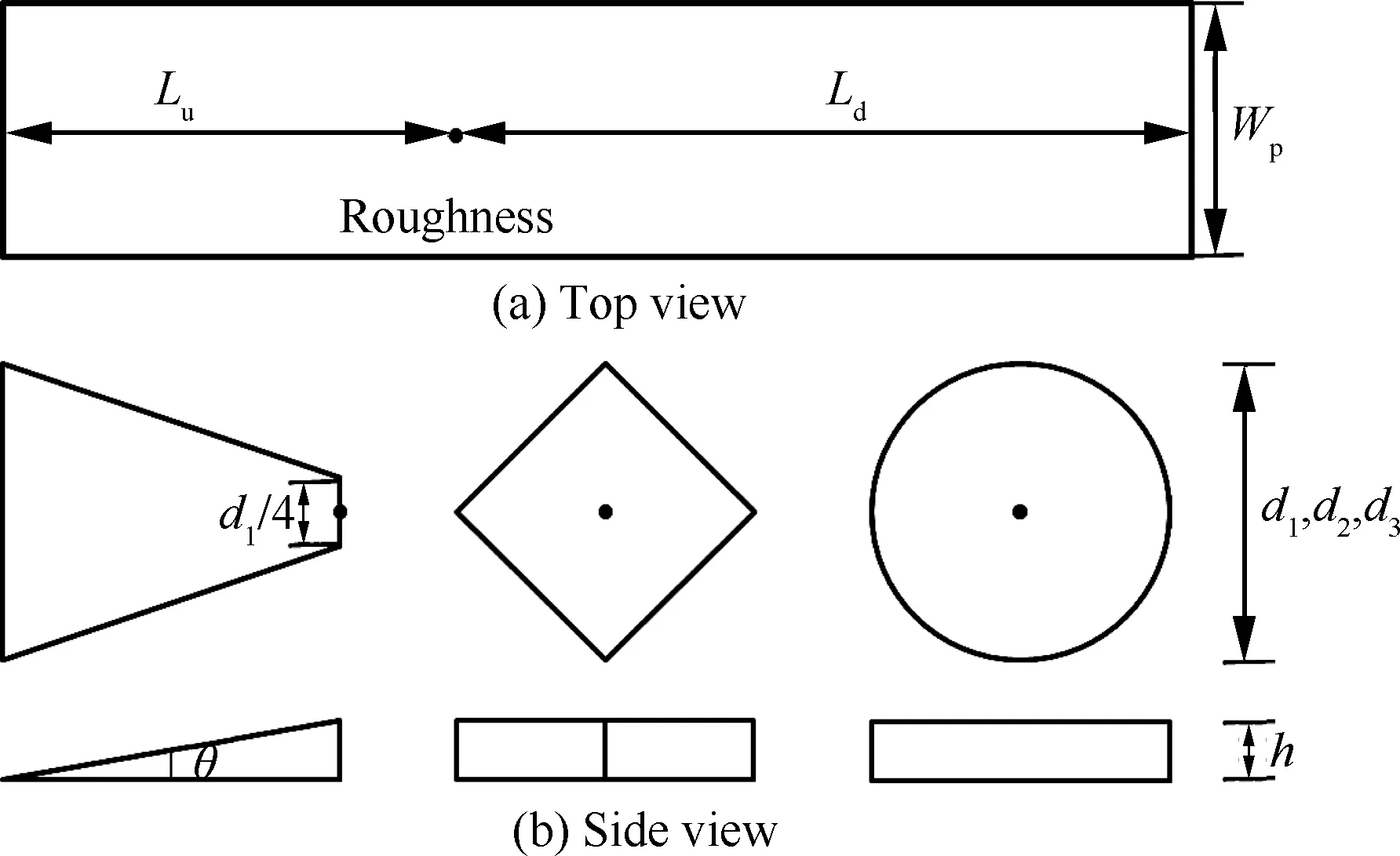
图3　计算模型Fig.3　Calculation model

Tirtey等[10]在冯·卡门研究所(Von Karman Institute, VKI)的高超声速风洞中进行了该试验。根据试验数据，来流马赫数为6，雷诺数为2.6×107m-1，来流温度约为70 K，物面设为等温壁面，温度为300 K。

本文研究的斜坡形、钻石形和圆柱形粗糙元的高度和宽度都相同，但是转捩效果却有较大的差别。图 4给出了距离平板0.4 mm(0.5h)处的温度T分布云图，在粗糙元尾迹区，可以看到极强的剪切层和流向涡结构，随着流动向下游发展，流向涡逐渐扭曲形成规则的涡结构，在更下游接近出口处，流动结构变得更加复杂无序，流动转捩为湍流。

对于斜坡形粗糙元，其马蹄涡很弱，尾迹集中在较窄的范围内；对于钻石形和圆柱形粗糙元，除了在其正后方的流动区域内形成尾迹涡，在展向较远距离处，会形成极强的马蹄涡。钻石形粗糙元的马蹄涡比较稳定，在计算域内没有失稳；而圆柱粗糙元的马蹄涡更加不稳定，在其下游20 mm处就形成了规则的涡结构，在下游60 mm处与尾迹涡纠缠在一起，流动转捩为湍流。

图4　距平板0.4 mm处的温度分布云图Fig.4　Temperature distribution contour on y=0.4 mm plane

图5给出了粗糙元附近的压力脉动频谱。压力样本点分别位于粗糙元上下游分离泡的起始位置附近。对于斜坡形单元，其上游压力样本点位置为(-4.5,0,0) mm，下游位置为(2.3,0,0) mm；对于钻石形和圆柱形粗糙元，上下游压力样本点位置分别为(-2.4,0,0) mm和(3.4,0,0) mm。斜坡形粗糙元的不稳定分离泡脉动主频为55.27 kHz，同时还存在着明显的谐频(110.54, 165.82，221.09 kHz等)，而钻石形和圆柱形粗糙元的脉动主频则分别为30.19 kHz和42.58 kHz，没有明显的谐频出现。 圆柱形粗糙元的脉动能量最高，钻石形粗糙元次之，斜坡形粗糙元的脉动能量最低。

图5　粗糙元上游和下游位置处的压力脉动频谱Fig.5　Frequency spectrum of pressure fluctuationbefore and after roughness elements

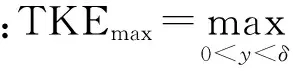
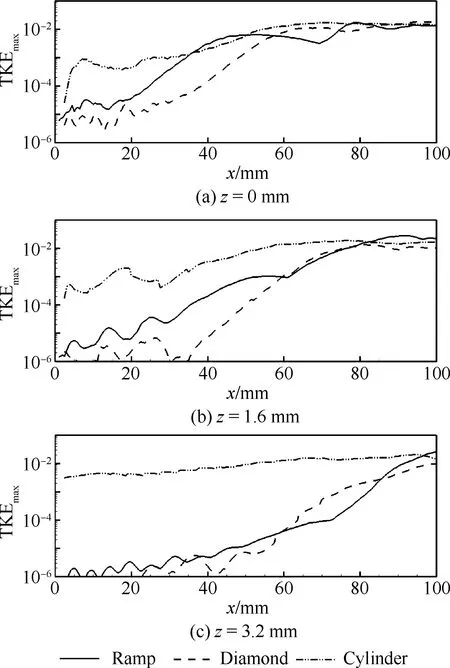
图6　不同展向位置截面的最大湍动能分布Fig.6　Maximum TKE distribution on different streamwise cross-section planes

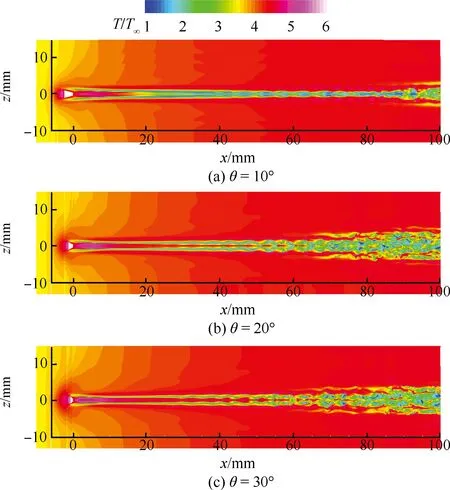
在对称面位置(z/d=0)处，在0 mm

在x>40 mm之后，扰动增长速度逐渐下降，之后TKEmax达到峰值，意味着湍动能达到饱和状态。在此区间范围，扰动经历了非线性失稳和“breakdown”过程。通常扰动在“breakdown”之后流动迅速转捩为湍流，因此本文以扰动达到峰值位置为转捩位置，下文将对此进行比较。

斜坡形粗糙元在x≈80 mm处扰动达到峰值，即发生转捩，而钻石形和圆柱形的转捩位置为x≈70 mm。

在z/d=0.5和1.0位置处，圆柱形粗糙元的TKEmax均能到达峰值，说明在这些位置其尾迹都发生了转捩；而斜坡形和钻石形粗糙元在这些位置处没有发生转捩。这和图 4中的瞬时温度分布情况一致。

图7给出了平板上的无量纲热流斯坦顿数St分布，可以看到斜坡形的尾迹最窄，而圆柱形粗糙元的尾迹最宽，与之前的分析一致。

图7　平板的无量纲热流分布Fig.7　Normalized heat flux distribution on wall surface

粗糙元附近的无量纲热流分布如图8所示，圆柱粗糙元的头激波强度最大，波后温度最高(见图4)，因此壁面热流最大；而斜坡形粗糙元的头激波最弱，其相应的壁面热流也最低；钻石形粗糙元的热流居中。另外，由于圆柱形和钻石形粗糙元的钝度较大，其上游会形成马蹄涡，在壁面上则表现为粗糙元周围的高热流条带；当前的斜坡形粗糙元则没有形成明显的马蹄涡结构。

表1给出了不同粗糙元引起的最大热流Hmax及其位置分布。对于斜坡形粗糙元，其最大热流在粗糙元的顶点位置(即粗糙元最高处的中点位置)，其热流最大值约为该处层流热流Hlam的16.7倍；钻石形粗糙元的最大热流在迎风顶点处，约为层流的133.7倍；圆柱形粗糙元的最大热流位置与钻石形粗糙元相同，其约为层流的173.8倍。

图8　粗糙元附近的无量纲热流分布Fig.8　Normalized heat flux distribution near roughness elements

表1　粗糙元引起的最大热流及位置

Table 1Maximum heat flux caused by roughness element and its location

TypeHmaxHmax/HlamLocationRamp4.10616.691VertexDiamond32.888133.691WindwardvertexCylinder42.753173.793Windwardvertex

计算结果表明，粗糙元尾迹区内的三维剪切层失稳是流动转捩的主要原因。对于不同形状的粗糙元，斜坡形的湍流尾迹最窄，圆柱形的湍流尾迹最宽；钻石形和圆柱形粗糙元下游的转捩位置更靠前，斜坡形的转捩位置稍微靠后。

另一方面，钻石形和圆柱形粗糙元引起的热流峰值远高于斜坡形粗糙元的热流峰值；钻石形粗糙元的热流峰值稍小于圆柱形。综合转捩效果与引起的热流峰值来看，斜坡形粗糙元可以作为较好的转捩触发装置。

3.2斜坡形粗糙元对诱导转捩的参数化

3.2.1斜坡角度

斜坡形粗糙元的宽度和高度与前文的模型相同，而斜坡角度则分别取为10°、20°和30°。保持粗糙元的安装位置和高度不变，相当于粗糙元长度变小，分别为4.54、2.20和1.39 mm。

3种不同斜坡角度的斜坡形粗糙元尾迹涡结构如图9所示，以无量纲Q=40 000的等值面表示，并以无量纲流向速度着色。不同角度的粗糙元尾迹涡结构相似，其涡管均失稳形成“发卡涡”结构，标志着流动开始转捩为湍流。在20° 斜坡的尾迹区，相干结构的尺度要明显小于10° 斜坡，并且尾迹的宽度更大，涡管开始变形的位置更靠近上游。对于30° 斜坡而言，其尾迹区涡结构与20° 斜坡几乎相同，涡管失稳的位置更靠前。

在斜坡形粗糙元1/2高度(y=0.4 mm)截面内的温度分布能更清晰地显示尾迹宽度及其失稳过程，如图10所示。粗糙元尾迹区内两侧出现稳定的低温条带结构，随着流动向下游发展，条带结构逐渐失稳形成规则扭曲，随后破碎成更小的流动结构，进入无序状态，流动转捩为湍流。对于10° 斜坡，条带结构扭曲的位置约为x=31.8 mm，20° 和30° 斜坡分别约为21.1 mm和16.4 mm。到达计算域出口(x=100 mm)位置，10° 斜坡的尾迹区宽度约为8.1 mm，而其他两个斜坡的尾迹宽度几乎相同，约为10.9 mm。

图9　不同斜坡角度的斜坡形粗糙元尾迹涡结构Fig.9　Wake vortex structures of ramp roughnesselements with different ramp angles

在斜坡形粗糙元对称面内，不同流向位置的湍动能最大值如图11所示，其可以表征尾迹扰动的发展过程。3个粗糙元的扰动发展过程类似，经过线性和非线性发展阶段之后，扰动进入饱和状态，标志着流动发生转捩。

图10　不同斜坡角度的斜坡形粗糙元y=0.4 mm截面温度分布Fig.10　Temperature distribution on y=0.4 mm cross-section of ramp roughness elements with different ramp angles

图11　不同斜坡角度的斜坡形粗糙元对称面的扰动沿流向发展Fig.11　Disturbance streamwise evolution on symmetry plane of ramp roughness elements with different ramp angles

在流向位置x=63.0 mm之前，10° 斜坡的扰动幅值最小，20° 斜坡居中，30° 斜坡扰动最大，可见随着斜坡角度增大，其逆压梯度增大，形成的扰动也随之增大。10° 斜坡的扰动线性增长区约为22.0 mm

在流向位置x=79.5 mm之后，3个斜坡造成的扰动幅值不再增长，几乎趋于统一水平，约为0.013。通过判断湍动能最大值的峰值位置，可以看出3个斜坡尾迹对称面处的转捩位置分别为x=79.0、54.0和52.5 mm。

3.2.2斜坡间距

斜坡形粗糙元的宽度和高度与3.1节的模型相同，斜坡角度为10°。选取两个粗糙元模型，粗糙元对称面之间的距离称为间距，记作Δ，取Δ=1.0d1、1.5d1和2.0d1这3种间距情况进行计算，如图12所示。展向设为周期边界条件。

图12　斜坡形粗糙元的间距示意图Fig.12　Schematic of interval space between ramproughness elements

图13　不同间距的斜坡形单元对称面的扰动发展Fig.13　Disturbance evolution on symmetry plane of ramp roughness elements with different interval space

图13给出了尾迹中的扰动发展过程。在粗糙元正后方平面内(z=0 mm)，分布式粗糙元的尾迹内扰动幅值更大，随着间距越小扰动幅值增加，但整体而言扰动幅值相差不大。对于Δ/d1=1.0的工况，其尾迹扰动在x=68.5 mm即到达峰值，转捩位置更靠前；而对于Δ/d1=1.5和2.0的工况，峰值位置与单个粗糙元情况几乎相同，约为75.5 mm。分布式粗糙单元尾迹扰动的线性增长率约为0.074，小于单个粗糙元的增长率0.099。

在z=0.8 mm平面内，分布式粗糙元尾迹扰动幅值大于单个粗糙元情况，Δ/d1=1.0工况的扰动幅值与其他3种情况差距明显，在扰动线性发展阶段其幅值约高出其他3种工况1～2个数量级，并且其扰动饱和位置更靠前，约为x=55.5 mm；Δ/d1=1.5和2.0工况的扰动幅值相近，转捩位置约为x=61.5 mm和66.0 mm；单个粗糙元的转捩位置最为靠后，约为x=77.0 mm。

z=1.6 mm截面内的扰动发展情况与z=0.8 mm 截面类似，Δ/d1=1.0工况扰动的幅值和饱和位置均领先于其他工况，转捩位置为x=68.0 mm，Δ/d1=1.5和 2.0工况的转捩位置为74.5 mm和82.5 mm，单个粗糙元的转捩位置约为x=91.5 mm。

4　结　论

1) 粗糙元尾迹区内的三维剪切层失稳是流动转捩的主要原因。对于不同形状的粗糙元，斜坡形的湍流尾迹最窄，圆柱形的湍流尾迹最宽；钻石形和圆柱形粗糙元下游的转捩位置更靠前，斜坡形的转捩位置稍微靠后。

2) 钻石形和圆柱形粗糙元引起的热流峰值远高于斜坡形粗糙元的热流峰值；钻石形粗糙元的热流峰值稍小于圆柱形。综合转捩效果与引起的热流峰值来看，斜坡形粗糙元可以作为较好的转捩触发装置。

3) 随着斜坡粗糙元角度的增大，其钝度随之增大，上游逆压梯度增强，尾迹区宽度增大，尾迹扩张角增大，但是20° 斜坡与30° 斜坡几乎没有差距；尾迹区扰动幅值增大，线性增长率减小，转捩位置提前，流动转捩位置相同

4) 随着粗糙元之间的间距减小，其造成的扰动幅值增大；扰动线性增长率几乎相同，但小于单个粗糙元工况；尾迹区转捩距离提前。综合比较，粗糙元的安装间距Δ/d1=1.0时，触发转捩效果最优。

致　谢

感谢清华大学信息科学与技术国家实验室提供计算资源。感谢中航工业产学研工程项目“航空CFD共用软件体系中的若干关键技术研究”的资助。

[1]WHITEHEAD A, JR. NASP aerodynamics: AIAA-1989-5013[R]. Reston: AIAA, 1989.

[2]VAN DRIEST E R, BLUMER C B. Boundary-layer at supersonic speeds-three dimensional roughness effects (spheres):SID 61-275[R]. Wichita: North American Aviation, Inc., 1961.

[3]赵慧勇， 周瑜， 倪鸿礼, 等. 高超声速进气道边界层强制转捩试验[J]. 实验流体力学，2012, 26(1): 1-6.

ZHAO H Y, ZHOU Y, NI H L, et al. Test of forced boundary-layer transition on hypersonic inlet [J]. Journal of Experiments in Fluid Mechanics, 2012, 26(1): 1-6 (in Chinese).

[4]SCHNEIDER S P. Effects of roughness on hypersonic boundary-layer transition[J]. Journal of Spacecraft and Rockets, 2008, 45(2)： 193-209.

[5]CASPER K M, WHEATON B M, JOHNSON H B, et al. Effect of freestream noise on roughness-induced transition at Mach 6: AIAA-2008-4291[R]. Reston: AIAA, 2008.

[6]VAN DRIEST E R, MCCAULEY W. The effect of controlled three-dimensional roughness on boundary layer transition at supersonic speeds[J]. Journal of Aerospace Science, 1960, 27(4): 261-271

[7]HICKS R M, HARPER W R, JR. A comparison of spherical and triangular boundary-layer tips on a flat plate at supersonic speeds: NASA, TM-X-2146[R]. Washington, D.C.: NASA, 1970.

[8]BERRY S A, AUSLENDER A H. Hypersonic boundary-layer trip development for hyper-X[J]. Journal of Spacecraft and Rockets, 2001, 38(6): 853-864.

[9]WHITEHEAD A H, JR. Flowfield and drag characteristics of several boundary-layer tripping elements in hypersonic flow: NASATND-5454[R]. Washington, D.C.: NASA, 1969.

[10]TIRTEY S C, CHAZOT O, WALPOT L. Characterization of hypersonic roughness-induced boundary-layer transition [J]. Experiments in Fluids, 2011, 50(2): 407-418.

[11]DANEHY P M, IVEY C B, INMAN J A, et al. High-speed PLIF imaging of hypersonic transition over discrete cylindrical roughness: AIAA-2010-0703[R]. Reston: AIAA, 2010.

[12]DANEHY P M, BATHEL B F, IVEY C B, et al. NO PLIF study of hypersonic transition over a discrete hemispherical roughness element: AIAA-2009-0394[R]. Reston: AIAA, 2009.

[13]周玲， 阎超， 孔维萱. 高超声速飞行器前体边界层强制转捩数值模拟[J]. 航空学报， 2014， 35(6): 1487-1495.

ZHOU L, YAN C, KONG W X. Numerical simulation of forced boundary layer transition on hypersonic vehicle forebody[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(6): 1487-1495 (in Chinese).

[14]BERNARDINI M, PIROZZOLI S, ORLANDI P. Compressibility effects on roughness-induced boundary layer transition[J]. International Journal of Heat and Fluids Flow, 2012, 35(35): 45-51.

[15]BARTKOWICZ M D, SUBBAREDDY P K, CANDLER G V. Numerical simulations of roughness induced instability in the purdue mach 6 wind tunnel: AIAA-2010-4723[R]. Reston: AIAA, 2010.

[16]IYER P S, MAHESH K. High-speed boundary layer transition induced by a discrete roughness element[J]. Journal of Fluid Mechanics, 2013, 729: 524-562.

[17]MUPPIDI S, MAHESH K. Direct numerical simulations of roughness-induced transition in supersonic boundary layers[J]. Journal of Fluid Mechanics, 2012, 693: 28-56.

[18]TULLIO N D, PAREDES P, SANDHAM N D, et al. Laminar-turbulent transition induced by a discrete roughness element in a supersonic boundary layer[J]. Journal of Fluid Mechanics, 2013, 735: 613-646.

[19]SUN Z S, REN Y X, LARRICQ C, et al. A class of finite difference schemes with low dispersion and controllable dissipation for DNS of compressible turbulence[J]. Journal of Computational Physics, 2011， 230(12)： 4616-4635.

[20]WANG Q J, REN Y X, SUN Z S. High resolution finite volume scheme based on minimized dispersion and controllable dissipation reconstruction[J]. Science China Physics, Mechanics & Astronomy, 2013, 56(2): 423-431.

[21]DUAN Z W, XIAO Z X, FU S. Direct numerical simulation of hypersonic transition induced by an isolated cylindrical roughness element[J]. Science China Physics, Mechanics & Astronomy, 2014, 57(12): 2330-2345.

[22]DUAN Z W, XIAO Z X, FU S. Direct numerical simulation of hypersonic transition induced by a cylindrical roughness element: AIAA-2013-3112[R]. Reston: AIAA, 2013.

[23]WHEATON B M, SCHNEIDER S P. Roughness-induced instability in a hypersonic laminar boundary layer[J].AIAA Journal, 2012, 50(6): 1245-1256.

[24]WHEATON B M, BARTKOWICZ M D, SUBBAREDDY P K, et al. Roughness-induced instabilities at Mach 6: A combined numerical and experimental study: AIAA-2011-3248[R]. Reston: AIAA, 2011.

段志伟男， 博士， 助理研究员。主要研究方向： 空气动力学、 高精度湍流预测和边界层转捩。

Tel.: 010-62795411

E-mail: dzw15@tsinghua.edu.cn

肖志祥男，博士， 副研究员， 博士生导师。主要研究方向： RANS-LES混合方法、 高精度湍流预测、 流动转捩和计算气动声学。

Tel.: 010-62797060

E-mail: xiaotigerzhx@tsinghua.edu.cn

Roughness element induced hypersonic boundary layer transition

DUAN Zhiwei, XIAO Zhixiang*

School of Aerospace Engineering, Tsinghua University, Beijing100084, China

Hypersonic boundary layer transition from laminar to turbulent induced by different isolated roughness elements is investigated using direct numerical simulation based on finite volume formulation. To explore the transition mechanism through resolving the small flow structure, and capture shock wave in hypersonic flow, the high order minimized dispersion and controllable dissipation (MDCD) scheme is used to reconstruct the convection terms of Navier-Stokes equations. The numerical results agree well with experimental data. The numerical method adopted in this article is able to resolve small flow structures and their break-up and instability procedure. And it shows that the transition is dominated by the instability of the three-dimensional shear layer on top of the roughness elements. The effect of roughness element shape and geometrical parameters on transition mechanisms, and the transition results of multiple roughness elements are quantitatively studied.

hypersonic； roughness element； boundary layer transition； parameter effects; direct numerical simulation

2016-01-18； Revised： 2016-02-17； Accepted： 2016-04-26； Published online： 2016-04-2915：37

s： National Natural Science Foundation of China (11372159); China Postdoctoral Science Foundation (2015M571029)； National Key Research and Development Project (2016YFA0401200)

. Tel.： 010-62797060E-mail: xiaotigerzhx@tsinghua.edu.cn

2016-01-18； 退修日期： 2016-02-17； 录用日期： 2016-04-26;

时间： 2016-04-2915:37

www.cnki.net/kcms/detail/11.1929.V.20160429.1537.008.html

国家自然科学基金 (11372159)； 中国博士后科学基金 (2015M571029); 国家重点研发计划项目 (2016YFA0401200)

.Tel.： 010-62797060E-mail: xiaotigerzhx@tsinghua.edu.cn

10.7527/S1000-6893.2016.0130

V211.3

A

1000-6893(2016)08-2454-10

引用格式： 段志伟， 肖志祥. 粗糙元诱导的高超声速边界层转捩[J]． 航空学报, 2016, 37(8): 2454-2463. DUAN Z W, XIAO Z X. Roughness element induced hypersonic boundary layer transition[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2454-2463.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160429.1537.008.html