三角翼大迎角风洞试验支架干扰数值模拟研究
张军, 艾宇, 黄达, 刘晶
1.南京航空航天大学 航空宇航学院, 南京 210016 2.江南机电设计研究所 第二研究室, 贵阳 550009 3.吉宝-新加坡国立大学联合实验室, 新加坡市 117576
三角翼大迎角风洞试验支架干扰数值模拟研究
张军1,*, 艾宇2, 黄达1, 刘晶3
1.南京航空航天大学 航空宇航学院, 南京210016 2.江南机电设计研究所 第二研究室, 贵阳550009 3.吉宝-新加坡国立大学联合实验室, 新加坡市117576
现代战争要求战斗机能够在大迎角(AOA)状态下进行过失速飞行,对飞机大迎角绕流流场的研究主要的方法有风洞试验和数值模拟。在大迎角风洞试验中,常用的是尾支撑方法,支架的存在会对模型的试验结果产生一定的影响,本文通过数值模拟来对这个影响进行研究。以开源计算流体力学软件OpenFOAM 2.3为平台,采用PIMPLE算法求解Navier-Stokes(N-S)方程, PIMPLE算法是SIMPLE(Semi-Implicit Method for Pressure-linked Equations)算法和PISO(Pressure Implicit with Splitting of Operator)算法的结合体;采用基于有限体积的空间离散方法和空间二阶精度的线性插值方法,时间离散采用后向差分方法,湍流模型采用SA-DDES(Spalart-Allmaras-Delayed Detached Eddy Simulation)模型。为了验证方法的可靠性,首先对0°、10°、30°、50°、70° 以及90° 迎角下的有支架三角翼绕流流场进行计算,并将计算结果与试验结果进行对比,两者吻合较好。在此基础上,数值模拟了无支架的三角翼绕流流场,对比有/无支架情况下数值模拟结果,得到支架对三角翼绕流流场、背风面压强分布和气动力的影响。计算结果表明:大迎角情况下,有支架与无支架时相比,支架的存在会影响三角翼附近的流场(但是不会改变涡系等流动结构)、改变翼表面压强分布,从而导致三角翼的法向力系数和俯仰力矩系数发生明显变化。
大迎角; 三角翼; 非定常流场; OpenFOAM; SA-DDES; 大涡模拟
对三角翼大迎角(Angle of Attack,AOA)绕流流场研究的主要方法有风洞试验和数值模拟。风洞试验可以提供较为精确的气动力数据[1-10],在大迎角风洞试验中,常用的是尾支撑方法,由于支撑装置的存在,使绕模型的流场发生改变,从而对模型的试验结果(包含空间流场、表面压强分布和气动力等)产生一定的干扰,据作者了解,目前国内外通常都没有对采用尾撑方式的低速大迎角风洞试验中的支架干扰进行相应的扣除。
对于尾支杆干扰的风洞试验修正,文献[1]已经进行了较为深入的研究, YF-16及DBM-01标模尾支杆的影响分析结果表明:在小迎角附近,尾支杆的影响较小;在大迎角(大于20°)时,升力和阻力干扰迅速增加,尾支杆干扰非常明显,当模型YF-16的迎角为36.5° 时,尾支杆对俯仰力矩系数的干扰量达到20%,由此可见,对尾支杆干扰进行研究是很有必要的。
一些学者[2-5]对尾支杆的影响进行了卓有成效的研究。文献[2] 采用试验方法研究了不同的尾支杆对低速大迎角风洞试验结果的影响,研究结果表明:在中小迎角范围内,不同形式尾支杆的支架干扰量随迎角变化不大;在大迎角状态下,不同形式尾支杆的支架干扰量差异较大,需要开展相应的支架干扰研究,以获得较为准确的低速大迎角试验结果。文献[3]的试验结果也表明,大迎角区域内尾支杆对飞机纵向的近场干扰量较大。文献[4-5]采用数值模拟方法研究了尾支杆的影响,其中文献[4]采用k-ω剪切应力传输(SST)湍流模型数值研究了小展弦比飞翼标模在0.6、0.9和1.5这3个典型马赫数下的尾支杆干扰特性,计算迎角最大为18°,侧重于研究不同尾支杆对涡破裂位置以及模型气动力的影响。
三角翼大迎角非定常流场中具有不同时间、空间尺度的涡结构,十分复杂,常采用雷诺平均Navier-Stockes (Reynolds Average Navier-Stockes, RANS) 和大涡模拟(Large Eddy Simulation, LES)方法对这一复杂流场进行数值模拟。
王光学等[11]采用SST湍流模型及具有5阶空间精度的WCNS-E-5插值格式对具有65° 后掠角的三角翼进行了数值模拟,主要研究WCNS-E-5插值格式对三角翼涡破裂计算的适用性以及激波对涡破裂点位置的影响。同年,他们又通过WCNS-E-5对三角翼涡破裂进行了数值模拟,重点研究了三角翼大迎角漩涡破裂点的突然前移[12]。另外许多学者也对三角翼的气动力特性做了研究[13-20]。其中杨小亮等[13]对80° 后掠三角翼强迫俯仰、自由滚转双自由度耦合运动特性做了数值研究。韩冰等[18]采用Spalart-Allmaras(SA)湍流模型,通过耦合求解Navier-Stokes 方程与滚转运动方程,比较研究了不同后掠角的双三角翼和翼身组合体的滚转运动特性,得到了有意义的结果。
Spalart等[21]在1997年将RANS和LES各自的优点结合起来提出了分离涡模拟(Detached-Eddy-Simulation, DES)的思想,DES的思想是将RANS和LES结合,使其具有两者的优点,从而更加适用于非定常流场计算。Li等[22]利用DES方法,对双三角翼在40° 和70° 迎角情况下的涡流动进行了数值分析,分析结果显示,错流涡旋对压力的分布有影响,它可导致10%~20%的偏差。
DES对于流场的计算具有较好的精度,但是它也有自己的不足,主要表现为当网格尺寸减小到一定的程度时,导致流场边界层使用DES中的LES部分进行计算,但是如果边界层内的网格尺寸不足以分辨湍流脉动时,这就将导致涡黏系数降低,计算结果偏差较大。
为了消除模型应力损耗的影响,Spalart提出了延迟脱体涡方法(Delayed Detached Eddy Simulation, DDES)思想[23],DDES模型将计算区域划分与流场的变化相结合,并不是单纯地依靠当地网格尺寸,这样可以有效地避免模型应力损耗的影响。Lüdeke和Leicher[24]利用DDES模型对战斗机大迎角飞行进行了非定常流场数值模拟。
本文用数值模拟方法研究支架干扰对试验结果的影响,以开源软件OpenFOAM2.3为平台,采用SA-DDES湍流模型,对有/无支架后掠60° 三角翼在不同迎角下的流场进行计算,对比分析了支架对翼背风区流场、背风面压强分布和气动力参数的影响。
1 模型建立及网格划分
为了使数值模拟模型尽量和试验状态符合,在建模的时候,考虑了整个支架和风洞试验段的尺寸,以方便计算和试验结果的比较。
以60° 后掠三角翼为对象,如图1所示,其前缘后掠角为60°,后缘展长为0.69 m,平均气动弦长L为0.393 8 m,模型前后缘上下翼面夹角为25°。试验中,在三角翼模型的根弦处有一中空圆柱用于和支架连接,如图2所示。为了生成高质量的网格,将整个流域分为内、外两个区域,分别为区域A和区域B。A、B两区域由直径D=2.3 m的球面分开,球心与三角翼几何中心重合,有/无支架的三角翼以及球面组成了区域A,如图3 所示。图4表示的是区域B的范围,区域B的外边界截面形状为2.5 m×3 m的切角矩形,整个流域长为7 m。
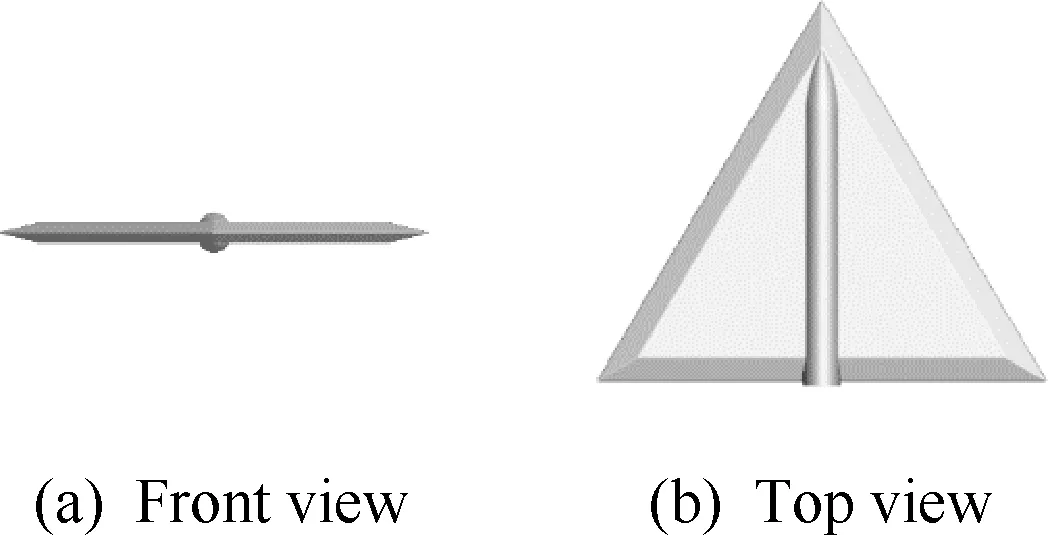
图1 三角翼外形图Fig.1 Delta wing geometry
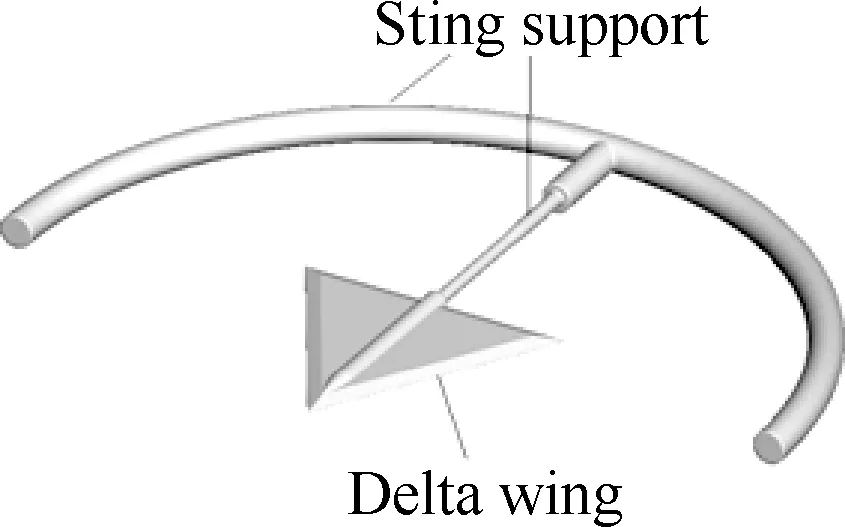
图2 三角翼和支架外形图Fig.2 Delta wing and sting support geometries

图3 计算域AFig.3 Computational domain A
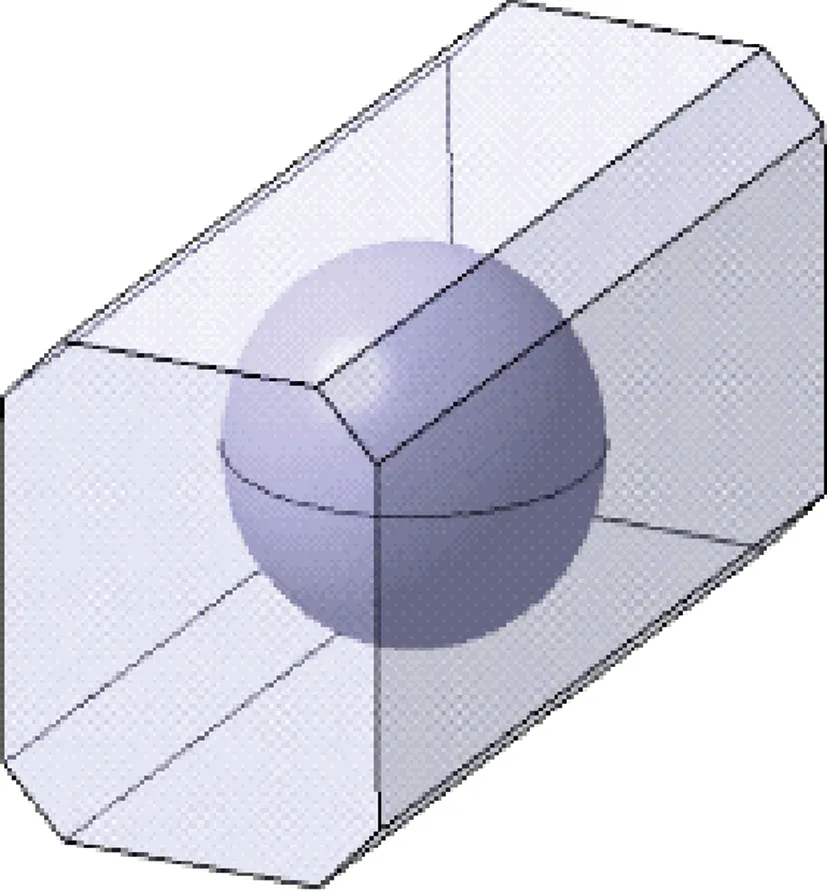
图4 计算域BFig.4 Computational domain B
采用非结构四面体网格对整个流域进行网格划分,在三角翼附近生成三棱柱边界层网格,边界层的第一层网格高度为0.01 mm。三角翼表面网格尺寸约为1.5 mm,共有三角形单元约23.9万个;整个计算域共生成四面体单元约2 358万个(有支架)/2 140万个(无支架),翼表面边界层棱柱网格约288万。
2 数值模拟方法及验证
控制方程为Navier-Stokes方程,采用PIMPLE算法求解Navier-Stokes方程, PIMPLE算法是SIMPLE(Semi-Implicit Method for Pressure-linked Equations)算法和PISO(Pressure Implicit with Splitting of Operator)算法的结合体。采用基于有限体积的空间离散方法和空间二阶精度的线性插值方法,时间离散采用二阶精度的后向差分方法,湍流模型采用SA-DDES模型。
计算域的入口设为速度入口、出口设为压强出口边界条件,翼面以及支架设为固壁,采用无滑移边界条件,计算域外壁采用对称边界条件,来流风速为30 m/s。
对迎角为0°、10°、30°、50°、70° 以及90° 的有支架三角翼绕流流场进行模拟。三角翼的平均气动弦长L=0.398 3 m,为了对流场进行分析,定义距离翼头部0.56L、0.83L、1.13L和1.42L这4个截面。图5给出30°、50° 和70° 迎角下,0.56L、0.83L、1.13L和1.42L截面上的流线图。表1、表2和图6(其中,NUAA表示南京航空航天大学试验结果,HIT表示哈尔滨工业大学试验结果)分别给出法向力系数CN(参考面积为三角翼俯视面积S=0.206 16 m2)和俯仰力矩系数Cm(参考长度为平均气动弦长L,力矩参考点为翼几何中心)的计算和试验结果对比。
流体流过具有一定迎角的三角翼时,在翼的背风区域形成旋转方向相反的前缘脱体分离涡,并向尾部发展,涡核逐渐增大。主涡分离线与流体的来流方向是斜交叉的,涡分离轴线与前缘保持相似分布。分离涡的涡矢量可以分解为轴向分量和法向分量,轴向分量与涡轴线平行,保证了涡的形成,法向分量与涡轴线垂直,保证了涡沿轴线发展。
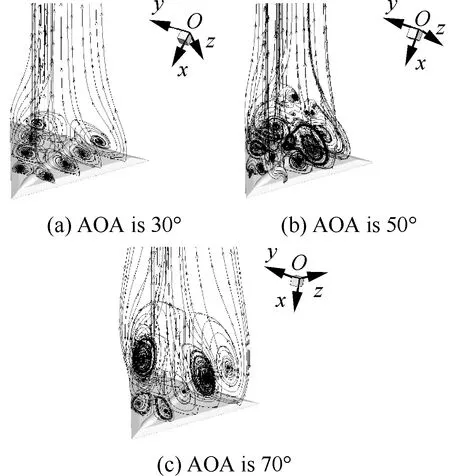
图5 不同迎角(AOA)下0.56L、0.83L、1.13L和 1.42L 截面上的流线图Fig.5 Streamlines on planes of 0.56L, 0.83L, 1.13L and 1.42L at different angles of attack (AOAs)
表1 法向力系数(CN)计算和试验结果对比
Table 1Comparison of normal force coefficients (CN) between numerical and test results
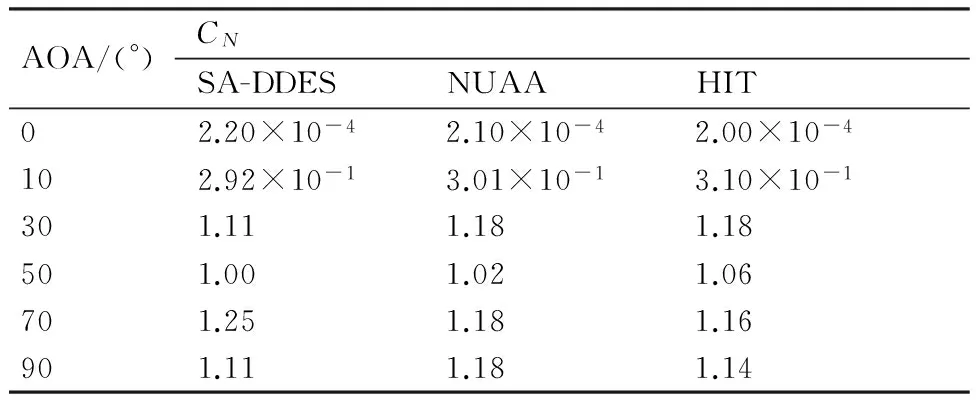
AOA/(°)CNSA-DDESNUAAHIT02.20×10-42.10×10-42.00×10-4102.92×10-13.01×10-13.10×10-1301.111.181.18501.001.021.06701.251.181.16901.111.181.14
表2俯仰力矩系数(Cm)计算和试验结果对比
Table 2Comparison of pitching moment coefficients (Cm) between numerical and test results
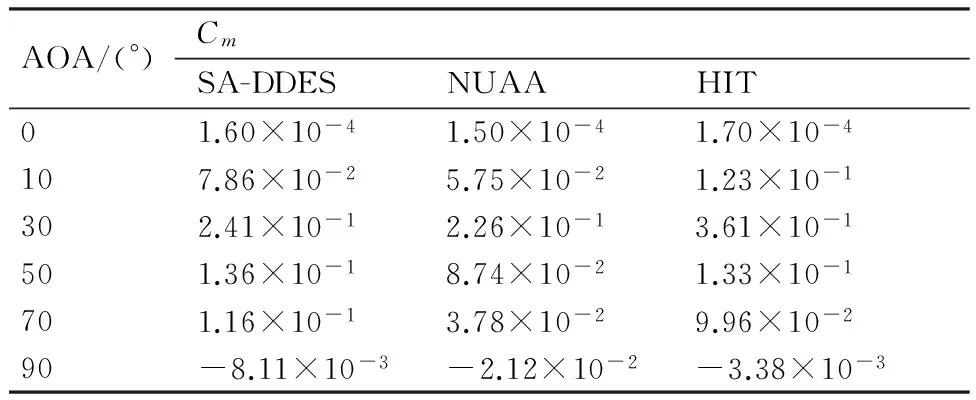
AOA/(°)CmSA-DDESNUAAHIT01.60×10-41.50×10-41.70×10-4107.86×10-25.75×10-21.23×10-1302.41×10-12.26×10-13.61×10-1501.36×10-18.74×10-21.33×10-1701.16×10-13.78×10-29.96×10-290-8.11×10-3-2.12×10-2-3.38×10-3
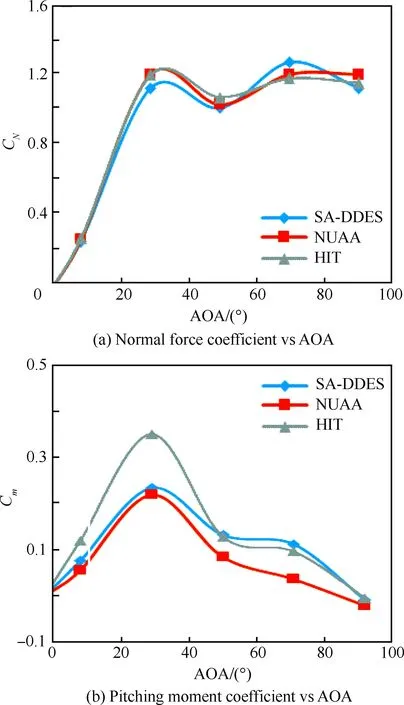
图6 不同迎角下计算和试验结果的对比Fig.6 Comparison between numerical and test results at different AOAs
当迎角较小时,由于未发生涡破裂现象,在三角翼背风区域两侧旋转分离涡系相互独立,互不干扰,如图5(a)所示,同时,涡核与翼面之间的距离,沿着流动方向,越来越大。当迎角为30° 时,由于背风区的涡未发生破裂,前缘涡的强度最强(见图5(a)),翼背风面负压达到极大值,此时CN和Cm均达到极大值。由于涡升力主要是前缘涡提供,所以前缘涡破裂之前,CN随迎角变大是单调上升的,当前缘涡破裂后,CN突然下降。当迎角为50° 时(见图5(b)),处于涡完全破裂状态,这时流动变得不稳定,背风区两侧对称涡系互相干扰,翼背风面负压有所减小,导致CN和Cm均减小。当迎角为70° 时,翼背风区出现了大尺度涡脱落现象(见图5(c)),迎角增大,涡量增强,涡系之间的干扰更加强烈,翼背风面负压有所增加,导致CN也相应增加。
从表1、表2以及和图6可以看出,由于试验误差,NUAA和HIT的CN有些差别,但相差不大;Cm的差别要大一些,尤其是在迎角为30° 时相差最大,NUAA是0.226,HIT是0.361,SA-DDES计算结果是0.241,由于本文采用NUAA的试验模型进行计算,所以和NUAA的试验结果比较接近。从表1、表2和图6可以看出SA-DDES模型计算得到的结果还是比较合理的。
3 支架影响的数值模拟
在对数值方法验证的基础上,对无支架情况的流场进行数值模拟,有/无支架三角翼背风区流线对比如图7所示,三角翼背风面压力系数分布对比如图8所示,法向力系数CN和俯仰力矩系数Cm的对比如表3和表4所示。
图7给出了不同迎角下三角翼背风区的流线图,图7(a)中,迎角为10°,由于迎角较小,在三角翼背风区没有形成三维旋转分离涡。但是,随着迎角进一步增大,在翼背风区产生剪切层分离,形成旋转方向相反的前缘脱体分离涡,并向尾部发展,涡核逐渐增大,如图7(b)所示。从图7(a)和图7(b)可以看出,迎角小于等于30° 时,支架对流场无明显影响,流线基本相似。当迎角从30° 增大到50° 时,发生了涡破裂现象,随着迎角的增大,涡破裂点向翼头部移动,在迎角为50° 时,处于涡完全破裂状态,导致法向力系数CN减小,如图7(c)。当迎角增加到70° 和90° 后,翼背风区出现了大尺度涡脱落现象,如图7(d)和图7(e)所示。在迎角为50°、70° 和90° 时,支架对流场有一定的影响,其中70° 迎角时的影响较大。从有/无支架的翼背风区流线对比可以看出,支架的存在对翼背风区流场有一定的影响,迎角较小时,影响较小,迎角较大时,影响较大,支架对背风区流场的影响随着迎角的增大而增大。虽然支架的影响明显,但是并没有改变背风区涡破裂点的位置,有/无支架情况下涡系结构相似。
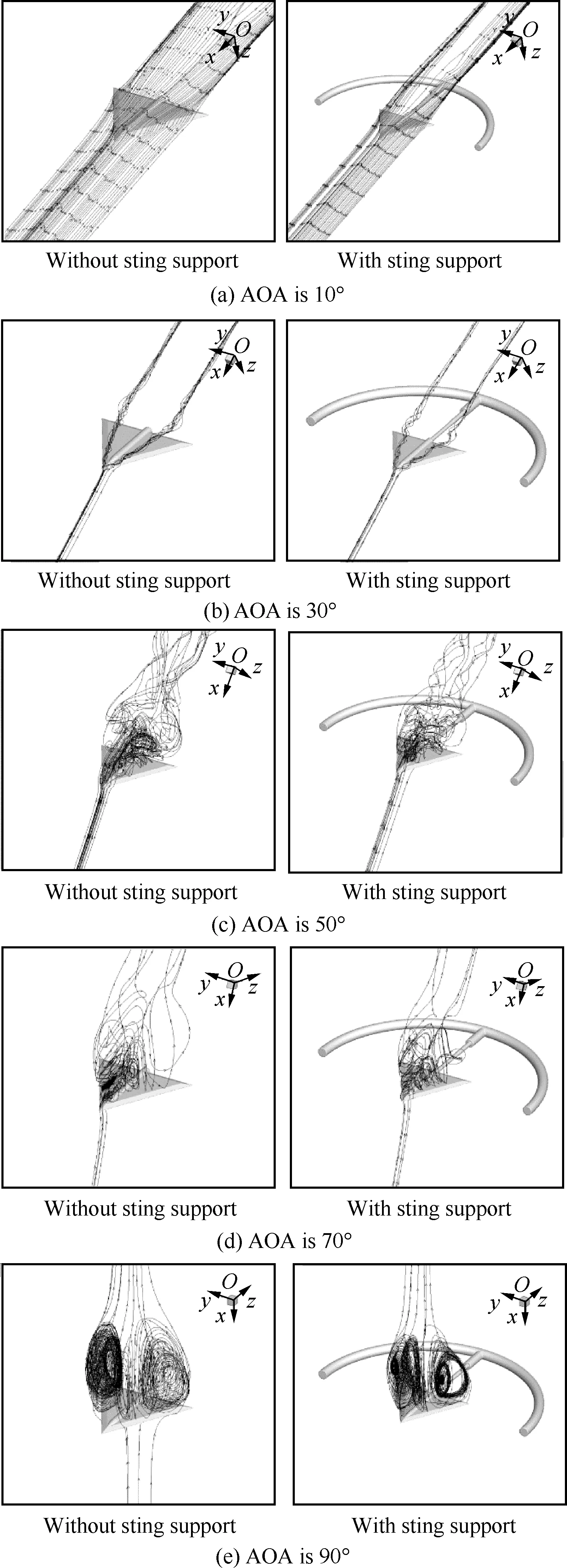
图7 不同迎角下有/无支架三角翼背风区流线图对比Fig.7 Comparison of streamlines of delta wing leeward side with and without sting support at different AOAs
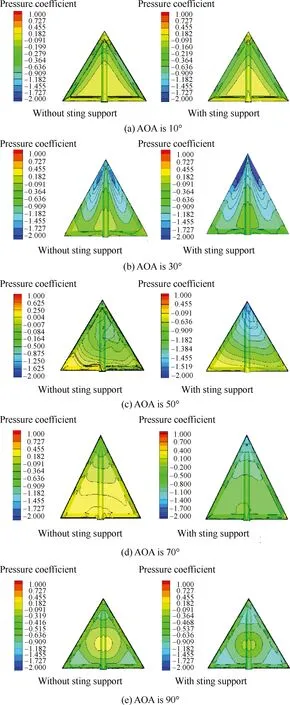
图8 不同迎角下有/无支架三角翼背风区压力系数对比Fig.8 Comparision of pressure coefficients of delta wingleeward side with and without sting support at >different AOAs
机翼背风区流场的差异,将会导致机翼背风面压强系数的分布有一定的差异,图8给出了不同迎角下机翼背风面压强系数的分布云图。由于分离涡的出现,使得位于涡核下方的机翼表面产生了较低的压强,如图8所示。在10° 迎角时,低压区域主要集中在三角翼背风面两侧,如图8(a)所示,此时支架对背风面压强系数的影响不明显。迎角为30° 时,三角翼背风面的局部区域在前缘分离涡的作用下产生了流速相对其他区域较高的流动,这就使位于涡核下方的三角翼前缘的压强很低,如图8(b)所示。迎角为30°、50°和70°(对应图8(b)、图8(c)和图8(d))时,支架导致翼背风面负压增大,尤其是在靠近翼头部位置,负压明显增大。当迎角为90° 时,由于此时三角翼相当于是将一块三角形平板垂直放置于流场中,因此三角翼的背风区3个角的流动情况基本是相似的,其背风面压强系数的分布也基本一致,只是平均负压增大,如图8(e)所示。在30°、50°、70° 和90° 迎角时,支架对三角翼背风面压强系数分布有明显的影响,使其负压变大;在迎角为30°、50° 和70° 时,翼背风面靠近头部位置的负压明显增大。
从图8中可以看出支架对三角翼背风面的压强系数分布产生影响,这种影响可能导致CN和Cm发生变化,见表3和表4。从表3和表4的CN和Cm数据可以看出,由于支架影响,三角翼在有/无支架情况下的CN和Cm有明显差异。这是由于支架阻塞了风洞,导致当地风速增大;支架本身也对三角翼附近流场产生干扰,促使了机翼表面压强分布的变化,从而导致三角翼的CN和Cm发生了一定的变化。支架的存在使三角翼CN偏大,迎角大于等于30° 时,Cm也偏大,迎角越大,Cm偏差越大。
表3有/无支架时法向力系数(CN)的对比
Table 3Comparison of normal force coefficients (CN) with and without sting support
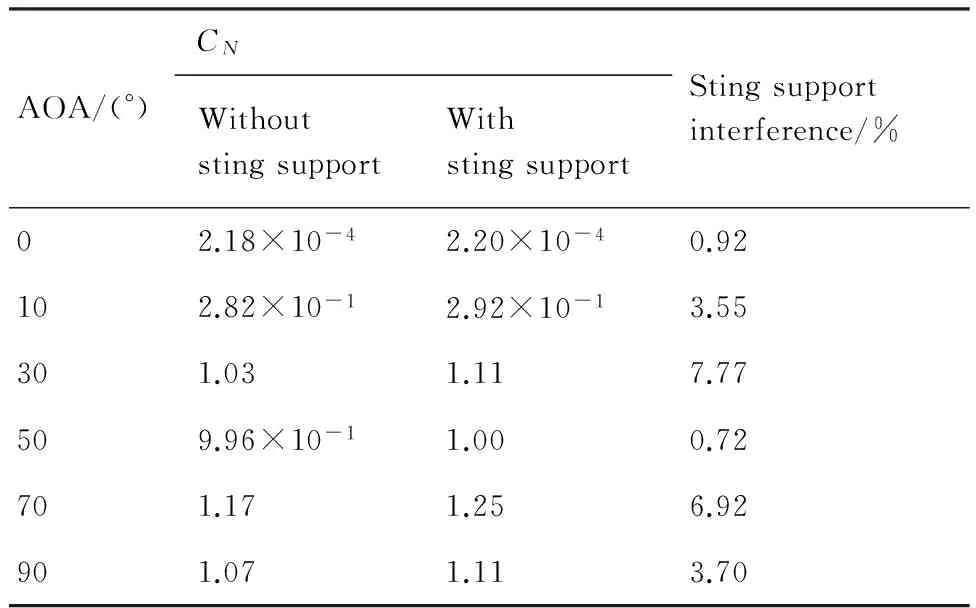
AOA/(°)CNWithoutstingsupportWithstingsupportStingsupportinterference/%02.18×10-42.20×10-40.92102.82×10-12.92×10-13.55301.031.117.77509.96×10-11.000.72701.171.256.92901.071.113.70
表4有/无支架时俯仰力矩系数(Cm)的对比
Table 4Comparison of pitching moment coefficients (Cm) with and without sting support
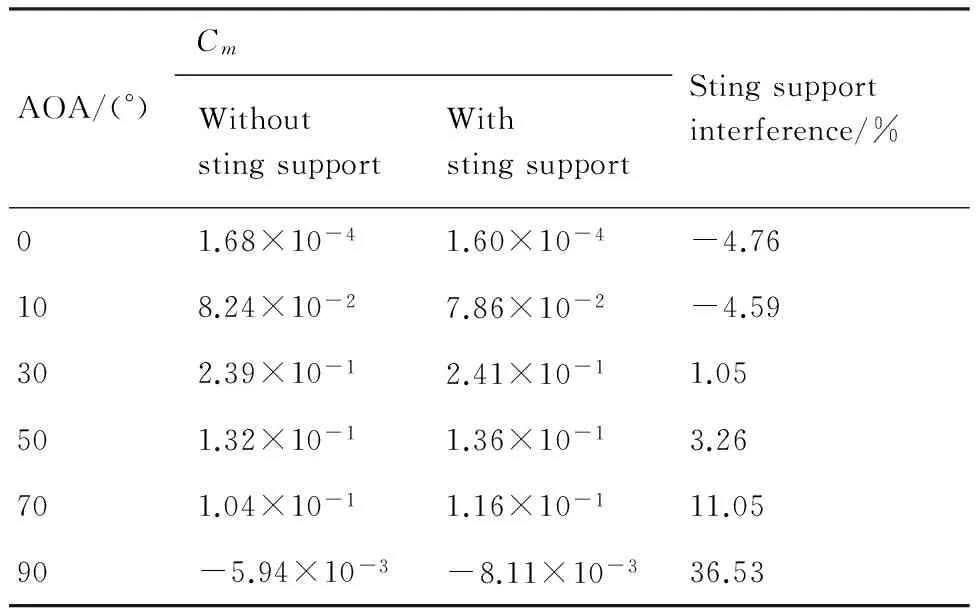
AOA/(°)CmWithoutstingsupportWithstingsupportStingsupportinterference/%01.68×10-41.60×10-4-4.76108.24×10-27.86×10-2-4.59302.39×10-12.41×10-11.05501.32×10-11.36×10-13.26701.04×10-11.16×10-111.0590-5.94×10-3-8.11×10-336.53
表3和表4中,Sting support interference是支架干扰量相对于无支架情况的百分比,迎角为0° 时,CN和Cm均不等于0,这是由数值计算误差产生的。迎角为30° 时,支架对CN的干扰量达到最大为7.77%;迎角为50° 时,支架对CN的干扰量为0.72%,基本没有影响,其原因还需要进一步的研究。
支架对Cm的干扰量随着迎角的变大而逐渐向正的方向变大:迎角为10° 时,支架干扰量为-4.76%;迎角为70° 时,达到最大为11.05%。迎角为90° 时,支架干扰量达到36.53%,这是由Cm值本身较小导致的。
4 结 论
以OpenFOAM 2.3为平台,采用SA-DDES模型对有/无支架三角翼模型在不同迎角下的流场进行数值模拟,通过对比分析不同迎角下三角翼背风区流线、背风面压强系数分布以及法向力系数CN和俯仰力矩系数Cm的变化,研究支架对流场以及三角翼气动力的影响,其结果表明:
1) 支架的存在对翼背风区流线有一定的影响,但是影响不大,不足以改变背风区涡破裂点的位置等涡系结构;支架对背风区流线的影响随着迎角的增大而增大。
2) 支架对三角翼背风面压强系数分布有明显的影响,使其负压变大;当迎角大于等于30° 时,翼背风面头部负压明显增大。
3) 由于支架对三角翼背风面压强系数分布有明显的影响,CN和Cm等气动力参数也随之发生变化。支架的存在使三角翼CN偏大,迎角为30° 时,支架干扰量达到最大为7.77%;支架对Cm的干扰量随着迎角的变大而逐渐向正的方向偏大,迎角为70° 时,支架干扰量达到最大为11.05%。
4) 对不同迎角下的支架干扰量进行了定性分析和定量研究,本文的数值计算结果可以为类似低速风洞试验模型的支架干扰修正提供参考。
[1]程厚梅. 风洞实验干扰与修正[M]. 北京: 国防工业出版社, 2003: 197.
CHEN H M.Interference and correction in wind tunnel experiment[M]. Beijing: National Defense Industry Press, 2003: 197 (in Chinese).
[2]王勋年, 祝明红, 孙传宝. 低速大迎角尾撑支架干扰试验研究[J]. 实验流体力学, 2007, 21(2): 8-12.
WANG X N, ZHU M H, SUN C B.Investigation on the interference of rear sting supports at high angle of attack in low speed wind-tunnel[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(2): 8-12 (in Chinese).
[3]祝明红, 孙海生, 金玲, 等. 低速大迎角张线尾撑系统支架干扰影响研究[J]. 实验流体力学, 2011, 25(3): 1-5.
ZHU M H, SUN H S, JIN L, et al. Study on the support interference of wire-assistant sting support at high angle of attack in low speed wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(3): 1-5 (in Chinese).
[4]苏继川, 黄勇, 李永红, 等. 小展弦比飞翼亚、跨、超声速支撑干扰研究[J]. 空气动力学学报, 2015, 33(3): 289-295.
SU J C, HUANG Y, LI Y H, et al. Support interference of low-aspect-ratio flying-wing from subsonic to supersonic speed[J]. Acta Aerodynamica Sinica, 2015, 33(3): 289-295 (in Chinese).
[5]杨贤文, 刘昕. 运输机模型高速风洞试验支撑形式及支撑干扰研究[J]. 空气动力学学报, 2015, 33(6): 721-727.
YANG X W, LIU X. Support form and support interference on transport aircraft model in high speed wind tunnel[J]. Acta Aerodynamica Sinica, 2015, 33(6): 721-727 (in Chinese).
[6]唐敏中, 李周复, 于文勇, 等. 三角翼低速动态大攻角气动特性试验研究[J]. 空气动力学学报, 1994, 12(4): 367-374.
TANG M Z, LI Z F, YU W Y, et al. Experimental study on aerodynamic characteristics of delta wing at low speed and high angle of attack[J]. Acta Aerodynamica Sinica, 1994, 12(4): 367-374 (in Chinese).
[7]张文华, 李志强, 丁克文, 等. 三角翼过失速非定常洞壁干扰修正[J]. 航空学报, 1997, 18(2): 215-219.
ZHANG W H, LI Z Q, DING K W, et al. Unsteady wall corrections for a delta wing oscillating in pitch to very high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 1997, 18(2): 215-219 (in Chinese).
[8]黄达, 李志强, 丁克文, 等. 三角翼大幅度俯仰运动非定常洞壁干扰实验研究[J]. 南京航空航天大学学报, 2003, 35(1): 13-17.
HUANG D, LI Z Q, DING K W, et al. Wall interference in unsteady force tests for delta wing in large amplitude pitching motions[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2003, 35(1): 13-17 (in Chinese).
[9]SUN H S, JIANG Y B, LIU Z T, et al. Experimental research on the high angle of attack aerodynamic characteristics of an 80°/65° double-delta wing[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(6): 6-12.
[10]陶洋, 赵忠良, 李浩, 等. 80°/65°双三角翼滚转稳定特性预测研究[J]. 实验流体力学, 2013(6): 43-46.
TAO Y, ZHAO Z L, LI H, et al. Investigation on dynamic behavior forecast of 80°/65° double-delta wing in roll at high incidence[J]. Journal of Experiments in Fluid Mechanics, 2013(6): 43-46 (in Chinese).
[11]王光学, 邓小刚, 刘化勇, 等. 高阶精度格式WCNS在三角翼大攻角模拟中的应用研究[J]. 空气动力学学报, 2012, 30(1): 28-34.
WANG G X, DENG X G, LIU H Y, et al. Application of high-order scheme (WCNS) at high angles of incidence for delta wing[J]. Acta Aerodynamica Sinica, 2012, 30(1): 28-34 (in Chinese).
[12]王光学, 邓小刚, 王运涛, 等. 三角翼涡破裂的高精度数值模拟[J]. 计算物理, 2012, 29(4): 489-494.
WANG G X, DENG X G, WANG Y T, et al. High-order numerical simulation of vortex breakdown on delta wing[J]. Chinese Journal of Computational Physics, 2012, 29(4): 489-494 (in Chinese).
[13]杨小亮, 刘伟, 赵云飞, 等. 80° 后掠三角翼强迫俯仰、自由滚转双自由度耦合运动特性数值研究[J]. 空气动力学学报, 2011, 29(4): 421-426.
YANG X L, LIU W, ZHAO Y F, et al. Numerical investigation of the characteristics of double degree-of-freedom motion of an 80° delta wing in force-pitch and free-roll[J]. Acta Aerodynamica Sinica, 2011, 29(4): 421-426 (in Chinese).
[14]黄国创, 王玉明, 曹桂兴. 三角翼大攻角俯仰振荡的动力学“滞后”现象机理研究[J]. 中国科学(A辑), 1994, 24(5): 498-504.
HANG G C, WANG Y M, CAO G X. Study on the mechanism of the dynamic “lag” in the large angle of attack of the delta wing[J]. Science in China (Series A), 1994, 24(5): 498-504 (in Chinese).
[15]李沛峰, 张彬乾. 三角翼大迎角绕流特性数值模拟的网格处理技术研究[J]. 航空计算技术, 2008, 38(2): 22-26.
LI P F, ZHANG B Q. Study on grid generation of numerical simulation for vortical flow over a delta wing at high angle of attack[J]. Aeronautical Computing Technique, 2008, 38(2): 22-26 (in Chinese).
[16]刘昕, 陈亮中, 林敬周. 双三角翼拉升流场特性数值模拟研究[J]. 计算力学学报, 2012, 29(6): 905-911.
LIU X, CHEN L Z, LIN J Z. Numerical simulation on dynamic characteristics of double-delta wing flow field during pitch-up motion[J]. Chinese Journal of Computational Mechanics, 2012, 29(6): 905-911 (in Chinese).
[17]刘杰, 刘沛清, 闫指江. 中等后掠角三角翼前缘双涡结构的形成机理数值研究[J]. 空气动力学学报, 2012, 30(6): 767-771.
LIU J, LIU P Q, YAN Z J. Numerical investigations of formation mechanism about a dual leading-edge vortex structure of a delta wing with medium leading-edge sweep angle[J]. Acta Aerodynamica Sinica, 2012, 30(6): 767-771 (in Chinese).
[18]韩冰, 徐敏, 李广宁, 等. 双三角翼及其翼身组合的滚转运动特性比较研究[J]. 航空学报, 2014, 35(2): 417-426.
HAN B, XU M, LI G G, et al. Comparative research on the dynamic rolling characteristics of double delta wing and wing-body configuration[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 417-426 (in Chinese).
[19]张付昆, 李栋. 前缘钝度和雷诺数对三角翼流场的影响[J]. 科学技术与工程, 2013, 13(16): 4741-4746.
ZHANG F K, LI D. Reynolds numbers and leading-edge bluntness effects on delta wing[J]. Science Technology and Engineering, 2013, 13(16): 4741-4746 (in Chinese).
[20]李喜乐, 杨永. 带副翼偏转的三角翼自由滚转运动数值模拟[J]. 航空学报, 2012, 33(3): 453-462.
LI X L, YANG Y. Numerical simulation of the free rolling motion of a delta wing configuration with aileron deflection[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(3): 453-462 (in Chinese).
[21]SPALART P R, JOU W H, STRELETS M, et al. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach[J]. Advances in DNS/LES, 1997(1): 4-8.
[22]LI Q, SUN D, ZHANG H X. Detached-eddy simulations and analysis on new vertical flows over a 76/40° double delta wing[J]. Science China Physics, Mechanics & Astronomy, 2013, 56(6): 1062-1073.
[23]SPALART P R,DECK S, SHUR M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theoretical and Computational Fluid Dynamics, 2006, 20(2): 181-195.
[24]LÜDEKE H, LEICHER S. Unsteady CFD analysis of a delta wing fighter configuration by delayed detached eddy simulation[M]//Advances in Hybrid RANS-LES Modeling. Berlin Heidelberg: Springer, 2008: 202-211.
张军男, 博士, 副研究员, 硕士生导师。主要研究方向: 流体力学和传热学。
Tel.: 025-84891160
E-mail: zhangjunrdf@nuaa.edu.cn
Numerical simulation investigation of aerodynamic interference ofsting support in wind tunnel test of a delta wing at big angles ofattack
ZHANG Jun1,*, AI Yu2, HUANG Da1, LIU Jing3
1. College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing210016, China 2. Second Research Room, Jiangnan Mechanical & Electrical Design Institute, Guiyang550009, China 3. Keppel-NUS Corporate Laboratory, Singapore City117576, Singapore
In current wars, the fighter is required to be capable of stalled flight at a high angle of attack (AOA). The investigation of the aerodynamic characteristics of the aircraft mainly relies on wind tunnel test and numerical simulation. In the wind tunnel test of high angle of attack, the commonly used method is to use sting support. The presence of the sting support can have an effect on the model testing results which will be numerically investigated in the present paper. The open source software package OpenFOAM 2.3 is used as computational fluid dynamics (CFD) computing platform, the PIMPLE algorithm is applied to solving Navier-Stokes (N-S) equations. The PIMPLE algorithm is a combination of both semi-implicit method for pressure-linked equations (SIMPLE) and pressure implicit with splitting of operator (PISO). A finite volume method is used for spatial discretization. Second order linear interpolation is also adopted. Backward differentiation method is to deal with time discretization. The employed turbulence model is Spalart-Allmaras-delayed detached eddy simulation (SA-DDES). In order to verify the reliability of the numerical method, the flow filed of the delta wing with sting support is computed at angles of attack of 0°, 10°, 30°, 50°, 70°, and 90° firstly. The obtained results are compared to the testing data and they are in close agreement. After that, the numerical simulation of the flow field of the delta wing without sting support is executed. The influence of the sting support on the flow filed, pressure coefficient distribution on the leeward side and aerodynamic coefficient is obtained through comparing the numerical results with and without sting support. In contrast to the situation without the sting support, at a high angle of attack, the presence of the sting support affects the flow field around the delta wing (but does not change the vortices and flow structure) and alters the pressure coefficient distribution on the wing leeward side. Therefore, normal force and pitching moment coefficients have significant changes.
high angle of attack; delta wing; unsteady flow field; OpenFOAM; SA-DDES; large eddy simulation
2016-01-11; Revised: 2016-02-15; Accepted: 2016-03-22; Published online: 2016-03-2516:07
National Natural Science Foundation of China (11072111)
. Tel.: 025-84891160E-mail: zhangjunrdf@nuaa.edu.cn
2016-01-11; 退修日期: 2016-02-15; 录用日期: 2016-03-22;
时间: 2016-03-2516:07
www.cnki.net/kcms/detail/11.1929.V.20160325.1607.004.html
国家自然科学基金 (11072111)
.Tel.: 025-84891160E-mail: zhangjunrdf@nuaa.edu.cn
10.7527/S1000-6893.2016.0095
V211.3
A
1000-6893(2016)08-2481-09
引用格式: 张军, 艾宇, 黄达, 等. 三角翼大迎角风洞试验支架干扰数值模拟研究[J]. 航空学报, 2016, 37(8): 2481-2489. ZHANG J, AI Y, HUANG D, et al. Numerical simulation investigation of aerodynamic interference of sting support in wind tunnel test of a delta wing at big angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2481-2489.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
URL: www.cnki.net/kcms/detail/11.1929.V.20160325.1607.004.html

