一种提高风洞动态试验数据质量的模型姿态控制和测量技术
刘志涛, 孙海生
1.西北工业大学 航空学院, 西安 710072 2.中国空气动力研究与发展中心, 绵阳 621000
一种提高风洞动态试验数据质量的模型姿态控制和测量技术
刘志涛1, 2, *, 孙海生2
1.西北工业大学 航空学院, 西安710072 2.中国空气动力研究与发展中心, 绵阳621000
低速风洞动态试验装置通常采用“电机+减速器+偏心机构+线性传动机构”的方式,存在传递环节多、机械间隙大等问题,给模型运动的精确控制和模型姿态的精确测量带来较大困难。为满足大型客机等大飞机对低速风洞动态试验的要求,基于现有的静态试验通用支撑平台,采用“电子凸轮”技术,建立了一套迎角/侧滑角解耦、可进行飞机小振幅动导数和大振幅非定常气动特性研究的动态试验装置。利用该动态试验装置进行了某飞机大尺度动态试验模型动导数试验和大振幅振荡试验,获得了试验数据的重复性,并研究了动态试验数据和静态试验数据之间的相关性。试验结果表明:利用该装置获得的某飞机动态试验数据重复性较好、规律合理,能满足大型飞机动态试验要求。
大型飞机; 动导数; 非定常气动力; 风洞试验; 支撑装置
飞机的动态气动特性(如动稳定特性和非定常气动特性)是影响飞机舒适性和安全性的重要气动因素[1]。风洞模型动导数试验和大振幅振荡试验是研究飞行器动态气动特性的两种重要试验手段,分别用于获得飞行器的动稳定特性和非定常气动特性。这两类试验的共性技术如下:利用试验支撑装置将模型置于风洞试验段中心,通过激振装置使模型绕其体轴以给定的角振幅和频率运动(如简谐振荡运动),采用角度测量传感器记录模型姿态角的时间历程,利用置于模型内部的应变天平同步测量模型所受气动载荷的时间历程。由此可见,合理的模型支撑技术、精确的模型运动控制技术和模型姿态实时高精度测量技术是决定风洞动态试验数据精准度的关键技术。
国外低速风洞配备了多种动态试验设备。比较典型的有美国NASA兰利研究中心18 m×9 m全尺寸风洞的刚性强迫振荡装置[2-5]、德国的机动振荡态天平[3,6]、法国莫当S1MA风洞的飞行力学研究装置[3,7]、瑞典航空研究院的∅3.6 m低速风洞动导数试验装置[8]、俄罗斯中央流体动力研究院在T-103等风洞开发的小振幅动导数试验系统和大振幅强迫振荡试验系统[9]。
为满足航空飞行器动态气动特性研究需求,国内空气动力试验研究机构相继开发了多种低速风洞动态试验平台。比较典型的有中国空气动力研究与发展中心低速空气动力研究所4 m×3 m低速风洞的96型动导数试验系统[10]、中国航空工业空气动力研究院FL-8风洞的动导数试验系统[11]和南京航空航天大学H-2风洞配套的动态试验系统[12]。
综观国内外低速风洞动态试验技术可以看到,大量使用了“电机+减速器+偏心机构+线性传动机构”的方式来实现试验模型所需的振荡运动:由电机驱动齿轮减速器,减速器的输出轴与偏心滑块机构相联,通过滑块机构将转动变成驱动杆的直线运动,再通过不同的支撑方式或机构分别实现模型不同的振荡运动形式,通过改变偏心滑块机构的偏心距来改变模型运动振幅。风洞试验表明[13-14],采用这种多级机械传动的方式,由于机械间隙、安装误差和级间误差传递等因素,使得试验模型的振荡运动存在较大的误差,特别是随着装置使用时间增长,机械磨损造成间隙加大,模型的运动形态与给定的运动函数偏离更大。此外,采用这种传动方式时,通常使用线位移传感器,由位移转换得到角度的方式测量模型运动角度历程,这种间接测量的方式易受机械间隙和支杆弹性变性等因素的影响,降低了模型姿态角测量精准度。另外,为协调运动振幅、驱动能力和运动控制精度之间的矛盾,大部分动态试验系统分为两套装置:小振幅动导数试验装置和大振幅振荡试验装置,增大了动导数试验数据和大振幅振荡试验数据之间的相关性误差。传统的风洞动态试验系统多采用风洞转盘转角和模型支杆滚转角组合的方式获得模型的迎角和侧滑角,这种方式不足之处为:① 支撑装置偏离风洞中心,模型相对于风洞风轴系存在一个滚转角,使得试验过程中模型常常处于不对称的来流条件和边界条件下,给动态试验数据的准度带来一定影响;② 不便于开展迎角和侧滑角的组合试验,试验效率较低。
为克服传统的动态试验系统采用“电机+减速器+偏心机构+线性传动机构”传动方式存在的不足,提高动态试验数据的精准度,设计了采用风洞静态支撑装置为基础支撑平台来实现模型的初始姿态(迎角、侧滑角)、可编程电机/减速器的驱动方式实现模型的振荡运动(俯仰、偏航和滚转)的动态试验方案,实现了迎角/侧滑角解耦、振幅范围宽且可无级调节的功能。在此基础上,提出了与系统相匹配的模型姿态与气动载荷高精度测量方案。利用一种大展弦比飞机大尺度模型对本文建立的动态试验技术进行了验证,考核了系统的动导数试验和大振幅振荡试验能力。
1 动态试验装置
1.1支撑平台
图1给出了一种典型的低速风洞动态试验系统支撑装置示意图[15]。采用这种支撑方式时,模型的初始迎角和侧滑角由风洞转盘转角和模型支杆滚转角组合获得,由于风洞洞壁的存在,使得试验过程中模型常常处于不对称的来流条件和边界条件下,影响了动态试验数据的准度。为实现模型迎角、侧滑角解耦,本文介绍的动态试验系统以风洞静态支撑装置(见图2)为支撑平台[16],该支撑装置的变角度机构通过2个迎角伺服油缸、1个y向油缸及4个前、后侧滑角伺服油缸驱动,可实现模型迎角与侧滑角的变化及组合,且模型迎角和侧滑角机构互相独立(见图3)。
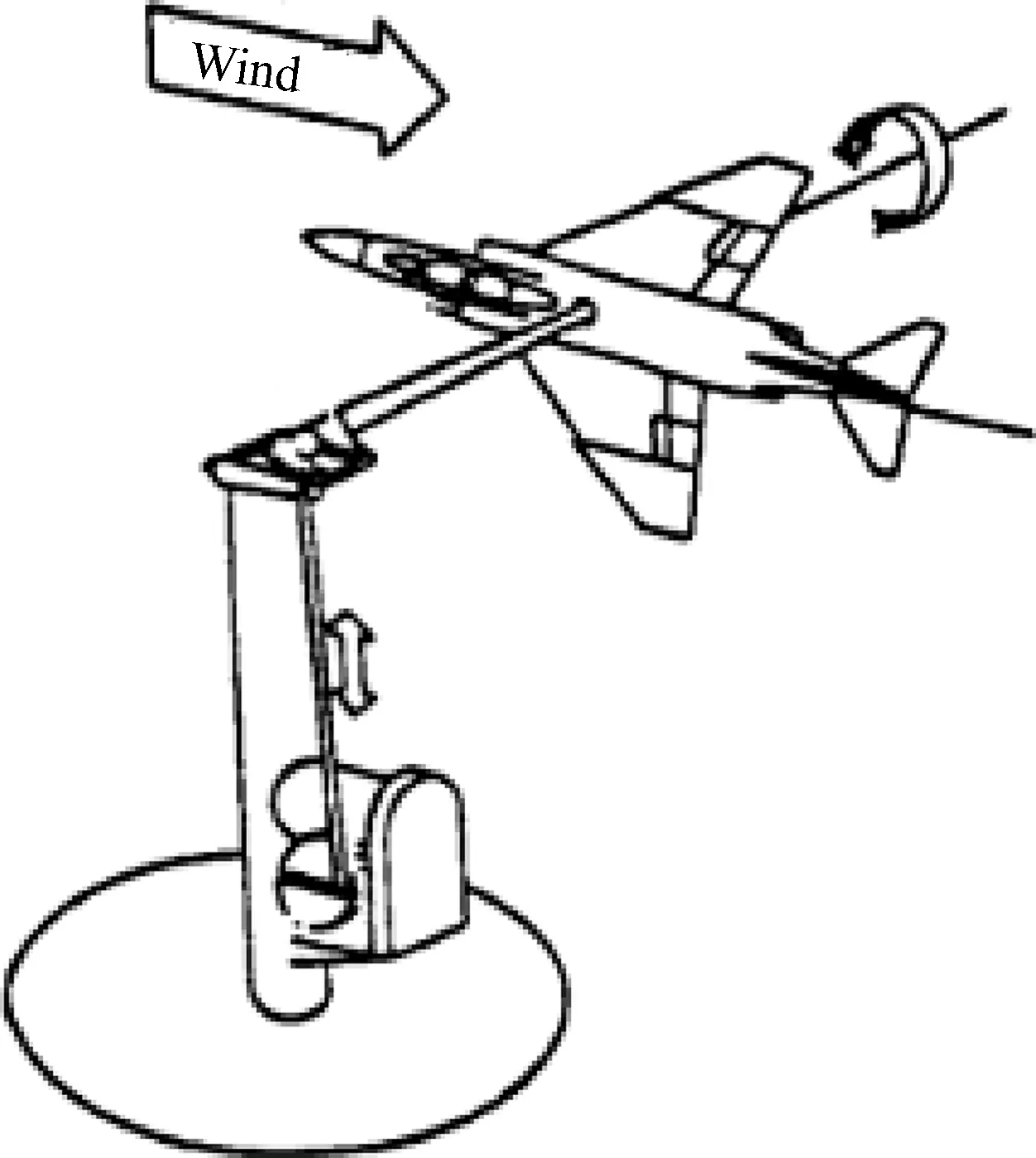
图1 传统的动态支撑装置Fig.1 Normal dynamic support rig
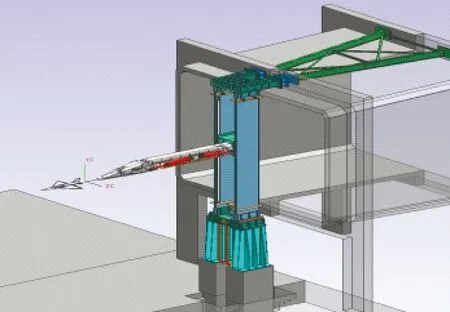
图2 8 m×6 m风洞静态支撑装置Fig.2 Static support rig in 8 m×6 m wind tunnel
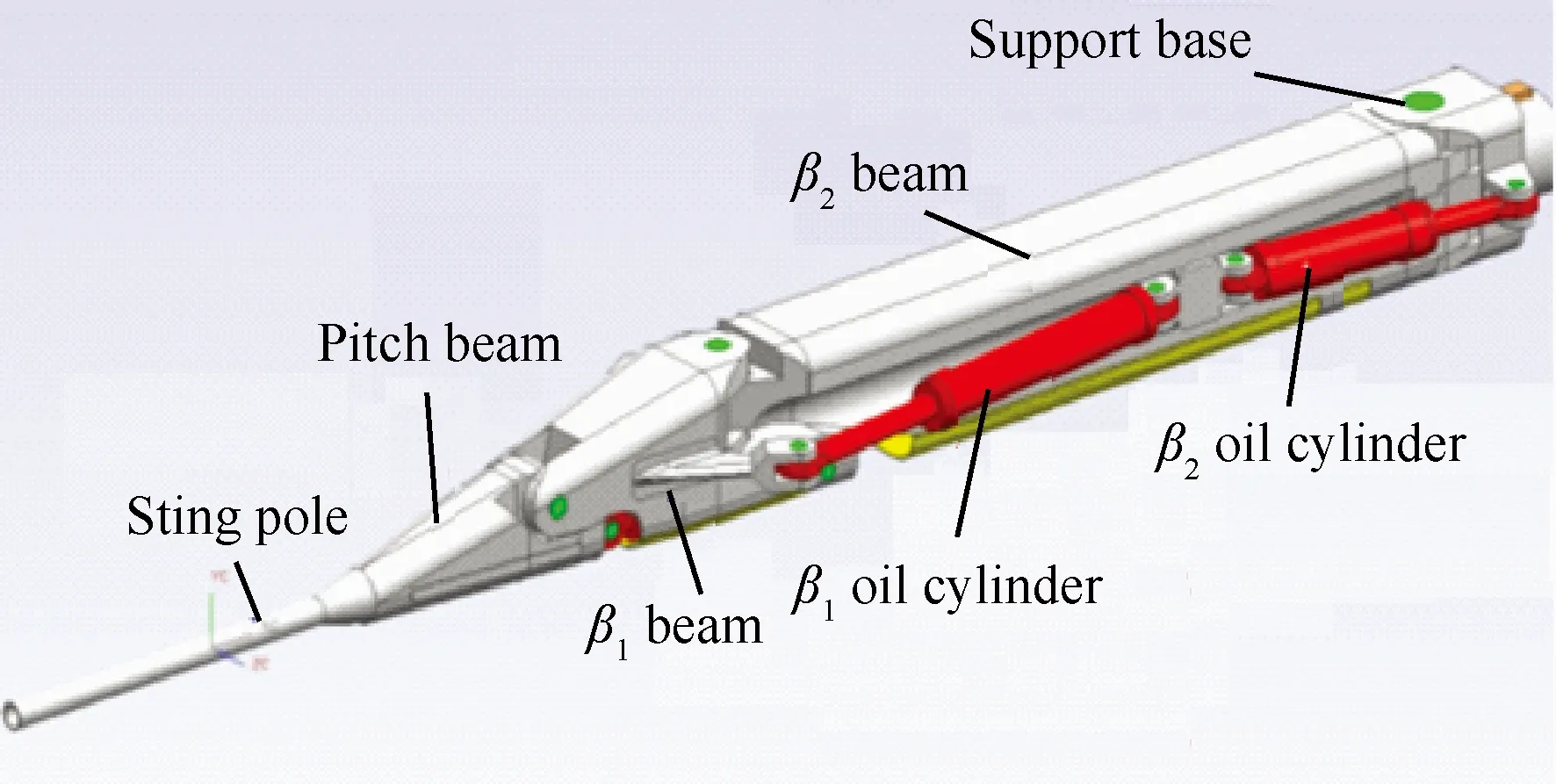
图3 α、β机构示意图Fig.3 Schematic of α、β mechanism
1.2激振机构
激振机构用于实现模型的振荡运动,由运动驱动机构和运动传递机构组成。在激振方式上,采用可编程电机,引入“电子凸轮”技术,建立了基于“伺服电机+减速器+运动控制器”的振荡系统,即通过程序控制实现电机按照给定规律转动(简谐振荡或其他给定函数),电机转动运动经减速器转换后,作用于模型支杆进而直接驱动飞行器模型实现所需的振荡运动。该系统结构简单,振荡波形、幅值和频率程控可调,减少了传动环节,减小了传动间隙和支撑装置几何尺寸。
下面以俯仰振荡运动为例对激振机构的关键设计点进行说明。
俯仰振荡的运动传递机构采用平行四边形机构,如图4所示。试验模型采用腹撑或背撑形式,由俯仰主支杆、摇臂、俯仰尾支杆和天平套筒组成平行四边形机构(见图5)。电机和减速器驱动摇臂转动,摇臂带动尾支杆上下运动,尾支杆另一端与天平套筒相连从而驱动模型实现俯仰振荡。电机处的关节为始动力关节,减速器轴与轴套为键连接,轴套与摇臂之间的胀紧套在胀开后使两个转动固定,以使摇臂随减速器轴转动(见图6)。运动关节处均采用滚动轴承支撑。
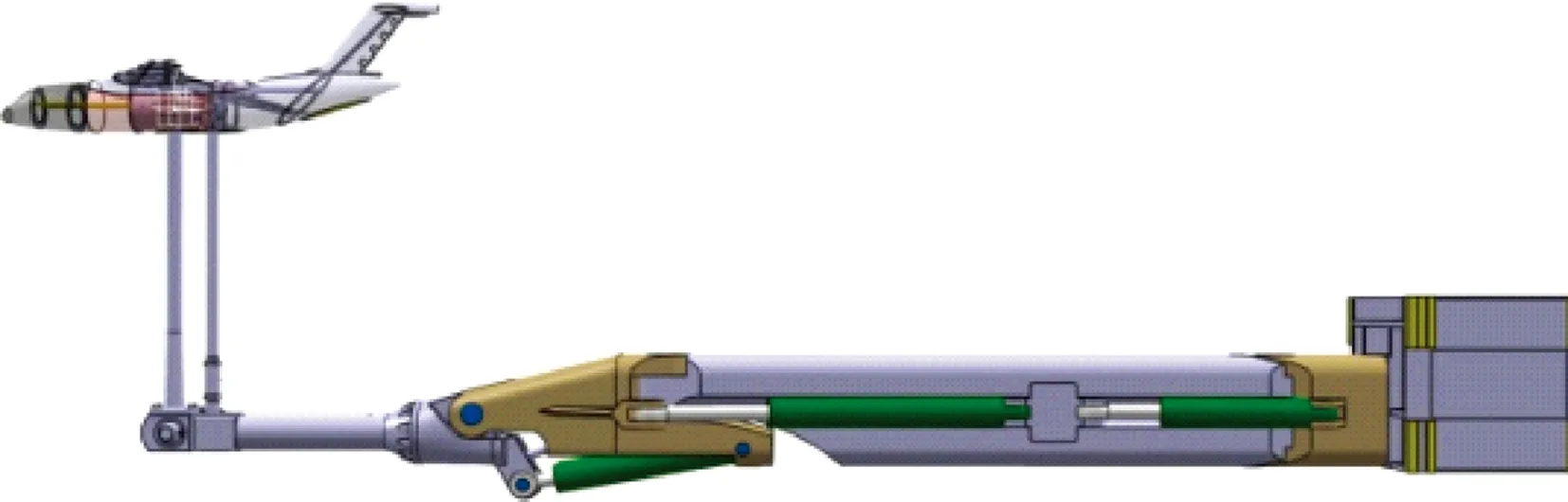
图4 俯仰振荡装置示意图Fig.4 Schematic of pitching oscillation rig
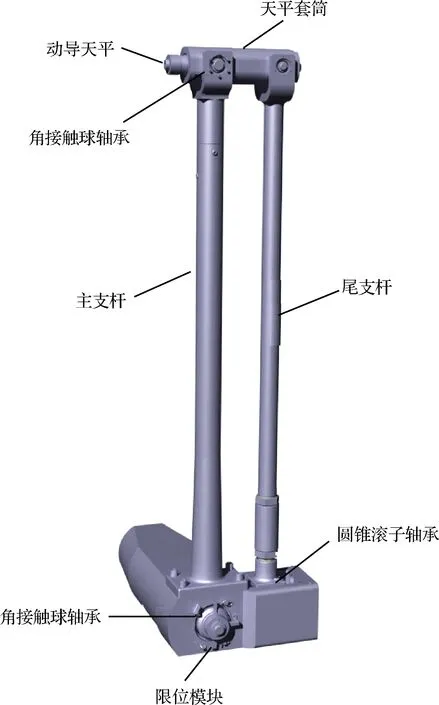
图5 俯仰运动机构Fig.5 Pitching motion mechanism
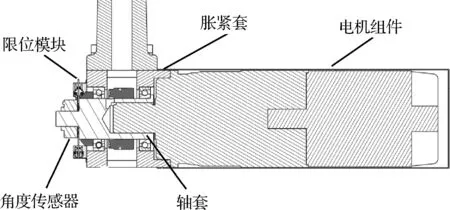
图6 电机装配示意图Fig.6 Schematic of electric motor installation
减小运动关节处的间隙对于动态激振机构而言非常重要。为此,选用精密级行星齿轮减速器,使减速器转动中心的回程间隙小于5 arcmin(弧分)。摇臂与尾支杆的铰接精度采用5级精度的轴承来保证。对于天平套筒上的两个铰接点,由于其位于模型内部,在尽可能减小外形尺寸的前提下如何保证其旋转精度就非常重要。通过对比各种转动连接方式,这两个铰接点最终选用滑动连接方式。此外,为保证转动精度,滑动面选用专用轴套,轴套材料选用ZCuSn10Pb1,具有硬度高、耐磨性极好的特点,不易产生咬死现象,有较好的铸造性能和可加工性,适合于高负荷和高滑动速度下工作的耐磨件。
对于俯仰振荡机构,综合考虑模型的机身尺寸、天平的刚度和灵敏度、近场及远场支架干扰、结构强度和变形等因素,对平行四边形机构几何尺寸进行优化设计。
偏航振荡机构如图7所示。模型采取腹部单点支撑方式,电机固定在减速器上,减速器固定在连接支杆上,减速器输出轴与偏航支杆固连,通过自动控制交流伺服电机直接驱动支杆转动的方式,实现模型的偏航振荡运动。利用上下两个圆锥滚子轴承将偏航支杆固定到整流罩上,消除了偏航支杆除轴向转动以外的其他自由度。为保证偏航支杆旋转时的精度并降低旋转时的阻尼,两个轴承选用5级精度的32917轴承。
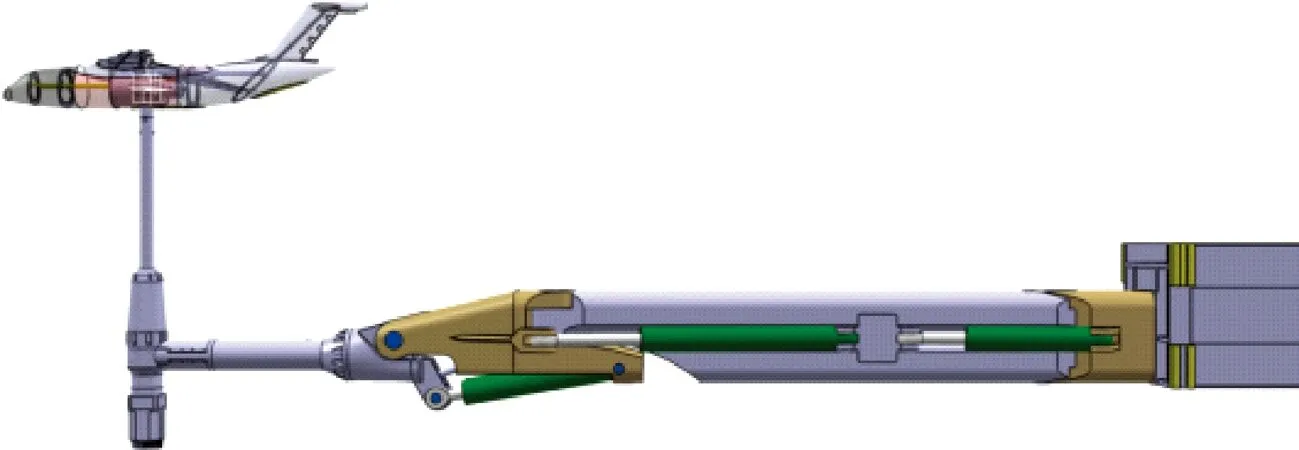
图7 偏航振荡装置示意图Fig.7 Schematic of yawing oscillation rig
滚转和偏航振荡共用一套部件,通过更换与通用支撑装置相连接的接头及天平套筒,可实现模型的滚转振荡运动(见图8)。模型采取尾撑方式,利用过渡支杆将模型抬高,以减小远场支架对模型尾迹的干扰。
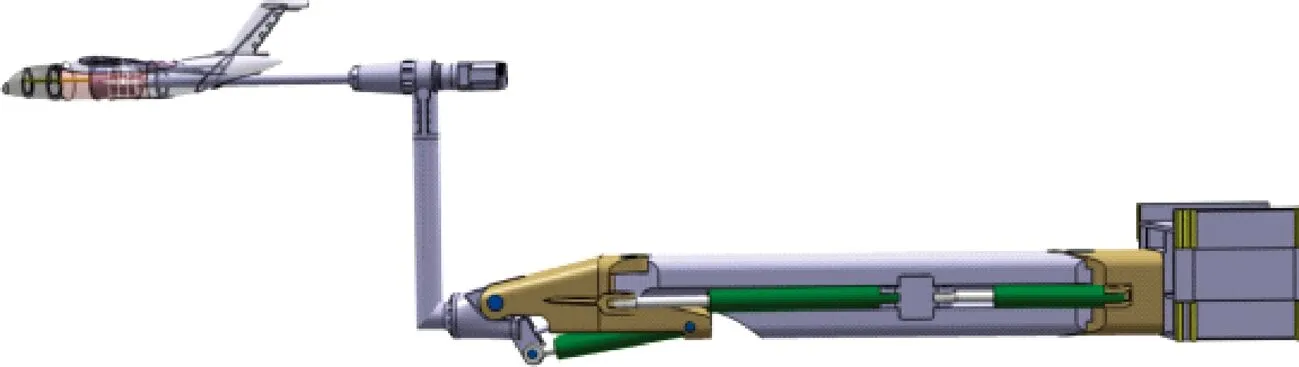
图8 滚转振荡装置示意图Fig.8 Schematic of rolling oscillation rig
1.3控制系统
控制系统主要用于控制运动机构驱动模型按给定规律运动,可实现简谐振荡运动或其他任意设定的单自由度角运动,以满足动导数、大振幅振荡等试验要求。
控制系统采用“IPC+运动控制器+交流伺服”的组成方式,整体结构如图9所示,主要元件包括上位机、运动控制器、伺服驱动器、伺服电机、编码器和电位计。运动控制器主要完成运动轨迹生成和位置闭环控制,将伺服电机上的编码器作为速度环的反馈,并结合安装在运动部件终端的高精度角位移传感器,构成位置和速度的全闭环控制系统:伺服驱动器接收速度指令,完成速度环的控制;运动控制器完成位置环的控制,并对机械传动上的间隙误差进行补偿,进而实现高精度的位置控制。
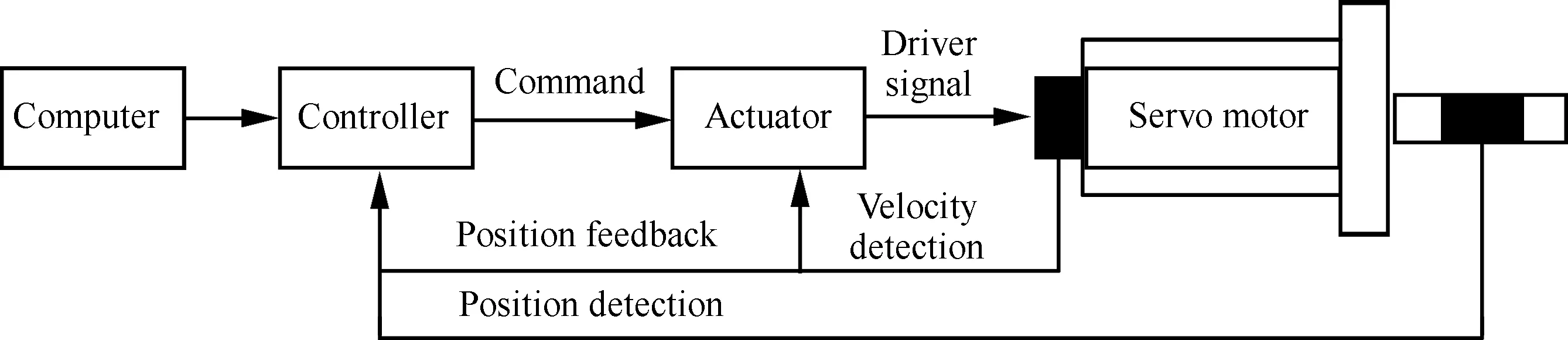
图9 控制系统结构框图Fig.9 Block diagram of control system structure
图10和表1、表2给出了运动控制系统测试结果。图10为俯仰振荡振幅为10°、频率为 1 Hz 时的幅频特性。表1和表2分别为无风载和带风载条件下振荡运动模拟准确度数据。可知,动态试验系统实现的模型运动波形失真非常小,运动频率与振幅的控制精度和准度均较高。

图10 俯仰振荡振幅10°、频率1 Hz时的幅频特性Fig.10 Amplitude and frequency characteristics(pitching oscillation, amplitude is 10°, frequency is 1 Hz)
表1 无风载条件下振荡运动模拟准确度数据表
Table 1Data sheet of accuracy of oscillation motion simulation without wind load

Ampli-tude/(°)Frequ-ency/HzErrorofamplitude/(')Distortionofangu-lardisplacement/10-4Distortionofangularrate/10-4100.5<21.0241.316102.0<31.0151.165
表2带风载条件下振荡运动模拟准确度数据表
Table 2Data sheet of accuracy of oscillation motion simulation with wind load

Ampli-tude/(°)Frequ-ency/HzErrorofamplitude/(')Distortionofangu-lardisplacement/10-4Distortionofangularrate/10-4100.5<11.0271.313
2 测量和数据处理
2.1气动载荷测量
动态天平要求具有良好的动态响应特性,天平设计时最重要的设计点是刚度。刚度不足将限制最高振荡频率,或使振荡振幅与相位失真产生大的误差,因此在满足天平精度要求的情况下需尽量提高天平的刚度。天平结构如图11所示,采用3个措施以提高动态天平的刚度:① 采用“T”型元件形式,在与“I”型元件获得相同输出的情况下,采用这种元件形式可使刚性提高一倍;② 增加阻力元件辅助支撑片数量,同时采用变截面和长度布局辅助支撑片的方式提高刚性;③ 改变阻力元件切槽方式(见图12),把两侧辅助支撑片和天平体连为整体,有效地增强了刚性,并减小了分量间的相互干扰。此外,在保证天平刚度的前提下,为提高天平的灵敏度,天平阻力梁采用等强度梁的形式。即阻力梁“T”型测量元件设计采用等强度梁结构形式,避免了应力集中和应力变化梯度过大的问题,降低了应变计粘贴位置对天平灵敏度的影响;辅助支撑片也采用等强度梁方式,改善了应力集中而导致的刚性降低问题,增加了测量主梁的载荷分配,达到了增强整体刚性的同时提高阻力分量灵敏度的效果。表3给出了天平各分量之间的干扰比例(x、y、z、Mx、My、Mz分别表示天平轴系的三个方向的力和力矩)。可知,各分量之间的干扰比例很小,天平具有良好的动态响应特性。
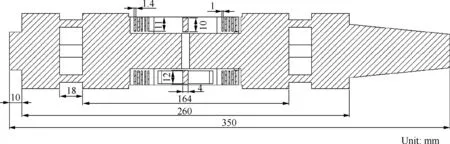
图11 天平结构示意图Fig.11 Schematic of balance structure
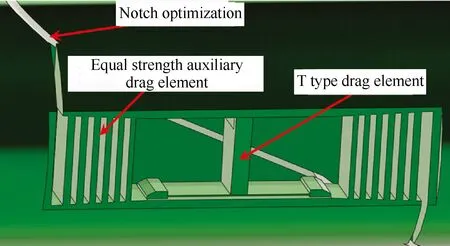
图12 天平刚度优化设计Fig.12 Balance stiffness optimization design
表3 天平各分量之间干扰比例
Table 3Proportion of interference between different
balance units

ComponentyxMzzMyMxProportionofinterference/%0.52.51.82.92.44.7
2.2模型姿态测量
动态试验模型姿态的精确测量是获得准确的动态试验数据的关键技术。传统的基于“电机+减速器+偏心机构+线性传动机构”驱动方式的动态试验系统,通常采用线位移传感器记录线性传动机构的位置,通过转换计算得到模型姿态角,测量端距运动终端(模型)较远,由于机构间隙和支撑装置结构变形,测量结果存在较大误差。近年来,光学测量技术在风洞试验模型姿态测量中的应用越来越受到重视,如基于视频模型变形(Video Model Deformation, VMD)技术的双(多)目图像处理的模型姿态角测量技术[17]、基于三线阵CCD数字图像处理技术的Optotrak模型姿态测量技术[18]等。VMD技术的不足之处为:图像处理相对复杂,计算量大,实时性较差,不能满足动态试验模型姿态测量的实时性要求。Optotrak模型姿态测量技术具有测量精准度高(直接测量模型的姿态)、实时性强和可外同步测量等特点,但其不足之处为:需要在模型表面布设标志点,对模型表面外形存在一定影响。若将标志点内埋,则对模型制作要求较高。综合以上因素,结合本文动态试验系统采用“伺服电机+减速器+运动控制器”驱动方式的技术特点,采取安装在运动机构末端、与模型旋转运动轴同轴的高精度角位移传感器实时测量模型姿态角。考虑到角位移传感器未安装于模型内部,支杆和天平套筒之间的间隙、天平的弹性变形等会给测量结果带来误差,本文将高精度角位移传感器测量结果和Optotrak模型姿态测量结果进行了对比,验证了这种测量方法的可靠性。针对一种俯仰振荡运动,采用这两种方法对模型姿态进行同步测量,图13和表4给出了俯仰振荡装置角测量结果的对比。
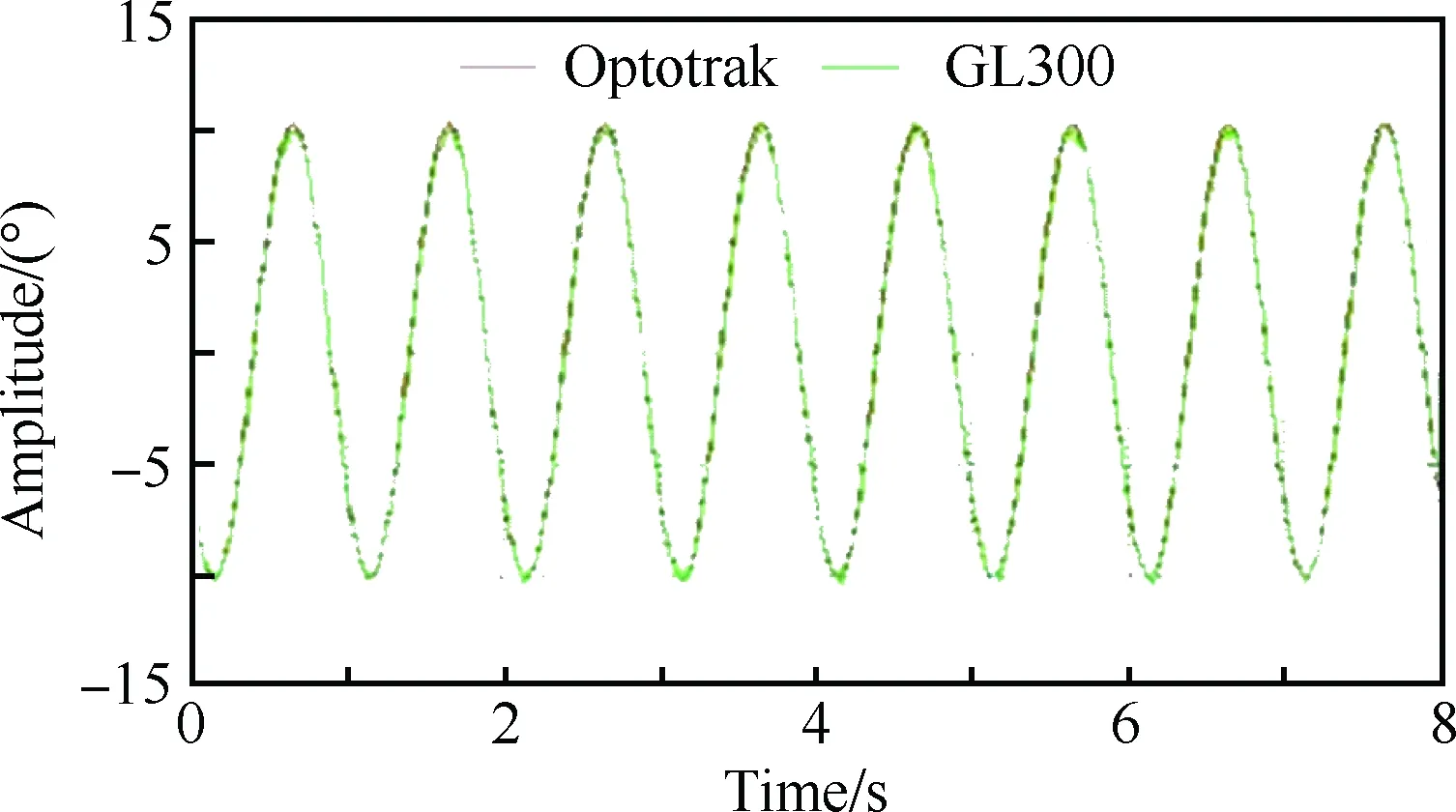
图13 Optotrak和GL300的俯仰振荡角测量对比结果Fig.13 Comparison of pitching oscillation angle measurement results between Optotrak and GL300
2.3信号处理
采用最优的小信号分离检测技术[19-20]对动态信号进行预处理,将天平信号中微弱的有效信号分离出来。一是去趋势项,按周期平均及消除平均值项得到只有交变成分的角位移和天平信号;二是通过数字滤波,将位移和天平信号转换成频率信号,进行处理后再应用傅里叶反变换将频域信号还原为时域信号。由于角位移与天平信号之间的相位差对于动导数的计算至关重要,本文采用高精度的全相位傅里叶变换(APFFT)法,求取各个信号的相位。图14显示了两类振荡方式时,3种不同方法计算得到的关键动导数重复性精度。可以看到,3种方法计算的重复性精度相差不大,在小角度范围内,俯仰和滚转振荡,使用全相位傅里叶变换的频域对齐方法,精度略有提高。
表4Optotrak和GL300的俯仰振荡角测量结果
Table 4Pitching oscillation angle measurement results of Optotrak and GL300
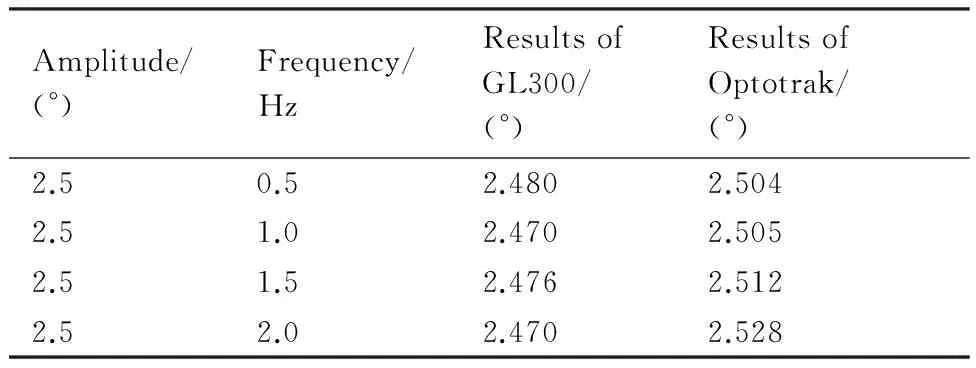
Amplitude/(°)Frequency/HzResultsofGL300/(°)ResultsofOptotrak/(°)2.50.52.4802.5042.51.02.4702.5052.51.52.4762.5122.52.02.4702.528

图14 阻尼导数重复性精度Fig.14 Damping derivative repeatability accuracy
3 典型试验结果
3.1动导数试验结果
3.1.1重复性试验结果
表5给出了某飞机模型巡航构型下7次重复性动导数试验的均方根误差,表6给出了动导数的相对精度。表中:α为迎角。相对精度定义为试验数据的1.5倍均方根误差与其算术平均值之比。
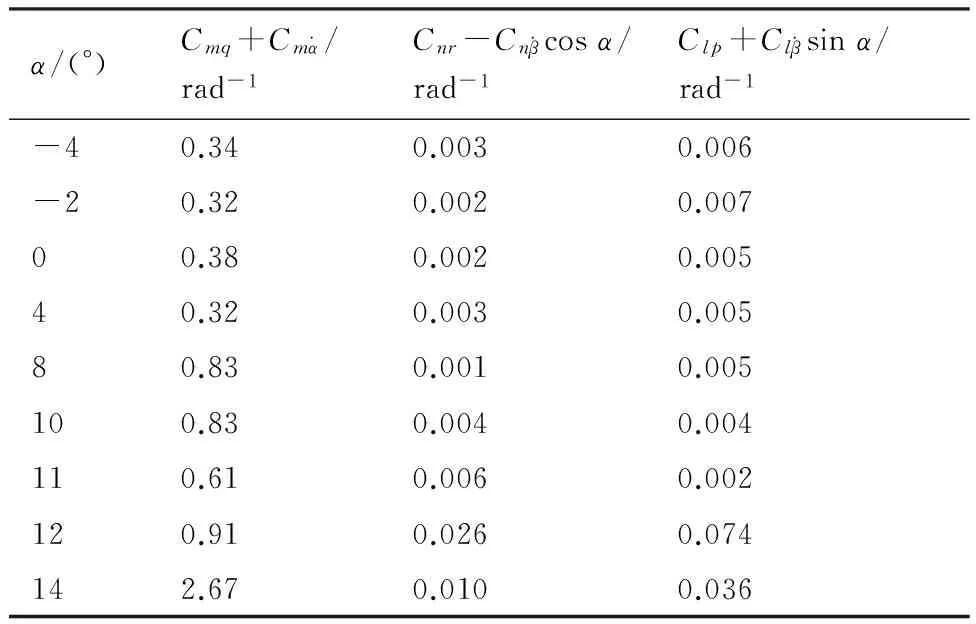
表5 动导数均方根误差
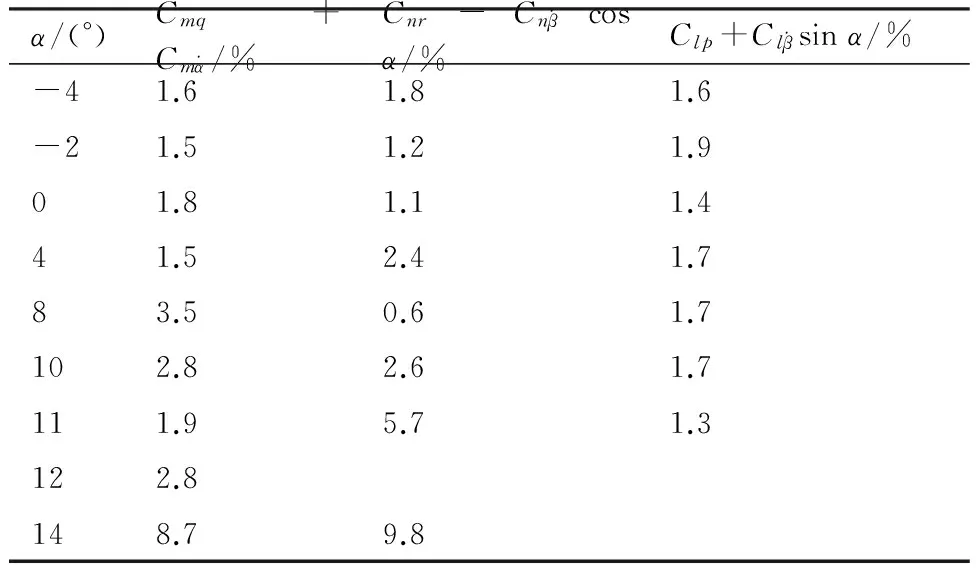
表6 动导数相对精度
国外动导数试验数据的重复性精度可达5%[21-22],国内动导数试验数据的重复性精度在10%左右[14]。
3.1.2静、动态试验结果相关性研究
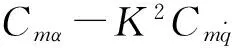
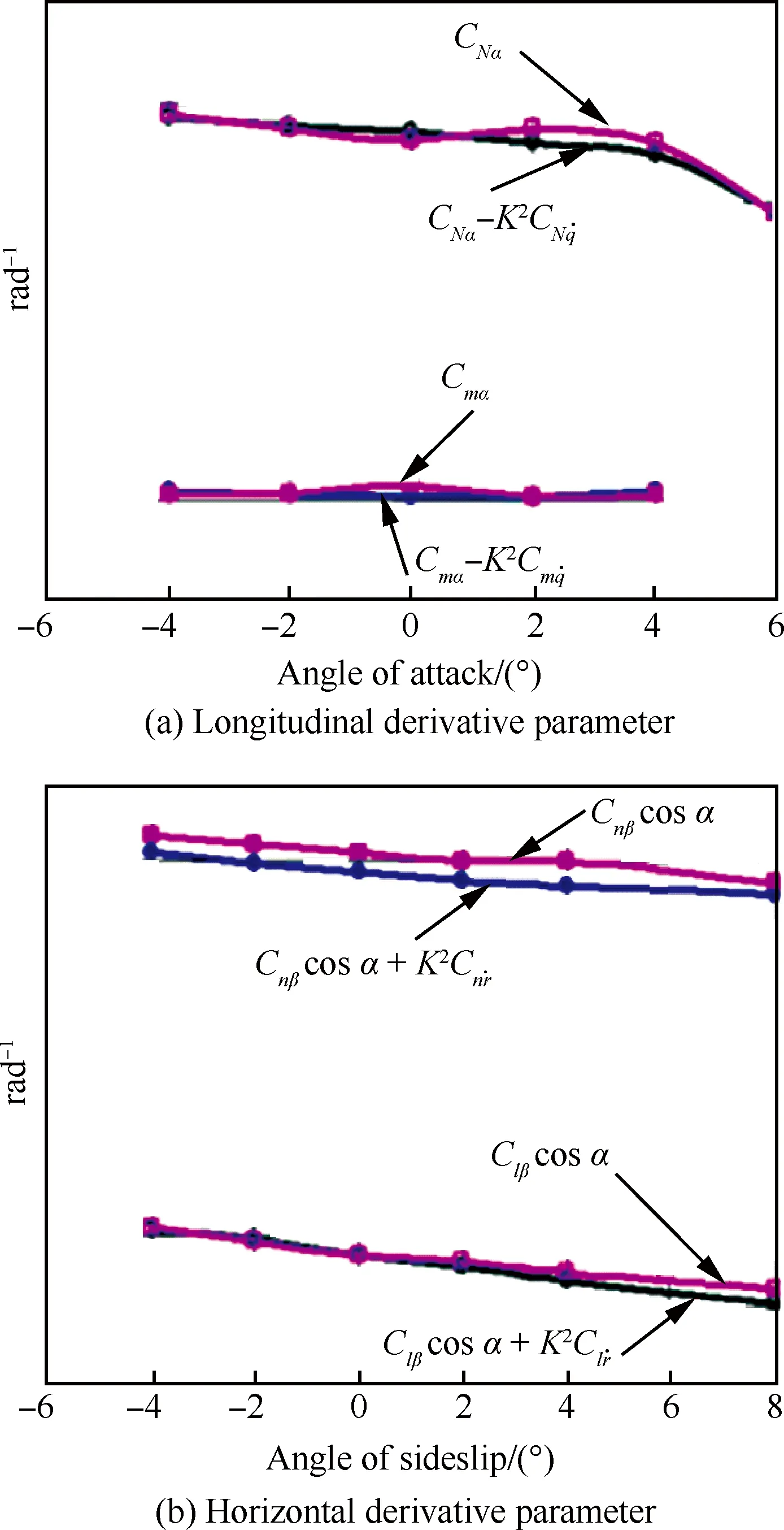
图15 静态和动态试验结果的相关性(巡航构型)Fig.15 Relativity for static and dynamic test results (cruise configuration)
3.2大振幅振荡试验结果
3.2.1重复性试验结果
表7~表9给出了某飞机模型巡航构型下大振幅振荡试验数据的重复性精度(7次重复性试验数据的均方根误差)。表中:CN为法向力系数;Cm为俯仰力矩系数;Cn为偏航力矩系数;Cl为滚转力矩系数。可见,3种振荡运动模式下,大振幅振荡试验数据的重复性精度接近静态测力试验国军标指标要求,即大振幅振荡试验数据具有很高的重复性精度。
表7大振幅俯仰振荡试验数据均方根误差
Table 7Root-mean-square error of large amplitude pitching oscillation test results

Pitchingangle/(°)σCNσCm00.00320.003850.00150.0016100.00210.0010150.00230.0012200.00230.0015
表8大振幅偏航振荡试验数据均方根误差
Table 8Root-mean-square error of large amplitude yawing oscillation test results
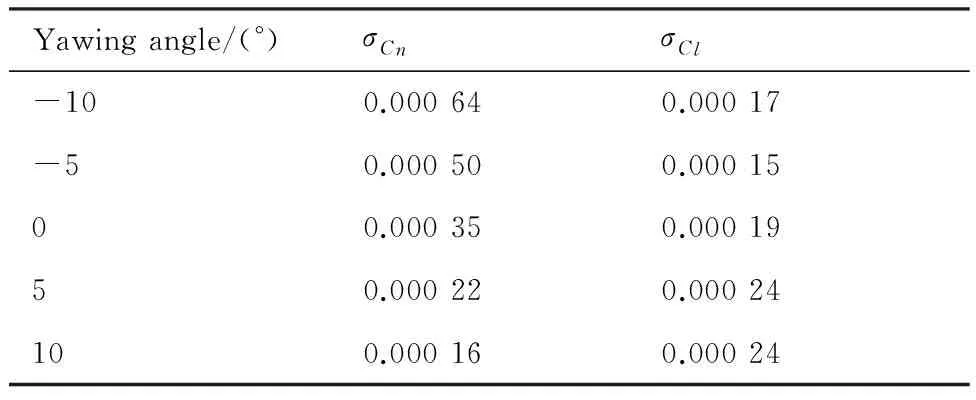
Yawingangle/(°)σCnσCl-100.000640.00017-50.000500.0001500.000350.0001950.000220.00024100.000160.00024
表9大振幅滚转振荡试验数据均方根误差
Table 9Root-mean-square error of large amplitude rolling oscillation test results
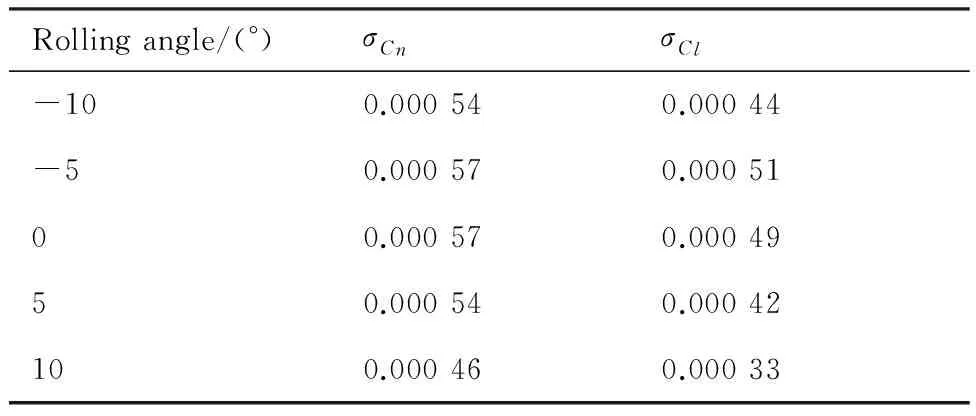
Rollingangle/(°)σCnσCl-100.000540.00044-50.000570.0005100.000570.0004950.000540.00042100.000460.00033
3.2.2平衡角对非定常气动特性的影响
图16给出了不同平衡角下俯仰振荡试验结果。可知,平衡角对俯仰振荡非定常气动特性影响较大:平衡角越大,气动力迟滞环面积越大,非定常效应越明显。不同平衡角下获得的气动力迟滞环衔接较好,静态气动力曲线基本位于动态气动力迟滞环内。以上结果表明,动态试验系统获得的大振幅振荡试验数据规律良好。
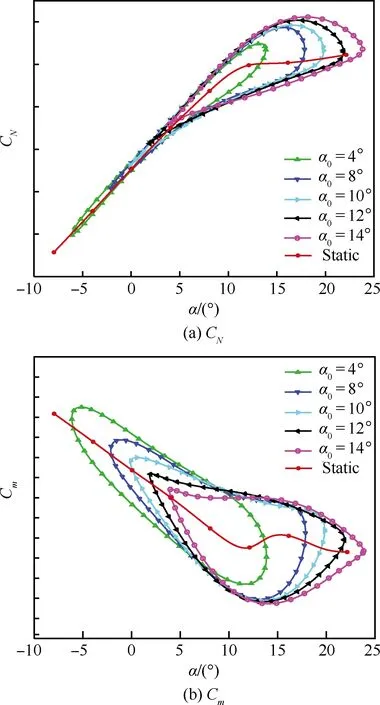
图16 俯仰振荡非定常气动力曲线(频率1 Hz,振幅10°)Fig.16 Unsteady aerodynamic curves at pitching oscillation (frequency is 1 Hz,amplitude is 10°)
4 结 论
1) 针对传统低速风洞动态试验系统存在的不足,引入“电子凸轮”技术,采用“伺服电机+减速器+运动控制器”的风洞动态试验模型振荡运动驱动模式和速度、位置双闭环控制策略,高精度角位移传感器和Optotrak光学测量相结合的模型姿态实时精确测量技术,高刚度高灵敏度天平技术建立的低速风洞动态试验平台,在一套系统上建立了动导数试验和大振幅振荡试验能力,具有迎角/侧滑角解耦、运动频率高、振幅范围宽且可无级调节及运动控制精度高等特点。
2) 利用本文介绍的动态试验技术获得的动态试验数据具有良好的精准度。某飞机大尺度动态试验模型动导数和大振幅振荡试验结果表明,动导数试验数据的重复性精度与国外先进水平相当,大振幅振荡试验数据的重复性精度接近静态测力试验国军标合格指标。动态试验数据与静态试验数据之间的相关性良好,动态气动特性随振荡平衡角等参数变化规律合理。
3) 本文建立的基于“电子凸轮”的动态试验驱动技术、模型姿态实时测量技术和高刚度天平技术等对于相关的风洞试验技术具有较强的参考价值。
[1]LAN C E, WU K Y, YU J. Flight characteristics analysis based on QAR data of a jet transport during landing at a high-altitude airport[J]. Chinese Journal of Aeronautics, 2012, 25(1): 13-24.
[2]North Atlantic Treaty Organization. Dynamic stability parameters: AGARD-CP-235[R]. London: Technical Editing and Reproduction Ltd., 1978.
[3]North Atlantic Treaty Organization. Dynamic stability parameters: AGARD-LS-114[R]. London: Technical Editing and Reproduction Ltd., 1981.
[4]GRAFTON S B. Dynamic stability derivatives of a twin-jet fighter model for angles of attack from -10° to 110°: NASA TN D-6091[R]. Hampton: Langley Research Center, 1971.
[5]OWENS D B, BRANDON J M, CROOM M A, et al. Overview of dynamic test techniques for flight dynamics research at NASA LaRC: AIAA-2006-3146[R]. Reston: AIAA, 2006.
[6]ALTENKIRCH D. Flight mechanics analysis of the dynamic derivatives of the Dornier variable wind tunnel model: ESA-TT-854[R]. Hampton: Langley Research Center, 1984.
[7]CHRISTOPHE J. New rig for flight mechanics studies: AIAA-1980-0464[R]. Reston: AIAA, 1980.
[8]JANSSON T, TORNGREN L. New dynamic testing technique and related results at FFA: AD-P005024[R]. Goteborg: The Aeronautical Research Institute of Sweden, 1983.
[9]GOMAN M G, GREENWELL D I, KHRABROV A N. The characteristic time constant approach for mathematical modeling of high angle of attack aerodynamics[C]//ICAS 2000 Congress, 2000.
[10]孙海生. 96型低速大攻角动导数试验系统[J]. 流体力学实验与测量, 1999, 13(1): 31-37.
SUN H S. The development of 96-test system for measuring dynamic derivatives at high angle of attack[J]. Experiments and Measurements in Fluid Mechanics, 1999, 13(1): 31-37 (in Chinese).
[11]卜忱, 杜希奇, 王学俭. 飞行器纵向阻尼动导数直接测量实验研究[J]. 实验流体力学, 2005, 19(1): 31-34.
BU C, DU X Q, WANG X J. Investigation of longitudinal damping derivative of aircraft by direct measurement tests[J]. Experiments and Measurements in Fluid Mechanics, 2005, 19(1): 31-34 (in Chinese).
[12]史志伟, 吴根兴. 大迎角非定常气动力建模与模型比较[J]. 空气动力学学报, 1999, 17(4): 454-461.
SHI Z W, WU G X. The comparison of several unsteady aerodynamics models at high angle of attack[J]. Acta Aerodynamica Sinica, 1999, 17(4): 454-461 (in Chinese).
[13]孙海生. 飞行器大迎角非定常气动力试验研究[D]. 西安: 西北工业大学, 2011.
SUN H S. Experimental study on unsteady aerodynamics of aircraft at high angle of attack[D]. Xi’an: Northwestern Polytechnical University, 2011.
[14]李周复. 风洞特种实验技术[M]. 北京: 航空工业出版社, 2010: 249.
LI Z F. The special experimental technology in wind tunnel[M]. Beijing: Aviation Industry Press, 2010: 249 (in Chinese).
[15]GRAFTON S B, PARLETT L P, CHARLES C S. Dynamic stability derivatives of a jet transport configuration with high thrust-weight ratio and an externally blown jet flap: NASA TN D-6440[R]. Hampton: Langley Research Center, 1971.
[16]孙海生, 张晖, 汤更生, 等. 8 m×6 m风洞特大迎角试验设备研制[J]. 实验流体力学, 2009, 23(1): 70-73.
SUN H S, ZHANG H, TANG G S, et al. The development of high angle of attack test equipment in the 8 m×6 m low speed wind tunnel[J]. Experiments and Measurements in Fluid Mechanics, 2009, 23(1): 70-73 (in Chinese).
[17]张征宇, 喻波, 黄诗捷, 等. 风洞试验中模型迎角的视频测量及精度研究[J]. 实验流体力学, 2013, 27(1): 88-90.
ZHANG Z Y, YU B, HUANG S J, et al. Videogrammetric measurement of attack angle and its precision investigation in wind tunnel tests[J]. Experiments and Measurements in Fluid Mechanics, 2013, 27(1): 88-90 (in Chinese).
[18]顾艺, 岑飞, 温渝昌, 等. 基于非接触测量技术的低速风洞连续扫描试验技术研究[J]. 实验流体力学, 2013, 27(5): 98-104.
GU Y, CEN F, WEN Y C, et al. Research about continuous scanning test technique based on non-contact measurement technique in low speed wind tunnel[J]. Experiments and Measurements in Fluid Mechanics, 2013, 27(5): 98-104 (in Chinese).
[19]章克来, 朱海明. 微弱信号检测技术[J]. 航空电子技术, 2009, 40(2): 30-36.
ZHANG K L, ZHU H M. Weak signal detection technology[J]. Avionics Technology, 2009, 40(2): 30-36 (in Chinese).
[20]彭长英, 沈志洪, 段丕轩. 动导数试验数据测量与处理系统[C]//全国空气动力测控技术会, 2005.
PENG C Y, SHEN Z H, DUAN P X. Development of measurement and data processing system for dynamic derivative test[C]//Chinese Aerodynamics Experimental Measurement and Control Technology Conference, 2005 (in Chinese).
[21]North Atlantic Treaty Organization. Cooperative programme on dynamic wind tunnel experiments for manoeuvring aircraft: AGARD-AR-305[R]. Hull: Canada Communication Group, 1996.
[22]DAN D V, THOMOS D L, ANDRES S. SACCON forced oscillation tests at DNW-NWB and NASA Langley 14×22-foot tunnel: AIAA-2010-4394[R]. Reston: AIAA, 2010.
刘志涛男, 硕士, 副研究员。主要研究方向: 大攻角空气动力学。
Tel.: 0816-2461906
E-mail: liuzhitao@cardc.cn
孙海生男, 博士, 研究员, 博士生导师。主要研究方向: 非定常空气动力学。
Tel.: 0816-2461001
E-mail: sunhaisheng@cardc.cn
A model attitude control and measurement technique for improving quality of wind tunnel dynamic test data
LIU Zhitao1, 2, *, SUN Haisheng2
1. School of Aeronautics, Northwestern Polytechnical University, Xi’an710072, China 2. China Aerodynamics Research and Development Center, Mianyang621000, China
Motors, reducers, eccentric mechanisms and linear linkage mechanisms combination is commonly adopted by dynamic test equipment in a low speed wind tunnel. The derived problems such as too many linkages and too large mechanical clearance will lead to difficulties in precise control of model motion and model attitude measurement accuracy. A dynamic test equipment employing programmed motor technique is developed to meet the requirements of large transport airplanes for low speed wind tunnel dynamic tests based on the available generic support platform for static tests which can be used for small amplitude dynamic derivatives and large amplitude unsteady aerodynamic characteristics study on a aircraft. The dynamic derivative and large amplitude oscillation tests on some large scaled aircraft model are carried out to acquire the data repeatability and investigate the correlation between dynamic data and static data. Test results indicate that the good repeatability and reasonable change law abstracted from the aircraft dynamic test data can fulfill the demands of large aircraft dynamic tests.
large aircraft; dynamic derivatives; unsteady aerodynamics; wind tunnel test; support rig
2016-02-17; Revised: 2016-03-10; Accepted: 2016-05-23; Published online: 2016-06-0708:30
. Tel.: 0816-2461906E-mail: liuzhitao@cardc.cn
2016-02-17; 退修日期: 2016-03-10; 录用日期: 2016-05-23;
时间: 2016-06-0708:30
www.cnki.net/kcms/detail/11.1929.V.20160607.0830.002.html
.Tel.: 0816-2461906E-mail: liuzhitao@cardc.cn
10.7527/S1000-6893.2016.0155
V211.7
A
1000-6893(2016)08-2426-10
引用格式: 刘志涛, 孙海生. 一种提高风洞动态试验数据质量的模型姿态控制和测量技术[J]. 航空学报, 2016, 37(8): 2426-2435. LIU Z T, SUN H S. A model attitude control and measurement technique for improving quality of wind tunnel dynamic test data[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2426-2435.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
URL: www.cnki.net/kcms/detail/11.1929.V.20160607.0830.002.html
———重庆建成世界一流汽车风洞

