非结构变形网格和离散几何守恒律

刘君， 刘瑜， 陈泽栋

1.大连理工大学 航空航天学院， 大连　116024 2.装备学院 航天装备系， 北京　101416 3.大连理工大学 工程力学系， 大连　116024



非结构变形网格和离散几何守恒律

刘君1,*， 刘瑜2， 陈泽栋3

1.大连理工大学 航空航天学院， 大连116024 2.装备学院 航天装备系， 北京101416 3.大连理工大学 工程力学系， 大连116024

数值模拟流固耦合问题或多体分离问题的非定常流动时，常采用基于任意拉格朗日-欧拉(ALE)方程的有限体积法，涉及到变形网格和离散几何守恒律。在对变形网格算法进行综述时，按照构造思想分为物理比拟、椭圆光顺、插值、运动子网格(MSA)及其混合法共5类，分别介绍了基本原理、研究现状和适用范围，通过算例比较表明，径向基函数(RBFs)和运动子网格相结合的混合方法既有很好的变形能力，也有较高的计算效率，值得进一步发展和推广。在介绍了离散几何守恒律(DGCL)概念之后，采用二维几何模型进行分析，指出其机理是离散过程中体积增量与网格面元扫过的体积不相等造成的，把目前国内外应用的算法分为面积修正法、给定速度的面积修正法、速度修正法和体积修正法共4类，对其应用范围和存在的问题进行讨论，认为提出的体积修正算法既可以保证流固界面条件，也可以用于时间多层格式。

非结构网格； 网格变形； 非定常流动； 几何守恒律； 界面耦合

有相对运动边界的非定常流动在自然界很常见，比如飞鸟、游鱼、走兽、以及人体内的血液流动等。这类流场具有相同的特点，即物体的形状、位置随时间变化，固体与流体相互作用，此类动力学系统常称为流固耦合(Fluid-Structure)问题。在航天与航空领域还有一类是流场中有多个物体，它们之间存在相对运动，而且大部分情况下运动还受到流场的影响。例如，外挂物与载机分离、座舱盖/座椅的弹射、多级火箭的级间分离、多弹头再入、子母弹抛撒、爆炸弹片飞散和冲击波驱动物体运动等，需要采用流体方程和六自由度刚体运动方程(Fluid-Rigid)耦合计算，为区别于前一类流固耦合问题，本文称为多体分离问题。

对非定常流动进行数值模拟时，物理空间随边界运动而变化，导致计算中网格也要随时间变化，故需要发展与流场计算过程相关的网格技术。根据计算中流场内网格数目是否变化分为两类算法：一种是网格没有变形、通过增减网格数目实现物理空间变化，目前主要有笛卡儿自适应网格和运动嵌套网格；另一种是保持计算网格数目不变、采用变形动网格技术描述流场物理空间随时间的变化。

嵌套网格又称为重叠网格，采用多块贴体网格处理复杂外形，在物理边界处或网格重叠区内建立人工边界，称为“洞”边界。“洞”内单元是不参与计算的无效网格，“洞”外单元是参与计算的有效网格，“洞”边界和相邻子块之间采用插值公式建立信息传递关系。国内采用嵌套网格计算定常流动的文献较多，最早的应用可以追溯到1991年杨永健和张鲁民研究带有4个助推火箭的复杂流场模拟[1]，阎超等在自动判明边界和快速挖洞等方面有算法的改进，在复杂外形的应用方面也取得实效[2]。近几年国内采用子块在静止背景块上运动的嵌套网格技术模拟包含运动边界的流动[2-5]，由于计算过程中各子网格块存在相对运动，子网格相对位置随时间变化，因此每一个时间步都需要重新确定“洞”边界，并重新判断每一个网格单元是否为有效网格，这对于网格量数百万乃至上千万的应用问题将显著增加计算量，在外形复杂、分块较多情况下，描述子块之间关系时比较繁琐，算法的程序实现也较为困难。

笛卡儿网格(Cartesein Grids)采用四边形(二维)或六面体(三维)形状的网格，并与直角坐标系的坐标轴平行，是一种出现最早的用于计算流体力学(CFD)计算的网格划分方法。笛卡儿网格具有生成简单、流动求解器容易实现等优点，但是难于描述复杂几何外形。为了提高边界附近流场的计算精度，通常采用局部网格加密技术或网格分区技术，在几何形状不规则的壁面附近进行特殊处理，这些边界处理算法会导致数据结构变复杂，降低计算效率，因此笛卡儿网格一直没有成为主流。采用自适应笛卡儿网格可以实现运动边界，但在计算过程中需要建立网格之间的动态数据链表，且每一步计算都需要重新判断边界单元，在网格量较大的情况下，大量繁杂的搜索和插值过程将消耗巨大的计算机资源，甚至会远大于求解流体力学方程本身。目前国内对笛卡儿网格的研究和应用非常少，其中李盾等采用该技术模拟多体分离问题取得很好效果[6-7]。

变形动网格早期主要用于激波装配法模拟定常流场，近20年逐步回归到边界运动问题的计算。本文作者所在课题组从1998年开始从事变形动网格研究，并于2009年出版相关专著[8]，下面将对这一领域的研究历史和最新进展进行综述。提出以上几种网格技术的年代很早，例如，变形动网格在20世纪70年代曾被广泛应用，形成的相关文献非常多，因此本文选择文献时对国外主要采用标志性的，对国内尽可能全面地介绍研究现状。

1　非结构动网格技术

网格生成技术曾是CFD的重要内容，先后出现了结构网格、叠合网格、搭接网格、非结构网格、直角网格、混合网格等提法。按照数据结构是否有序，主要分为结构和非结构两类，非结构网格除了相邻单元编码无序外，也包括控制体形状和面元数目不受限制。严格的说，混合网格是指分块以后有些采用有序编码、有些采用无序编码的算法，现在把非结构网格中出现六面体形状的网格称为“混合网格”的提法不准确。

很多文献按照求解方程类型把网格变形方法分为代数方法和偏微分方程方法两类，本文按照构造思想分为物理比拟、椭圆光顺、插值、运动子网格及其混合这5种方法。网格变形有3个基本要求：变形中不出现失效单元，保持较好品质；能够精确描述边界，即保证网格是贴体的；不能造成CFD求解器效率大幅度降低。下面按照这3条标准来评价这5种方法。

1.1物理比拟方法

这是一类将网格点的运动比拟为某种物理过程的网格变形方法，常用的包括弹簧比拟法和固体比拟法。

1990年Batina首次采用弹簧比拟法实现三角形网格的变形[9]。它的原理是将网格单元的边视为弹簧，整个计算网格构成一个弹簧系统，在弹簧系统内部节点(网格点)建立力的平衡方程组，边界的运动或变形导致弹簧系统受到拉伸或压缩，弹簧节点受力发生变化，通过求解整个弹簧系统节点受力的平衡方程组来确定网格节点新的位置。这种方法只能描述弹簧的拉压变形，扭转变形易导致网格折穿(Snap-Through)现象。1998年Farhat等在二维网格的弹簧节点处通过施加扭转弹簧增加了网格单元的抗扭转能力，并取得良好效果，但在推广到三维网格时遇到了困难[10-11]。2000年Blom根据弹簧边所对应的三角形单元的顶角对线弹簧刚度系数进行修正，提出了半扭转弹簧方法[12]。2003年郭正等针对四面体单元，采用不包含弹簧边的二面角作为顶角，把该方法推广到了三维情形，同时通过求解固体导热方程得到内部节点的温度，并将其作为参数用来增加运动边界附近网格层的弹簧刚度系数，提高了网格变形能力[13]。弹簧方法只适用于三角形网格和四面体网格，应用于其他类型网格则需要剖分重构，例如，六面体单元剖分6个四面体网格[8]，增加了计算量和实施难度，限制了该方法的应用。2005年Bottasso等提出球点弹簧方法，在以网格边构成的弹簧系统内再添加新弹簧，这些新弹簧的起点位于网格节点，终点止于该点在所对面内的垂足，如此一来，格点便为多面球所包围，从而避免折穿，可以用于四边形和六面体单元的网格变形[14-15]。弹簧比拟法所求解的力平衡方程组对角占优，采用Jacobi迭代或Seidel迭代较快收敛，因此得到大量应用，但其变形能力比固体比拟法差。

固体比拟法是Tezduyar等于1992年提出的，它将计算域视为弹性体，将运动边界的位移作为施加在弹性体上的变形载荷，在每个网格节点上建立一组弹性力学基本方程，通过计算该方程得到在上述变形载荷下各个网格节点的位移，从而确定新的网格节点位置[16]。弹性体方法的模型完备，具有比较成熟的计算方法，适用于任何网格类型，通过调整弹性模量、泊松比、添加源项等改进措施，使其具有很强的网格变形能力，至今依然在应用[17-26]。

还有其他的物理比拟方法，如Kennon等提出的流动比拟法[27]和陈炎等提出的温度体比拟法[28-31]，因其缺少普适性，这里不再介绍。

物理比拟方法中，弹性体法需要求解偏微分方程组，计算量大，不适用于大规模问题，弹簧法使用简单，目前应用最为广泛，但是变形能力较差。

1.2网格光顺方法

基于偏微分方程的网格生成算法很早就被广泛应用[32]，1996年Löhner等用于网格变形，通过求解Laplace方程把边界运动逐步传递到计算区域内部网格点，由于椭圆型方程具有在求解域内部不会产生极值的数学特性，这种方法得到的网格变形光滑过渡，因此称为网格光顺方法[33]。计算均匀扩散系数的Laplace方程得到的位移主要和网格点所处位置相关，同样变形相对于不同网格单元的效果不一样，通过调整扩散系数让小单元经历较小变形、大单元经历较大变形，提高网格变形能力[34-38]。近几年探索从双调谐方程和双椭圆方程对网格实施变形[39-40]。由于弹性力学基本方程和Laplace方程的数学性质类似，实际应用也表明网格光顺法和弹性体法相似，具有较强的网格变形能力，但是计算量大，实施较复杂。

1.3插值方法

采用插值函数根据已知边界网格点位移插值得到内部网格点位移，分为显式和隐式两种。沿着网格线根据确定的边界位置，采用代数插值、多项式插值、样条插值等直接计算网格内点位置的显式插值方法，在激波装配法、气动弹性计算中使用几十年了，由于这种简单插值仅适用于结构网格和简单外形，因此很少作为变形网格技术讨论。近几年通过采用基于距离的插值函数建立了适用于复杂外形、任意形状网格的显式插值[41-44]，其中Shepard提出的逆距加权插值(Inverse Distance Weighting Interpolation， IDW)[45],采用关于未知点到已知点距离倒数的函数作为权重，通过已知点集的数据的加权平均得到未知点处的数据，取得很好效果[46-48]。显式插值具有很高的计算效率，适合于大规模的并行计算，但是不考虑连接关系的“点对点”特性使其变形后网格质量很快下降，在外形或边界运动等情况下，其效果远不如考虑相邻点影响的隐式插值。常用的隐式插值是径向基函数(Radial Basis Functions， RBFs)法，采用点与点之间径向距离的函数，在已知运动边界离散点数据条件下，通过求解线性方程组得到插值函数的系数，然后得到内部网格点位置。该算法数据结构简单，可以应用于任何类型网格，并且有完备的理论基础[49]。2007年Boer等用于网格变形，发现计算插值系数需要的线性方程组规模是边界点数目的平方，对于三维问题计算量很大[50]，后来对这种方法进行改进减少了计算量，但算法变得较为复杂[51-54]。

尽管插值方法很少发生变形失败，但是主要考虑距离信息的特性使其难以保证网格质量，RBFs涉及到矩阵求逆，网格规模较大后计算效率也值得考虑。黏性流动计算时采用长宽比较大的四边形或六面体网格来分辨边界层，常规的变形算法难以满足要求，插值方法具有明显的优势。

1.4运动子网格方法

运动子网格法早期特指Delaunay图映射方法，是Liu等在2006年提出的一种动网格方法[55]，在所有动边界网格点和若干控制点基础上生成Delaunay图，也就是子网格，计算网格包含在子网格内部，每个计算网格点必然属于子网格中的一个单元，可以在子网格单元内部得到计算网格点的相对位置坐标，即得到计算网格节点和子网格单元的映射关系，边界运动牵引子网格运动，利用映射关系便可以得出计算网格节点在变形后的坐标。Delaunay图映射方法具有很高的计算效率，但对于复杂外形和大幅度运动，网格质量下降很快，重新生成需要花费时间。近年来，部分学者提出一些改进算法，肖天航等提出了双重Delaunay图动网格生成算法[56]，在一定程度上增强动网格的质量和变形的鲁棒性，周璇等采用Delaunay图映射方法计算运动子网格点相对于动边界的相对位置，比较方便地实现了对弹簧近似方法的逐层边界修正，利用弹簧比拟法计算运动子网格的变形[57]，可以用于黏性计算。这种背景网格变形牵引内部网格运动的思路，也不仅仅局限于Delaunay图，例如，Lefrançois采用的运动子网格包含了计算域内的点[58]，且运动子网格可以根据不同的问题进行调整，比Delaunay图要灵活，因此，采用运动子网格方法表述这类方法比Delaunay图映射方法更合适。

运动子网格方法的优点是计算效率高，缺点是用于复杂构型生成背景网格需要经验，大幅度运动特别是大角度转动易出现背景网格交叉引起的变形失败，重新生成背景网格常需要人工干预。

1.5变拓扑方法

以上列举的网格变形方法，网格点之间的连接关系不改变，在动边界经历大位移和大变形时，网格质量必然会变差，如果放弃网格点之间连接关系不变的限制，则动网格的变形能力会进一步增强。2011年Alauzet和Olivier用弹性体比拟法模拟叶片旋转，允许改变网格节点间的连接关系，极大增强了变形能力，实现了二维叶片的360° 旋转[59-60]，Isola等采用对质量差的网格单元进行边交换也具有同样效果[61-62]。2013年Wang和Perssony用弹簧比拟法进行二维网格变形，通过改变网格节点间的连接关系模拟了双翼型扑动流场[63]。

连接关系确定后计算量很少，变拓扑方法的计算效率最高，但是数据结构变化较频繁，需要求解器进行改造，实现较为复杂，目前应用范围较窄。

1.6混合方法

混合方法是指同时采用两种以上方法的组合对网格进行变形。最早用于多块网格求解复杂外形[64]，用弹簧比拟法计算多块结构网格的块顶点位移，然后用超限插值方法更新块内网格节点坐标。Zhou和Li通过多种方法的组合，得到了一种混合网格变形方法[65]。

本文作者注意到这种方法的优势在于兼顾计算效率和网格形状适应性，沿着这一思路把径向基函数方法作为计算网格，比较了弹簧法和运动子网格方法作为变形控制背景网格，发现后者具有变形能力强、计算效率高的优点，提出RBFs-MSA网格变形算法[66]，下面通过具体算例进行介绍。

2　RBFs-MSA网格变形算法

RBFs-MSA也属于混合方法，在生成如图1所示的计算网格时，还需要生成背景网格，见图2。可以看出，这种混合方法综合了其他算法的优势，计算网格几何形状任意，有效满足黏性流动模拟需要的异向加密需求，背景网格为三角形(二维)或四面体(三维)，具有强的变形能力。流场计算过程中，两套网格按照如下程序组合使用：

1) 在计算网格基础上通过网格细化或者重新生成的方法得到子网格，子网格边界点和内点根据具体问题自由控制，但是数目远少于计算网格。

2) 计算网格内点在运动子网格单元中的相对面积或体积坐标(映射关系)。

3) 计算动边界的位移，更新计算网格边界点坐标，这些点中包含子网格的边界点。

4) 利用径向基函数插值得到运动子网格内点的坐标。

5) 利用映射关系得到计算网格内点坐标。

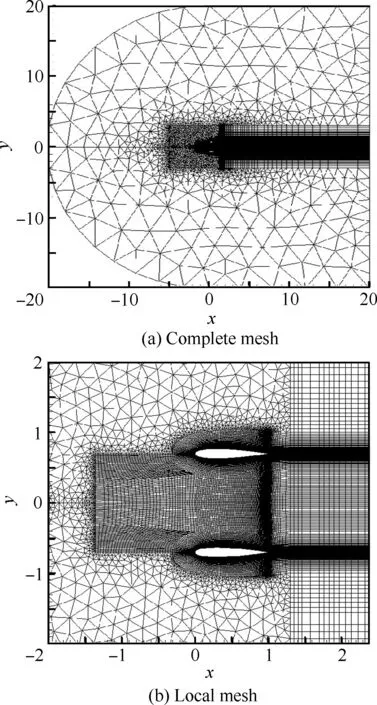
图1　计算网格Fig.1　Computational mesh

图2　背景网格Fig.2　Background mesh

国外常用来检验网格变形算法的经典算例是Anderson等完成的扑翼实验[67]。弦长记为c,其上下沉浮运动和俯仰运动规律分别为

(1)式中：h和h0分别为沉浮运动的位移和振幅；ω为振动频率；t为时间；φh和φθ分别为沉浮和俯仰运动的相位角；θ和θ0分别为俯仰角和俯仰运动的振幅。

对于周期运动，更关心的是沉浮和俯仰运动的相位角φh和φθ的差：ψ=φθ-φh=75°。在实验中采用机械结构实现组合运动的振动频率ω需要根据机构运动特性计算，Anderson引入最大名义迎角α0=15°和后缘点最大位移At定义的斯特劳哈数St=ωAt/(2πu)，u为参考速度，对应的减缩频率k=0.5ωc/u。在给定振幅h0=0.75c和St以后，结合减缩频率公式、斯特劳哈数定义公式以及名义迎角定义公式，可计算沉浮和俯仰组合运动过程中角振幅θ0和振动频率ω：

α0=arctan(2kh0)-θ0

(2)

计算区域以翼型前缘点为圆心，半径为15c的半圆后面连接长度为15c的矩形。计算网格采用C形贴体网格，总共有25 200个四边形网格，翼型表面网格上分布有270个节点，在翼型附近采用逐层加密，距物面第一层网格单元的高度为0.000 02c，并在前后缘进行适当加密。背景网格含有408个三角形单元，224个节点，其中翼型边界节点为21个。

本文比较了背景网格整体刚性运动、背景网格采用RBFs和两套网格RBFs-MSA这3种网格运动方法计算十步所需的CPU时间，分别为40 s、341 s和56 s。第一种方法采用直接解析表达式，因此计算网格更新所用时间相比于计算流动方程的时间几乎可忽略，由此可见RBFs-MSA方法可以比RBFs大量减少计算时间。

本文分别进行层流和湍流的模拟，湍流模式选择Spalart-Allmaras (S-A)模型和Wilcox的k-ω模型，图3是平均推力系数CT和平均输入功率系数CP与实验的比较。本文计算的推力系数与Shyy[68]和Young[69]的计算结果符合较好，所有计算值略低于实验值。在St<0.3范围内，本文计算的平均输入功率系数与文献符合较好，当St>0.4时，计算结果比文献偏大。

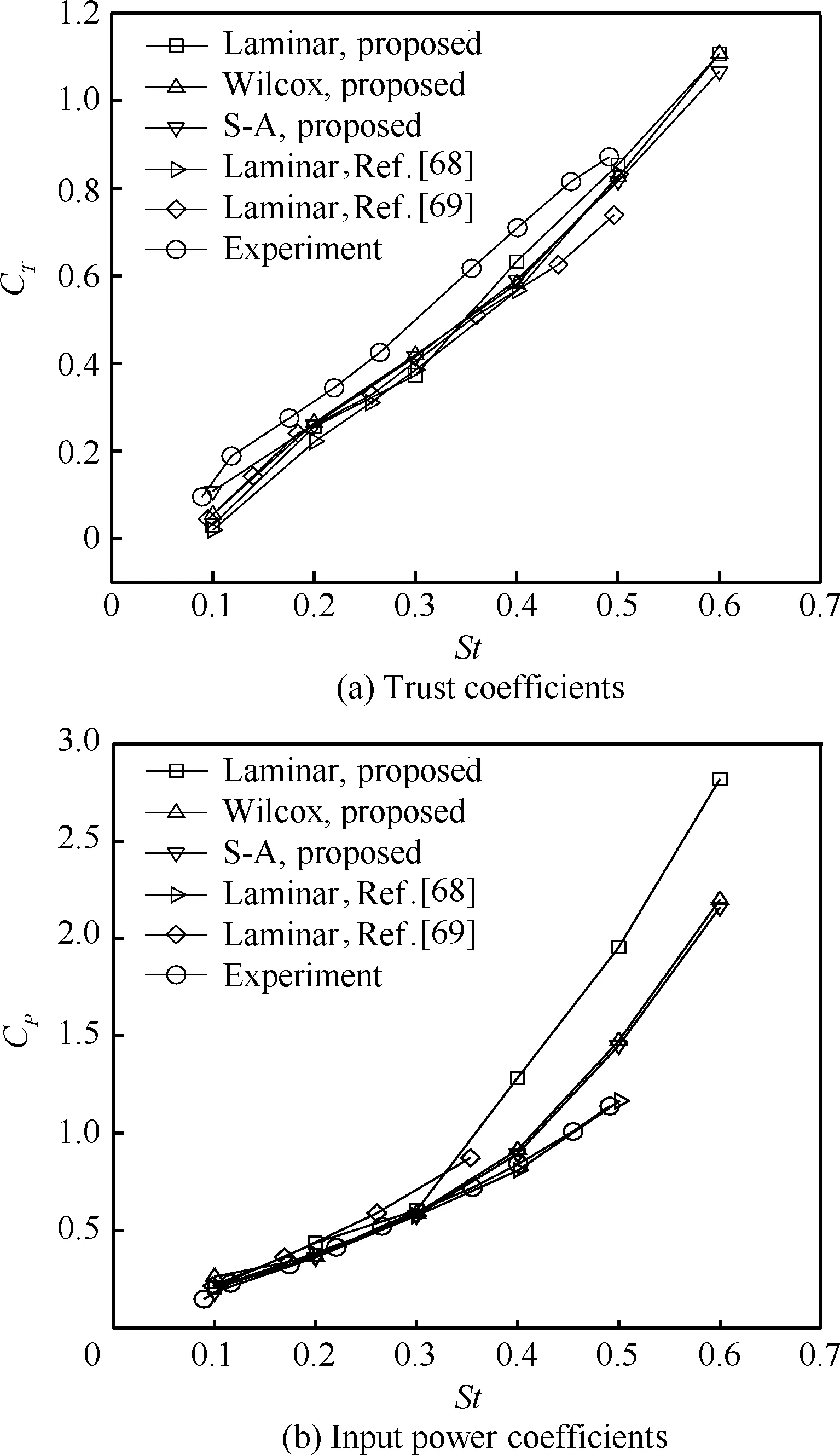
图3　平均推力系数和平均输入功率系数比较Fig.3　Comparison between average thrust coefficients and average input power coefficients

3　离散几何守恒律

变形网格技术常采用基于任意拉格朗日-欧拉(Arbitrary Lagrangian-Eulerian， ALE)方程描述的有限体积法。对于三维非定常可压缩Navier-Stokes方程为

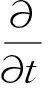
(3)

式中：Ω为控制体；∂Ω为控制边界；Q为守恒量；Fc为对流通量；Fv为黏性通量；dV为体积微元；dS为面积微元；n为控制体边界外法向向量；xc为网格运动速度。由于xc是时间和空间的函数，在离散以后可能会引入新的误差，即使对于均匀流场也难保证式(3)严格成立，为此，需要考虑几何守恒律(GeometricConservationLaw，GCL)。

几何守恒律概念最早于1978年在AIAA会议上由Thomas和Lombard提出[70-71]，当时主要讨论有限差分法，也提及ALE有限体积法，给出的几何守恒律方程为

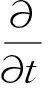
(4)

(5)

文献[8]中证明以上网格的几何不等引起流场误差可以达到O(1)量级，因此，不满足DGCL对ALE方程的有限体积法计算会产生很大影响。由于DGCL与求解流场的时空离散格式相关，国外文献构造了很多种几何守恒律算法，选择的修正参数不同，本文作者把国外的算法分为3类：面积修正法(包含给定速度的面积修正法)、速度修正法和体积修正法。

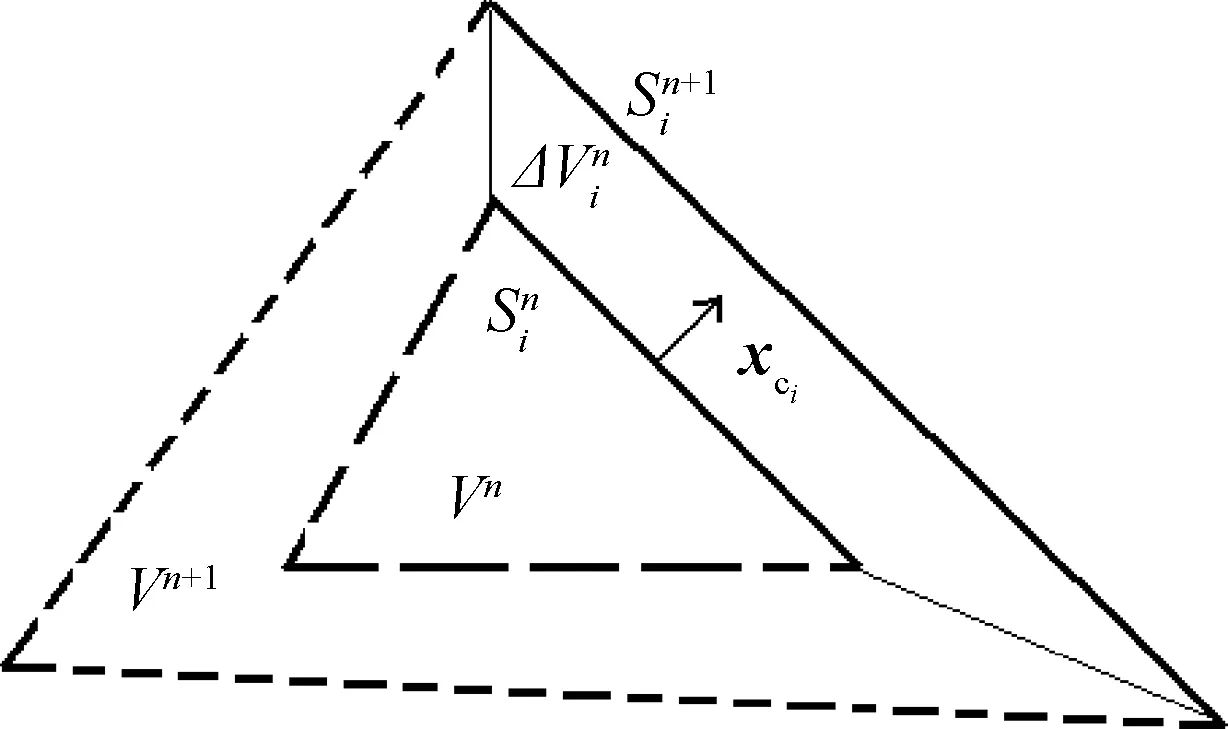
图4　离散几何守恒律示意图Fig.4　Schematic diagram of discrete geometricconservation law

3.1面积修正法

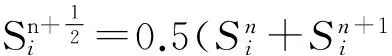
3.2给定速度的面积修正法

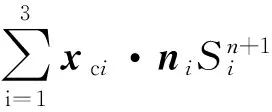
(6)

为满足DGCL要求，Guillard和Farhat提出了两种实现方法[72]：一种是在tn和tn+1时刻之间构造多套网格，假设网格按照已知规律运动和变形，在这些网格上分别计算通量，然后对这些通量进行加权平均；另一种是在构造的多套网格中得到一个平均网格，然后在这个平均网格构型上计算通量。为了保证式(4)的离散格式具有时间二阶精度，需要涉及20个参数来构造多个时间层的网格运动速度和中间面积[73-74]。这类算法推导过程复杂，增加了计算量，另外，通量计算时所用的流场变量都是tn+1时刻的流场变量，这样处理至少在物理意义上是不明确的，国内还没有看到具体应用。

3.3速度修正法

Mavriplis和Yang发现按照Guillard和Farhat方法确定的参数不惟一，针对BDF2格式，有些情况下并不都严格满足DGCL条件，于是提出采用根据DGCL条件计算出来的速度ug来代替实际的网格运动速度xc的修正速度算法[75]，即

(7)

Mavriplis和Yang的方法不需要引入中间网格，计算通量时网格位置与流场变量在时间上是一致的，消除了Guillard和Farhat方法中物理量与网格在时间上的不匹配。但是ug≠xc又会引起3.4节讨论的流固耦合界面算法的精度问题。

Hyung和Yannis[76]曾提出通过在控制方程右端引入源项的方式来消除DGCL误差，虽然出发点有所不同，但最终落脚点还是在于修正网格运动速度。

值得指出的是张来平等也提出过类似的思想来处理一阶Euler后差格式的DGCL算法[77]，先用面积修正法计算平均面积，然后采用式(8)计算网格速度，即

(8)

尽管不满足DGCL会给流场计算引入误差，文献[78]的数值试验表明误差可以达到O(1)量级，但是误差变化规律还缺乏理论研究，有些格式表现为周期振荡、有些格式表现为单调增加，由此引出的DGCL和ALE格式稳定性之间的关系是目前学术界主要争论的问题。Farhat和Geuzaine[74]认为满足DGCL是ALE格式具有和静止网格格式相同稳定性的充分必要条件，Boffi和Gastaldi[79]给出了相反的结论，Masud[80]在满足DGCL的前提下，对网格速度对稳定性和收敛性的影响进行了研究，认为网格运动速度能够影响稳定的时间步长，且计算误差与网格相对运动速度有关。

3.4体积修正法

上述3种修正算法均采用修正右端项的思路来解决问题，本文提出完全不同的新思路，即对于以上BDF2格式，按照不同的时间层，有3种修正方法：

1) 修正tn+1时间层的体积Vn+1，计算时用体积V′代替进行计算，即

(9)

2) 修正tn时间层的体积Vn，计算时用V″代替，即

(10)

3) 修正tn-1时间层的体积Vn-1，计算时用V‴代替，即

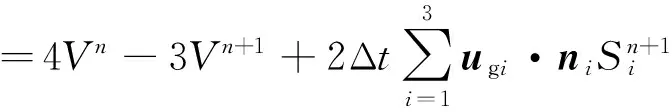
(11)

在非定常计算中，采用上述不同的修正方法都能在一定程度上消除DGCL误差，但在不同的计算问题中，实际效果存在一定差异。张来平等从截断误差的观点出发，曾对均匀流和等熵涡问题采用不同的修正方法进行过测试、分析[81]。

本文构建了如下两个模型来验证DGCL算法。计算中离散几何守恒律分别采用Mavriplis算法[75]、张来平算法[77]和本文提出的3种算法，除了张来平算法采用一阶Euler后差格式，其余采用BDF2格式，CFL数都取为200。

第1个模型是在x∈[-2,2]和y∈[0,1]构成的矩形内充满均匀密度ρ=1、压力p=1/γ的静止气体(以气体声速作为速度无量纲参数)，计算中采用左右两条边上网格点静止，初始时刻上下两条边上中点处的网格点在水平方向正弦运动，从而带动整个流场的网格运动和变形。计算中焓的绝对误差随无量纲时间t的变化如图5(a)

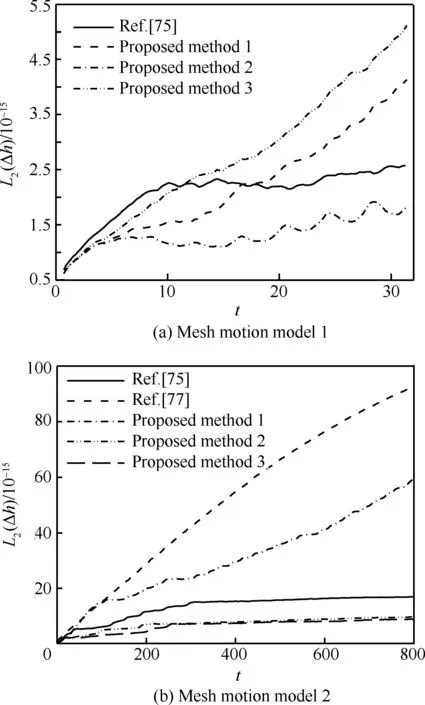
图5　计算误差Fig.5　Calculation errors

所示，其中横坐标为无量纲时间，纵坐标为全场焓值绝对误差的2-范数，误差为10-15量级，接近计算机随机误差。

第2个模型考核网格形状的影响，取x∈[0,1]和y∈[0,1]构成的正方形计算域，结点为51×51的四边形网格，保持边界点不动，内点按照如下规律运动：

(12)

式中：(x0,y0)和Δx=Δy=0.02是网格的初始位置和间距。从焓的绝对误差随无量纲时间变化(如图5(b)所示)看出，误差也接近计算机随机误差。

需要指出的是体积修正法对非均匀流场存在守恒性问题，理论上只能用于空间二阶精度的有限体积法。

4　界面耦合算法

从图5(a)来看，本文的体积修正法和速度修正法没有本质差别，但是考虑到流固耦合问题或多体分离问题的边界是运动的，那么速度修正法不能保证界面耦合条件的精度。下面对此进行讨论。采用时间相关法求解流体力学方程本质上是时间变量的一次积分计算，界面上流体速度记为vf，CFD在离散空间上构建，这决定了从t推进到t+Δt过程中速度保持为常数，因此，边界位置更新为

(13)

式中：rf为界面上的流体位移。

固体运动学方程本质是时间变量的二次积分，以刚体动力学方程mrtt=Fair为例来说明(m为物体质量，rtt为物体位移对时间的二阶导数，即加速度，Fair为物体气动力的合力)，从t推进到t+Δt过程中加速度保持为常数，采用最简单的式(14)可以看出速度是变化的。

(14)

式中：vs为界面上的固体运动速度；rs为界面上的固体运动位移；m为质量；Fair为气动力。

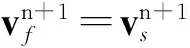
如果DGCL采用面积修正算法，与网格运动速度无关，以上满足位置相等条件。如果采用假设运动规律的面积修正算法，可以在二阶精度条件下实现位置相等[74]。如果采用速度修正法计算，网格运动速度ug既不能保证等于流体界面速度vf，也不等于刚体运动速度vs，更无法满足位置相等条件，因此，这类算法在流场和结构之间信息交换过程中必然引入误差。本文提出的体积修正算法与网格运动速度和面积变形均无关，使得DGCL算法与流固界面信息传递算法不再相关，可实现严格满足位置或速度条件的要求。

5　结　论

1) 径向基函数和运动子网格相结合的混合方法既有很好的变形能力，也有较高的计算效率，值得进一步发展和推广。

2) 需要满足离散几何守恒律的本质原因是离散过程中体积增量与网格面元扫过的体积不相等。

3) 体积修正算法既可以保证流固界面条件，也可以用于时间多层格式，具有良好的应用前景。

[1]杨永健, 张鲁民. 应用重叠网格技术求解复杂组合体无粘流场[J]. 空气动力学报, 1991, 31(1): 51-57.

YANG Y J, ZHAMG L M. Numerical simulation of inviscid flow over a complicated body using an overlapping grid technique[J]. Acta Aerodynamica Sinica, 1991, 31(1): 51-57 (in Chinese).

[2]范晶晶, 阎超, 张辉. 重叠网格洞面优化技术的改进与应用[J]. 航空学报, 2010, 31(6): 1127-1133.

FAN J J, YAN C, ZHANG H. Improvement of hole-surface optimization technique in overset grids and Its application[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(6): 1127-1133 (in Chinese).

[3]张培红, 王明, 邓有奇, 等. 武器分离及舱门开启过程数值模拟研究[J]. 空气动力学学报, 2013, 31(3): 277-281.

ZHANG P H, WANG M, DENG Y Q, et al. Numerical simulation of store separation and door operation[J]. Acta Aerodynamica Sinica, 2013, 31(3): 277-281 (in Chinese).

[4]肖中云, 江雄, 牟斌, 等. 并行环境下外挂物动态分离过程的数值模拟[J]. 航空学报, 2010, 31(8): 1509-1516.

XIAO Z Y, JIANG X, MOU B, et al. Numerical simulation of dynamic process of store separation in parallel environment[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(8): 1509-1516 (in Chinese).

[5]刘学强, 伍贻兆, 夏健. 多重网格法在非结构网格中的应用[J]. 计算物理, 2002, 19(4): 357-361.

LIU X Q, WU Z Y, XIA J. Application of the multigrid method in unstructured meshes[J]. Chinese Journal of Computational Phyfics, 2002, 19(4): 357-361 (in Chinese).

[6]李盾, 何跃龙, 纪楚群. 多体分离数值模拟研究与应用[C]//北京力学会第19届学术年会论文集. 北京： 北京力学会, 2013: 121-122.

LI D, HE Y L, JI C Q. Numerical simulation research and application of multi-body separation[C]//The Beijing Society of Theoretical and Applied Mechanics 19th Annual Conference Proceedings. Beijing: The Beijing Society of Theoretical and Applied Mechanics, 2013: 121-122 (in Chinese).

[7]何跃龙, 李盾, 刘晓文. 非结构直角网格动网格方法[C]//北京力学会第18届学术年会论文集. 北京： 北京力学会, 2012: 19-20.

HE Y L, LI D, LIU X W. Dynamic unstructured cartesian grid method[C]//The Beijing Society of Theoretical and Applied Mechanics 18th Annual Conference Proceedings. Beijing: The Beijing Society of Theoretical and Applied Mechanics, 2012: 19-20 (in Chinese).

[8]刘君, 白晓征, 郭正. 非结构动网格计算方法-及其在包含运动界面的流场模拟中的应用[M]. 长沙: 国防科技大学出版社, 2009.

LIU J, BAI X Z, GUO Z. Dynamic unstructured grid method and its application in simulation of unsteady flows involving moving boundaries[M]. Changsha: National University of Defense Technology Press, 2009 (in Chinese).

[9]BATINA J T. Unsteady euler airfoil solutions using unstructured dynamic meshes[J]. AIAA Journal, 1990, 28(8): 1381-1388.

[10]FARHAT C, DEGAND C, KOOBUS B, et al. Torsional springs for two-dimensional dynamic unstructured fluid meshes[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 163(1): 231-245.

[11]DEGAND C, FARHAT C. A three-dimensional torsional spring analogy method for unstructured dynamic meshes[J]. Computers & Structures, 2002, 80(3): 305-316.

[12]BLOM F J. Considerations on the spring analogy[J]. International Journal for Numerical Methods in Fluids, 2000, 32(6): 647-668.

[13]郭正, 刘君, 瞿章华. 非结构动网格在三维可动边界问题中的应用[J]. 力学学报, 2003, 35(2): 140-146.

GUO Z, LIU J, QU Z H. Dynamic unstructured grid method with applications to 3D unsteady flows involving moving boundaries[J]. Acta Mechanica Sinica, 2003, 35(2): 140-146 (in Chinese).

[14]BOTTASSO C L, DETOMI D, SERRA R. The ball-vertex method: A new simple spring analogy method for unstructured dynamic meshes[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(39): 4244-4264.

[15]ACIKGOZ N, BOTTASSO C L. A unified approach to the deformation of simplicial and non-simplicial meshes in two and three dimensions with guaranteed validity[J]. Computers & Structures, 2007, 85(11): 944-954.

[16]TEZDIUAR T E, BEHR M, MITTAL S, et al. Computation of unsteady incompressible flows with the finite element methods: Space-time formulations, iterative strategies and massively parallel implementations[J]. Asme Pressure Vessels Piping Div Publ PVP, 1992, 246(1): 7-24.

[17]JOHNSON A A, TEZDUYAR T. Mesh update strategies in parallel finite element computations of flow problems with moving boundaries and interfaces[J]. Computer Methods in Applied Mechanics and Engineering, 1994, 119(1-2): 73-94.

[18]JOHNSON A A, TEZDUYAR T E. Advanced mesh generation and update methods for 3D flow simulations[J]. Computational Mechanics, 1999, 23(2): 130-143.

[19]STEIN K, TEZDUYAR T, BENNEY R. Mesh moving techniques for fluid-structure interactions with large displacements[J]. Journal of Applied Mechanics, 2003, 70(1): 58-63.

[20]STEIN K, TEZDUYAR T E, BENNEY R. Automatic mesh update with the solid-extension mesh moving technique[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(21): 2019-2032.

[21]CHIANDUSSI G, BUGEDA G, ONATE E. A simple method for automatic update of finite element meshes[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 16(1): 1-19.

[22]XU Z, ACCORSI M. Finite element mesh update methods for &uid-structure interaction simulations[J]. Finite Elements in Analysis and Design, 2004, 40(9): 1259-1269.

[23]SMITH R W. A PDE-based mesh update method for moving and deforming high reynolds number meshes: AIAA-2011-0472[R]. Reston: AIAA, 2011.

[24]SMITH R W, WRIGHT J A. A Classical elasticity-based mesh update method for moving and deforming meshes: AIAA-2010-0164[R]. Reston: AIAA, 2010.

[25]YANG Z, MAVRIPLIS D J. Unstructured dynamic meshes with higher-order time integration schemes for the unsteady Navier-Stokes equations: AIAA-2005-1222[R]. Reston: AIAA, 2005.

[26]KARMAN S L, ANDERSON W K, SAHASRABUDHE M. Mesh generation using unstructured computational meshes and elliptic partial differential equation smoothing[J]. AIAA Journal, 2006, 44(6): 1277-1286.

[27]KENNON S R, MEYERING J M, BERRY C W. Geometry based Delaunay tetrahedralization and mesh movement strategies for multi-body CFD: AIAA-1992-4575[R]. Reston: AIAA, 1992.

[28]陈炎, 曹树良, 梁开洪, 等. 基于温度体模型的动网格生成方法及在流固耦合振动中的应用[J]. 振动与冲击, 2010, 29(4): 1-5.

CHEN Y, CAO S L, LIANG K H, et al. A new dynamic grids based on temperature analogy and its application in vibration engineering with fluid-solid interaction[J]. Journal of Vibration and Shock, 2010, 29(4): 1-5 (in Chinese).

[29]陈炎, 曹树良, 梁开洪, 等. 温度体动网格模型中控制参数的研究[J]. 计算物理, 2010, 27(3): 396-402.

CHEN Y, CAO S L, LIANG K H, et al. Parameter control in temperature analogy method[J]. Chinese Journal of Computational Phyfics, 2010, 27(3): 396-402 (in Chinese).

[30]陈炎, 张勤昭, 曹树良. 温度体动网格方法的旋转变形能力[J]. 排灌机械工程学报, 2012, 30(4): 447-451.

CHEN Y, ZHANG Q Z, CAO S L. Rotational deformability of temperature analogy method[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 30(4): 447-451 (in Chinese).

[31]陈炎, 张勤昭, 曹树良, 等. 基准温度分布动网格生成方法的研究及应用[J]. 北京理工大学学报, 2012, 32(9): 900-904.

CHEN Y, ZHANG Q Z, CAO S L, et al. A new method of dynamic grid generation based on reference temperature distribution[J]. Transactions of Beijing Institute of Technology, 2012, 32(9): 900-904 (in Chinese).

[32]THOMPSON J F, WARSI Z U A, MASTIN C W. Numerical grid generation: Foundations and applications[M]. Amsterdam: North-holland, 1985.

[33]LÖHNER R, YANG C. Improved ALE mesh velocities for moving bodies[J]. Communications in Numerical Methods in Engineering, 1996, 12(10): 599-608.

[34]LOMTEV I, KIRBY R M, KARNIADAKIS G E. A discontinuous Galerkin ALE method for compressible viscous flows in moving domains[J]. Journal of Computational Physics, 1999, 155(1): 128-159.

[35]CALDERER R, MASUD A. A multiscale stabilized ALE formulation for incompressible flows with moving boundaries[J]. Computational Mechanics, 2010, 46(1): 185-197.

[36]HUSSAIN M, ABID M, AHMAD M, et al. A parallel implementation of ALE moving mesh technique for FSI problems using openMP[J]. International Journal of Parallel Programming, 2011, 39(6): 717-745.

[37]MASUD A, BHANABHAGVANWALA M, KHURRAM R A. An adaptive mesh rezoning scheme for moving boundary flows and fluid-structure interaction[J]. Computers & Fluids, 2007, 36(1): 77-91.

[38]MASUD A, HUGHESB T J R. A space-time Galerkin/least-squares finite element formulation of the Navier-Stokes equations for moving domain problems[J]. Computer Methods in Applied Mechanics and Engineering, 1997, 146(1): 91-126.

[39]HELENBROOK B T. Mesh deformation using the biharmonic operator[J]. International Journal for Numerical Methods in Engineering, 2003, 56(7): 1007-1021.

[40]WANG Q, HU R. Adjoint-based optimal variable stiffness mesh deformation strategy based on bi-elliptics equations[J]. International Journal for Numerical Methods in Engineering, 2012, 90(5): 659-670.

[41]YIGIT S, FER M S, HECK M. Grid movement techniques and their influence on laminar fluid-structure interaction computations[J]. Journal of Fluids and Structures, 2008, 24(6): 819-832.

[42]ALLEN C B. Parallel flow-solver and mesh motion scheme for forward flight rotor simulation: AIAA-2006-3476 [R]. Reston: AIAA, 2006.

[43]LIEFVENDAHL M, TRÖENG C. Deformation and regeneration of the computational grid for CFD with moving boundaries： AIAA-2005-1090[R]. Reston: AIAA, 2005.

[44]PERSSON P O, BONET J, PERAIRE J. Discontinuous Galerkin solution of the Navier-Stokes equations on deformable domains[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(17): 1585-1595.

[45]SHEPARD D. A two-dimensional interpolation function for irregularly-spaced data [C]//Proceedings of the 1968 23rd ACM National Conference. New York: ACM, 1968: 517-524.

[46]WITTEVEEN J A S. Explicit and robust inverse distance weighting mesh deformation for CFD： AIAA-2010-0165 [R]. Reston: AIAA, 2010.

[47]WITTEVEEN J A S, BIJL H. Explicit mesh deformation using inverse distance weighting interpolation: AIAA-2009-3936[R]. Reston: AIAA, 2009.

[48]LUKE E, COLLINS E, BLADES E. A fast mesh deformation method using explicit interpolation[J]. Journal of Computational Physics, 2012, 231(2): 586-601.

[49]BUHMANN M. Radial basis functions[M]. Cambridge: Cambridge University Press, 2005.

[50]BOER A D, SCHOOT M S V D, BIJL H. Mesh deformation based on radial basis function interpolation[J]. Computers & Structures, 2007, 85(11): 784-795.

[51]RENDALL T C S, ALLEN C B. Efficient mesh motion using radial basis functions with data reduction algorithms[J]. Journal of Computational Physics, 2009, 228(17): 6231-6249.

[52]RENDALL T C S, ALLEN C B. Reduced surface point selection options for efficient mesh deformation using radial basis functions[J]. Journal of Computational Physics, 2010, 229(8): 2810-2820.

[53]SHENG C, ALLEN C B. Efficient mesh deformation using radial basis functions on unstructured meshes[J]. AIAA Journal, 2013, 51(3): 707-720.

[54]BOS F M, OUDHEUSDEN B W, BIJL H. Radial basis function based mesh deformation applied to simulation of flow around flapping wings[J]. Computers & Fluids, 2013, 79(6): 167-177.

[55]LIU X, QIN N, XIA H. Fast dynamic grid deformation based on Delaunay graph mapping[J]. Journal of Computational Physics, 2006, 211(2): 405-423.

[56]肖天航, 昂海松, 仝超. 大幅运动复杂构型扑翼动态网格生成的一种新方法[J]. 航空学报, 2008, 29(1): 41-48.

XIAO T H, ANG H S, TONG C. A new dynamic mesh generation method for large movements of flapping-wings with complex geometries[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(1): 41-48 (in Chinese).

[57]周璇, 李水乡, 陈斌. 非结构动网格生成的弹簧-插值联合方法[J]. 航空学报, 2010, 31(7): 1389-1395.

ZHOU X, LI S X, CHEN B. Spring-interpolation approach for generating unstructured dynamic meshes[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(7): 1389-1395 (in Chinese).

[58]LEFRANÇOIS E. A simple mesh defomation technique for fluid-structure interaction based on a submesh approach[J]. International Journal for Numerical Methods in Engineering, 2008, 75(9): 1085-1101.

[59]ALAUZET F D R. A changing-topology moving mesh technique for large displacements[J]. Engineering with Computers, 2014, 30(2): 175-200.

[60]OLIVIER G, ALAUZET F. A new changing-topology ALE scheme for moving mesh unsteady simulations: AIAA-2011-0474[R]. Reston: AIAA, 2011.

[61]GUARDONE A, ISOLA D, QUARANTA G. Arbitrary lagrangian eulerian formulation for two-dimensional flows using dynamic meshes with edge swapping[J]. Journal of Computational Physics, 2011, 230(20): 7706-7722.

[62]ISOLA D. An interpolation-free two-dimensional conservative ALE scheme over adaptive unstructured grids for rotorcraft aerocraft aerodynamics[D]. Milano: Politecnico Di Milano, 2012.

[63]WANG L, PERSSONY P O. A discontinuous galerkin method for the Navier-Stokes equations on deforming domains using unstructured moving space-time meshes: AIAA-2013-2833[R]. Reston: AIAA, 2013.

[64]GOPALAKRISHNAN P, TAFTI D K. A parallel multiblock boundary fitted dynamic mesh solver for simulating flows with complex boundary movement: AIAA-2008-4142[R]. Reston: AIAA, 2008.

[65]ZHOU X, LI S. A new mesh deformation method based on disk relaxation algorithm with pre-displacement and post-smoothing[J]. Journal of Computational Physics, 2013, 235(2): 199-215.

[66]LIU Y, GUO Z, LIU J. RBFs-MSA hybrid method for mesh deformation[J]. Chinese Journal of Aeronautics, 2012, 25(4): 500-507.

[67]ANDERSON J M, STREITLIEN K, BARRETT D S, et al. Oscillating foils of high propulsive efficiency[J]. Journal of Fluid Mechanics, 1998, 360(1): 41-72.

[68]LIAN Y, SHYY W. Aerodynamics of low reynolds number plunging airfoil under gusty environment: AIAA-2007-0071[R]. Reston: AIAA, 2007.

[69]YOUNG J. Numerical simulation of the unsteady aerodynamics of flapping airfoils[D]. Canberra: University of New South Wales, 2005.

[70]THOMAS P D, LOMBARD C K. The geometric conservation law-a link beween finite-difference and finite-volume methods of flow computation on moving grids: AIAA-1978-1208[R]. Reston: AIAA, 1978.

[71]THOMAS P D, LOMBARD C K. Geometric conservation law and its application to flow computations on moving grids[J]. AIAA Journal, 1979, 17(10): 1030-1037.

[72]GUILLARD H, FARHAT C. On the significance of the geometric conservation law for flow computations on moving meshes[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 190(11): 1467-1482.

[73]GEUZAINE P, GRANDMONT C, FARHAT C. Design and analysis of ALE schemes with provable second-order time-accuracy for inviscid and viscous flow simulations[J]. Journal of Computational Physics, 2003, 191(1): 206-227.

[74]FARHAT C, GEUZAINE P. Design and analysis of robust ALE time-integrators for the solution of unsteady flow problems on moving grids[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(39): 4073-4095.

[75]MAVRIPLIS D J, YANG Z. Construction of the discrete geometric conservation law for high-order time-accurate simulations on dynamic meshes[J]. Journal of Computational Physics, 2006, 213(2): 557-573.

[76]HYUNG T A, YANNIS K. Strong coupled flow/structure interaction with a geometrically conservative ALE scheme on general hybrid meshes[J]. Journal of Computational Physics, 2006, 219(2): 671-696.

[77]ZHANG L P, WANG Z J. A block LU-SGS implicit dual time-stepping algorithm for hybrid dynamic meshes[J]. Computers & Fluids, 2004, 33(7): 891-916.

[78]KAMAKOTI R, SHYY W. Evaluation of geometric conservation law using pressure-based fluid solver and moving grid technique[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2004, 14(7): 851-865.

[79]BOFFI D, GASTALDI L. Stability and geometric conservation laws for ALE formulations[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(42): 4717-4739.

[80]MASUD A. Effects of mesh motion on the stability and convergence of ALE based formulations for moving boundary flows[J]. Computational Mechanics, 2006, 38(4-5): 430-439.

[81]CHANG X H, MA R, ZHANG L P, et al. Further study on the geometric conservation law for finite volume method on dynamic unstructured mesh[J]. Computers & Fluids, 2015, 120: 98-110.

[82]安效民, 徐敏, 陈士橹. 二阶时间精度的CFD/CSD耦合算法研究[J]. 空气动力学学报, 2009, 27(5): 547-552.

AN X M, XU M, CHEN S L. Analysis for second order time accurate CFD/CSD coupled algorithms[J]. Acta Aerodynamica Sinica, 2009, 27(5): 547-552 (in Chinese).

刘君男， 博士， 教授， 博士生导师。主要研究方向： 空气动力学。

Tel: 0411-84707176

E-mail: liujun65@dlut.edu.cn

刘瑜男， 博士， 讲师。主要研究方向： 燃烧数值模拟。

E-mail: liuyu@nudt.edu.cn

陈泽栋男， 博士研究生。主要研究方向： 计算流体力学， 空气动力学。

E-mail: chenzd_dut@163.com

Unstructured deforming mesh and discrete geometricconservation law

LIU Jun1,*, LIU Yu2, CHEN Zedong3

1. School of Aeronautics and Astronautics, Dalian University of Technology, Dalian116024, China 2. Department of Space Equipment, Academy of Equipment, Beijing101416, China 3. Department of Engineering Mechanics, Dalian University of Technology, Dalian116024, China

A popular method for simulating unsteady flow of fluid-structure interaction or multi-body separation is finite volume method based on arbitrary Lagrangian-Eulerian (ALE) equations, which involves mesh deformation and discrete geometric conservation law. The fundamental principle, state of the art and boundaries of validity of mesh deformation are reviewed following 5 categories of constructing ideas, e.g., physics analogy, ellipse smoothing, interpolation, moving submesh approach (MSA) and hybrid method. A hybrid method which combines the benefits of MSA and radial basis functions (RBFs) interpolation is proved to be robust and efficient via several numerical examples. After the concept of discrete geometric conservation law (DGCL) is introduced, the intrinsic mechanism of DGCL is analyzed through 2D model, which is the inequality between volume increment and the volume sweeping by the surfaces enclosing of mesh cell. The different implementations of DGCL which could be mainly categorized as area correction, area correction via assuming velocity of surface, velocity correction and volume correction are surveyed and their range of application and the existing problems are discussed. We found that the proposed volume correction method can satisfy the fluid-structure interface condition, and is also appropriate for multi-step temporal discrete schemes.

unstructured mesh; mesh deformation; unsteady flow; geometric conservation law; interface coupling

2016-01-16； Revised： 2016-02-17； Accepted： 2016-05-03； Published online： 2016-05-1015:25

National Natural Science Foundation of China (91541117)

. Tel.： 0411-84707176E-mail: liujun65@dlut.edu.cn

2016-01-16； 退修日期： 2016-02-17； 录用日期： 2016-05-03；

时间： 2016-05-1015:25

www.cnki.net/kcms/detail/11.1929.V.20160510.1525.004.html

国家自然科学基金 (91541117)

.Tel.： 0411-84707176E-mail: liujun65@dlut.edu.cn

10.7527/S1000-6893.2016.0141

V211.3

A

1000-6893(2016)08-2395-13

引用格式： 刘君， 刘瑜， 陈泽栋． 非结构变形网格和离散几何守恒律[J]． 航空学报, 2016, 37(8): 2395-2407. LIU J, LIU Y, CHEN Z D. Unstructured deforming mesh and discrete geometric conservation law[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2395-2407.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160510.1525.004.html