一种形状可控的激波增强管道型线设计新方法

詹东文， 杨剑挺， 杨基明， 朱雨建

中国科学技术大学 近代力学系， 合肥　230027



一种形状可控的激波增强管道型线设计新方法

詹东文， 杨剑挺， 杨基明*， 朱雨建

中国科学技术大学 近代力学系， 合肥230027

激波管所产生的非定常运动激波，若强度和形状能够按照一定的设计要求进行可控条件下的调节，将可望为燃料点火燃烧试验等提供具有独到优势的研究手段。基于激波动力学理论，针对激波管中所产生的平面运动激波，通过设计特定的上下壁面收缩型线，使初始平面运动激波，经收缩段(包括光滑凹形曲线段、斜直线段和光滑凸形曲线段)的变形和强度增加，再以平面波面形状进入较小截面直管段的连续转变过渡，得到了强度增加的平面激波。进一步对所设计的典型型线分别采用数值计算和试验的方法，考核分析激波运动过程中的形状变化，验证了理论方法的可靠性。在此基础上，分析了型线设计的关键参数对激波增强幅度的影响，结果表明,相对于传统激波管方法，本文中所提出的收缩截面方法能更显著地增加平面激波强度；另外，还考察了初始入射激波马赫数对壁面型线和运动激波波面形状的影响，结果表明，对于较强的初始入射激波来说，壁面型线对入射激波强度依赖较小，也就是说，当实际入射激波马赫数即使稍偏离设计状态时，仍然能得到近乎完美的平面形状增强激波。

激波动力学； 激波管； 激波增强； 收缩管道； 壁面型线； 激波面形状

激波管和激波风洞是与飞行器尤其是高超声速飞行器研究密切相关的脉冲型地面模拟设备。其中，不管是为了模拟飞行器高焓流动还是开展燃料点火特性研究，都会遇到强激波的产生和准确控制等问题[1-8]。激波管中调节激波强度的一般方法是改变驱动段与被驱动段的压比，但生成的激波强度有限，当被驱动段不能抽真空时，这种限制尤为突出[9]。通过面积收缩的方法能较容易地增加激波强度[10-13]，如Bond等[10]通过一个线性汇聚的楔形结构研究了初始平面激波的聚焦增强特性。然而一般的截面变化会伴随着复杂扰动，导致沿激波面或跟随波后的参数分布不均匀，使生成的激波形状和强度偏离所需的试验状态。

为了避免截面改变所伴随的复杂扰动，作者所在课题组前期根据激波动力学理论[14-17]，在激波管中设计特定的凹形壁面型线，初始平面激波经过时壁面产生连续的“激波-压缩”扰动沿着激波传播，使平面激波平滑过渡为圆柱形汇聚激波[18-19]。但是生成的激波不断汇聚加强，无法稳定在试验所需的单一强激波状态。为了克服这一局限性，本文提出了一种可控的增加平面激波强度的收缩截面设计新方法，在凹形壁面型线的下游进一步设计特定的凸形壁面型线，使之产生的连续“激波-膨胀”扰动与上游传播过来的“激波-压缩”扰动刚好相反，逐渐抵消上游扰动对激波形状的影响，使弯曲激波恢复成试验所需状态的平面强激波，且波面上没有明显干扰。

本文为保证相对完整性，首先简单介绍了作为理论基础的激波动力学理论，继而设计出收缩段所应遵守的壁面控制型线，以使得进入该收缩段的平面初始激波在经过连续变形和强度增加之后，到达收缩段的出口时还能恢复到平面的波面形状。最后采用数值计算方法和纹影试验方法，考核分析该理论所设计的典型构型，并研究壁面型线设计的几个关键参数对平面激波增强效果的影响，以及对壁面型线形状和运动激波波面形状的影响。

1　激波动力学理论

激波动力学理论能够描述运动激波在变截面管道中的运动以及参数变化。如图1所示，应用正交曲线坐标系描述激波的运动，实线表示运动到不同时刻的激波位置，正交于激波位置的虚线称为“射线”。在曲线坐标系(α，β)中，同一时刻激波位置的α值相等，同一射线上的β值相等。相邻激波位置α和α+δα之间的距离为Ma(α，β)δα；相邻射线β和β+δβ之间的距离为A(α，β)δβ，如图中阴影区所示，由几何关系得[14-15]

(1)

式中：Ma为激波马赫数；A为管道面积。

当激波运动在相邻的两条射线之间时，可以近似将射线看做固壁。假设激波强度的变化只与管道面积有关，Chester (1954)[16]、Chisnell (1957)[17]和 Whitham (1957)[15]基于不同的途径得到相同的关系式(因此被称为CCW关系)，即

(2)

式中：

(3)

(4)

其中：γ为气体的比热比。

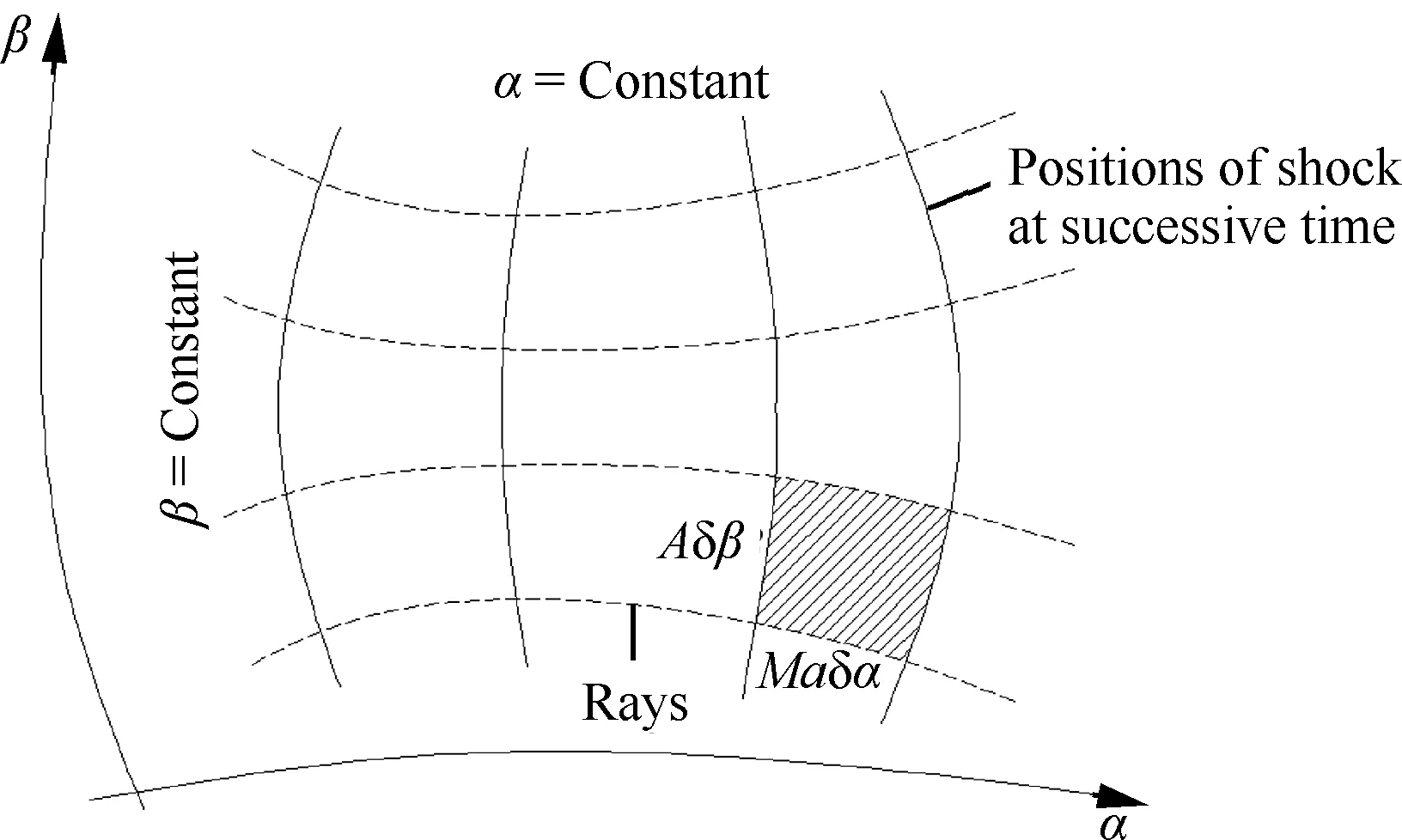
图1　不同位置的激波形状示意图Fig.1　Schematic of shock front at successive positions

激波在连续变截面管道中运动时，壁面产生连续的扰动沿着激波波面传播。凹形壁面产生“激波-压缩”扰动，凸形壁面产生“激波-膨胀”扰动。不考虑二次反射，可以得到扰动传播的特征线方程。进行坐标变化，得到笛卡儿坐标系下的方程为[14-15]

(5)

(6)

式中：θ为激波法向与水平方向的夹角；c(Ma)为连续扰动在激波上的传播速度，其表达式为

(7)

对于简单波区，特征线方程为

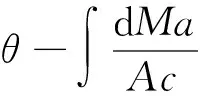
(8)

上述激波动力学理论在过去的研究中，主要用于给定几何边界条件来快速求解绕射激波形状[14-15]。本文的不同点是，进一步采用反设计的方法，由期望获得的激波形状和强度，逆向求解所需壁面型线的收缩截面构型。

2　型线设计方法

图2　壁面型线设计示意图Fig.2　Schematic drawing of wall profile

所设计的壁面型线收缩段的示意图如图2所示，其中A1B1C1D1(A2B2C2D2)表示产生圆弧形汇聚激波的壁面型线，上下壁面对称；红色实线表示不同时刻的激波位置，收缩段中间的斜线段表示特征线。当初始平面激波进入收缩段时，波前气体静止，光滑凹形壁面(A1B1B2A2)产生连续的“激波-压缩”扰动，沿着激波自底部向中间传播，改变激波形状使激波底部一直与壁面保持垂直，平面激波平滑转换为弯曲激波。在B1B2位置，激波刚好转换成曲率和强度都均匀的圆柱形激波。在斜直线壁面(B1C1C2B2)上，柱形激波维持圆弧形进行汇聚，波面曲率半径均匀减小，激波强度不断增加。

弯曲激波传播到光滑凸形壁面(C1D1D2C2)时，壁面产生连续的“激波-膨胀”扰动，沿着激波自底部向中间传播，其作用与上游传播过来的“激波-压缩”扰动刚好相反，逐渐抵消上游扰动对激波形状的影响，使弯曲激波面曲率减小。最终在收缩段的出口D1D2位置恢复为增强的平面激波，且激波波面上没有明显扰动。

根据上述平面激波增强原理，给定收缩段几个关键位置的激波形状、初始激波马赫数、激波管初始高度、收缩段的出口高度、汇聚角以及试验气体的比热比，可以通过求解反问题，得出收缩段的型线坐标。首先，已知初始激波马赫数、收缩段初始高度和出口高度，由CCW关系式(2)～式(4)得到收缩段的出口位置激波马赫数。其次，在单波区AiOBi(DiGCi)(i=1,2)，由单波区关系式(8)，根据激波角的变化得到点Bi(Ci)的激波马赫数；由CCW关系以及点Bi(Ci)在斜线段上，得到点Bi(Ci)的坐标，进一步得到柱形激波面B1B2(C1C2)上各点的激波马赫数、坐标位置和激波角。接着，在双波区B1B2O(C1C2G)，由双波区关系式(5)和式(6)，迭代求出双波区任一点的激波马赫数、坐标位置和激波角。最后，在单波区AiOBi(DiGCi)，已知双波区与单波区边界OBi(GCi)上各点的参数，由单波区关系式(8)，迭代求出型线AiBi(CiDi)上任一点的坐标。

上游的凹形壁面(A1B1B2A2)与下游的凸形壁面(C1D1D2C2)相比，虽然同样基于激波动力学理论求解壁面型线坐标，但改变激波形状的机理不同：前者生成连续“激波-压缩”扰动，而后者生成“激波-膨胀”扰动。另外，下游凸形壁面的设计要求“消除波面扰动”，刚好抵消上游扰动对激波形状的影响，才能得到激波面上没有明显扰动的平面激波。

3　结果与讨论

3.1设计结果

为了考核本文方法的可行性和可靠性，这里给出一个收缩段壁面型线的典型示例。设计条件为：初始入射平面激波马赫数Ma0=3.2，激波管的初始高度h=70 mm，收缩段出口的高度hmin=8 mm，汇聚角θ0=20°，试验气体为空气。得到的型线形状如图3所示，其中凹形壁面的水平长度为139.8 mm，截面高度由70 mm汇聚为30.6 mm；凸形壁面水平长度为21.5 mm，截面高度由17.4 mm过渡到8 mm；斜线段平滑连接凹形壁面和凸形壁面，水平长度为18.1 mm，汇聚角为20°。在此基础上，针对所设计的收缩壁面型线分别采用数值仿真和试验的方法进行验证。

试验使用截面为70 mm×40 mm的水平矩形激波管，驱动段管长为2.5 m，被驱动段管长为1.5 m。试验段剖视图如图3所示，显示了试验段侧壁观察窗和壁面型线的相对位置，其中绿色方框表示观察窗位置，观察范围包括长度为150 mm 的收缩段后半段和长度为20 mm收缩段出口。利用高速摄影机(Phantom V710)结合传统的纹影法，拍摄了激波在收缩段的传播过程，相邻图片之间的时间间隔为10 μs，曝光时间为1 μs，空间分辨率是384像素×152像素。数值方法运用二维轴对称VAS2D程序[20]，该算法采用非结构四边形网格，有限体积法，基于MUSCL-Hancock格式实现空间二阶和时间二阶精度。对参数变化剧烈的复杂流场区域采用网格自适应技术进行局部加密，该程序在求解激波传播等问题中已得到很好的验证[20]。数值计算所用的收缩段模型和计算参数与试验一致，网格初始尺寸为1 mm×1 mm的四边形，在收缩段的出口约为0.1 mm×0.1 mm的四边形，激波等参数变化剧烈区域最高加密5层，流场初始压力为一个标准大气压，试验气体初始静止，故壁面附近不出现激波边界层干扰现象。

图4给出了试验段中不同时刻激波位置的试验和数值结果。初始平面激波进入收缩段，首先运动在光滑凹形壁面上(0～90 μs)，激波波面形状自底部向中心逐渐弯曲，直到激波转变为波面曲率均匀的柱形激波(90 μs)。接着，激波在斜直线壁面上维持圆弧形进行汇聚。弯曲激波传播到光滑凸形壁面时(100～110 μs)，激波波面曲率自中心向底部逐渐减小，最终在收缩段的出口位置转变为平面激波(110 μs+)。接着，无明显干扰的平面激波在较小直管道中维持平直形状运动(110～120 μs)。可以看出，在整个运动过程中，激波形状一直保持平滑变化，到达收缩段出口时激波恢复到近乎完美的平面形状，试验和数值结果也相一致。

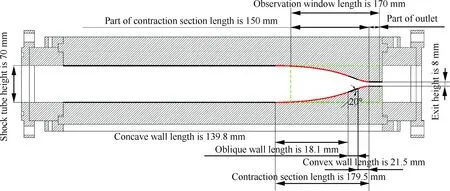
图3　试验段剖视图(侧壁)Fig.3　Cutaway view of test section (side wall)

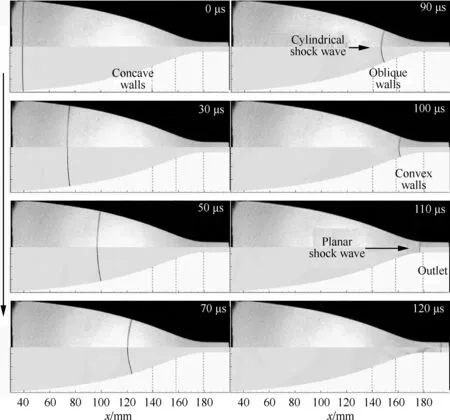
图4　试验段中激波的非定常运动特性(每幅图中上半部分是试验纹影，下半部分是数值纹影)Fig.4　Unsteady characteristics of shock wave in test section (upper part is test schlieren and lower part is numerical schlieren in each image)

分别提取试验纹影和数值纹影中不同时刻的激波波面形状，与相应位置的理论激波形状进行对比，如图5所示。在不同时刻，试验、数值与理论的激波波面形状都符合得比较好，说明在一定程度上，理论设计方法可以精确控制激波波面形状的变化。由110～120 μs时段中激波运动的距离，可以近似求出收缩段出口位置的激波马赫数MaD=4.80；通过CCW关系式(2)～式(4)，求出的MaD=4.83，可见二者吻合得很好，这就验证了理论设计方法的可行性与可靠性。

为了验证理论设计方法的有效性和必要性，这里给出一个反例构型来说明随意的凹-凸型线难以起到消波作用。将上述弯曲壁面替换成相应的圆弧形壁面，壁面各点坐标位置和汇聚角度尽量相近。通过数值仿真的方法对比分析这两种构型中的激波波面形状的变化，如图6所示，激波位于较小直管道中(120 μs)，图片下半部分是理论方法设计的特定型线，上半部分是替换的圆弧形型线。由图可知，图片上半部分的流场中明显出现了沿激波波面横向传播的强扰动，使激波波面出现明显弯折。定义激波面的最大弯曲度为最大弯曲位置的弦长与该处到临近壁面垂直高度的比值。则上半部分激波面的最大弯曲度为8.37%。而在图片下部分的流场中，较小直管道中扰动不明显，激波面最大弯曲度为0.85%，激波波面近乎完美的平直形状，说明凸形型线有效地保持了激波波面的均匀性，进一步验证了理论设计方法的有效性和必要性。

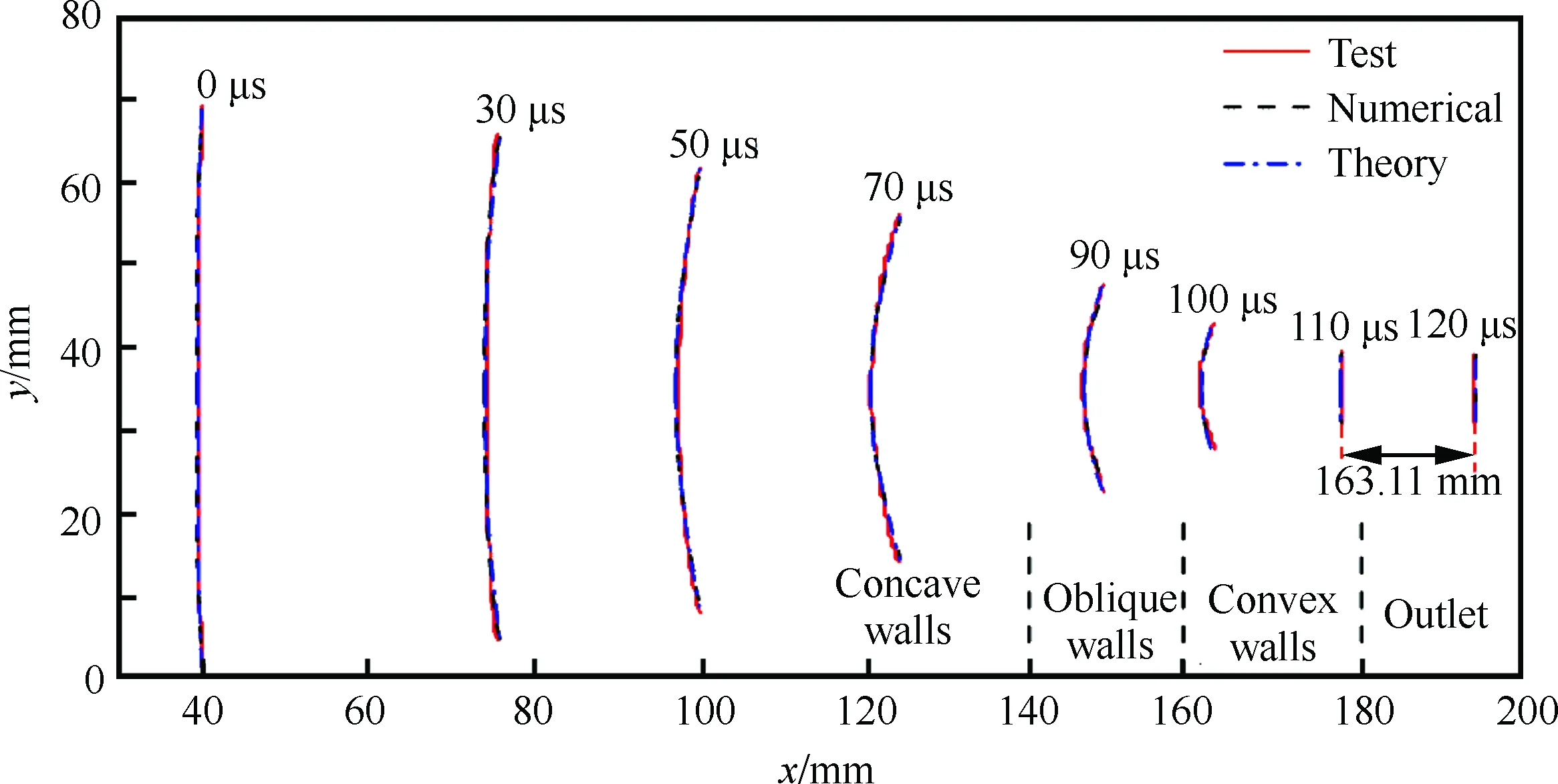
图5　不同时刻的激波波面形状对比Fig.5　Comparison of shock wave front at different moments

图6　壁面型线的数值对比 (下半部分是理论方法设计的型线，上半部分是替换的圆弧型线)Fig.6　Numerical comparison of wall profiles (lower part is designed wall profile andupper part is replaced with circular arc wall profile)

3.2平面激波增强效果

收缩段出口位置的激波强度是本文关注的焦点。由CCW关系式(2)可知，收缩段出口的激波马赫数MaD与初始激波马赫数Ma0、收缩比h/hmin和比热比γ有关。为了便于具体比较和分析，这里给出典型示例如图7中实线所示，其中Ma0=3.2，γ=1.4。可以看出，随着h/hmin的增加，MaD增加较快。当收缩比h/hmin增加到103时，出口的激波马赫数达到了12以上。图中同时对比了传统的激波管中，通过增加驱动压比的方法对激波的增强效果，如虚线所示。随着激波管驱动压比的增加，MaD也有所增加，但趋势明显减缓。在空气驱动空气的情况下，即使压比接近于无穷大，MaD也仅能达到6左右。而采用本文的方法，获得该强度的激波所需要的收缩比仅为26。由此可见，本文方法不失为增加平面激波强度的一条有效途径。

图7　控制参数对收缩段出口马赫数MaD的影响Fig.7　Influence of control parameters on exit of contraction Mach number MaD

3.3参数对型线和激波形状的影响

3.3.1对型线形状的影响

由前文型线设计方法可知，随着初始入射激波强度和平面激波增强幅度的不同，需要相应调整壁面的型线形状。因此，有必要了解和掌握初始控制参数对壁面型线的影响。由于上下壁面对称，仅以下壁面的型线A1B1C1D1为例进行说明。如图8所示，凸形型线的横坐标起点都为零。随着初始激波马赫数Ma0的增加，凸形型线和凹形型线的长度均略有减小，且减小的幅度随Ma0的上升而趋于微弱。由图8(a)可以看出当Ma0>3.2时，型线的改变已不明显。另一方面，激波增强幅度的大小主要通过截面收缩比来控制。由图8(b)可知，当收缩比h/hmin增大时，型线的长度将随之缩短。

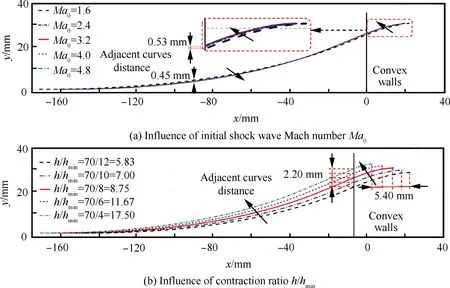
图8　控制参数对壁面型线的影响Fig.8　Influence of control parameters on designed profile

3.3.2对激波形状的影响

设计初始激波马赫数Ma0较大(例如大于3.2)时，壁面的型线虽然变化很小，但试验中初始入射激波马赫数Ma0偏离设计值可能会造成激波汇聚过程波面形状的些许变化。图9给出了相同型线上不同Ma0的激波运动情况，所用型线的设计Ma0=3.2，从左到右的4幅图分别是激波位于凹形型线段、斜线段、凸形曲线段和收缩段出口的激波形状，各图纵横坐标尺度一致。由图9可知，位于凹形型线时，较大Ma0的激波底部超前，而较小Ma0的滞后，这是由于Ma0越大，激波波面底部相对于中间的加速幅度越大；与之相反，位于凸形型线时，Ma0越大，激波波面底部相对于中间的加速幅度越小，越快恢复到平直形状。在斜线段上，激波都保持近乎完美的圆弧形形状。在较小直管道中，激波面都近乎完美的平直形状，最大弯曲度稍微变化，即使在激波弯曲较严重的Ma0=4.0时，其最大弯曲度也仅为1.73%，且流场中也没有明显扰动。

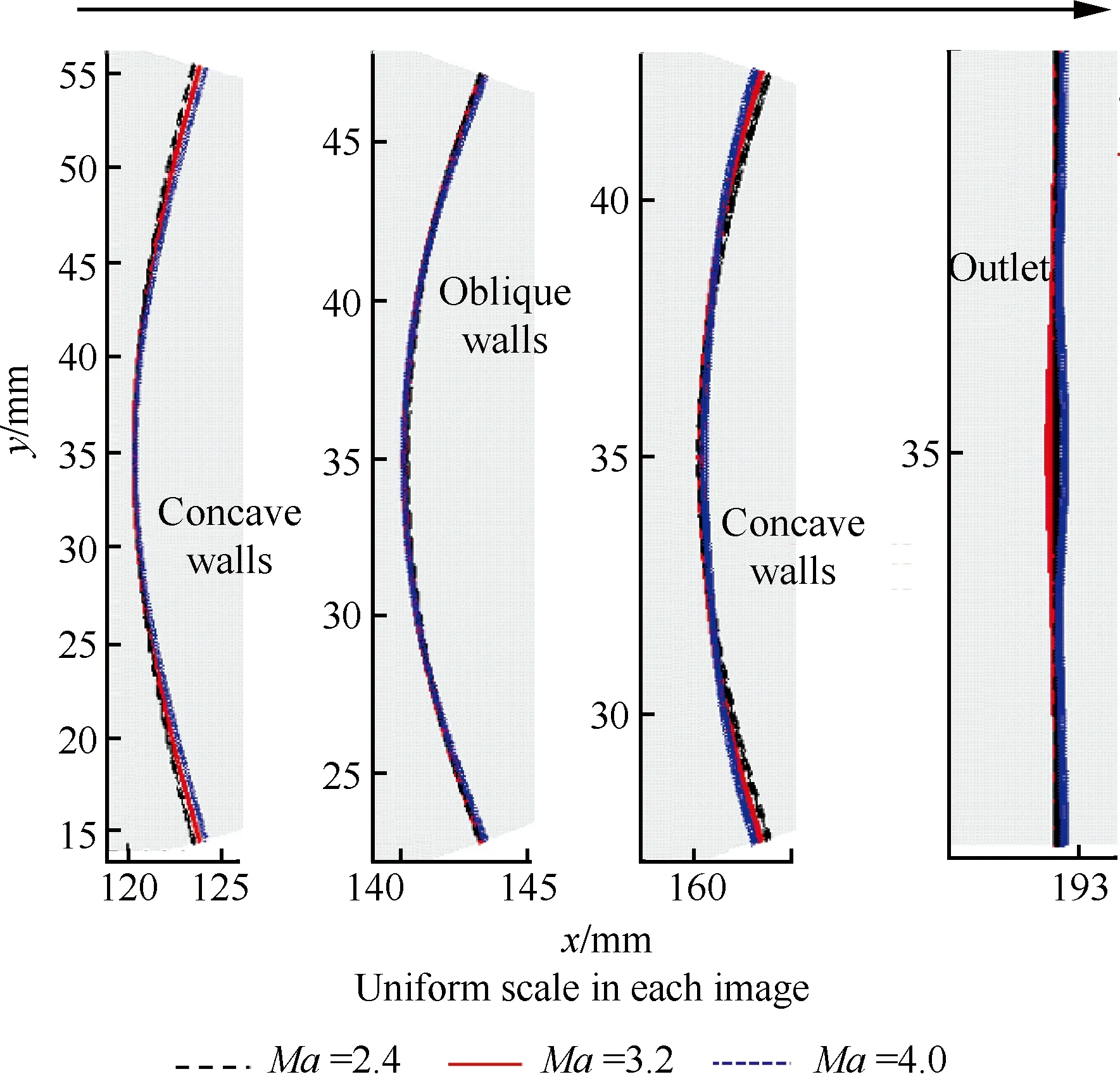
图9　控制参数对激波波面形状的影响(设计Ma0=3.2)Fig.9　Influence of control parameters on shock wave shape (designed Ma0=3.2)

4　结　论

1) 基于激波动力学理论，提出了一种凹形-凸形收缩壁面型线的设计方法，以使得进入该收缩段的平面初始激波在经过连续变形和强度增加之后，到达收缩段出口时还能恢复到平面的波面形状。初始平面激波经过光滑凹形壁面时，壁面产生连续的“激波-压缩”扰动沿着激波波面传播，使平面激波平滑过渡为圆柱形汇聚激波。斜直线段作为过渡段使柱形激波均匀汇聚。弯曲激波经过下游的光滑凸形壁面时，壁面产生的连续“激波-膨胀”扰动，与上游产生的“激波-压缩”扰动刚好相反，使弯曲激波恢复成试验所需的增强的平面激波。

2) 采用数值计算和纹影试验的方法，针对该理论所设计的典型收缩型线，考核分析了激波的非定常运动特性。结果表明，到达收缩段出口时，激波恢复到近乎完美的平面形状，从而验证了该理论方法的可行性与可靠性。另外，通过替换的光滑圆弧壁面型线作为反例，发现收缩段出口激波波面出现突起，波面形状发生明显弯折，从反面验证了本文理论方法的有效性和必要性。

3) 分析了控制型线设计的几个关键参数对平面激波增强过程的影响。结果表明，相对于传统的激波管增加高、低压段压比的方法而言，本文的收缩截面方法能更高效地增加平面激波的强度。此外，尽管壁面型线设计依赖于初始的入射激波强度，但对设计Ma0较大的稍强激波来说，随着Ma0的增加壁面型线变化微弱，因此，即使Ma0与设计条件略有偏离，也能得到近乎完美的平面形状的增强激波。

[1]张若凌, 乐嘉陵, 王苏, 等. 强激波阵面的非平衡特性研究[J]. 实验流体力学, 2006, 20(2): 36-49.

ZHANG R L, LE J L, WANG S, et al. The research of nonequilibrium characteristics of strong shock front[J]. Journal of Experiments in Fluid Mechanics, 2006, 20(2): 36-49 (in Chinese).

[2]高云亮, 李进平, 胡宗民, 等. 准定常强激波马赫反射波形的数值研究[J]. 空气动力学学报, 2008, 26(4): 456-461.

GAO Y L, LI J P, HU Z M, et al. A numerical investigation on the Mach reflection patterns of quasi-steady strong shock waves[J]. Acta Aerodynamica Sinica, 2008, 26(4): 456-461 (in Chinese).

[3]MATSUMOTO Y, AMANO T, KATO T N, et al. Stochastic electron acceleration during spontaneous turbulent reconnection in a strong shock wave[J]. Science, 2015, 347(6225): 974-978.

[4]KJELLANDER M, TILLMARK N, APAZIDIS N. Shock dynamics of strong imploding cylindrical and spherical shock waves with real gas effects[J]. Physics of Fluids, 2010, 22(11): 116102-1-7.

[5]吴子牛, 白晨媛, 李娟, 等. 高超声速飞行器流动特征分析[J]. 航空学报, 2015, 36(1): 58-85.

WU Z N, BAI C Y, LI J, et al. Analysis of flow characteristics for hypersonic vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 58-85 (in Chinese).

[6]SRIRAM R, JAGADEESH G. Correlation for length of impinging shock-induced large separation bubble at hypersonic speed[J]. AIAA Journal, 2015, 53(9): 2771-2775.

[7]RAGA A C, CANTO J, RODRIGUEZ L F, et al. An analytic model for the strong-/weak-shock transition in a spherical blast wave[J]. Monthly Notices of the Royal Astronomical Society, 2012, 424(4): 2522-2527.

[8]邱华, 王玮, 范玮, 等. U型方管中爆燃向爆震转变特性实验研究[J]. 航空学报, 2015, 36(6): 1788-1794.

QIU H, WANG W, FAN W, et al. Experimental investigation on characteristics of deflagration to detonation transition in U-bend square tube[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1788-1794 (in Chinese).

[9]ZHAI Z G, WANG M H, SI T, et al. On the interaction of a planar shock with a light polygonal interface[J]. Journal of Fluid Mechanics, 2014, 757(2): 800-816.

[10]BOND C, HILL D J, MEIRONAND D I, et al. Shock focusing in a planar convergent geometry: Experiment and simulation[J]. Journal of Fluid Mechanics, 2009, 641(12): 297-333.

[11]WANG C X, GRUNENFELDER L K, PATWARDHAN R, et al. Investigation of shock wave focusing in water in a logarithmic spiral duct, Part 2: Strong coupling[J]. Ocean Engineering, 2015, 102: 185-196.

[12]DIMOTAKIS P E, SAMTANEY R. Planar shock cylindrical focusing by a perfect-gas lens[J]. Physics of Fluids, 2006, 18(3): 031705-1-4.

[13]HOSSEINI S H R, TAKAYAMA K. Experimental study of toroidal shock wave focusing in a compact vertical annular diaphragmless shock tube[J]. Shock Waves, 2010, 20(1): 1-7.

[14]HAN Z Y, YIN X Z. Shock dynamics[M]. Berlin: Springer, 1993: 21-67.

[15]WHITHAM G B. A new approach to problems of shock dynamics. Part I. Two-dimensional problems[J]. Journal of Fluid Mechanics, 1957, 2(2): 145-171.

[16]CHESTER W. The quasi-cylindrical shock tube[J]. Philosophical Magazine, 1954, 45(371): 1293-1301.

[17]CHISNELL R F. The motion of a shock wave in a channel with applications to cylindrical and spherical shock waves[J]. Journal of Fluid Mechanics, 1957, 2(3): 286-298.

[18]ZHAI Z G, LIU C L, QIN F H, et al. Generation of cylindrical converging shock waves based on shock dynamics theory[J]. Physics of Fluids, 2010, 22(4): 041701-1-3.

[19]ZHAI Z G, SI T, LUO X S, et al. Parametric study of cylindrical converging shock waves generated based on shock dynamics theory[J]. Physics of Fluids, 2012, 24(2): 026101-1-12.

[20]SUN M, TAKAYAMA K. Conservative smoothing on an adaptive quadrilateral grid[J]. Journal of Computational Physics, 1999, 150(1): 143-180.

詹东文男， 博士研究生。主要研究方向： 激波动力学。

Tel.: 0551-63601242

E-mail: zhandw@mail.ustc.edu.cn

杨剑挺男， 博士研究生。主要研究方向： 空气动力学。

Tel.: 0551-63601242

E-mail: yjt779@mail.ustc.edu.cn

杨基明男， 博士， 教授， 博士生导师。主要研究方向： 高超声速飞行器相关试验与数值计算， 多相流试验与测量， 仿生生物流体力学。

Tel.: 0551-63603390

E-mail: jmyang@ustc.edu.cn

朱雨建男， 博士， 副教授， 硕士生导师。主要研究方向： 空气动力学， 多相流。

Tel.: 0551-63603390

E-mail: yujianrd@ustc.edu.cn

A new method of wall profile design for shape-controllable shockwave enhancement

ZHAN Dongwen, YANG Jianting, YANG Jiming*, ZHU Yujian

Department of Modern Mechanics, University of Science and Technology of China, Hefei230027, China

The generation of shape and strength controllable shock wave will offer a special way for ignition and combustion experiments. In this paper, a new method has been proposed for smooth enhancement of a shock wave in a shock tube. With the help of shock dynamics theory, a planar-to-planar shock wave enhancement can be obtained through a convergent channel of specially designed smooth concave-convex wall contour, which bends the planar incoming shock wave into a cylindrical convergent one and then planarizes it and finally forms a strengthened planar shock wave. A typical designed wall profile is verified with both numerical simulation and experimental test. It is found that the agreement of shock wave shape is nearly perfect. Furthermore, the influence of some dominant parameters on the shock enhancement process is analyzed. Compared to the traditional way of increasing pressure ratio in a shock tube, the new method is more efficient to increase plane shock wave intensity. Meanwhile, the influences on wall profile and shock front shape are also performed. When the initial shock is relatively strong, the designed wall profile almost remains the same even though the incoming shock Mach number deviates to some extent, which means that a near-perfect straight shape of shock front can be obtained regardless of unavoidable experimental scatters.

shock dynamics; shock tubes; shock wave enhancement; convergent channel; wall profile; shock front shape

2016-01-11； Revised： 2016-02-17； Accepted： 2016-03-08； Published online： 2016-03-2113:27

National Natural Science Foundation of China (11132010)

. Tel.： 0551-63603390E-mail: jmyang@ustc.edu.cn

2016-01-11； 退修日期： 2016-02-17； 录用日期： 2016-03-08；

时间： 2016-03-2113:27

www.cnki.net/kcms/detail/11.1929.V.20160321.1327.010.html

国家自然科学基金 (11132010)

.Tel.： 0551-63603390E-mail： jmyang@ustc.edu.cn

10.7527/S1000-6893.2016.0071

V211.751; O354.5

A

1000-6893(2016)08-2408-09

引用格式： 詹东文， 杨剑挺， 杨基明， 等. 一种形状可控的激波增强管道型线设计新方法[J]. 航空学报, 2016, 37(8): 2408-2416. ZHAN D W, YANG J T, YANG J M, et al. A new method of wall profile design for shape-controllable shock wave enhancement[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2408-2416.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160321.1327.010.html