高超声速进气道强制转捩流动的大涡模拟

赵晓慧, 邓小兵，*, 毛枚良, 杨伟, 赵慧勇

1.中国空气动力研究与发展中心 空气动力学国家重点实验室， 绵阳　621000 2.中国空气动力研究与发展中心 计算空气动力研究所， 绵阳　621000 3.中国空气动力研究与发展中心 高超声速冲压发动机重点实验室， 绵阳　621000



高超声速进气道强制转捩流动的大涡模拟

赵晓慧1, 邓小兵1，*, 毛枚良2, 杨伟1, 赵慧勇3

1.中国空气动力研究与发展中心 空气动力学国家重点实验室， 绵阳621000 2.中国空气动力研究与发展中心 计算空气动力研究所， 绵阳621000 3.中国空气动力研究与发展中心 高超声速冲压发动机重点实验室， 绵阳621000

吸气式高超声速飞行器常在进气道边界层内布置粗糙颗粒或涡流发生器强制流动转捩为湍流以确保发动机正常启动。为了清晰认识强制转捩过程，采用隐式大涡模拟方法，对强制转捩问题开展了数值模拟研究。针对钻石形和斜坡形涡流发生器，计算得到涡流发生器诱导的流动结构，显示出强制转捩流动由涡流发生器产生的反向旋转流向涡对主导。扰动沿流向增长和发展，导致流向涡对以偶模式或奇模式失稳，偶模式失稳产生对称形式的涡对破碎，而奇模式失稳则导致非对称(弯曲)形式的涡对破碎。流向涡对破碎后产生一系列发卡涡并最终促使边界层转捩为湍流。最后就计算网格和数值耗散对隐式大涡模拟结果的影响以及计算的收敛性进行了讨论。

高超声速； 进气道； 强制转捩； 涡流发生器； 大涡模拟

吸气式高超声速飞行器通常巡航在高度比较高，而密度则相对较低的大气环境中，此时飞行雷诺数相对较小，自然转捩发生的位置通常超出了进气道长度。为了满足发动机设计对边界层湍流流态的要求，需要在进气道采用强制转捩措施。2004年，Hyper-X (X-43A)采用涡流发生器在飞行试验中成功实现了强制转捩[1]，测试结果显示，对于马赫数7和10的飞行条件，飞行器前体需要采用粗糙带来保证进气道上游的全湍流状态。

涡流发生器强制转捩的作用机理图像尚未完全清晰，最早的一些研究者试图用Tollmien-Schlichting (T-S)波解释粗糙颗粒强制转捩机理[2]，Reshotko和Tumin[3]则认为瞬时增长在粗糙颗粒强制转捩中起了重要作用。数值计算结果显示强制转捩过程与涡流发生器产生的流向涡对的发展有关，这与Görtler涡的二次失稳相似，在文献[4]中这种粗糙颗粒引起的流向反向旋转的涡对也被称作Görtler涡。Li等[5-6]在研究低速和高速流动Görtler涡时指出其二次失稳主要有奇模式(Odd mode)和偶模式(Even mode)两种，分别导致了弯曲(Sinuous)和对称(Varicose)两种不同形式的流向涡对破碎，并且其不稳定模式与Görtler涡波长有关。Tullio等[7]利用线性稳定性理论以及求解Navier-Stokes方程研究超声速平板利用颗粒强制转捩时也指出，对称和弯曲是两种最容易出现的不稳定形态。

高超声速边界层的涡流发生器强制转捩过程受涡流发生器的形状、尺寸、分布和环境噪声等诸多因素的影响。Berry等[8-10]对五种形状的涡流发生器作了试验比较，发现钻石形和斜坡形涡流发生器具有较好的转捩触发效果。赵慧勇等[11]在中国空气动力研究与发展中心的FL-31(直径0.5 m)超声速风洞中，开展了钻石形和斜坡形涡流发生器强制转捩研究，给出了钻石形涡流发生器触发转捩的有效高度。Danehy等[12]采用平面激光诱导荧光(Plane Laser-Induced Fluorescence, PLIF) 技术研究了平板表面半球凸起物对边界层的影响，冈敦殿等[13]采用基于纳米示踪的平面激光散射技术(Nano-tracer Planar Laser Scattering, NPLS)进行了超声速平板上直立圆台凸起物绕流流场研究，张庆虎[14]采用NPLS技术对三角楔涡流发生器产生的流动结构给过较为细致的展示，这些研究都给出边界层中突起物尾迹某一平面上的精细结构，对研究突起物尾迹的发展有很大帮助。Borg和Schneider[15]在静声风洞中开展了X-51前体强制转捩研究，指出来流噪声会使转捩位置提前；邓小兵[16]采用隐式大涡模拟(Implicit Large Eddy Simulation, ILES)方法，通过在计算来流中加噪声信号来模拟试验条件，发现相同的现象。这表明，要通过试验准确预测转捩位置需采用静声风洞以消除风洞噪声的影响。

相比于试验研究，数值计算可以获得更为全面的流场信息，而且不受风洞噪声的影响。研究强制转捩问题采用的数值模拟方法主要有直接数值模拟(Direct Numerical Simulation, DNS)，大涡模拟(Large Eddy Simulation, LES)和雷诺平均Navier-Stokes(RANS)方程方法。其中，DNS方法最准确，Marxen[17]、Iyer[18]和Duan[19-20]等利用DNS对突起物强制转捩流动进行研究，获得了清晰的流动结构和转捩图像。DNS方法的缺点是所需的计算资源过多，在当前的计算机硬件条件下还难以推广应用。涂国华等[21]曾经利用RANS方法对强制转捩流动进行模拟，结果表明RANS方法难以预测转捩位置，且对转捩后压缩面上热流分布的预测也不理想。周玲等[22-23]改进了k-ω-γ转捩模式，并对高超声速飞行器进气道前体边界层强制转捩进行数值计算，指出改进模型对转捩位置有较好的预测能力。然而采用RANS方法难以准确捕捉强制转捩的流动结构。LES方法能够以远低于DNS的计算开销给出较为准确的非定常流动结构。Sayadi和Moin[24]利用大涡模拟方法对马赫数0.2可压缩平板边界层的H-type和K-type转捩进行了模拟，指出涡黏性在层流和转捩区的存在会阻碍扰动的发展，不利于转捩预测。ILES不加入亚格子模型，在层流区不会引入亚格子耗散，能够更准确地模拟转捩区的扰动增长。Orlik和Fedioun[25]采用基于5阶WENO格式的隐式大涡模拟方法计算了射流控制的高超声速边界层强制转捩流动，结果显示ILES能够捕捉到丰富的流动细节。本文重点关注涡流发生器诱导强制转捩过程的模拟，因而采用ILES是合适的。

通常认为，大涡模拟方法需要采用高阶精度格式，邓小兵和金玲[26]通过对湍流数值模拟中误差传播和发展的动力学行为的分析，认为二阶精度为基础的数值方法可以应用于湍流大涡模拟。本文采用二阶有限体积隐式大涡模拟方法，对钻石形和斜坡形涡流发生器激发的高超声速进气道边界层转捩现象开展数值模拟研究，计算得到了流向涡失稳的两种基本模式：偶模式与奇模式，同时给出了脉动量沿流向的增长规律，最后对数值耗散和网格分辨率共同作用下ILES方法的收敛性作了探讨。

1　研究方法

1.1隐式大涡模拟方法

采用基于二阶有限体积的ILES方法研究强制转捩问题。由于ILES采用数值黏性模拟亚格子耗散，数值耗散的控制就十分重要。对流项空间离散格式的数值耗散对大涡模拟结果有明显的影响，过大的数值耗散往往导致能谱过度耗散，抑制不稳定波的初始增长，所以数值耗散的控制对转捩位置的准确预测至关重要。采用基于MUSCL( Monotone Upstream-centered Scheme for Conservation Laws)重构的ROE格式，在光滑区，该重构表达式退化为

(1)

式中：qL,i+1/2和qR,i+1/2分别为i和i+1单元界面变量左侧和右侧重构值；当κ=1/3时为常用的三阶格式，此时格式对ILES是过耗散的，κ=1时格式变为二阶中心格式，是无耗散的，通过调整κ可以将数值耗散控制在合理水平。高超声速流动中存在强激波，计算中对差商Δ-、Δ+采用min-mod限制器保证计算的鲁棒性[27]。黏性项离散采用二阶中心格式。非定常时间推进采用双时间步方法[28]，其中物理时间推进采用二阶欧拉后差格式，隐式时间推进采用LU-SGS方法[29]。

1.2算例验证

Duan等[30]开展了来流马赫数Ma=2.99的超声速湍流平板边界层DNS研究，这里用此算例验证所采用软件和方法的有效性。

算例来流密度ρ∞=0.089 1 kg/m3，来流温度T∞=218.2 K。计算域尺寸为：流向69 mm，展向35 mm，法向110 mm。计算网格单元量约900万，其中流向dx+=12，展向dy+=4.5，法向第一层网格dz+=0.3。壁面边界条件为无滑移等温壁，壁面温度Tw=567.3 K。计算入口边界层厚度为7.2 mm，入口边界采用时间平均剖面叠加瞬时脉动的方法，其中时间平均剖面采用RANS计算的结果，瞬时脉动采用RRM(Rescaling-Recycling Method)[31-32]将下游x=52 mm位置处的瞬时脉动按照边界层相似关系重新标定后叠加到入口边界。

物理模型采用基于改进延迟脱体涡模拟(Improved Delayed Detached-Eddy Simulation, IDDES)[33]方法的壁面模化大涡模拟(Wall-Modeled LES, WMLES)，其中湍流雷诺应力模型采用一方程Spalart-Allmaras(S-A)模型[34]，MUSCL重构耗散参数κ=0.8。

图1为计算得到的边界层平均速度剖面(时间平均加展向平均)。模拟结果与理论曲线以及文献[30]DNS模拟结果符合较好，这表明本文所用的软件和方法是可靠的。

图1　超声速平板边界层平均速度剖面计算结果Fig.1　Computational results of averaged velocity profile in supersonic flat boundary layer

2　模型与网格说明

计算采用的进气道模型是在赵慧勇等[11]试验模型基础上简化得到的，如图2所示。进气道为分段压缩结构，三个压缩面均与水平方向有一定夹角。水平方向从前缘指向下游定义为x正方向，竖直方向定义为y向，涡流发生器(Vortex Generators, VG)凸起方向大致为y的负方向，展向定义为z方向。z向取了试验模型中线附近的一小段，x向长度约300 mm。涡流发生器采用了钻石形和斜坡形两种，后缘大致放在x=88 mm的位置(当地边界层厚度约为1.2 mm)。计算域展向尺寸以及模拟涡流发生器的个数和高度见表1。

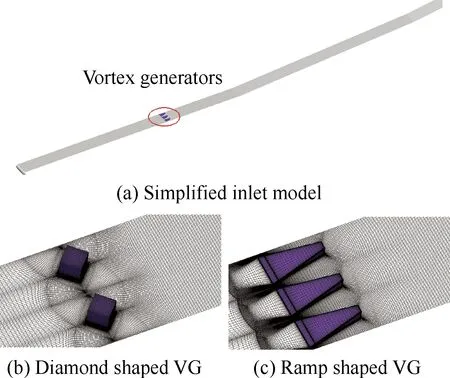
图2　进气道与涡流发生器模型及其网格(G1)Fig.2　Models and grids of inlet and vortex generators (G1)

表1　计算模型

Table 1　Computational models

CaseVGshapeComputationalwidth/mmVGnumberVGheight/mm1Diamond6.021.02Ramp5.730.5

考虑计算量，本文对钻石形的涡流发生器只模拟了两颗，对斜坡形的模拟了三颗。展向采用周期边界条件。为了更好地分辨关键区域的流动结构，加密了涡流发生器附近和尾迹等区域的网格，并采用G1和G2粗细两套网格计算考察了网格分辨率对计算结果的影响，这两套网格在包含主要流动结构的区域配置见表2。其中dx+为基于壁面单位的流向网格尺度，dz+为展向，dy+为法向，dy2+为法向第一层网格尺度。按照文献[35]给出的LES网格分辨率准则，表2给出的粗网格G1已经满足了LES模拟要求。

表2　计算网格

3　数值计算和分析

3.1计算条件

根据赵慧勇等的试验[11]，选用马赫数6试验中的两组试验参数作为计算工况。来流马赫数Ma=5.96，迎角α=1°，来流压力p∞，来流温度T∞以及第一、第二、第三压缩面的物面温度Tw1、Tw2、Tw3见表3。

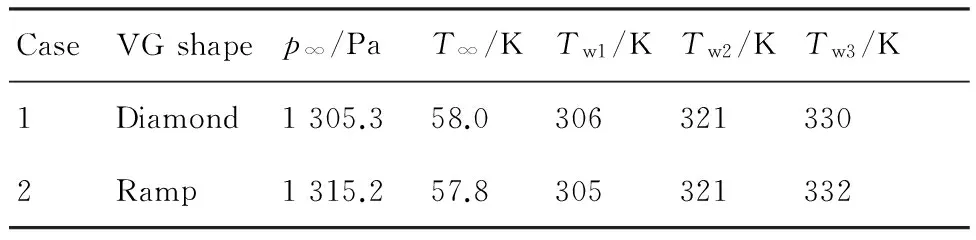
表3　计算条件

3.2涡流发生器产生的涡结构

利用大涡模拟，对两个工况进行模拟，获取了非定常流场结构。涡流发生器周围的涡结构如图3 所示。其中Q值定义为

(2)

式中：Ω为基于特征速度为来流声速和特征长度为1 mm的无量纲涡强；S为变形率张量。

图3　涡流发生器附近的流线和流场Q等值面Fig.3　Streamlines and Q iso-surfaces of flow around vortex generators

根据工况1的瞬时流场可以看出，在钻石形涡流发生器前缘根部产生了一个“马蹄”涡，同时在后缘产生一对反向旋转的流向涡。后缘产生的这对涡，其旋转方向与外侧的“马蹄”涡反向，而位置比外侧的“马蹄”涡要远离壁面一些，其强度也高于“马蹄”涡。工况2的瞬时流场显示，斜坡形的涡流发生器产生的涡结构相对简单，其主要结构是涡流发生器侧缘产生的一对反向旋转的流向涡，这对涡的结构、转向与工况1中钻石形涡流发生器后缘产生的流向涡相似。由于涡流发生器形状、高度和分布密度不同，这里两个工况中，钻石形涡流发生器产生的流向涡更强，斜坡形涡流发生器产生的涡对更密集。

3.3强制转捩过程分析

图4显示出钻石形涡流发生器下游的主导结构是尾缘产生的流向涡对。这对流向涡相互抬升，并在第二压缩面上破碎并脱落出一系列的“发卡”涡，“发卡”涡很大程度上加剧了流动内层和外层的流体交换，破坏了边界层的稳定性，促成转捩。图5显示出斜坡形涡流发生器主要流向涡对结构的发展，与钻石形涡流发生器强制转捩相似，斜坡形涡流发生器产生的流向涡对在第二压缩面破碎脱落产生“发卡”涡，促成转捩，明显有别于工况1的是，工况2中流动结构有展向的摇摆和弯曲，摇摆的频率与“发卡”涡脱落的频率是相关的。计算结果显示，涡流发生器促使流动转捩过程是其产生的流向涡对主导的，流向涡对结构失稳、破碎产生一系列“发卡”涡，使得边界层流动转捩为湍流。

图4　钻石形涡流发生器强制转捩瞬时流场Q等值面图(G1, κ=0.9)Fig.4　Q iso-surfaces of forced transition instantaneous flow by diamond shaped vortex generators (G1, κ=0.9)

图5　斜坡形涡流发生器强制转捩瞬时流场Q等值面图(G2, κ=0.9)Fig.5　Q iso-surfaces of forced transition instantaneous flow by ramp shaped vortex generators (G2, κ=0.9)

图6　沿流向涡物理量脉动的均方根Fig.6　Root-mean-square of variable fluctuations along a stream-wise vortex

两种涡流发生器强制转捩过程都与流向涡对结构的失稳有关。图7为瞬时流场中压力脉动p′沿流向涡对结构两个涡心的分布。图7(a)显示工况1瞬时流场中压力脉动相位相同，表明工况1流向涡对失稳由偶模式主导，这种模式导致流向涡对对称破碎；图7(b)显示工况2瞬时流场中压力脉动相位相反，表明工况2流向涡对失稳由奇模式主导，这种模式导致流向涡对弯曲破碎。

图7　瞬时流场沿流向涡对两个涡心的压力脉动分布Fig.7　Pressure fluctuation of instantaneous field distribution along two vortex centers of counter-rotating vortices

涡流发生器的几何参数和分布密度会影响流向涡对结构不稳定增长的主导模式、频率、破碎位置等，这些参数的具体影响有待深入研究。Li等[5-6]在研究Görtler涡二次失稳时指出，Görtler涡波长(展向)较大时二次失稳由偶模式主导，波长较小时更容易出现奇模式。文中工况1涡对之间的距离较远，对应的波长为3 mm，工况2中涡对之间的距离较近，波长为1.9 mm，文中两个工况在失稳模式和波长的对应关系上与Li等对于Görtler涡二次失稳的结论相符合。

3.4计算收敛性讨论

对于本文研究的涡流发生器强制转捩流动，流向涡对结构破碎的位置基本决定了转捩位置，准确模拟涡破碎位置取决于对扰动增长过程的准确模拟，而准确模拟扰动增长的关键则是避免数值耗散对其产生明显的抑制。因此，网格密度和数值方法所引入耗散的大小，是准确计算转捩位置的关键。本节通过对数值耗散和网格密度的调节，考察了本文所采用的数值方法的收敛性。

图8和图9给出了在G1和G2两套网格上计算结果随网格和耗散参数κ的变化，其中σp为压力均方根。本文以流向涡对破碎位置作为计算收敛的判断依据。涡破碎位置不仅受网格的影响，同样受到数值格式耗散的影响。大体趋势是网格越密、数值格式耗散越低，涡破碎位置越靠前，这是由于数值耗散能够抑制扰动的增长。随着格式耗散的降低和网格的加密，涡对破碎位置前移并趋于不变。如前所述，本文采用的粗网格G1满足LES模拟的需求[35]，如果一定的格式耗散(取决于κ值)下，涡破碎位置不再随网格加密变化，则可以认为数值方法是合适的。

从图8和图9中流向涡对破碎位置以及流场中脉动压力的增长看，在格式耗散较小(κ较大)的情况下，计算更容易达到网格收敛；κ=0.9时，G1和G2两套网格下计算得到的涡破碎位置几乎一致，可认为实现了网格收敛；对于文中两个工况，在G1网格下，采用κ=0.9计算基本得到了收敛的流向涡对破碎位置。

图8　第二压缩面上流场Q等值面图 Fig.8　Q iso-surfaces of flow on the second compress surface

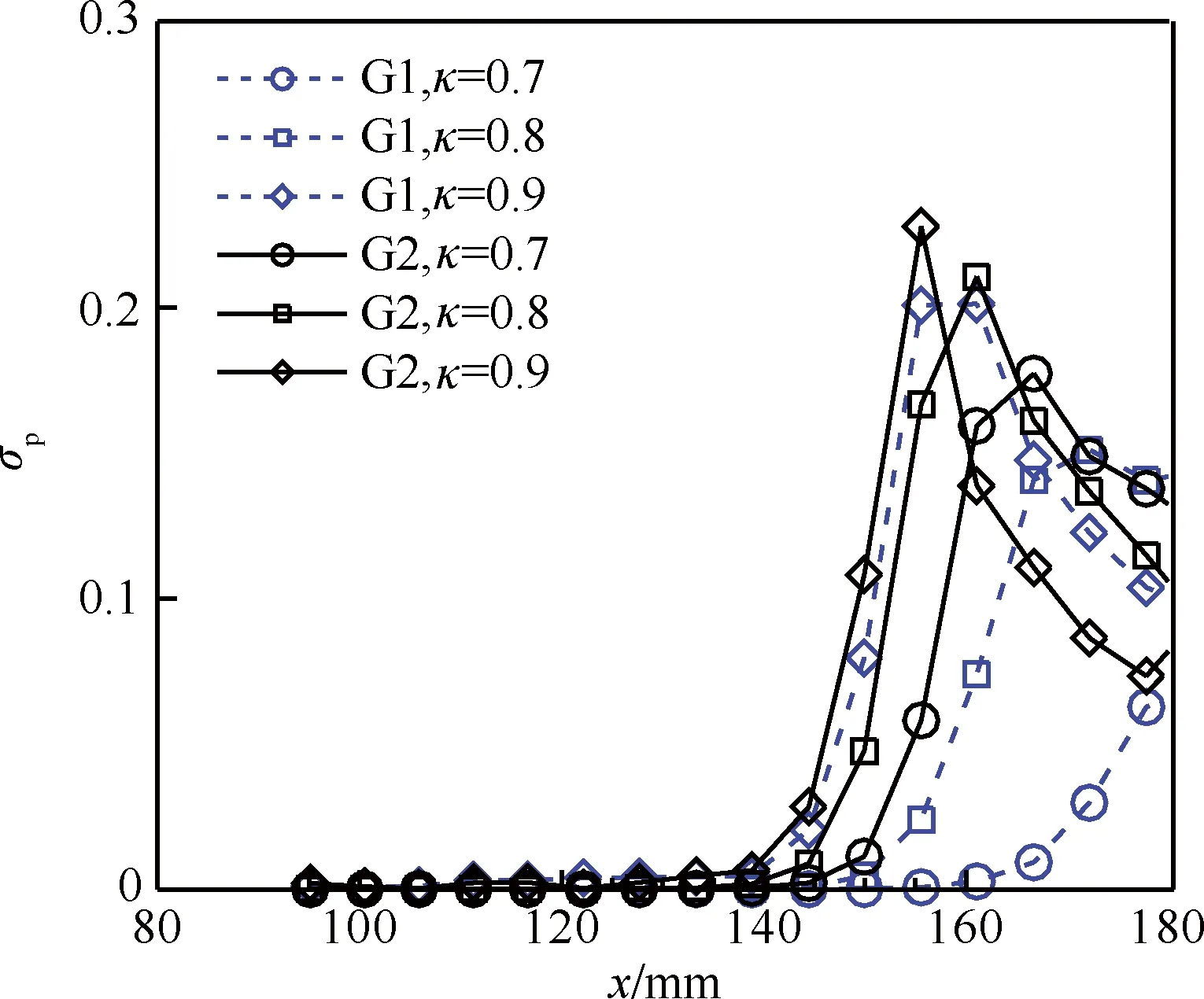
图9　沿流向涡压力脉动的均方根Fig.9　Root-mean-square of pressure fluctuations along a stream-wise vortex

4　结　论

1) 涡流发生器强制转捩过程的物理图像可以描述为：涡流发生器在其下游产生一对流向涡，这对流向涡失稳产生一系列“发卡”涡并逐渐演化直至破碎，最终使边界层转捩为湍流。

2) 涡流发生器下游流向涡的失稳包括两种模式：偶模式和奇模式，前者产生对称形式的涡破碎，后者产生弯曲形式的涡对破碎。本文开展的数值模拟研究同时捕捉到了这两种失稳模式。

3) 采用隐式大涡模拟方法计算强制转捩问题时，数值耗散对计算结果有明显影响，文中对网格和数值耗散影响作了测试：在较小的格式耗散情况下，计算更容易达到网格收敛；随着网格加密、耗散变小，计算得到的流向涡对破碎前移并趋于不变。

[1]BERRY S A, DARYABEIGI K, WURSTER K. Boundary-layer transition on X-43A[J]. Journal of Spacecraft and Rockets, 2010, 47(6): 922-934.

[2]KLEBANOFF P S, TIDSTROM K D. Mechanism by which a two-dimensional roughness element induces boundary-layer transition[J]. Physics of Fluids, 1972, 15(7): 1173-1188.

[3]RESHOTKO E, TUMIN A. Role of transient growth in roughness-induced transition[J]. AIAA Journal, 2004, 42(4): 766-770.

[4]SESCU A, PENDYALAY R K, THOMPSON D. On the growth of Görtler vortices excited by distributed roughness elements: AIAA-2014-2885[R]. Reston： AIAA, 2014.

[5]LI F, MALIK M R. Fundamental and subharmonic secondary instabilities of Görtler vortices[J]. Journal of Fluid Mechanics, 1995, 297: 77-100.

[6]LI F, CHOUDHARI M, CHANG C L, et al. Development and breakdown of Görtler vortices in high speed boundary layers: AIAA-2010-705[R]. Reston: AIAA, 2010.

[7]TULLIO N D, PAREDES P, SANDHAM N D, et al. Laminar-turbulent transition induced by a discrete roughness element in a supersonic boundary layer[J]. Journal of Fluid Mechanics, 2013, 735: 613-646.

[8]BERRY S A, HORVATH T J. Discrete-roughness transition for hypersonic flight vehicles[J]. Journal of Spacecraft and Rockets, 2008, 45(2): 216-227.

[9]BERRY S A, AUSLENDER A H, DILLEY A D, et al. Hypersonic boundary layer trip development for Hyper-X[J]. Journal of Spacecraft and Rockets, 2001, 38(6): 853-864.

[10]BERRY S A, NOWAK R J, HORVATH T J. Boundary layer control for hypersonic airbreathing vehicles: AIAA-2004-2246[R]. Reston: AIAA, 2004.

[11]赵慧勇, 周瑜, 倪鸿礼, 等. 高超声速进气道边界层强迫转捩试验[J]. 实验流体力学, 2012, 26(1): 1-6.

ZHAO H Y, ZHOU Y, NI H L, et al. Test of forced boundary-layer transition on hypersonic inlet[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(1): 1-6 (in Chinese).

[12]DANEHY P M, BATHEL B, IVEY C, et al. NO PLIF study of hypersonic transition over a discrete hemispherical roughness element: AIAA-2009-0394[R]. Reston: AIAA, 2009.

[13]冈敦殿, 易仕和, 陈植, 等. 超声速平板上直立圆台突起物绕流流场研究[C]//中国力学大会-2013. 北京: 中国力学学会, 2013.

GANG D D, YI S H, CHEN Z, et al. Flow field investigations of supersonic flow over a circular protuberance mounted on a flat plate[C]//CCTAM-2013. Beijing： The Chinese Society of Theoretical and Applied Mechanics, 2013 (in Chinese).

[14]张庆虎. 超声速流动分离及其控制的试验研究[D]. 长沙: 国防科学技术大学, 2013.

ZHANG Q H. Experimental investigation of supersonic flow separation and its micro-ramp control[D]. Changsha: National University of Defense Technology, 2013 (in Chinese).

[15]BORG M P, SCHNEIDER S P. Effect of freestream noise on roughness-induced transition for the X-51A forebody[J]. Journal of Spacecraft and Rockets, 2008, 45(6): 1106-1116.

[16]邓小兵. 来流噪声对高超声速进气道强制转捩的影响[C]//中国力学大会-2013. 北京： 中国力学学会， 2013.

DENG X B. Freestream noise impact on forced transition of hypersonic boundary layer[C]//CCTAM-2013. Beijing： The Chinese Society of Theoretical and Applied Mechanics, 2013 (in Chinese).

[17]MARXEN O, IACCARINO G, SHAQFEH E S G. Numerical simulations of hypersonic boundary-layer instability with localized roughness： AIAA-2011-0567[R]. Reston: AIAA, 2011.

[18]IYER P S, MUPPIDI S, MAHESH K. Roughness-induced transition in high speed flows: AIAA-2011-0566[R]. Reston: AIAA, 2011.

[19]DUAN Z W, XIAO Z X, FU S. Direct numerical simulation of hypersonic transition induced by ramp roughness elements: AIAA-2014-2037[R]. Reston: AIAA, 2014.

[20]DUAN Z W, XIAO Z X. Direct numerical simulation of geometrical parameter effects on the hypersonic ramp-induced transition: AIAA-2014-2495[R]. Reston: AIAA, 2014.

[21]涂国华, 燕振国, 赵晓慧, 等. SA和SST湍流模型对高超声速边界层强制转捩的适应性[J]. 航空学报, 2015, 36(5)： 1471-1479.

TU G H, YAN Z G, ZHAO X H, et al. SA and SST turbulence models for hypersonic forced boundary layer transition[J]. Acta Aeronautica et Astronautia Sinica, 2015, 36(5): 1471-1479 (in Chinese).

[22]周玲， 闫超， 孔维萱. 高超声速飞行器前体边界层强制转捩数值模拟[J]. 航空学报, 2014, 35(6): 1487-1495.

ZHOU L, YAN C, KONG W X. Numerical simulation of forced boundary layer transition on hypersonic vehicle forebody[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(6): 1487-1495 (in Chinese).

[23]周玲, 闫超, 郝子辉, 等. 转捩模式与转捩准则预测高超声速边界层流动[J]. 航空学报, 2016, 37(4): 1092-1102.

ZHOU L, YAN C, HAO Z H, et al. Transition model and transition criteria for hypersonic boundary layer flow[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(4): 1092-1102 (in Chinese).

[24]SAYADI T, MOIN P. Large eddy simulation of controlled transition to turbulence[J]. Physics of Fluids, 2012, 24(11): 923-938.

[25]ORLIK E, FEDIOUN I. Hypersonic boundary-layer transition forced by wall injection: A numerical study[J]. Journal of Spacecraft and Rockets, 2014, 51(4): 1306-1318.

[26]邓小兵, 金玲. 让误差飞一会儿——湍流大涡模拟中的动态自适应迎风方法[C]//中国力学大会-2013. 北京： 中国力学学会, 2013.

DENG X B, JIN L. Let the error fly for a while—A dynamic adaptive upwind method for large eddy simulations of turbulent flow[C]//CCTAM-2013. Beijing： The Chinese Society of Theoretical and Applied Mechanics, 2013 (in Chinese).

[27]朱自强, 吴子牛, 李津, 等. 应用计算流体力学[M]. 北京: 北京航空航天大学出版社, 1998： 54-88.

ZHU Z Q, WU Z N, LI J, et al. Application of computational fluid dynamics[M]. Beijing: Beihang University Press, 1998： 54-88 (in Chinese).

[28]JAMESON A. Time dependent calculations using multigrid with application to unsteady flows past airfoils and wings： AIAA-1991-1596[R]. Reston: AIAA, 1991.

[29]YOON S, JAMESON A. Lower-upper symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations[J]. AIAA Journal, 1988, 26(9): 1025-1026.

[30]DUAN L, BEEKMAN I, MARTN M P. Direct numerical simulation of hypersonic turbulent boundary layers with varying freestream Mach number： AIAA-2010-0353[R]. Reston: AIAA, 2010.

[31]LUND T S, WU X, SQUIRES K D. Generation of turbulent inflow data for spatially-developing boundary layer simulations[J]. Journal of Computational Physics, 1998, 140(2): 233-258.

[32]EDWARDS J R, CHOI J, BOLES J A. Hybrid LES/RANS simulation of a mach 5 compression-corner interaction: AIAA-2008-0718[R]. Reston: AIAA, 2008.

[33]SHUR M L, SPALART P R, STRELETS M K, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649

[34]SPALART P R, ALLMARAS S R. A one-equation turbulence model for aerodynamic flows： AIAA-1992-0439[R]. Reston: AIAA, 1992.

[35]GEORGIADIS N J, RIZZETTA D P, FUREBY C. Large-eddy simulation: current capabilities, recommended practices, and future research[J]. AIAA Journal, 2010, 48(8): 1772-1784.

赵晓慧男， 博士研究生， 助理研究员。主要研究方向： 湍流数值模拟， 高超声速空气动力学。

Tel.: 0816-2463219

E-mail: xhzhao@skla.cardc.cn

邓小兵男， 博士， 副研究员。主要研究方向： 计算流体力学， 湍流数值模拟。

Tel.: 0816-2463219

E-mail: xbdeng@skla.cardc.cn

毛枚良男， 博士， 研究员， 博士生导师。主要研究方向： 计算流体力学， 高阶精度格式， 高超声速空气动力学。

Tel.: 0816-2463296

E-mail: mm1219@163.com

Large eddy simulation for forced transition flow at hypersonic inlet

ZHAO Xiaohui1, DENG Xiaobing1,*, MAO Meiliang2, YANG Wei1, ZHAO Huiyong3

1. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center,Mianyang621000, China 2. Computational Aerodynamics Institute, China Aerodynamics Research and Development Center,Mianyang621000, China 3. Science and Technology on Scramjet Laboratory, China Aerodynamics Research and Development Center,Mianyang 621000, China

Forced transition is commonly used for a hypersonic air breathing vehicle to ensure its scramjet’s normal start by placing roughness elements or vortex generators in the inlet boundary layer. To get a clear image of forced transition process, an implicit large eddy simulation method is used for laminar-turbulent forced transition flows in the boundary layer of a hypersonic inlet configuration. Main structures are obtained for the forced transition flows induced by the vortex generators shaped of diamonds and ramps, which show that the flows are dominated by stream-wise counter-rotating vortices. Fluctuations grow in the stream-wise direction and cause instabilities. Two fundamental modes of the instabilities are found in the simulations, the even mode and the odd one. The even mode leads to a varicose way of breaking down of the counter-rotating vortices, while the odd one leads to a sinuous way. Strings of hairpin vortices are generated after the breaking down and finally cause the transition. A discussion is carried out on the computation convergence together with the influence of the grids and numerical dissipation.

hypersonic; inlet; forced transition; vortex generator; large eddy simulation

2016-02-16； Revised： 2016-02-17； Accepted： 2016-06-21； Published online： 2016-06-2715:34

National Natural Science Foundation of China (11402289)

. Tel.： 0816-2463219E-mail: xbdeng@skla.cardc.cn

2016-02-16； 退修日期： 2016-02-17； 录用日期： 2016-06-21；

时间： 2016-06-2715:34

www.cnki.net/kcms/detail/11.1929.V.20160627.1534.008.html

国家自然科学基金 (11402289)

.Tel.： 0816-2463219E-mail: xbdeng@skla.cardc.cn

10.7527/S1000-6893.2016.0200

V211.3; O355

A

1000-6893(2016)08-2445-09

引用格式： 赵晓慧， 邓小兵， 毛枚良， 等． 高超声速进气道强制转捩流动的大涡模拟[J]． 航空学报, 2016, 37(8): 2445-2453. ZHAO X H, DENG X B, MAO M L, et al. Large eddy simulation for forced transition flow at hypersonic inlet[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2445-2453.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160627.1534.008.html