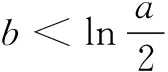变更与甄选主元
刘 冰
(黑龙江省哈尔滨师范大学附属中学,150080)
变更与甄选主元
刘冰
(黑龙江省哈尔滨师范大学附属中学,150080)
主元法,是指在含有两个或两个以上变元的问题的解决过程中,选择其中一个变元作为研究的主要对象,视为主元,而将其余各变元视为参数或常量的一种思想方法.主元法将问题转化为关于该主元的式子、方程或函数,可将问题难度大大降低,使问题获得巧解,化难为易.在多变量问题的解题中,一旦选对了主元,等于在战斗中选择了正确的方向.
笔者认为高考中主元法的应用主要分为以下两种:变更主元法与甄选主元法.
一、变更主元法——巧解含参问题
含参问题是高考的必考题型.主元法是处理多元问题的一种重要方法.当参数与主元存在确定函数关系时,变更主元不失为降低问题处理难度的有效途径.
例1(2016年全国高考题)
解(1)f(x)的定义域为
(-∞,-2)∪(-2,+∞).
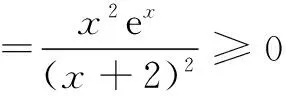
当且仅当x=0时,f ′(x)=0,所以f(x)在(-∞,-2),(-2,+∞)单调递增.
因此,当x∈(0,+∞)时,
f(x)>f(0)=-1,
所以(x-2)ex>-(x+2),
即(x-2)ex+x+2>0.
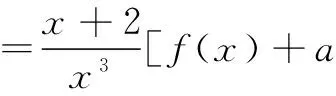
由(1)知,f(x)+a单调递增,对任意a∈[0,1),有
①
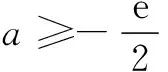
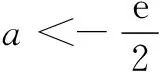
当0 当x>t时,f(x)+a>0,有g′(x)>0,g(x)单调递增. 将①代入,得 其中t∈(0,2]. 例2(2016年全国高考题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点. (1)求a的取值范围; (2)设x1,x2是f(x)的两个零点,证明: x1+x2<2. 解(1)f ′(x)=(x-1)ex+2a(x-1) =(x-1)(ex+2a). (i)若a=0,则f(x)=(x-2)ex,f(x)只有一个零点. (iii)若a<0,由f ′(x)=0,得x=1或x=ln(-2a). 综上,a的取值范围为(0,+∞). (2)不妨设x1 由(1)知,x1∈(-∞,1),x2∈(1,+∞),2-x2∈(-∞,1).又因f(x)在(-∞,1)内单调递减,所以x1+x2<2,即f(x1)>f(2-x2),即证f(2-x2)<0. 因为f(2-x2)=-x2e2-x2+a(x2-1)2, 又f(x2)=(x2-2)ex2+a(x2-1)2=0, 故f(2-x2)==-x2e2-x2-(x2-2)ex2, x2∈(1,+∞). 设g(x)=-xe2-x-(x-2)ex,x∈(1,+∞),则g′(x)=(x-1)(e2-x-ex). 当x>1时,g′(x)<0,而g(1)=0,故当x>1时,g(x)<0,从而g(x2)=f(2-x2)<0,故x1+x2<2. 评注问题(2)中x1,x2没有相互约束关系,要注意问题的串联,借助第(1)问的结论来证明.由单调性可知x1+x2<2等价于f(x1)>f(2-x2),由此甄选主元x2,即证f(2-x2)<0,实现二元问题化归为一元问题,利用函数思想加以解决,降低试题难度.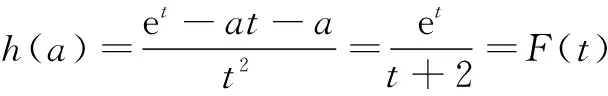
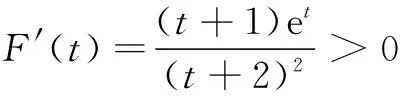
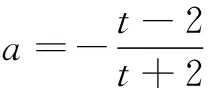
二、甄选主元法——巧解多元问题