巧用导数几何意义 破解参数取值范围

金　莹

(广东省佛山市南海中学，528211)



○学习指导○

巧用导数几何意义破解参数取值范围

金莹

(广东省佛山市南海中学，528211)

求参数的取值范围是一类活跃在高考导数题中的热点问题,求解策略一般有三种:(1)分离参数法;(2)分类讨论法;(3)数形结合法，例如转化成两个函数图象的交点个数问题．第一种方法是常规思路,一旦遇上求导后极为复杂,或者要借用大学的洛必达法则等超纲知识,就会思维受阻．第二种方法往往难度较大,要排除反面情况,学生不易掌握．第三种方法如一缕清风拂面,瞬间吹散了百转千回的迷雾．本文结合第三种方法,例说巧用导数几何意义,破解一类参数取值范围问题．

例1(2010年海南高考题)设函数f(x)=x(ex-1)-ax2.

(2)若当x≥0时f(x)≥0,求a的取值范围．

参考答案给出的方法是分类讨论,f(x)=x(ex-1-ax)．令g(x)=ex-1-ax,则g′(x)=ex-a．① 若a≤1,则当x∈(0,+∞)时,g′(x)>0,g(x)为增函数,而g(0)=0,从而当x≥0时g(x)≥0,即f(x)≥0.

② 若a>1,则当x∈(0,ln a)时,g′(x)<0,g(x)为减函数,而g(0)=0,从而当x∈(0,ln a)时g(x)<0,即f(x)<0.综合得a的

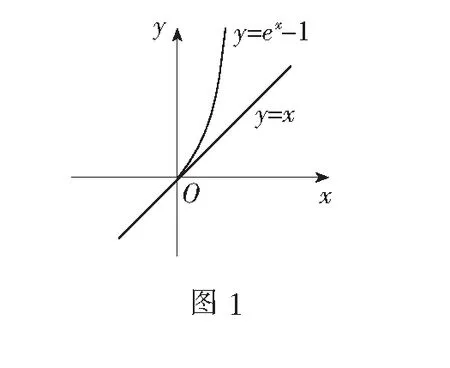
解我们将问题转化为ax≤ex-1在[0,+∞)上恒成立,分别画出它们的图象(如图1),y=ex-1在原点处的切线方程为y=x．

当x∈[0,+∞)时要使过原点的直线y=ax恒在曲线y=ex-1下方,当且仅当直线y=ax的斜率小于等于切线斜率1时才满足题意,故易知a≤1．

例2(2013年全国高考题)已知函数f(x)=x2+ax+b,g(x)=ex(cx+d).若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2．

(1)求a,b,c,d的值；

(2)若x≥-2时，f(x)≤kg(x)，求k的取值范围.

解法1(参考答案)(1)a=4,b=2,c=2,d=2(过程略).

(2)由(1)知，f(x)=x2+4x+2,g(x)=2ex(x+1).设函数F(x)=kg(x)-f(x)=2kex(x+1)-x2-4x-2(x≥-2),则F′(x)=2kex(x+2)-2x-4=2(x+2)(kex-1).由题设，可得F(0)≥0,即k≥1,

令F′(x)=0,得x1=-ln k,x2=-2,接下来对两根的大小进行分类讨论：

(1)若1≤k0,即F(x)在(-2,x1)单调递减，在(x1,+∞)单调递增，故F(x)在x=x1取最小值F(x1).而F(x1)=2x1+2-x21-4x1-2=-x1(x1+2)≥0,∴当x≥-2时，F(x)≥0,即f(x)≤kg(x)恒成立.

(2)若k=e2,则F′(x)=2e2(x+2)(ex-e-2),∴当x≥-2时，F′(x)≥0,∴F(x)在(-2,+∞)单调递增，而F(-2)=0,∴当x≥-2时，F(x)≥0，即f(x)≤kg(x)恒成立.

(3)若k>e2,则F(-2)=-2ke-2+2=-2e-2(k-e2)<0,∴当x≥-2时，f(x)≤kg(x)不可能恒成立.

综上所述，k的取值范围为[1,e2].

分类讨论的解法思维量和计算量都很大,大多数学生不易掌握．如果本题用数形结合的方法,巧用切线求参数k的取值范围,会简捷很多,且直观的图形思维学生更易理解．

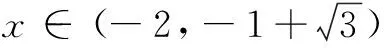
x→+∞时,h(x)=→0.而φ(x)=2k(x+1)过定点(-1,0),如图2.

当φ(x)与h(x)相切时,求出斜率,从而求出k的范围．

过点P(-1,0)向h(x)作两条切线,设切点为(x0,y0)，则

解得x0=0或x0=-2.

(1)当k≤0时,求函数f(x)的单调区间;

(2)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围．

解参考答案是分类讨论，从略.以下考虑用数形结合法，转化为图象的交点个数.

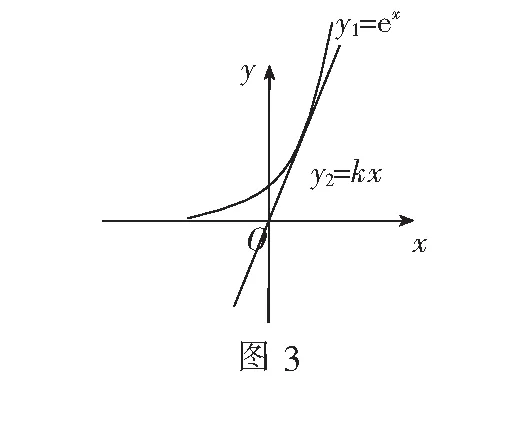
记y1=ex,y2=kx,也就是它们的图象在(0,2)内有两个交点(如图3).

易求得切点为(1,e),切线斜率k=e．

巧用导数的几何意义破解参数范围问题,还可以用在证明题中．比如,2014年的新课标Ⅱ全国高考题文科第21题,参考答案的方法进行了分类讨论和巧妙的放缩,这对于文科生有些困难．但如果利用图象,抓住临界位置“切线”,就可以形象地证明它们的图象只有一个交点．

例4(2014年全国高考题)已知函数f(x)=x3-3x2+ax+2,曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为-2.

(1)求a;

(2)证明:当k<1时,曲线y=f(x)与直线y=kx-2只有一个交点.

(参考答案中的解法略)

简解(1)a=1(过程略).

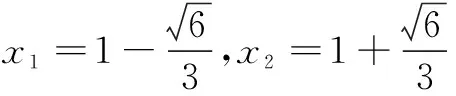
由y=f(x)的简图(如图4),直线y=kx-2过定点(0,-2).

当直线y=kx-2与曲线y=f(x)相切时,设切点(x0,y0)，则

∴x0=2,切点为(2,0).

此时切线斜率k=1,当动直线y=kx-2绕定点(0,-2)从切线位置顺时针旋转到y轴时,它们的图象都只有一个交点，故k<1．

通过以上几道高考题,我们可以总结出这类参数范围问题的通法:将函数式进行变形,一边化为直线型,转化为两图象的交点个数问题．往往相切时是临界位置,所以，能够准确熟练地求切线的斜率是解决问题的基础．利用导数的几何意义为切线斜率,可以秒杀一类参数取值范围问题,数形结合,化抽象为直观、变繁琐为简捷，在高考导数题中常能起到四两拨千斤的作用．