数学课的美:层层递进
安徽省合肥市海顿学校
刘昌福 (邮编:230051)
教学参考
数学课的美:层层递进
安徽省合肥市海顿学校
刘昌福(邮编:230051)
说到美,大家会认为跟数学课挨不上边,其实这是一个误区,数学课有她独特之美,如严谨之美,对称之美,对应之美,等等.笔者在这里只说一种数学课之美——层层递进,且以一次青年教师课堂教学评比为例展开,这次评比的课题是:沪科版教材八年级上册第13章《三角形中的边角关系、命题与证明》第2节《命题与证明》中的一节课《三角形内角和定理及其推论》.
1 动手操作获取解题思路,实现从小学到初中的递进(第一次递进)
众所周知,孩子们在小学阶段已学过三角形内角和等于180°,他们当时探究的方法是通过动手操作去剪拼或折叠而得.我们知道在数学学科里,动手操作也是学习数学的一个重要方法,这是对数学学习方法很好的补充.对传统的数学学习的理解是:学习数学,就是计算、证明,传统的教学也是“交通警察各管一段”,根本不考虑什么衔接问题.新课改以来,明确提出,学习数学不仅有传统的计算、证明,还有归纳、猜想、动手操作等方法.同时也明确指出,教学是为了培养孩子们终身学习的能力.先将初小衔接放在一边,只说这节课涉及的动手操作问题.动手操作,很多老师都做了,但很多老师在课堂上会忽略非常重要的一点,动手操作除了是数学学习的一个重要方法,还可以通过动手操作获得数学活动经验,有了数学活动经验,可以帮助我们找到解决问题的思路.这正是新课标中将“双基”(基础知识、基本技能)修订为“四基”( 基础知识、基本技能、基本数学活动经验和基本的数学思想方法)的原因.就本节课而言,回顾小学通过折叠、剪拼等操作方法探究三角形内角和等于180°,可以积累出“在一个顶点处拼接出一个平角”这个数学活动经验,从而找到证明三角形内角和等于180°的方法.这就是教材为什么一开始安排添加辅助线是“延长BC到点D,过点C以CD为一边作∠DCE=∠B”,而不是以前的“延长BC到点D,过点C作CE∥AB”(如图(1))的原因, 其实这就是从小学到初中的递进.
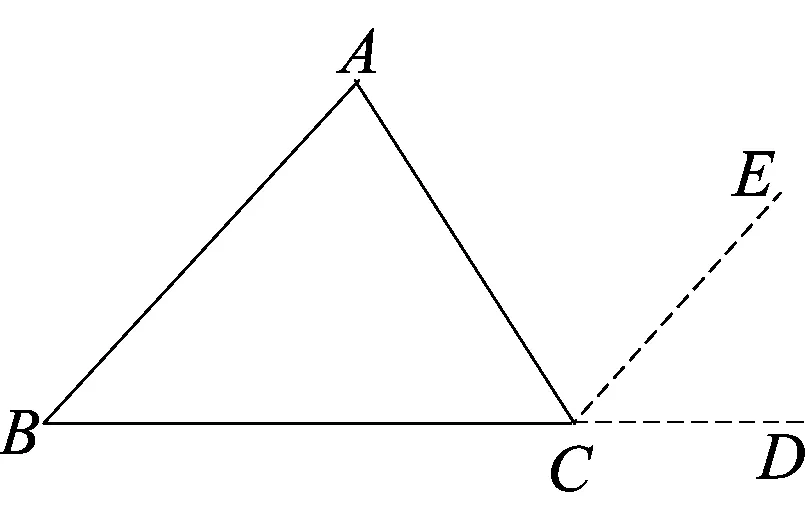
图1
具体为:如图1,延长BC到点D,过点C以CD为一边作∠DCE=∠B, 可得CE∥AB,从而完成将∠A、∠B、∠C成功地移至以C为顶点的平角∠BCD,命题得证.
遗憾的是很多老师的课堂没有意识到这种操作和添辅助线之间的联系,将二者完全割裂,纯粹为了解题而解题,舍弃了通过动手操作积累数学活动经验,从而获取解题思路这个好过程,没有实现从小学到初中的递进,实在可惜!因此,我得再补充一句:《课程标准》应作为我们老师的床头工具书,遇到某个教学问题时应随时翻看查阅,做到教学实践与《课程标准》紧密联系,而不只是形式主义的组织集体学习.
2 由平行线产生联想,实现第二次递进
接着刚才的课,教师继续引导:通过“延长BC到点D,过点C以CD为一边作∠DCE=∠B, 可得CE∥AB”的启发,可以发现:作平行线可以完成角的移动,可以将△ABC的三个内角移至过同一个点的平角.受此启发,引导学生继续探究证明三角形内角和定理的其它方法.学生自然可以探究出过某一点作一边的平行线,从而得到证明三角形内角和等于180°的很多方法,如图2、图3所示等(详解略).实现本节课的第二次递进.

图2
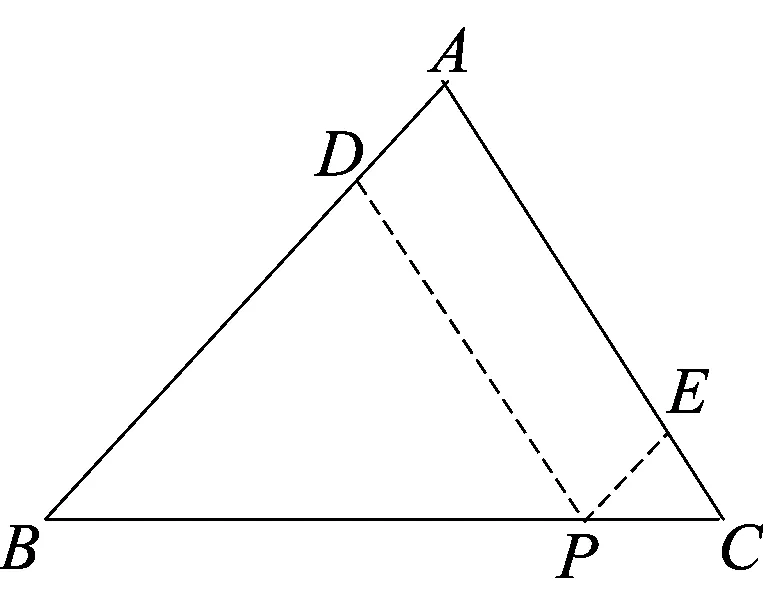
图3
3 由180°产生联想,实现第三次递进
这节课继续进行.教师再引导:对于命题中的180°,除了平角可以得到,还学过哪些知识可以得到180°呢?启发学生通过“两直线平行,同旁内角互补”及两直角之和等于180°,再探究出新的证明方法.很多同学能探究出可以通过“两直线平行,同旁内角互补”得到180°,或两个直角之和等于180°,于是有了4、图5等解法(详解略),实现本节课第三次递进上升.

图4

图5
4 及时总结归纳,实现第四次递进
有了刚才的探究过程,教师启发学生思考并总结归纳:这些方法的本质就是为了实现两个方面:(1)如何在图形中巧妙实现“∠A+∠B+∠C”,即将∠A、∠B、∠C移至某一共同顶点处;(2)如何在图形中得到180°.两个方面都实现了,解题就成了很自然的事.因此证明方法还有很多,同学们课后可以继续探究.其实这就是实现了第四次递进.可惜的是我们很多年轻的同行们,只是为了实现证明方法多样化,其实真是舍本求末了.这里我还要嘱咐一句:数学课及时总结归纳,可以完成已学知识与“上位知识”和“下位知识”的联系(上位知识”和“下位知识”详见章建跃《促进数学理解的教学策略》或笔者的论文《数学理解系统化策略教学的实践与思考》),实现数学知识的系统化.
5 善于捕捉数学本质问题,实现第五次递进
抓住图4证法中的本质东西,可以实现第五次递进.我们先来分析图4证法中的本质东西在哪里?如图4,过点A作AD∥BC,可得∠BAD+∠B=180°,本质东西就在等式“∠BAD+∠B=180°”与结论中的等式“∠A+∠B+∠C=180°”的比较,引导学生注意在等式变形中要保留等式“∠BAD+∠B=180°”中的∠B和180°,因为这是结论“∠A+∠B+∠C=180°”已经含有的项,而要替换的是“∠BAD”(因为结论中没有∠BAD这一项),引导学生这样思考问题才是将来数学学习中最为本质的东西,应早点渗透.其实就实现第五次递进.可惜的是我们的老师更多的只是轻描淡写地给出证明过程,没有足够的让学生体会和感悟其中的数学变换的本质方法.
6 课堂兼顾应试,实现第六次递进
大家都说:“没有分数就没有今天,光有分数没有明天”.对于初中数学教学,在提高学生数学能力的同时,还应决胜中考,这一点不容回避.也就是说如果平时教学扎实,取得中考高分其实是很自然的事.比如以上所说,如果平时教学善于捕捉数学本质问题,三年的数学课堂一直坚持这样的教学,取得高分一定不是问题.当然我们在备课中一定还要考虑学生将来的数学学习最需要什么,除了像刚才那样不断渗透本质的方法以外,还应该直接安排重要的数学知识进课堂.如这节课中其中一位老师安排了这样一个练习,笔者就比较欣赏.

图6
如图6,在△ABC中,∠ACB=90°,CD⊥AB于D,求证:∠ACD=∠B.
学生完成后,再追问,图中还有其它相等的角吗(直角除外)?
我为什么欣赏此题?教学经验丰富的老师一定知道,对于这个图形的研究在初中阶段尤为重要,如在相似形一节中,我们会经常和图6打交道,此时渗透,就像棋局高手随手丢下一颗“闲子”,最后在绞杀决胜中起到奇兵的作用.高明的棋手是这样,高水平的教学也是这样.
其实,我们课堂上安排例题或学生练习,本身也应该遵循层层递进、螺旋上升这个原则.可总结如下:直接运用知识,模仿似的例题是最低层次的要求;能和已学知识联系,新知联系旧知,是较高层次的要求;如果还能灵活运用所学新知,解决实际问题,那就是更高层次的要求了.
坚持这样教学,中考考出好成绩真的就成为我们教学的副产品,也不需要再刻意去通过加重学生学业负担去实现.这不仅是本节课的第六次递进,更是实现“轻负高效”的好方法.
层层递进,只是数学美之一,因为这节课的这个美点非常明显,所以认真分析了这个方面,其实数学课的美还有很多.总之,我们真的要认真琢磨每一节课,让每一节课都体现出更多的数学之美来.用数学之美去吸引孩子们的眼球,而不是硬性要求.
2016-07-12)

