一道“异题”的求解与变式
2016-11-10 00:30江苏省南京金陵中学河西分校
中学数学教学 2016年5期
江苏省南京金陵中学河西分校
李玉荣 (邮编:210019)
一道“异题”的求解与变式
江苏省南京金陵中学河西分校
李玉荣(邮编:210019)
近日,有网友在中学数学杂志群里晒出了这样一道题:
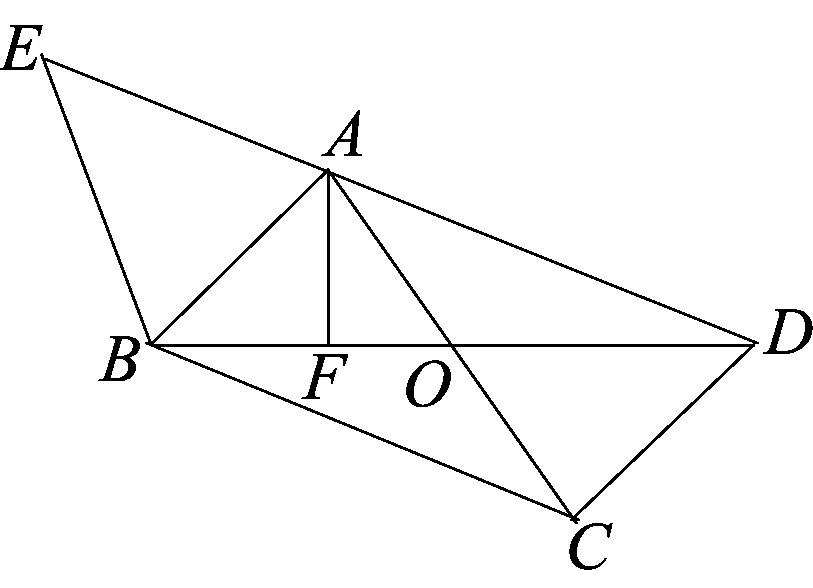
图1
此题被网友戏称为不知道怎么设计出来的“异题”:
一是题目给出的条件过于复杂,即使经过化简也不能确定角的度数,如果一味地想求出角,求解走入死胡同;二是怎样将所得角的关系转化为边的关系?求解的过程步履维艰.笔者并不赞同在数学试卷中这样命制填空题,但对如何由AB=5求解FO颇感兴趣,悉心研究,收获不小,撰文与大家分享.
1 求解

图2
思路1取斜边中点,利用“直角三角形斜边上的中线等于斜边的一半”求解
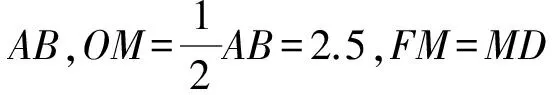
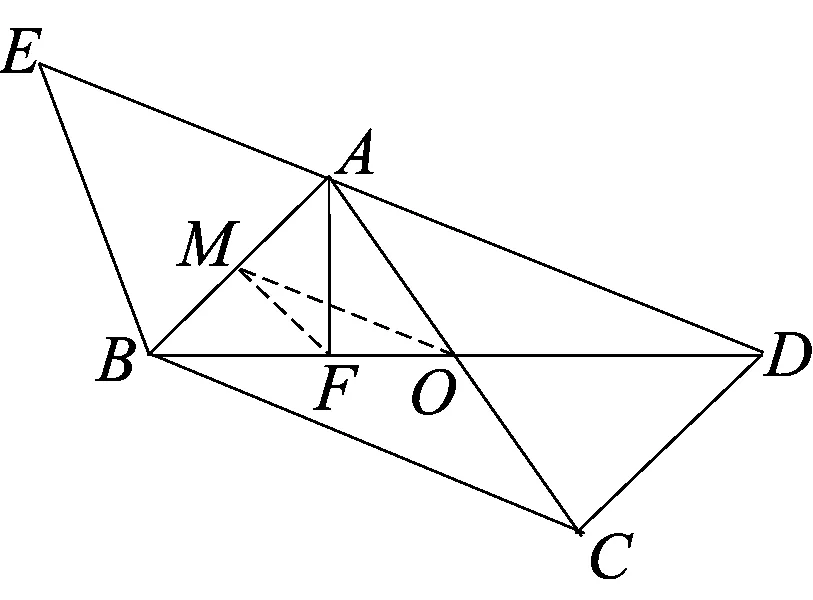
图3

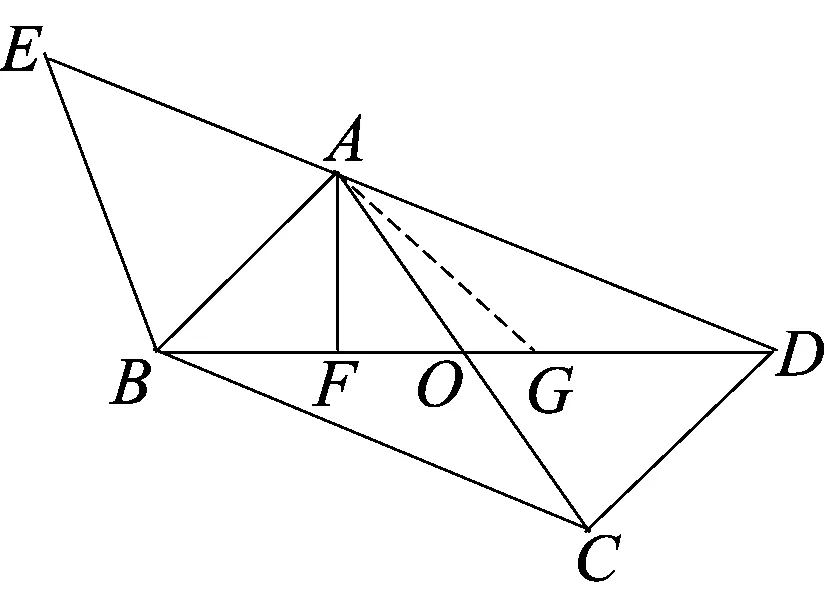
图4
思路2构造等腰三角形,利用“等腰三角形三线合一”求解
解法3如图4,在BD上取点G使得DG=AG,则∠GAD=∠ADB=x,从而∠AGB=2x=∠ABG,所以DG=AG=AB=5,BF=FG,
即BO-FO=FO+OD-DG,
因为BO=DO,
所以2FO=DG=5,故FO=2.5.

图5
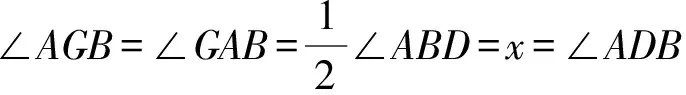
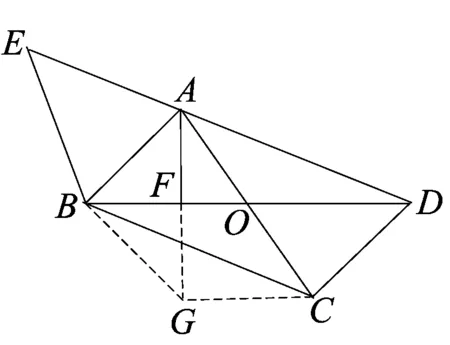
图6
思路3构造三角形中位线,利用“三角形中位线定理”求解

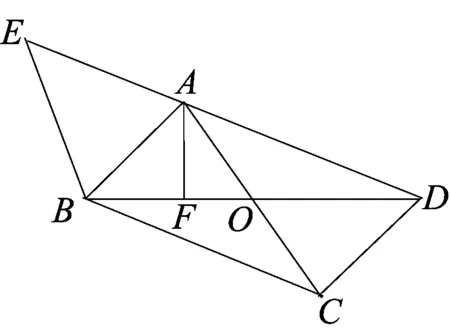
图7
思路4利用三角函数直接求解
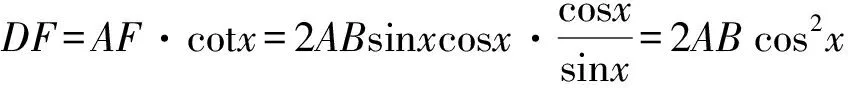
2 变式
此“异题”的条件可直接弱化,得到下面两道
“贴近学生最近发展区”的适宜题目:

图8

图9
题2如图9,在△ABC中,∠ABC=2∠ACB,AO为中线,过点A作AF⊥BD于点F,若AB=5,则FO的长为______.
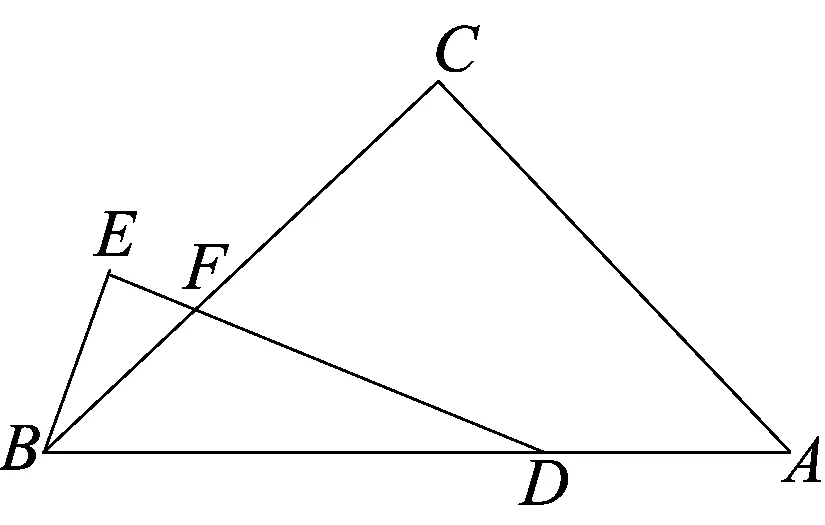
图10
3 类比
笛卡尔曾说过:我所解决的每一个问题都将成为一个范例,以用于解决其它的问题.聪明的读者,你能用几种方法解决下面这道题?
2016-08-06)
猜你喜欢
华夏教师(2021年28期)2021-05-23
华夏教师(2021年28期)2021-05-23
中学生数理化·七年级数学人教版(2020年10期)2020-11-26
中学生数理化·七年级数学人教版(2020年10期)2020-11-26
初中生学习指导·提升版(2020年6期)2020-09-10
语数外学习·初中版(2020年5期)2020-09-10
黄埔(2020年4期)2020-08-13
黄埔(2020年4期)2020-08-13
中学生数理化·七年级数学人教版(2019年4期)2019-05-20
中学生数理化·七年级数学人教版(2019年4期)2019-05-20

