圆锥曲线双切线一个等角性质的探究历程

湖北省阳新县高级中学

邹生书　　(邮编：435200)



圆锥曲线双切线一个等角性质的探究历程

湖北省阳新县高级中学

邹生书(邮编：435200)

圆锥曲线是高中数学的主干知识，是高考和数学竞赛的重点考查内容，主要考查运算求解、推理论证以及探究问题的能力.其中不少题目的结论可以推广到一般情形，甚至可以类比到其它类型的圆锥曲线，从而得出圆锥曲线统一的几何性质.这样结论具有拓展性的试题是研究性学习的好素材，倍受高中数学教师和数学爱好者的青睐，推广类比不亦乐乎.2016年内蒙古自治区高中数学联赛预赛第10题就是这样一道具有研究价值的试题，本文将对该题推广、类比的探究历程呈现给读者，供参考.

图1

题目如图1，已知双曲线x2-y2=2的左右焦点分别为F1、F2，过定点P(2,3)作曲线的切线，切点分别为A、B，且A点的横坐标小于B点的横坐标.(1)求直线AB的方程；(2)证明∠F1PA=∠F2PB．

1　一般化探究

一般性寓于特殊性之中，特殊情形往往会掩盖问题的本质.这里定点P的横坐标恰好与右焦点的横坐标相等，情况很特殊，那么，当点P为任意一点时，所证的两个角是否仍然相等呢?为了避免盲目计算，笔者利用现代信息技术，运用几何画板动态实验惊喜发现两角总是相等.推广后的一般性结论与证明如下.

图2

证明(注：在下面的证明中限于篇幅，我们只考虑点P在x轴上方的情形，点P在x轴下方时同理可证，这里省略)如图2，设P(x0,y0)，不妨设A点的横坐标小于B点的横坐标.当过点P的切线斜率存在时，设斜率为k，则切线方程为y-y0=k(x-x0)，即y=kx+y0-kx0，将其代入双曲线方程整理得

(a2k2-b2)x2+2a2k(y0-kx0)x+a2(y0-kx0)2+a2b2=0，

△=4a4k2(y0-kx0)2-4a2(a2k2-b2)[(y0-kx0)2+b2]=0，整理得

①

在过点P的4条直线PA、PB、PF1、PF2中至多有一条直线与x轴垂直，下面分三种情形进行讨论.

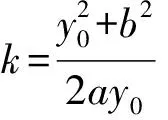
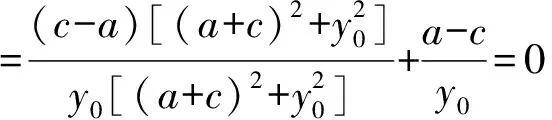
所以tan∠F1PA=tan∠F2PB，又∠F1PA,∠BPF2∈(0,π)，即∠F1PA=∠F2PB．

同理可证，当PA垂直于x轴时，∠F1PA=∠F2PB．

所以tan∠F1PA=tan∠F2PB，又∠F1PA、∠BPF2∈(0,π)，即∠F1PA=∠F2PB．

同理可证，当PF1垂直于x轴时，∠F1PA=∠F2PB．

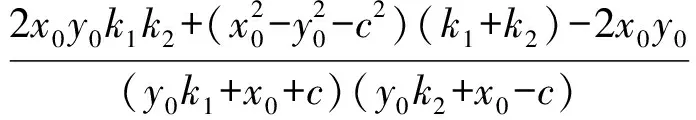
所以tan∠F1PA=tan∠F2PB，又∠F1PA,∠BPF2∈(0,π)，即∠F1PA=∠F2PB．

2　类比探究

类比是一种从特殊到特殊的合情推理，其正确性需要严格的逻辑证明.笔者通过几何画板研究发现上述双曲线切线的等角性质在椭圆中也成立.一般来说，若双曲线具有某种性质，则椭圆也具有类似的性质，其证明表述也大同小异，只须在将b2替换成-b2的同时，结合图形作些微调则可.椭圆切线的等角性质及证明如下：

图3

证明(注：在下面的证明中限于篇幅，我们只考虑点P在x轴上方的情形，点P在x轴下方时同理可证，这里省略)如图3，设P(x0,y0)，不妨设A点的横坐标小于B点的横坐标.当过点P的切线斜率存在时设斜率为k，则切线方程为

y-y0=k(x-x0)，即y=kx+y0-kx0，代入椭圆方程整理得

(a2k2+b2)x2+2a2k(y0-kx0)x+a2(y0-kx0)2-a2b2=0，

△=4a4k2(y0-kx0)2-4a2(b2+a2k2)[(y0-kx0)2-b2]=0，整理得

①.

在过点P的4条直线PA、PB、PF1、PF2中至多有一条直线与x轴垂直，下面分三种情形进行讨论.

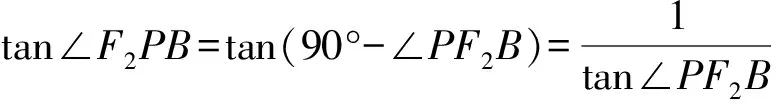
所以tan∠F1PA=tan∠F2PB，又∠F1PA,∠BPF2∈(0,π)，所以∠F1PA=∠F2PB．

同理可证，当PA垂直于x轴时，∠F1PA=∠F2PB．

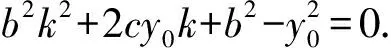
所以tan∠F1PA=tan∠F2PB，又∠F1PA,∠BPF2∈(0,π)，所以∠F1PA=∠F2PB．

同理可证，当PF1垂直于x轴时，∠F1PA=∠F2PB．

所以tan∠F1PA=tan∠F2PB，又∠F1PA,∠BPF2∈(0,π)，所以∠F1PA=∠F2PB．

3　“补美”探究

椭圆、双曲线都封闭曲线且有两个焦点，而抛物线是开放的曲线且只有一个焦点，而上述切线的性质都与两个焦点有关，是否断言抛物线就没有类似性质呢？如果是这样结论就不完美，能否将结论补充完美呢？“生活中的美无处不在，只是缺少发现美的眼睛”.“没有大胆的猜想，就做不出伟大的发现”.我们不妨来个大胆假设，把抛物线当作是在无穷远处相交的封闭曲线且有两个焦点，一个焦点是我们熟知F，另一个焦点设为H它在对称轴的无穷远处，则PH平行于对称轴，于是问题转化为∠FPA=∠HPB是否成立.笔者借助几何画板动态演示发现∠FPA=∠HPB成立.结论如下：

性质3已知抛物线y2=2px(p>0)的焦点为F，点A、B是抛物线上任意两点，若抛物线在点A、B处的切线相交于点P，过点P作PH平行于x轴，且点H在抛物线内部，则∠FPA=∠BPH．

证明从略.

4　完美结局

通过上述大胆假设小心论证的“补美”探究，我们得出了抛物线双切线的一个奇异的等角性质.至此，圆锥曲线的双切线的等角性质似乎就完美无缺了.其实不然，圆也是圆锥曲线大家庭中的重要一员，圆的切线我们有如下性质：过圆外一点向圆引两条切线，这一点与圆心的连线平分两切线的夹角.圆与椭圆关系密切，通过伸缩变换可以相互转化，我们可以把圆当作是两焦点重合于中心的特殊椭圆，当椭圆两个焦点重合时椭圆变成了圆，性质2中椭圆的切线性质就变成了圆的切线性质.可见，本文中椭圆、双曲线和抛物线双切线的等角性质可以看作是圆的双切线的等角性质在圆锥曲线中的类比拓展.至此，圆锥曲线双切线的等角性质可以画上一个圆满的句号.

在探究中发现美、创造美、欣赏美、体验美，提升审美能力和数学素养，探究性学习我们一直在路上.

1邹生书.例谈圆锥曲线双切线问题的处理方法[J].数理化学习，2012(11)

2冯克永.“基于补美”的数学教学[J].中学数学教学，2015(6)

2016-08-12)