模糊推理SIS算法的统一形式及其还原性*

李　骏，白莉君

兰州理工大学 理学院，兰州 730050

模糊推理SIS算法的统一形式及其还原性*

李骏+，白莉君

兰州理工大学 理学院，兰州 730050

模糊推理是模糊控制的核心问题，还原性则是评价模糊推理算法好坏的重要标准之一。在正则蕴涵算子的统一框架下，给出了基于模糊推理SIS（subsethood infer subsethood）算法的模糊取式（fuzzy modus ponens，FMP）问题解的统一表达式；基于SIS算法为模糊拒取式（fuzzy modus tollens，FMT）问题提出了一种改进的求解原则，并给出了FMT问题解的统一形式；证明了SIS FMP算法和SIS FMT算法均满足无条件还原性，讨论了FMP问题及FMT问题基于SIS算法的λ-水平解。该算法将为模糊控制领域提供更多可供选择的模糊推理方法。

模糊控制；模糊推理；正则蕴涵算子；SIS算法

1　引言

模糊推理是模糊控制的核心问题，模糊推理最基本的两种推理形式如下：

模糊取式（fuzzy modus ponens，FMP）：

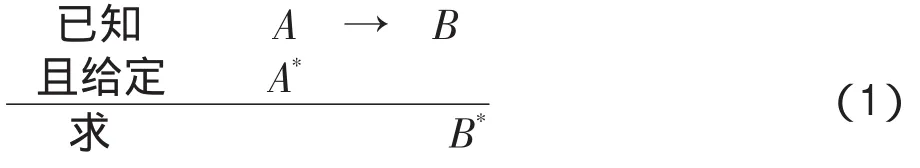
模糊拒取式（fuzzy modus tollens，FMT）：

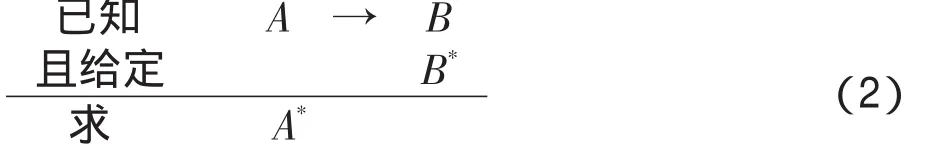
这里A,A*∈F(X)，B,B*∈F(Y)，F(X)、F(Y)分别表示非空论域X、Y上的全体模糊集。

1973年，美国控制论专家Zadeh提出了求解FMP问题的合成推理方法（compositional rule of inference，CRI）[1]。随后模糊界围绕CRI算法展开了比较深入的研究，在理论上和应用上取得了丰富的成果[2-4]。然而尽管CRI算法在计算上是简便的，但是它却缺乏严格的逻辑依据[5-6]。为了给模糊推理奠定严格的逻辑基础，王国俊教授提出了模糊推理的全蕴涵三I算法[5]。三I算法相较于CRI算法具有更好的逻辑背景，因此吸引了不少学者对其进行研究，并得到了大量研究成果。比如：文献[7-8]分别给出了基于正则蕴涵算子和剩余型蕴涵算子的三I算法的统一形式；文献[9]研究了基于反向支持度的三I算法；文献[10-14]基于不同度量研究了三I算法的鲁棒性。

另一方面，除了鲁棒性，算法的还原性也是评价模糊推理方法好坏的重要标准之一，尽管三I算法在还原性方面具有比CRI算法更好的性质，但它并不满足无条件还原性[5-8]。为此，文献[15]提出了一种新的模糊推理算法——SIS（subsethood infer subsethood）算法。

SIS FMP原则[15]FMP问题（1）的SIS解B*是使得下式：

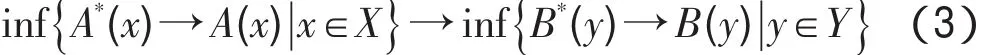
取最大值的F(Y)中的最大模糊集。

SIS FMT原则[15]FMT问题（2）的SIS解A*是使得下式：

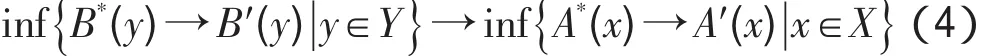
取最大值的F(X)中的最大模糊集。这里B′、A′分别是模糊集B、A的补集。

文献[15]在蕴涵算子分别取R0算子和Lukasiewicz算子的情形下证明了满足SIS FMP和SIS FMT原则的解均存在，并给出了求解算法，同时证明了对上述两种蕴涵算子给出的求解算法均满足无条件还原性。但文献[15]仅考虑了蕴涵算子为R0和Lukasiewicz算子的情形，若蕴涵算子取别的算子，特别是在逻辑推理中有重要应用的正则蕴涵算子类，情况会如何呢？另外，文献[15]针对FMT问题（2）的SIS求解原则是在把大前提A→B等价地转化为B′→A′时提出的，但这只适用于满足换质位对称性的蕴涵算子（即满足等式 A(x)→B(y)=B′(y)→A′(x)的蕴涵算子），比如R0算子和Lukasiewicz算子，对更一般的蕴涵算子（特别是不具有换质位对称性的算子），文献[15]中给出的SIS FMT求解原则和求解算法则不再适用。本文在正则蕴涵算子的统一框架下，给出了基于SIS算法的FMP问题解的统一表达式，提出了一种改进的SIS FMT求解原则，并给出了基于该原则的FMT问题解的统一算法，进而证明了SIS FMP算法和SIS FMT算法均满足无条件还原性，最后讨论了FMP问题及FMT问题基于SIS算法的λ-水平解。

2　预备知识

定义1[6,16]设⊗:[0,1]2→[0,1]是二元函数，a,b,c∈[0,1]，I为指标集，若

（1）a⊗b=b⊗a

（2）(a⊗b)⊗c=a⊗(b⊗c)

（3）a⊗1=a

（4）若b≤c,则a⊗b≤a⊗c

则称⊗为[0,1]上的三角模，简称t-模，如果⊗还满足

则称⊗是左连续的三角模。

定义2[16]设R:[0,1]2→[0,1]是二元函数，⊗是[0,1]上的三角模，若a⊗b≤c当且仅当a≤R(b,c)，则称R是与⊗相伴随的蕴涵算子，R(b,c)也常记为b→c。当⊗是左连续的三角模时，则称与其相伴随的蕴涵算子为正则蕴涵算子。

下面给出几种常用的左连续的三角模和它们所对应的正则蕴涵算子。

3　基于正则蕴涵算子的SIS算法

注1当蕴涵算子为正则蕴涵算子时，由引理1（1）知式（3）的最大取值为1，从而FMP问题（1）的SIS解B*是使得下式成立的F(Y)中的最大模糊集:

4　正则蕴涵型λ-SIS算法

5　结束语

本文在正则蕴涵算子的统一框架下给出了SIS FMP以及SIS FMT求解算法的统一形式，证明了SIS FMP算法和SIS FMT算法都具有无条件的还原性，并给出了基于正则蕴涵算子的SIS算法的λ-水平解，为模糊控制领域中模糊推理方法的选择提供了更多的可能性。关于SIS FMP算法和SIS FMT算法的鲁棒性，将另文讨论。

[1]Zadeh L A.Outline of a new approach to the analysis of complex systems and decision processes[J].IEEE Transactions on Systems,Man and Cybernetics,1973,3(1):28-44.

[2]Cai Kaiyuan,Zhang Lei.Fuzzy reasoning as a control problem[J].IEEE Transactions on Fuzzy Systems,2006,14(6): 709-715.

[3]Ying Mingsheng.Perturbation of fuzzy reasoning[J].IEEE Transactions on Fuzzy Systems,1999,7(5):625-629.

[4]Perfilieva I,Lehmke S.Correct models of fuzzy IF-THEN rules are continuous[J].Fuzzy Sets and Systems,2006,157 (24):3188-3197.

[5]Wang Guojun.The full implication triple I method for fuzzy reasoning[J].Science in China:Series E,1999,29(1):43-53.

[6]Pei Daowu.Theory and applications of fuzzy logic based on triangular norms[M].Beijing:Science Press,2013.

[7]Wang Guojun,Fu Li.Unified forms of triple I method[J]. Computers and Mathematics with Applications,2005,49(5/6): 923-932.

[8]Pei Daowu.The unified algorithms of triple I methods for fuzzy reasoning[J].Information Sciences,2008,178(2): 520-530.

[9]Song Shiji,Feng Chunbo,Lee E S.Triple I method of fuzzy reasoning[J].Computers and Mathematics with Applications,2002,44(12):1567-1579.

[10]Wang Guojun,Duan Jingyao.On robustness of the full implication triple I inference method with respect to finer measurements[J].International Journal of Approximate Reasoning, 2014,55(3):787-796.

[11]Li Yongming,Li Dechao,Pedrycz W,et al.An approach to measure the robustness of fuzzy reasoning[J].International Journal of Intelligent Systems,2005,20(4):393-413.

[12]Li Yingfang,Qin Keyun,He Xingxing.Robustness of fuzzy connectives and fuzzy reasoning[J].Fuzzy Sets and Systems,2013,225(3):93-105.

[13]Dai Songsong,Pei Daowu,Wang Sanmin.Perturbation of fuzzy sets and fuzzy reasoning based on normalized Minkowski distances[J].Fuzzy Sets and systems,2012,189 (1):63-73.

[14]Dai Songsong,Pei Daowu.Robustness analysis of full implication inference method[J].International Journal of Approximate Reasoning,2013,54(5):653-666.

[15]Zou Xiangfu,Pei Daowu.SIS algorithms for fuzzy reasoning [J].Fuzzy Systems and Mathematics,2010,24(6):1-7.

[16]Wang Guojun,Zhou Hongjun.Introduction to Mathematical logic and Resolution Principle[M].Beijing:Science Press/ Oxford,UK:Alpha Science International Limited,2009.

附中文参考文献：

[5]王国俊.模糊推理的全蕴涵三I算法[J].中国科学:E辑, 1999,29(1):43-53.

[6]裴道武.基于三角模的模糊逻辑理论及其应用[M].北京:科学出版社,2013.

[15]邹祥福,裴道武.模糊推理的SIS算法[J].模糊系统与数学,2010,24(6):1-7.

LI Jun was born in 1972.He received the Ph.D.degree in uncertainty reasoning from Shaanxi Normal University in 2008.Now he is an associate professor at Lanzhou University of Technology.His research interests include computational intelligence and uncertainty reasoning,etc.

李骏（1972—），男，甘肃白银人，2008年于陕西师范大学获得博士学位，现为兰州理工大学理学院副教授，主要研究领域为计算智能，不确定性推理等。

BAI Lijun was born in 1989.She is an M.S.candidate at Lanzhou University of Technology.Her research interests include computational intelligence and uncertainty reasoning,etc.

白莉君（1989—），女，陕西渭南人，兰州理工大学理学院硕士研究生，主要研究领域为计算智能，不确定性推理等。

Unified Form and Reversibility of SISAlgorithms for Fuzzy Reasoningƽ

LI Jun+,BAI Lijun
School of Science,Lanzhou University of Technology,Lanzhou 730050,China

E-mail:lj99120@163.com

Fuzzy reasoning is the core of fuzzy control,the reversibility is one of most important evaluation standards for fuzzy reasoning algorithms.Under the framework of regular implication operators,this paper firstly gives the unified expression for solving FMP(fuzzy modus ponens)problems based on SIS(subsethood infer subsethood) method.Secondly,this paper proposes an improved SIS FMT(fuzzy modus tollens)algorithm and the unified form of its solution.In the end,this paper proves that the SIS FMP algorithm and SIS FMT algorithm are both unconditionally reversible,and studies theλ-solution of SIS algorithm for FMP and FMT.This algorithm will provide more alternative methods of fuzzy reasoning for the area of fuzzy control.

fuzzy control;fuzzy reasoning;regular implication operators;SIS algorithm

2015-07,Accepted 2015-09.

10.3778/j.issn.1673-9418.1507039

A

TP181

*The National Natural Science Foundation of China under Grant No.11261032(国家自然科学基金).

CNKI网络优先出版:2015-09-28,http://www.cnki.net/kcms/detail/11.5602.TP.20150928.1652.006.html

LI Jun,BAI Lijun.Unified form and reversibility of SIS algorithms for fuzzy reasoning.Journal of Frontiers of Computer Science and Technology,2016,10(10):1469-1474.