程序语言中基于Fibrations理论的索引共归纳数据类型*

苗德成，奚建清，戴经国

1.韶关学院 信息科学与工程学院，广东 韶关 512005

2.华南理工大学 软件学院，广州 510640

程序语言中基于Fibrations理论的索引共归纳数据类型*

苗德成1+，奚建清2，戴经国1

1.韶关学院 信息科学与工程学院，广东 韶关 512005

2.华南理工大学 软件学院，广州 510640

传统范畴论与共代数等方法在分析语义行为与描述共归纳规则方面存在不足，应用Fibrations理论对程序语言中索引共归纳数据类型（indexed co-inductive data type，ICDT）进行了研究。通过基变换构造索引Fibration，建立索引Fibration的等式函子与商函子等工具，应用伴随性质与保持等式的提升深入分析ICDT的语义行为；以此为基础，构造ICDT上参数化的共递归操作，在Fibrations理论框架内抽象描述具有普适意义的共归纳规则，并以实例分析简要介绍Fibrations理论在ICDT中的应用。与传统研究方法相比，Fibrations理论具有简洁的描述性与灵活的扩展性，可以精确分析ICDT的语义行为，具有高度的抽象性且不依赖特定的计算环境，描述了ICDT具有普适意义的共归纳规则。

语义行为；共归纳规则；基变换；提升；共递归

1　引言

作为一种语义计算能力更强的共归纳数据类型[1]，ICDT（indexed co-inductive data type）以共代数[2-3]为数学基础，将终结性与互模拟等工具引入类型理论研究中，在程序语言动态语义行为分析等方面具有独特的优势。Fibrations理论是计算机科学基础研究的一个新兴方向，特别是在范畴论方法研究领域，已成为前沿热点。同时，在数据库系统建模[4-5]、软件规范[6]和程序设计方法[7-8]等领域也有广泛的应用，为有效描述形式系统间的结构化联系提供了一种通用的思维方法、研究手段和理论工具。

从文献检索的情况看，Hagino最早应用Dialgebras结构与范畴论方法分析了归纳与共归纳数据类型间的关系[9]，奠定了共归纳数据类型的研究基础，但在继承、多态类型系统与共归纳原理等方面存在一定的不足。Poll基于子类型和继承对Hagino的工作进行了拓展，应用代数与共代数的对偶性质研究了归纳与共归纳数据类型的子类型和继承关系[10]。Nogueira等人应用双代数（bialgebra）方法研究了归纳与共归纳数据类型的关系及其在多态编程中的应用[11]。文献[12]利用λ-双代数与分配律将归纳与共归纳数据类型有机融合起来，探讨语法构造与动态行为关系，而文献[13]进一步给出了强共归纳数据类型的定义及一种带固定参数的共递归操作punfold，并结合共模态共递归给出unfold与punfold的结构化描述，同时分析了punfold上的各种计算律。Greiner与Hinze将共归纳原理引入到程序语言中，对程序语言中的共归纳数据类型进行了深入研究[1,14]。以上研究成果在一定程度上解决了上述问题。

Hermida与Jacobs证明了有商类型的终结共代数的共归纳规则是可靠的[15]。Ghani等人在文献[15]的基础上，突破多项式函子的限制，进一步将其研究工作扩展为一般意义上的函子类型[7,16]。同时，文献[16]分析了ICDT与其语义行为在程序逻辑上的对应关系。文献[17]在Jacobs等人研究的基础上[15]，证明了Fibrations环境下互模拟共归纳证明方法的可靠性，并通过参数变换提出弱互模拟性证明的一种新范畴论方法。文献[18]基于自反图（reflexive graphs）提出了依赖数据类型的一种参数化模型，该模型可被视为从族fibration到其自反图fibration的一种转换，支持初始代数存在性的判定与推导。

最近，Ghani与Revell等人提出λ1-fibration的概念，以限定于卡式闭范畴的基范畴描述单位消除语义，以全范畴描述关系语义，并由λ1-fibration归纳地构造参数化计量单位fibrationUoM，证明了UoM的一些基本定理，给出一些UoM实例，在范畴论的层面对Kennedy的工作[19]进行了扩展[20]。Dorel等人应用共归纳原理提出了一个4规则的逻辑演绎系统来证明程序的等价性，并证明了该系统的可靠性与弱完备性[21]。Laura针对云存储架构中的弱存储模型与结果一致性存储等问题，基于共归纳原理和进程演算引入存储状态兼容性的概念，在云存储行为上进行共归纳推理，支持异构多源数据类型的描述[22]。

现有研究成果主要集中在共归纳数据类型及其在程序语言中的应用，而ICDT的研究当前还处于起步阶段，在语义计算与程序逻辑等方面存在许多尚未解决的问题，如语义行为的分析与共归纳规则的描述等，特别是共归纳规则多以自动生成为主，缺乏坚实的数学基础和精确的形式化描述。同时，传统方法在局部卡式闭范畴内建立ICDT的类型论模型，使得ICDT与描述其语义行为的关系共存于同一个范畴内，导致自函子与其提升是等同的，在语义行为分析与共归纳规则描述方面存在一定的局限性。

针对以上问题，本文应用Fibrations理论对ICDT进行了研究。突破传统方法对局部卡式闭范畴的限制，描述ICDT语义行为的关系不再局限于函数或态射，而是提升为全范畴中的对象。同时，ICDT与描述其语义行为的关系不再共存于同一个范畴内，构造索引fibration及其等式函子等工具，并应用伴随性质与保持等式的提升在共代数范畴内深入分析ICDT的语义行为；构造ICDT上参数化的共递归操作，抽象描述具有普适意义的共归纳规则。

本文组织结构如下：首先，在切片范畴（slice category）上构造索引fibration及其等式函子等工具，深入分析ICDT的语义行为；其次，以此为基础构造索引fibration基范畴上参数化的共递归操作，抽象描述具有普适意义的共归纳规则；再次，辅以实例简要介绍Fibrations理论在ICDT中的应用；最后，总结全文并给出后续研究工作。

2　预备知识

本文假定读者具备拉回（pullback）、图表交换（diagram commute）与终对象（terminal object）等范畴论与共代数基础。若范畴全体对象与态射都构成集合，则该范畴是小范畴（small category）[23]，本文的研究对象均基于小范畴。卡式射（Cartesian arrow）、fibration等Fibrations理论的基础内容可参见文献[3, 24-26]等。记id为单位态射，Id为单位函子，1为终对象，Obj C为范畴C的对象集，Mor C为范畴C的态射集。

定义1（纤维）设P:T→B是两个小范畴T、B间的一个fibration，称B为基范畴，T为全范畴。对基范畴B中的一个对象C，∃X∈Obj T，k∈Mor T，若有P(X)=C与P(k)=idC，则X与k构成的子范畴TC称为对象C上的纤维，并称k为垂直态射。

实际上，fibration是一种确保大量卡式射存在的函子，而纤维TC是全范畴T的一个全子范畴（full subcategory）。opfibration是fibration的对偶概念，若函子P:T→B既是一个fibration，又是一个opfibration，则称P为bifibration。

定义2（重索引函子）基范畴B中的态射 f:C→D扩展为纤维TD与TC间的函子 f*:TD→TC，称 f*为由 f归纳的重索引函子。

定义3（对偶重索引函子）基范畴B中的态射f:C→D扩展为纤维TC与TD间的一个函子*f:TC→TD，称*f为由 f归纳的对偶重索引函子。

3　ICDT的语义行为

基于Fibrations理论的观点，ICDT是一种常见的带有离散索引对象的共归纳数据类型，如流、表与树及带环无限循环图等复杂的数据结构，支持协同进程演算及其控制过程等。本文通过基变换构造索引fibration及其等式函子等工具，在共代数范畴内应用伴随函子的伴随性质与保持等式的提升，对ICDT的语义行为进行深入分析，增强程序语言对ICDT语义行为的处理与证明能力。

3.1真值函子与关系fibration

定义4（纤维化终对象）设P:T→B是两个小范畴T、B间的一个fibration，取∀D∈Obj B，若∃1D∈ObjTD为纤维TD上的终对象，且∀f:C→D∈Mor B，f*(1D)为纤维TC上的终对象，即重索引函子 f*保持终对象，则称fibrationP有纤维化终对象。

定义5（真值函子与内涵函子）设P:T→B是两个小范畴T、B间的一个fibration，函子TP:B→T将∀C∈Obj B映射为纤维TC上的终对象，称TP为fibrationP的真值函子。若TP有一个右伴随函子{-}，则称{-}为P的内涵函子。

记1B与1T分别为基范畴B与全范畴T的终对象，则有P(1T)=1B。对∀C∈Obj B，存在唯一的态射u:C→1B，有。对 ∀f:C→D∈Mor B，，真值函子TP将 f映射为全范畴T上的卡式射。

例1设Set为集合范畴，∀X∈Obj Set，X上的一个谓词是一个二元组，其中，P:X→Set。对∀x∈X，P(x)构成一个集合，描述x的语义行为，并称X为谓词的定义域。谓词到的态射是一个序对(f,f～):→，其中f:X→X′是相应谓词定义域上的函数，而对∀x∈X,f～:P(x)→P′(f(x))，将P(x)映射为P′(f(x))。谓词及其态射构成谓词范畴 P，进而得到谓词fibration Pre:P→Set，将全范畴P的对象映射为X。对 f:X→Y∈Mor Set，有P:Y→Set∈Obj P，则 f与的卡式射为谓词范畴 P中的一对态射。谓词fibrationPre的真值函子TPre将X映射为谓词范畴P的单点集谓词<{*},P>，P:{*}→Set。谓词fibrationPre的内涵函子{-}将谓词映射为语义行为集{P(x)|x∈X}。

定义6（P的关系fibration）设P:T→B为两个小范畴T、B间的一个fibration，基范畴B有积。令Δ:B→B为B上的对角自函子，将∀C∈Obj B映射为积对象C×C。P沿Δ的拉回构成fibrationRel(P): Rel(T)→ B，称Rel(P)为P的关系fibration。

Rel(P)全范畴Rel(T)的对象为关系(C,D)，对另一对象(C′,D′)，令 f:C→C′，g:D→D′，(f,g):(C,D)→(C′, D′)∈Mor Rel(T)。图1中的关系fibrationRel(P)将关系(C,D)映射为基范畴B中的对象C，函子Π将(C,D)映射为T中的对象D，且有P(D)=Δ(C)。同时，定义6的拉回保持性质确保C上关于Rel(P)的纤维Rel(T)C与C×C上关于P的纤维TC×C是同构的，即。

由给定的fibration通过拉回构造一个新的fibration的过程称为基变换，如定义6中P通过基变换构造Rel(P)。基变换具有保持结构的性质，如保持纤维化终对象[27]，即若P有真值函子TP，则Rel(P)有真值函子TRel(P)，且TRel(P)(C)=TP(C×C)。

设P:T→B是一个bifibration，基范畴B有拉回。若对B中任意一个拉回方形，如图2所示，自然变换*s∘t*→g*∘*f是一个同构，则称P满足Beck-Chevalley条件。Beck-Chevalley条件（简称BC条件）实际上是由bifibrationP的基范畴中一个拉回方形定义了全范畴T中各相关纤维间函子保持结构的一种自然变换，进而确保重索引与对偶重索引函子满足合适的图表交换性质。

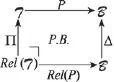
Fig.1　Relation fibrationRel(P)ofP图1　P的关系fibrationRel(P)

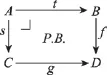
Fig.2　Apullback square in base categoryBon bifibration图2　bifibration基范畴B中任意一个拉回方形

定义7（等式函子）设P:T→B是一个满足BC条件的bifibration，B有积，且TP为P的真值函子。对∀C∈Obj B，自然变换δ:IdB→Δ在C的作用函数δC:C→C×C扩展为对偶重索引函子*δ，称EqP:B→Rel(T)为P的等式函子，EqP=*δ∘TP。

真值函子TP将C映射为TC上的终对象TP(C)，由定义6知Rel(P)是P沿Δ的基变换，则若P有纤维化终对象，则Rel(P)也有纤维化终对象。定义7中的*δ将TP(C)映射为*δ(TP(C))，而Rel(T)C)，且P的等式函子EqP将∀f∈Mor B映射为δf与确定的 f×f上唯一态射。等式函子的直观意义是，相同的参数得到相同的结果[15]。

3.2索引fibration与其等式函子

定理1设P:T→B是两个小范畴T、B间的一个fibration或bifibration，TP:B→T为 P的真值函子。∃I∈Obj B为基范畴B上的离散索引对象，令索引函子P/I:T/TP(I)→B/I为对∀u:Y→TP(I)∈Obj T/TP(I)，有P/I(u)=P(u):P(Y)→I∈Obj B/I，则索引函子P I也是一个fibration或bifibration。

证明 取∀f:C→D∈Mor B，存在 f上fibrationP的卡式射，使得P(X)=D，且存在唯一态射w:TP(I)→f*(X)，有与P(v)=f∘h，如图3所示。设α:D→I∈Obj B/I，β:C→I∈Obj B/I，则有γ:P(u)→α=P(Y)→D∈Mor B/I，δ:P(u)→β=P(Y)→C∈Mor B/I，满足图表交换γ=f∘δ。在函子P I的全范畴T/TP(I)中，s:X→TP(I)∈Obj T/TP(I)，t:f*(X)→TP(I)∈Obj T/TP(I)，有g:u→s=Y→X∈Mor T/TP(I)，则存在唯一态射k:u→t=Y→f*(X)，满足图表交换，故是 f上函子P I的卡式射，即如果P是一个fibration，则索引函子P I也是一个fibration。

Fig.3　Cartesian arrowof functorP Ionf图3　f上函子P I的卡式射

设m:Z→TP(I)∈Obj T/TP(I)，由函子P I的定义有P/I(m)=α，令为 f上P的对偶卡式射，如图4所示。切片范畴B I中有图表交换α=β∘f，函子P I全范畴T/TP(I)中存在唯一态射n:*f(Z)→ TP(I)，满足图表交换，故是 f上函子P I的对偶卡式射，即如果P是一个opfibration，则索引函子P I也是一个opfibration。

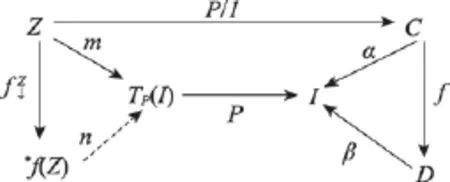
Fig.4　Opposite Car tesian arrowof functorP Ionf图4　f上函子P I的对偶卡式射

综上，如果P是一个bifibration，则索引函子P I也是一个bifibration。□

定理1证明了索引fibrationP I与fibrationP具有相同的fibration或bifibration性质，同时也对索引fibration进行了定义。实际上，P沿定义域函子dom:B/I→B的基变换可具体构造一个索引fibration P/I:T/TP(I)→B/I，对∀α:C→I∈Obj B I，P在C上的纤维TC与P I在α上的纤维(T/T(I))α是同构的[16]，且若P有真值函子，由P构造的索引fibrationP I也有真值函子。

对∀α:C→I∈Obj B/I，设α沿自身的拉回分别为i与 j，则积对象α×α为α∘i或α∘j，即切片范畴B I的积对象由其拉回确定。与定义6类似，下面给出索引fibrationP I的关系fibration的定义。

定义8（P I的关系fibration）令P/I:T/TP(I)→B/I为一个索引fibration，基范畴 B I有积。设Δ/I:B/I→B/I为切片范畴B I上的对角自函子，将∀α∈B/I映射为其积对象α×α。P I沿Δ I的拉回构成fibrationRel(P/I):Rel(T/TP(I))→B/I，称Rel(P/I)为P I的关系fibration。

对Rel(P/I)在α上对象R∈Obj Rel(T/TP(I))，P I在α×α上对象R′∈Obj T/TP(I)，P在dom(α×α)上对象R″∈ObjT，有同构表达式R≅R′≅R″成立[16]。α在自然变换 δ/I:IdBI→Δ/I上的作用函数为 (δ/I)α: C→dom(α×α)，则自然变换δ I的直观意义是将切片范畴中B I的一个对象变换为另一个对象的态射。与定义7类似，下面给出索引fibrationP I的等式函子的定义。

定义9（P I的等式函子）设P:T→B是一个满足BC条件的bifibration，P有真值函子，且基范畴B有积。令索引fibrationP I的真值函子为TPI，称EqPI=*(δ/I)∘TPI:B/I→Rel(T/TP(I))为P I的等式函子。

等式函子EqPI将切片范畴B I中的对象α:C→I映射为α×α上的唯一态射*(δ/I)α∘TPI(C)→TP(I)。下面构造索引fibrationP I的商函子。

3.3商函子与保持等式的提升

以fibrationP:T→B的等式函子EqP:B→Rel(T)替代 P的真值函子TP:B→T，P的关系fibration Rel(P)替代P，应用定理1，构造一个新的fibration Rel(P)/I:Rel(T)/EqP(I)→B/I，对 ∀R∈Obj Rel(T)，Rel(P)/I将α:R→EqP(I)映射为α′:QR→I，α′是α在伴随函子下的置换。

设∀R=(C,D)∈Obj Rel(T/TP(I))，则QPI(C,D)=C，如图5所示。Π(C,D)=D，对 f:D→TP(I)∈Obj T/TP(I)，P/I(f)=P(D)→I，而对g:C→I∈Obj B/I，Δ/I(g)=g×g，即dom(g×g)=P(D)。

Fig.5　Construction of quotient functorQPI图5　商函子QPI的构造

例2记Set为集合范畴，I为一离散索引对象，则 Set在 I上的切片范畴为Set/I。对任意集合X∈Obj Set，存在X/I∈Obj Set/I。索引fibrationP I的关系fibration为Rel(P/I)，X I关于Rel(P/I)在Set/I上的纤维Rel(T/TP(I))XI由关系R:X/I×X/I→Set/I构成，即 Rel(T/TP(I))XI={R:X/I×X/I→Set/I|X/I∈Obj Set/I}。对X I中任意两个对象α与α′，R(α,α′)给出α与α′某种关联性（如等价、同余、同构等）的构造证明，如构造 R的一种等价性定义:若α≅α′，R(α,α′)=1；否则R(α,α′)=0，其中≅为等价。索引fibrationP I的等式函子EqPI将X I映射为关联集R(X/I,X/I)，而商函子QPI则将关联集R(X/I,X/I)映射为X I的商集(X/I)/R，(X/I)/R由含R的最小等价关系确定。

定义12（保持等式的提升）设P:T→B为一个满足BC条件且有真值函子TP的bifibration，基范畴B有积与拉回，P/I:T/TP(I)→B/I是P的索引fibration，构造P I的关系fibrationRel(P/I)，并有P I的等式函子EqPI与商函子QPI。F是Rel(P/I)基范畴B I上的一个自函子，F⊥是Rel(P/I)全范畴Rel(T/TP(I))上的一个自函子，若满足图表交换Rel(P/I)∘F⊥=F∘Rel(P/I)，且有同构表达式 EqPI∘F≅F⊥∘EqPI与F∘QPI≅QPI∘

F⊥成立，则称F⊥是F关于Rel(P/I)在全范畴Rel(T/TP(I))上的一个保持等式的提升。

3.4ICDT的语义行为

对∀α:C→I∈Obj B/I，在自函子F作用下构成一个F-共代数(α,r:α→F(α))，称α为载体（carrier）。(α,r)与另一F-共代数(β,t:β→F(β))的态射是r与t载体间的态射 f:α→β，并且满足图表交换t∘f= F(f)∘r。

定理2以F-共代数为对象，以F-共代数态射为态射，构成F-共代数范畴CoalgF。

证明 设dom:Mor CoalgF→Obj CoalgF为域函数，cod:Mor CoalgF→Obj CoalgF为共域函数，下面证明CoalgF是一个范畴。

令(α,r)，(β,t)，(γ,s)∈Obj CoalgF，f:(α,r)→(β,t)，g: (β,t)→(γ,s)∈Mor CoalgF，则 g∘f:(α,r)→(γ,s)∈Mor CoalgF，故dom(g∘f)=dom(f)=(α,r)，cod(g∘f)=cod(g)= (γ,s)，满足匹配条件。

设h:(γ,s)→(δ,v)∈Mor CoalgF，h∘g:(β,t)→(δ,v)∈Mor CoalgF，故h∘(g∘f)=(α,r)→(δ,v)=(h∘g)∘f，满足结合律条件。

对(α,r)∈Obj CoalgF，存在一个唯一的单位态射id(α,r)，有dom(id(α,r))=cod(id(α,r))=(α,r)，且对∀f∈Mor CoalgF，若dom(f)=(α,r)，则 f∘id(α,r)=f；若cod(f)=(α,r)，则id(α,r)∘f=f，满足单位态射存在条件。

由范畴的定义[26]知，CoalgF是一个由F-共代数及其态射构成的F-共代数范畴。□

终结F-共代数(νF,out:νF→F(νF))若存在，则是唯一同构的。终结共代数具有终结性的泛性质，其所确定的唯一同构性是研究ICDT语义行为的主要工具。

作为终结F-共代数载体的ICDTνF是函子F的最大不动点（maximal fixed point），函子F指称ICDT νF的语法析构（destructor），out从外部观察νF在该语法析构过程中一种语义行为。应用索引fibration P I的等式函子EqPI，将F-共代数(α,r)映射为一个F⊥-共代数 EqPI(α,r)=(EqPI(α),EqPI(r):EqPI(α)→EqPI(F(α))≅F⊥(EqPI(α)))。相应地，EqPI(νF)为终结F⊥-共代数的载体，即等式函子EqPI保持终对象。

定理3以F⊥-共代数为对象，以F⊥-共代数态射为态射，构成F⊥-共代数范畴CoalgF⊥。

证明证明过程与定理2类似，略。□

记Coalg(EqPI)为CoalgF到CoalgF⊥的函子，利用等式函子EqPI将关系fibrationRel(P/I)基范畴B I中的对象与态射映射为全范畴Rel(T/TP(I))中相应的对象与态射，并通过函子Coalg(EqPI)进一步建立CoalgF到CoalgF⊥的联系。

令(EqPI(νF),out⊥:EqPI(νF)→F⊥(EqPI(νF)))是关系fibrationRel(P/I)全范畴Rel(T/TP(I))中的一个终结F⊥-共代数，则out⊥是out在函子Coalg(EqPI)作用下的同态（homomorphism）像，即Coalg(EqPI)(out)=out⊥。终结F⊥-共代数的终结性确保out⊥是唯一同构的，唯一同构泛性质的存在为分析ICDT的语义行为提供了极大的便利性。

与Coalg(EqPI)类似，记Coalg(QPI)为CoalgF⊥到CoalgF的函子，由伴随函子的伴随性质有对任一 F⊥-共代数 (ω,q:ω→F⊥(ω))， ω:X→TP(I)∈Obj Rel(T/TP(I))，有Coalg(QPI)(q)=QPI(ω)→QPI(F⊥(ω))≅F(QPI(ω))，即 Coalg(QPI)(q)=QPI(q)，则QPI(q)是q在函子Coalg(QPI)作用下的同态像，如图6所示。若g:ω→EqPI(α)是q到EqPI(r)的F⊥-共代数态射，则QPI(q)到r的F-共代数态射h:QPI(ω)→α是g上的F-共代数同态。类似地，g是h上的F⊥-共代数同态。

Fig.6　Coalgebra category functor Coalg(EqPI)andCoalg(QPI)图6　共代数范畴函子Coalg(EqPI)与Coalg(QPI)

函子Coalg(EqPI)的左伴随Coalg(QPI)建立以QPI(ω)为载体的F-共代数与以ω为载体的F⊥-共代数间直观的互推导关系，为ICDT的语义行为分析提供了一种以νF为终结共代数载体的简洁与一致的建模方法。

4　ICDT的共归纳规则

对定义并运用了等式函子与商函子的fibration，ICDT共归纳规则的形式化描述与语义行为分析是一致的[15]。设fibrationP:T→B与索引fibrationP/I: T/TP(I)→B/I满足定义12。F是P I的关系fibration Rel(P/I)的基范畴B I上的一个自函子，νF为终结F-共代数的载体，且F⊥为F关于Rel(P/I)保持等式的提升，则P I有以νF为ICDT的共归纳规则。同时，若函子Coalg(EqPI)保持终对象，则F⊥生成一个可靠的共归纳规则。这为F⊥应用终结F-共代数在ICDT上生成共归纳规则的有效性（validity）判定提供了一种可靠依据，即若索引fibrationP I定义并运用等式函子与商函子分析ICDT的语义行为，则其基于终结F-共代数的共归纳规则在程序语言语义行为分析过程中是有效的。下面在Fibrations理论框架内提出并抽象描述ICDT具有普适意义的共归纳规则。

基于范畴论的观点，共归纳数据类型的共递归计算源于终结共代数语义[2]。设∀α:C→I∈Obj B/I，令νF∈Obj B/I，应用F构造基范畴B I上ICDT的共递归操作unfold:(α→F(α))→α→νF。对任意一个F-共代数(α,r:α→F(α))，unfold r将(α,r)映射为r到终结F-共代数(νF,out)的唯一F-共代数态射unfold r:α→νF。源于终结共代数语义的unfold本质上是共归纳数据类型一个参数化（parameterized）的共递归操作，其共递归计算具有语义正确，扩展灵活与表达简洁等良好性质。

由定义12可知，EqPI(F(α))≅F⊥(EqPI(α))，EqPI(F(νF))≅F⊥(EqPI(νF))，而等式函子 EqPI保持终对象，则EqPI(νF)为终结F⊥-共代数的载体，记νF⊥= EqPI(νF)，X=EqPI(α)。应用自函子F⊥构造全范畴Rel(T/TP(I))上ICDT共递归操作unfold:(X→F⊥(X))→X→νF⊥。

对任意一个F⊥-共代数(X,q:X→F⊥(X))，unfold q将q映射为(X,q)到终结F⊥-共代数(νF⊥,out⊥)的唯一F⊥-共代数态射unfold q:X→νF⊥。对∀α∈Obj B/I，∃X∈Obj Rel(T/TP(I))，有ICDT具有普适意义的共归纳规则:CoindUni:(X→F⊥(X))→X→EqPI(νF)。

若(X,q:X→F⊥(X))是F-共代数(α,r:α→F(α))上的F⊥-共代数，则CoindUniX q是unfold r上的F⊥-共代数同态。

5　实例分析

例3流或无穷序列的元素类型由索引I指定，如自然数类型Nat，整型Int与字符型Char等，∀I∈Obj B。对任意流α:S→I∈Obj B/I，有B I上自函子F:α→I×α，其中head:α→I为流的头函数，tail:α→α为去掉头元素后的尾函数。应用定理1构造索引fibrationP I，并取P I的关系fibrationRel(P/I)全范畴Rel(T/TP(I))中任一流性质R∈Obj Rel(T/TP(I))，如互模拟，则对B I中另一流对象β:S′→I，有α与β在互模拟性质R上的一个共归纳成立。

R是两个流类型α与 β间的互模拟关系，当且仅当∀(α,β)∈R，head(α)=head(β)，且(tail(α),tail(β))∈R。

由定理2知F-共代数及其态射构成F-共代数范畴CoalgF，若CoalgF中终结F-共代数(νF,out: νF→F(νF))存在，令流类型Stream(I)为该终结F-共代数的载体νF。自函子F应用定义12可构造一个保持等式的提升F⊥，F⊥-共代数及其态射应用定理3可构成F⊥-共代数范畴CoalgF⊥。对CoalgF中任一F-共代数(α,r:α→F(α))，通过关系fibrationRel(P/I)提升为CoalgF⊥中的一个F⊥-共代数(X,q:X→F⊥(X))，满足图表交换F∘Rel(P/I)(X)=Rel(P/I)∘F⊥(X)。终结F-共代数的终结性定义Stream(I)上一个共递归操作unfold r，执行Stream(I)的判定；而由终结F⊥-共代数的终结性对应得到一个共递归操作，描述Stream(I)的语义行为。若q位于r上，则CoindUniX q是unfold r上的F⊥-共代数同态，且遍历关系fibrationRel(P/I)全范畴Rel(T/TP(I))中每一性质R，R∈Obj Rel(T/TP(I))，得到描述Stream(I)行为的语义集{R(X,X)|X=EqPI(α),∀α∈Obj B/I}。

例3中的unfold r直观描述了流类型α到其语义行为的映射关系。unfold r的存在性提供了共代数到其终结共代数同态射的一种有效方式，进而得到共归纳定义原则，即定义函数unfold r:α→Stream(I)，只需在α上构造相应操作r，令(α,r)成为一个F-共代数即可，F(α)=I×α。同时，unfold r的唯一性进一步证明两个同态射相等，从而得到共归纳证明原则，即证明m,n:α→Stream(I)相等，只需证明m与n都是同一个共代数(α,r)到其终结F-共代数(Stream(I),out: Stream(I)→F(Stream(I)))的同态射即可，即证明m与n都等于unfold r。

相对于传统的范畴论与共代数研究方法，例3具有同样的表达能力，但在语义行为分析与共归纳规则描述方面比前者更强，如表1所示。例如，互模拟是共代数与自动机理论研究的核心内容，例3从Fibrations理论的角度进一步拓展传统共代数方法的研究内容，在关系fibrationRel(P/I)上建立描述Stream(I)共递归计算的共归纳规则CoindUni，突破传统方法多以自动生成共归纳规则为主的局限，提供一种精确、简洁的形式化描述方式。特别是在函数式程序语言（如Haskell、ML等）中，CoindUni生成的代码片段具有易读、易写与易理解等良好性质。

Table 1　Expression abilities between Fibrations and traditional methods表1　Fibrations理论与传统方法的表达能力比较

例4确定有穷状态自动机（deterministic finite automaton，DFA）状态空间K的具体类型由离散索引对象I指定，如字母、数字与时间序列等，∀I∈Obj B。Σ为DFA的有限输入表，B I上自函子F:K×Σ→K为状态转移函数。记1为终对象，ε为空输入。对K中的任意状态x:K→I∈Obj B/I，a∈Σ，若F(x,a)=1，则DFA停机；F(x,a)∈K，则DFA成功运行并产生一个新状态。应用定理1构造索引fibrationP I，并取P I的关系fibration全范畴中任一DFA性质U∈Obj Rel(T/TP(I))，如可达性，则对另一状态x′:K→I，输入a时有从状态x到x′可达的一个共归纳成立:

若CoalgF中终结F-共代数(νF,out:νF→F(νF))存在，令DFA(I)为该终结F-共代数的载体νF。应用定义12由F可构造一个保持等式的提升F⊥。对CoalgF中任一F-共代数(τ,l:τ→F(τ))，通过关系fibrationRel(P/I)提升为CoalgF⊥中的一个F⊥-共代数(Z,m:Z→F⊥(Z))，满足图表交换 F∘Rel(P/I)(Z)= Rel(P/I)∘F⊥(Z)。由终结 F-共代数的终结性定义DFA(I)上一个共递归操作unfold l，执行DFA(I)的判定；而由终结F⊥-共代数的终结性对应得到一个共递归操作，描述DFA(I)的语义行为。若m位于l上，则CoindUniZ m是unfold l上的F⊥-共代数同态，且遍历全范畴Rel(T/TP(I))中每一性质U，得到描述DFA(I)行为的语义集{U(Z,Z)|Z=EqPI(τ),∀τ∈Obj B/I}。

可达性是自动机理论研究的重要内容，例4在统一的Fibrations理论框架内研究自动机状态的可达性具有较强的普适意义，脱离不相关的语法细节，直接面向特定的领域问题。传统研究方法中，操作语义方法证明自动机中两个状态在语义行为上等价，指称语义方法证明两个状态在语义模型中指称同一个对象，而数理逻辑方法则证明程序语言的两个状态在所有可能的模型中映射到同一个对象。以上3种方法依赖于操作语义、指称语义与类型论等特定的计算环境，缺乏通用的建模概念，不具有普适意义。在建模工具的普适性方面，Fibrations理论与传统方法的比较如表2所示。

Table 2　Universality between Fibrations and traditional methods表2　Fibrations理论与传统方法的普适性比较

6　结束语

本文基于切片范畴B I建模，较好地处理了以I为索引的单类ICDT的语义行为及其共归纳规则的分析与描述，但I只是针对单类特定的ICDT，难以有效处理互递归（mutual recursive）等更为复杂的多类ICDT。将单类索引fibration的离散索引对象I扩充为索引范畴C，构造多类索引fibration，以Obj C为索引集描述B中的多类ICDT，在索引范畴C上基于fibrationG:B→C进行多类ICDT的语义行为建模，针对不同的索引选择不同的程序逻辑，是下一步的研究工作。同时，初步探讨ICDT及其共归纳规则构成复杂形式系统的可靠性、完备性与一致性等元性质。另外，应用Fibrations理论将ICDT的研究成果推广到2-范畴，深入探讨程序语言语义计算与程序逻辑在高阶范畴中的数学结构和范畴性质也是下一步研究工作的重点。

[1]Greiner J.Programming with inductive and co-inductive types, CMU-CS-92-109[R].Pittsburgh,USA:School of Computer Science,Carnegie Mellon University,1992.

[2]Rutten J.Universal coalgebra:a theory of systems[J].Theoretical Computer Science,2000,249(1):3-80.

[3]Zhou Xiaocong,Shu Zhongmei.A survey on the coalgebraic methods in computer science[J].Journal of Software,2003,14(10):1661-1671.

[4]Johnson M,Rosebrugh R.Fibrations and universal view updatability[J].Theoretical Computer Science,2007,388(1/3): 109-129.

[5]Johnson M,Rosebrugh R,Wood R J.Lenses,fibrations and universal translations[J].Mathematics Structure in Computer Science,2012,22(1):25-42.

[6]Tews H.Coalgebra method for object-oriented specification [D].Dresden,Germany:Institute of Theoretical Information,Technical University Dresden,2002.

[7]Ghani N,Johann P,Fumex C.Generic fibrational induction[J]. Logical Methods in Computer Science,2012,8(2):1-27.

[8]Miao Decheng,Xi Jianqing,Jia Lianyin,et al.Formal language algebraic model[J].Journal of South China University of Technology:Natural Science Edition,2011,39(10):74-78.

[9]Hagino T.A Categorical programming language[D].Edinburgh,UK:Laboratory for Foundations of Computer Science,Department of Computer Science,University of Edinburgh,1987.

[10]Poll E.Subtyping and inheritance for categorical data types[J]. Sūrikaisekikenkyūsho Kōkyūroku,1998,1023:112-125.

[11]Nogueira P,Moreno-Navarro J.Bialgebra views:a way for polytypic programming to cohabit with data abstract[C]// Proceedings of the 2008 ACM SIGPLAN Workshop on Generic Programming,Victoria,Canada,Sep 20,2008.New York:ACM,2008:61-73.

[12]Su Jindian,Yu Shanshan.Coinductive data types and their applications in programming languages[J].Computer Science,2011,38(11):114-118.

[13]Su Jindian,Yu Shanshan.Comonadic corecursions on strong coinductive data types[J].Journal of South China University ofTechnology:Natural Science Edition,2014,42(1):128-134.

[14]Hinze R.Reasoning about Codata[C]//LNCS 6299:Central European Functional Programming School,Third Summer School,Budapest,Hungary,May 21-23,2009.Berlin,Heidelberg:Springer,2010:42-93.

[15]Hermida C,Jacobs B.Structural induction and coinduction in a fibrational setting[J].Information and Computation, 1998,145(2):107-152.

[16]Ghani N,Johann P,Fumex C.Indexed induction and coinduction,fibrationally[J].Logical Methods in Computer Science,2013,9(3/6):1-31.

[17]Bonchi F.Petrisan D,Pous D,et al.Coinduction up-to in a fibrational setting[C]//Proceedings of the Joint Meeting of the 23rd EACSL Annual Conference on Computer Science Logic and the 29th Annual ACM/IEEE Symposium on Logic in Computer Science,Vienna,Austria,Jul 14-18,2014.New York:ACM,2014:1-18.

[18]Atkey R,Ghani N,Johann P.A relationally parametric model of dependent type theory[J].ACM SIGPLAN Notices,2014, 49(1):503-515.

[19]Kennedy A J.Relational parametricity and units of measure [C]//Proceedings of the 24th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages,Paris, France,Jan 1997.New York:ACM,1997:442-455.

[20]Ghani N,Revell T,Atkey R,et al.Fibrational units of measure[EB/OL].[2015-03-21].https://personal.cis.strath.ac.uk/ neil.ghani/pub.html.

[21]Dorel L,Vlad R.Program equivalence by circular reasoning[J]. FormalAspects of Computing,2015,27(4):701-726.

[22]Laura B,Hernán M.On the behavior of general purpose applications on cloud storages[J].Service Oriented Computing andApplications,2015,9(3):213-227.

[23]Barr M,Wells C.Category theory for computing science[M]. New York:Prentice-Hall,1990:252-270.

[24]Pavlovic D.Predicates and fibrations[D].Utrecht,Nederland:University of Utrecht,1990.

[25]Jacobs B.Categorical logic and type theory[M].Amsterdam,Nederland:Elsevier Science,2001:20-107.

[26]Qu Yanwen.Formal semantics foundation and formal description[M].2nd ed.Beijing:Science Press,2010:118-172.

[27]He Wei.Category theory[M].Beijing:Science Press,2006: 23-44.

附中文参考文献：

[3]周晓聪,舒忠梅.计算机科学中的共代数方法的研究综述[J].软件学报,2003,14(10):1661-1671.

[8]苗德成,奚建清,贾连印,等.一种形式语言代数模型[J].华南理工大学学报:自然科学版,2011,39(10):74-78.

[12]苏锦钿,余珊珊.程序语言中的共归纳数据类型及其应用[J].计算机科学,2011,38(11):114-118.

[13]苏锦钿,余珊珊.强共归纳数据类型上的Comonadic共递归[J].华南理工大学学报:自然科学版,2014,42(1):128-134.

[26]屈延文.形式语义学基础与形式说明[M].2版.北京:科学出版社,2010:118-172.

[27]贺伟.范畴论[M].北京:科学出版社,2006:23-44.

MIAO Decheng was born in 1979.He received the Ph.D.degree in computer application technology from South China University of Technology in 2012.Now he is an associate professor at Shaoguan University.His research interests include formal languages theory and category theoretical methods,etc.

苗德成（1979—），男，黑龙江伊春人，2012年于华南理工大学获得博士学位，现为韶关学院副教授，主要研究领域为形式语言理论，范畴论方法等。

XI Jianqing was born in 1962.He received the Ph.D.degree in computer architecture from National University of Defense Technology in 1992.Now he is a professor and Ph.D.supervisor at South China University of Technology. His research interests include database and software theory,etc.

奚建清（1962—），男，江苏无锡人，1992年于国防科技大学获得博士学位，现为华南理工大学教授、博士生导师，主要研究领域为数据库，软件理论等。

DAI Jingguo was born in 1962.He received the M.S.degree in software engineering from Wuhan University in 1994.Now he is a professor and M.S.supervisor at Shaoguan University.His research interests include formal semantics and sound software,etc.

戴经国（1962—），男，湖南双峰人，1994年于武汉大学获得硕士学位，现为韶关学院教授、硕士生导师，主要研究领域为形式语义学，可靠性软件等。

Indexed Co-inductive Data Type Based on Fibrations Theory in Programmingƽ

MIAO Decheng1+,XI Jianqing2,DAI Jingguo1
1.School of Information Science and Engineering,Shaoguan University,Shaoguan,Guangdong 512005,China
2.School of Software,South China University of Technology,Guangzhou 510640,China

E-mail:tony10860@126.com

Traditional methods including category theory and coalgebra have some drawbacks to analyze semantic behavior and describe co-inductive rule,this paper explores indexed co-inductive data type(ICDT)in programming by Fibrations theory.Firstly,this paper constructs indexed Fibration by change of base,presents some tools such as equation functor and quotient functor of indexed Fibration,and then analyzes deeply semantic behavior of ICDT by adjunction property and lifting equation-preserving.Based on this,this paper proposes a parameterized co-recursive operation on ICDT to describe abstractly co-inductive rule with universality in the framework of Fibrations theory, also briefly introduces applications of Fibrations theory for ICDT by example.Compared with traditional methods, brief descriptions and flexible expansibility of Fibrations theory can analyze semantic behavior of ICDT accurately, its superior abstractness doesnƳt rely on particular computing environments to describe co-inductive rule with universality of ICDT.

semantic behavior;co-induction rule;change of base;lifting;co-recursion

2015-08,Accepted 2015-10.

10.3778/j.issn.1673-9418.1508047

A

TP301.2

*The National Natural Science Foundation of China under Grant No.61103038(国家自然科学基金);the Natural Science Foundation of Guangdong Province under Grant No.S2013010015944(广东省自然科学基金);the High School Outstanding Young Teacher Training Plan Foundation of Guangdong Province under Grant No.YQ2014155(广东省高等学校优秀青年教师培养计划).

CNKI网络优先出版:2015-11-11,http://www.cnki.net/kcms/detail/11.5602.TP.20151111.1644.002.html

MIAO Decheng,XI Jianqing,DAI Jingguo.Indexed co-inductive data type based on Fibrations theory in programming.Journal of Frontiers of Computer Science and Technology,2016,10(10)：1482-1492.