混合迁移的高效BBO算法及其在图像分割中的应用*
张新明,涂 强,尹欣欣
1.河南师范大学 计算机与信息工程学院,河南 新乡 453007
2.河南省高校计算智能与数据挖掘工程技术研究中心,河南 新乡 453007
混合迁移的高效BBO算法及其在图像分割中的应用*
张新明1,2+,涂强1,尹欣欣1
1.河南师范大学 计算机与信息工程学院,河南 新乡 453007
2.河南省高校计算智能与数据挖掘工程技术研究中心,河南 新乡 453007
针对高维多阈值分割由于维数增加带来的优化难度加大的问题以及标准生物地理学优化(biogeographybased optimization,BBO)算法效率不高的问题,提出了一种用于高维OTSU多阈值分割的高效生物地理学优化(efficient BBO,EBBO)算法。首先构建新型随机扰动变异算子,然后将此变异算子融合到启发式迁移算子中形成一种高性能的混合迁移算子,去掉了计算变异概率和设置变异参数等环节,以便提高算法的效率;其次将基于迁出率的赌轮选择方式改成无需迁出率的榜样学习选择方案,并将迁入率的多次计算变成一次计算,进一步提高算法的效率;然后将BBO算法中的精英保留方案换成贪婪选择方法,以加快算法的收敛速度;最后将这种EBBO算法应用到高维OTSU多阈值分割中。实验结果表明,与当前的EBO算法、BDE算法、MKTO算法以及BBO算法相比,EBBO算法在高维多阈值分割中不仅有更好的优化性能和更快的运行速度,而且减少了参数设置。
智能优化算法;生物地理学优化算法;图像分割;多阈值分割;最大类间方差法
1 引言
生物地理学优化(biogeography-based optimization,BBO)算法是Simon在2008年提出的一种新颖的群智能进化算法[1]。由于其优化性能优良,稳定性好,在诸多领域得到了广泛的应用[2-7]。BBO算法通过其独特的迁移算子实现候选解之间的信息共享,改善较差的候选解;通过随机变异算子增加种群的多样性。然而,其迁移算子是通过候选解之间的特征值替换实现的,由于受候选解的限制,该算法易陷入局部最优,而且随机变异算子会影响算法的收敛速度。
为了提高BBO算法的优化性能,许多学者进行了大量的研究。Ma和Simon提出了一种混合的迁移算子,通过从两个父代个体中选取特征加以不同权重来产生一个新的子代特征,并将这种算法应用于约束优化问题[5];Ma等人提出了3种新的BBO算法,分别为完全迁入BBO、完全迁出BBO、部分迁出BBO,并通过马尔科夫链进行理论分析[8];Guo等人对迁移模型进行深入理论分析[9];Simon等人通过不断重初始化和局部搜索提出了一种改进的BBO算法,提高了优化性能[10]。
阈值分割是常用的图像分割方法之一,简单有效,其关键是选取合适的阈值。常用的阈值法有OTSU法[11]、最小交叉熵法[12]和最大熵法[13]等。OTSU法根据图像的一维灰度直方图选取阈值,以目标和背景之间方差最大为选取准则,是一种简单的自动阈值选取方法[11]。然而,随着选取阈值数量的增加,其计算复杂度也随之成指数倍增加。因此,需要引入智能优化算法对阈值搜索过程进行优化。文献[12-14]分别将萤火虫优化算法、分子动理论优化算法和改进的差分进化算法应用到基于交叉熵、最大熵和最大类间方差的多阈值分割中,极大提高了多阈值分割的速度。但这些基于智能优化算法的多阈值分割方法都仅限于讨论2至5阈值分割问题,而对于5阈值以上的高维多阈值分割问题几乎未作讨论。而实际应用中,存在大量的高维多阈值分割问题。由于高维优化难度增大,对于智能优化算法是一种挑战。
本文针对BBO算法存在的不足和高维OTSU的图像多阈值分割问题,提出了一种高效的BBO(efficient BBO,EBBO)算法,简化了算法的优化流程,提升了算法的计算效率。高维多阈值分割实验证明,EBBO算法不仅有较好的优化性能,而且需调整的参数更少,易于操控。
2 基本BBO算法
在BBO算法[1]中,一个栖息地相当于一个候选解,其适宜度向量(suitability index variable,SIV)相当于解个体中的特征向量。用栖息适宜指数(habitat suitability index,HSI)衡量栖息地是否适合于种群生存,即用来评估解个体的优劣。优质解的HSI值高,相当于栖息地适宜指数高,物种种类丰富;当趋于饱和时,物种会迁出到相邻的栖息地。相反,低HSI解倾向于接受来自高HSI解的特征值。栖息地之间通过迁移和变异进行候选解之间的信息交换,改善栖息地的HSI。迁移操作通过分享栖息适宜指数较高栖息地的特征值来改变栖息适宜指数较低栖息地的SIV。迁移操作表示如下:

其中,Hi是准备迁入的栖息地;He是准备迁出的栖息地。
迁移算子如算法1所示。在算法1中,λi为迁入率,μi为迁出率,计算方式如式(2)所示:
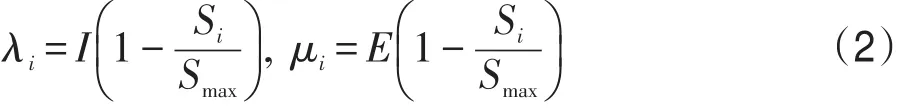
其中,I、E分别表示最大迁入率和最大迁出率;Si表示当前种群数量;Smax表示最大种群数量。
算法1迁移算子

BBO算法通过变异算子模拟栖息地环境突变造成的物种数量的变化,提高探索能力,其变异算子见算法2。
算法2变异算子

栖息地变异概率mi与其物种数量概率成反比。变异概率计算公式表示如下:

其中,mmax表示最大变异概率,是自定义参数;Pmax= max(Pi),Pi表示栖息地的物种概率,定义如下:
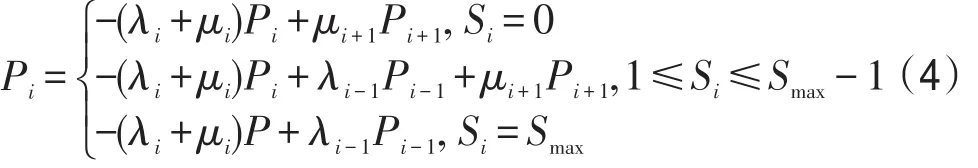
基本BBO算法的流程如图1所示。
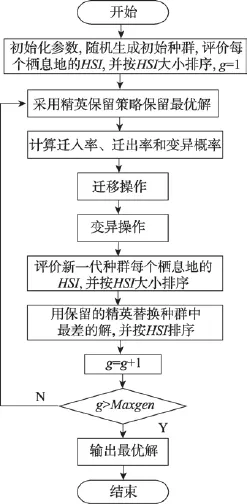
Fig.1 Flow chart of BBO图1 基本BBO算法流程图
3 高效BBO算法
虽然BBO算法有许多优势,但是分析BBO算法发现有如下不足:(1)通过迁移算子实现候选解之间的信息共享,用较优解中的特征值替换适应度较差解的特征值,受候选解的限制,这种替换方式容易陷入局部最优。(2)通过随机变异算子增加了种群多样性,但是这种随机突变的变异操作会破坏优质解,导致算法收敛速度慢。(3)原算法采用精英保留策略需要在每次迭代对种群进行两次排序,如此排序增加了计算复杂度。(4)需要精心调整参数获得最佳性能,如调整最大变异概率等参数。(5)迁移算子中采用赌轮法选择栖息地,该方法在种群数量少的情况下不合适,并且计算复杂度较高。(6)每次迭代都需要计算式(2)至式(4)来获得迁入率、迁出率和变异概率,如此也增加了计算复杂度。为了克服基本BBO算法的不足,提高其优化性能,加快收敛速度,本文提出了一种基于新型混合迁移算子的高效BBO算法。新型混合迁移算子由微扰动的启发交叉算子和随机扰动算子组成。
3.1微扰动的启发式交叉算子
BBO算法中基于随机突变的变异算子无法控制其变异幅度,尤其在后期有可能会破坏较好的解,影响算法的收敛速度。本文提出了一种启发式交叉与微扰动结合的算子:首先丢弃原来的变异操作,然后构建启发式交叉算子,最后在此基础上添加一个微扰动变异因子,其表达式如下:
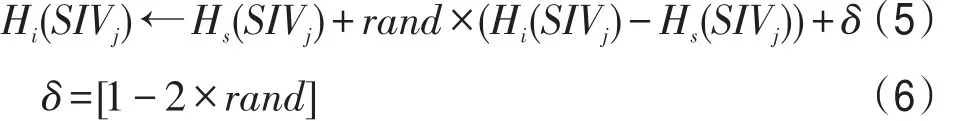
其中,Hi是被选中进行迁移操作的候选解;Hs是通过迁出率选出的较好解;SIVj表示该候选解中进行迁移操作的特征值(j=1,2,…,d,d为特征数);rand为0到1之间的随机数;δ为扰动因子;[]为四舍五入取整运算。从式(6)可以看出,δ的取值为0、-1和1三种情况。当δ=0时,不作扰动,仅启发交叉算子起作用,否则在启发交叉的基础上作-1或者1的微小扰动,因为阈值变化的最小单位为1个灰度级。通过这种微扰动操作能够加快收敛速度,并提高解的精度。从式(5)可以看出,启发式交叉算子不仅保持了原算法差解共享优解特征值的结构,而且增加了搜索空间,提高了搜索能力。另外,无参数需要设置和调整,提高了算法可操作性。
3.2榜样学习选择方案
原算法中通过迁出率采用赌轮选择方法挑选出较优解,但在赌轮选择中,当群体规模不大时,产生的随机数可能并不代表其随机变量的真正分布情况。因此,在选择时并不能选择出较好的解,且赌轮选择方法比较耗时。因此本文提出了一种简单可行的榜样选择方案,将原迁移算子中选择迁出候选解的赌轮选择方法改为榜样选择法。所谓榜样选择法,就是从较优的群体中随机挑选出个体,供相对较差的个体学习。在BBO算法中,每次迭代后都按照适应度大小进行排序,也就是说排在前面的个体一定比后面的个体优秀,是后面个体的学习榜样。因此榜样选择方案如式(7)所示:

其中,s表示选中将要进行迁出操作的候选解序号;i表示第i个候选解;éù为向上取整运算。式(7)表示从第i个候选解之前的i-1个候选解中随机选取一个进行特征值迁出,前i-1个候选解一定优于第i个候选解,是第i个候选解的学习榜样。从式(7)可以看出,榜样选择方案不仅克服了赌轮选择法的不足,且无需计算迁出率,降低了计算复杂度。
3.3随机扰动算子
对于候选解中没有选中进行迁移操作的特征值,添加一个随机扰动因子,以此增加种群的多样性,提高全局搜索能力,随机扰动因子表示如下:

其中,Hi(SIVj)表示该候选解中未被选中进行迁移操作的特征值;Hbest为当前最优解;Hm和Hn是随机选择的两个候选解,满足m,n,i∈[1,N],N为种群总数,且m、n和i互不相等。由式(8)可知,扰动幅度受控于随机数rand,这不仅提高了算法探索能力,而且也不用设置和调整扰动幅度参数。混合迁移算子见算法3,这种算子具备良好的开采能力和探索能力,同时省去了原算法参数设置,简化了计算过程,大幅降低了计算复杂度。
算法3混合迁移算子

另外,为了进一步降低计算复杂度,首先将标准BBO算法中计算迁入率的步骤放到种群更新迭代循环之前。因为在保证种群的适应度值总为有效值的情况下,可以将迁入率的计算放到循环之外,不影响算法的准确性,避免了重复计算造成的浪费。其次,将标准BBO算法中的精英保留策略改为贪婪选择方案。将经过融合变异的迁移操作后产生的新一代解集与上一代解集进行比较,采用优胜劣汰原则保留较优的候选解。这样不仅减少了精英参数的设置,而且减少了一次排序操作,提高了算法的运算效率。EBBO算法的流程图如图2所示。
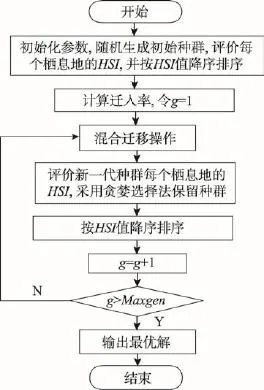
Fig.2 Flow chart of EBBO图2 EBBO算法流程图
4 基于高效BBO算法的图像多阈值分割
4.1OTSU法多阈值选择
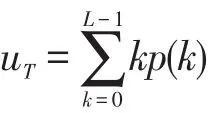
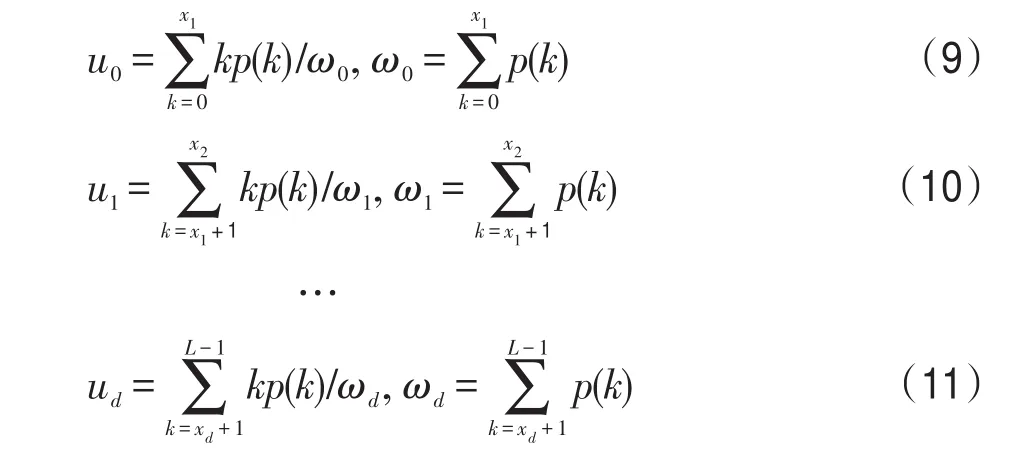
类间方差表示为:
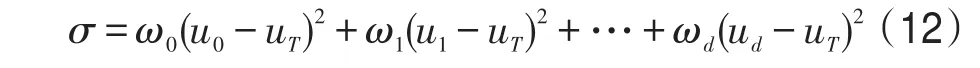
使σ值最大的一组值即为OTSU法的最佳阈值组合。
4.2基于EBBO算法的OTSU多阈值分割
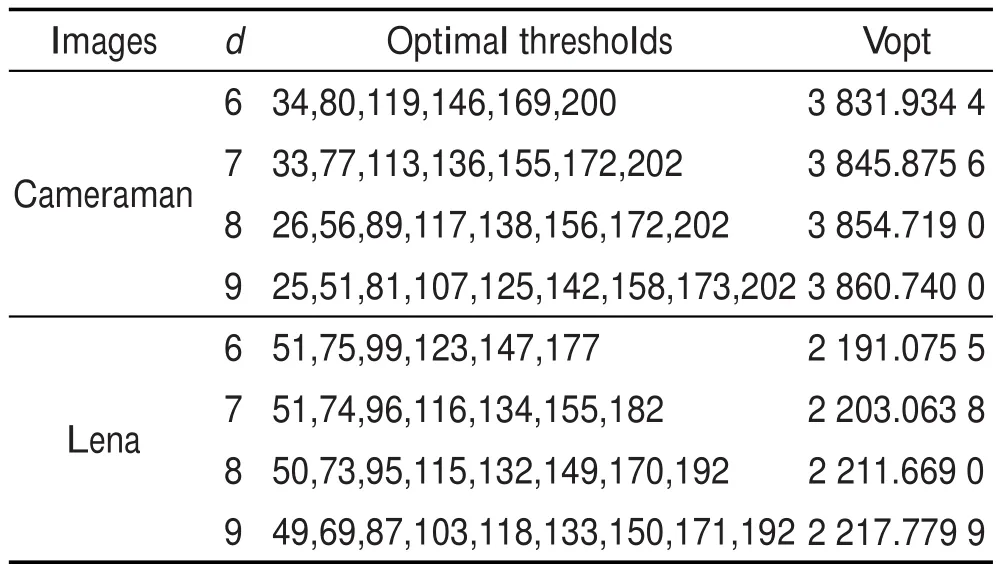
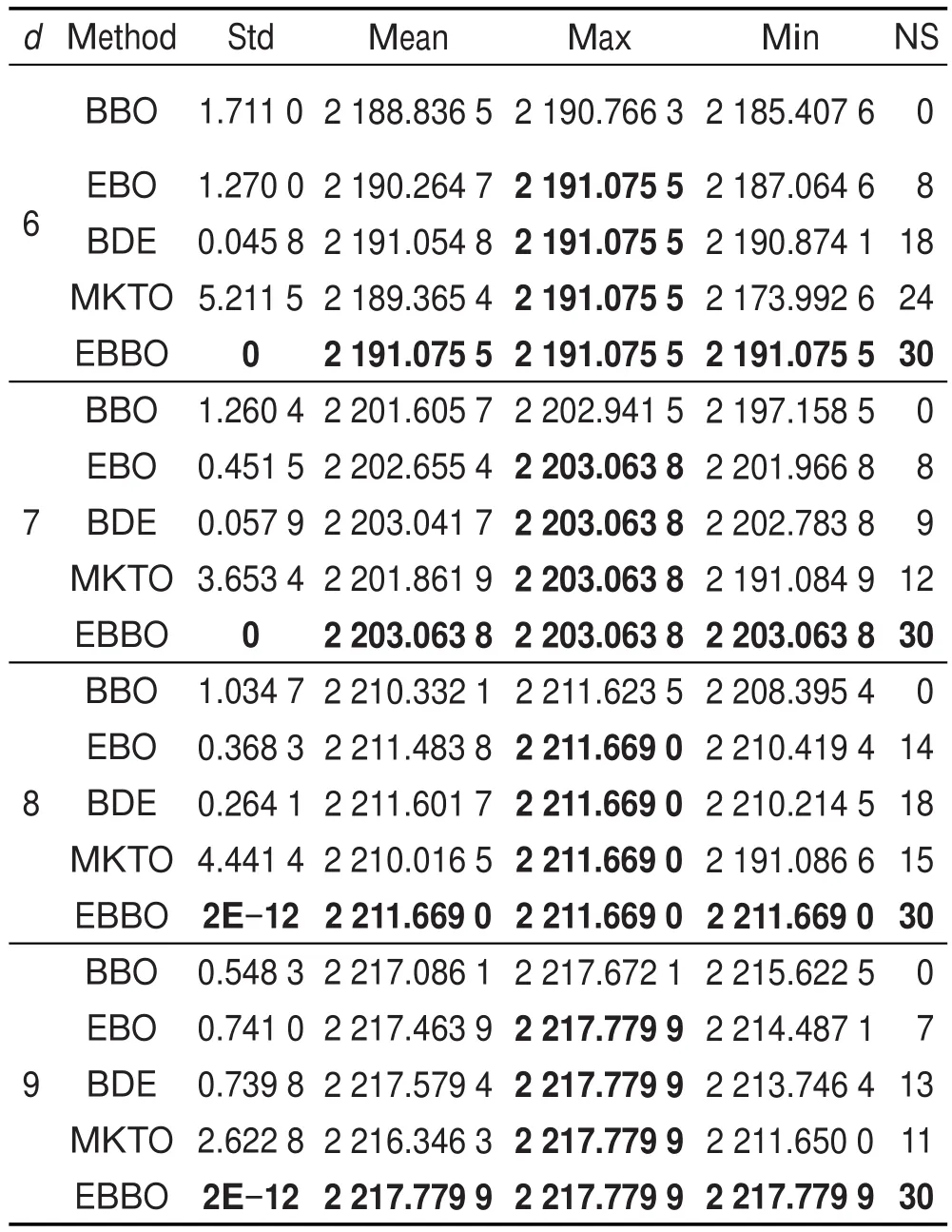
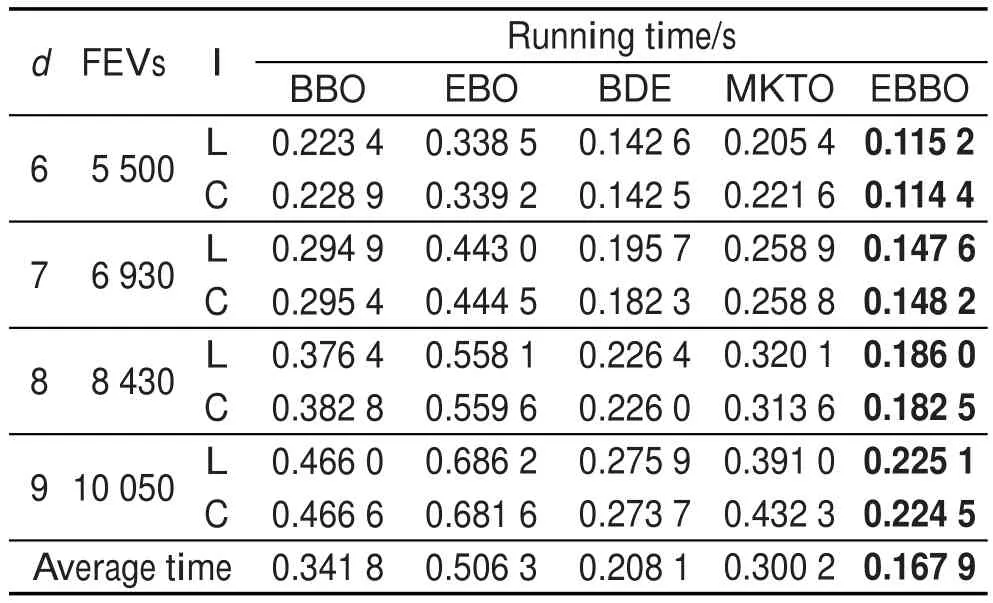
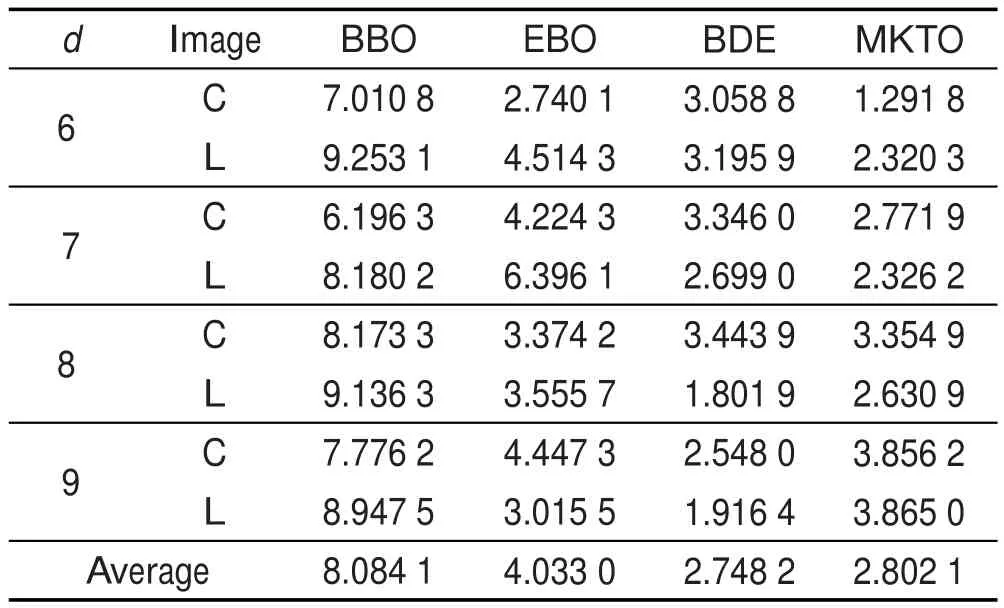
假设对图像d阈值分割,则解向量为x=[x1,x2,…, xd],其取值为正整数并且满足0 步骤1读入图片,初始化参数。设最大迭代次数为Maxgen,种群数量为N,阈值个数为d。 步骤2随机生成初始化种群X,X为N行d列正整数矩阵,将种群X中的每个解按从小到大顺序排序,以满足阈值向量的要求;用式(12)评估每个栖息地Xi(i=1,2,…,N)的HSI,按照HSI值的降序对Xi进行排序。 步骤3根据式(1)计算迁入率。 步骤4执行融合了变异的迁移操作。 步骤5用式(12)评估每个新解Xi(i=1,2,…,N)的HSI,并执行贪婪选择算子,保留新一代解中较优解。 步骤6按照HSI值的降序对Xi排序。 步骤7若没有达到停止准则,转到步骤4,否则,停止循环,得到最优阈值向量。 步骤8用求得的最优阈值向量进行图像分割,输出分割后的图像。 为了检验基于EBBO算法的最大类间方差多阈值分割方法的有效性,进行图像多阈值分割实验,并将其实验结果与基于基本BBO算法[1]、EBO(ecogeography-based optimization)算法[3]、BDE(beta differential evolution)算法[11]和MKTO(molecular kinetic theory optimization)算法[13]的最大类间方差多阈值分割结果进行比较。其中EBO是改进的生物地理学算法,BDE是改进的差分进化算法,MKTO是近年提出的一种分子动理论优化算法,具有较强的优化竞争力。由于篇幅限制,本文仅用Cameraman.png(256×256像素)和Lena.jpg(512×512像素)两幅图片作为示例进行说明,见图3所示。其多阈值分割结果见图4和图5所示。其中为了提高视觉效果,本文采用假彩色表示分割结果,不同的颜色代表不同的分割区域。所有实验均在操作系统为Windows 7,CPU为主频3.10 GHz和内存为4 GB的PC上进行,编程语言采用Matlab R2014a。为了公平起见,5种算法的种群大小N都设为30,它们的最大迭代次数(Maxgen)设置也相同,并使Maxgen随着阈值的增加而增加,以便达到自动调整Maxgen的目的:Maxgen=2d2+ 20(d-1)+12。BBO算法、EBO算法、BDE算法和MKTO算法的其他参数设置见相应的文献,而EBBO算法的其他参数仅需要设置最大迁入率I,I同样设置为1。 Fig.3 Original images图3 原图像 Fig.4 Multilevel thresholded results of Cameraman image图4 Cameraman图像的多阈值分割结果 Fig.5 Multilevel thresholded results of Lena image图5 Lena图像的多阈值分割结果 5.1优化性能比较 为了凸显EBBO算法的优化性能,本文仅仅考察其在高维多阈值搜索中的优化情况,不讨论5种算法在图像的2到5阈值低维问题中的优化性能,仅对6到9阈值高维情况进行讨论和分析。将5种优化算法用于两幅图像的多阈值搜索中,并独立运行30次,选30次中的最大值Max(最好值)、平均值Mean、方差Std、最小值Min(最差值)及算法的成功次数(numbers of success,NS)作为评价标准来考察它们的优化性能。其中,一种算法的成功次数是以Vopt作为成功的评价参考,即独立运行30次中该算法寻找的最优值为Vopt的次数;而Vopt为5种算法在同一图像、同一阈值上共运行30×5次中搜索到的最大类间方差值,即5种算法分别运行30次共同搜寻到的最优点对应的类间方差值。Vopt及其对应的最优阈值组合见表1所示。表2和表3分别列出了5种算法在Cameraman和Lena上阈值搜索的优化结果,其中加黑的值均为优者。从表2和表3中可以看出,EBBO算法获得了最好的优化性能,不管是Cameraman图像,还是Lena图像,都能搜索到最优阈值向量,6、7、8和9这4种阈值搜索的成功次数都为30,即成功率为100%,大幅度领先于BBO算法。这是由于EBBO算法采用随机变异增加种群的多样性,提高了算法全局搜索能力,采用启发式交叉和微扰动,增强了局部搜索能力和收敛速度。优化性能其次的是MKTO算法,再其次是BDE算法,最差是BBO算法。这说明本文提出的高效BBO算法是有效的。 Table 1 Maximum variance values and their optimal thresholds of two images表1 两幅图像的最大类间方差值和其对应的最优阈值组合 Table 2 Result comparison among 5 optimization algorithms on Cameraman image segmentation表2 5种优化算法对Cameraman图像阈值搜索结果 Table 3 Result comparison among 5 optimization algorithms on Lena image segmentation表3 5种优化算法对Lena图像阈值搜索结果 5.2运行时间和收敛速度比较 表4是5种优化算法在两幅图像不同的阈值搜索中的耗时,其中C和L分别表示Cameraman图像和Lena图像,FEVs表示目标函数运行的次数。图6(a)、图6(b)分别是5种算法在Cameraman图像8阈值和9阈值搜索的收敛图。从表4中可以看出,与BBO算法相比,EBBO的运行时间少,约为BBO的一半,这是由于它采用榜样选择方法、贪婪选择方案等一系列的改进措施降低了计算复杂度。EBBO算法也是5种算法里运行时间最少的算法,见表4的最后一列,大约是EBO的25%,其次是BDE算法,再其次是MKTO算法,EBO算法耗费的时间最多,这是因为EBO算法中有两次赌轮选择等计算。将表4与表2和表3结合起来分析,在同样的FEVs情况下,EBBO算法能够找到最优解,成功率高,这说明本文算法收敛速度快。从图6的收敛图也印证了此结论。 Table 4 Running time comparison among 5 optimization algorithms表4 5种优化算法运行时间对比 5.3t-test测试比较 t-test是一种用于区分两种算法优劣的统计方法,如果t值为正,则表示算法1的寻优性能优于算法2,反之,则算法2的寻优性能优于算法1。计算公式为: 式(13)中,α1、α2分别表示算法1与算法2的平均适应度值;σ1、σ2分别表示算法1与算法2的标准方差;ε表示自由度,本文ε=49。从数理统计t分布表可知,t>0表明算法1要优于算法2,t=0表明算法1与算法2的性能相等,t=1.645表明算法1性能优于算法2,且具有95%的置信度,t=2.060表明算法1性能优于算法2,且具有98%的置信度。表5是EBBO与BBO、EBO、BDE和MKTO优化算法的t-test值。 Table 5 t-test value comparison of EBBO between 4 other algorithms表5 EBBO与其他4种优化算法t-test比较 Fig.6 Convergence graphs of 5 optimization algorithms on Cameraman image图6 5种优化算法在Cameraman图像上的收敛曲线图 从表5可以看出,在两幅图像的6至9阈值搜索中,EBBO算法与其他4种优化算法的大部分t-test值高于2.060,表明两算法区分度具有98%的置信水平。 综上所述,在基于OTSU的图像多阈值分割中,EBBO算法能快速收敛到全局最优值,稳定性优良,全局和局部搜索能力较好。 本文提出了一种高效生物地理学算法,将变异算子融合到迁移算子中,简化了算法优化流程;采用榜样选择方案和贪婪保留法进一步降低了算法的计算复杂度。最后将EBBO算法应用到基于OTSU的图像多阈值分割中,实验结果表明,基于高效生物地理学算法的图像多阈值分割法分割速度快,稳定性好,能够取得全局最优值,而且可操作性更强。另外EBBO算法可以推广到其他优化问题中[15-16]。 [1]Simon D.Biogeography-based optimization[J].IEEE Transactions on Evolutionary Computation,2008,2(6):702-713. [2]Xiong Guojiang,Shi Dongyuan.An improved analytic model for fault diagnosis of power grids and its self-adaptive biogeography-based optimization method[J].Transactions of China Electrotechnical Society,2014,29(4):205-211. [3]Zheng Yujun,Ling Haifeng,Xue Jinyun.Ecogeographybased optimization:enhancing biogeography-based optimization with ecogeographic barriers and differentiations[J]. Computers&Operations Research,2014,50(5):115-127. [4]Bi Xiaojun,Wang Jue,Li Bo,et al.An εconstrained biogeography-based optimization with dynamic migration[J].Journal of Computer Research and Development,2014,51(3): 580-589. [5]Ma Haiping,Simon D.Blended biogeography-based optimization for constrained optimization[J].Engineering Applications ofArtificial Intelligence,2011,24(3):517-525. [6]Ding Zhiguo,Fei Minrui,Ma Haiping.Ensemble selection method based on biogeography-based optimization algorithm [J].Journal of System Simulation,2014,26(5):996-999. [7]Zheng Zhaobao.Application of biogeography-based optimization to image segmentation[J].Geomatics and Information Science of Wuhan University,2011,36(8):932-935. [8]Ma Haiping,Simon D,Fei Minrui,et al.Variations of biogeography-based optimization and Markov analysis[J].Information Sciences,2013,220:492-506. [9]Guo WeiƳan,Wang Lei,Wu Qidi.An analysis of the migration rates for biogeography-based optimization[J].Information Sciences,2014,254:111-140. [10]Simon D,Omran M G H,Clerc M.Linearized biogeographybased optimization with re-initialization and local search [J].Information Sciences,2014,267:140-157. [11]Zhang Xinming,Sun Yinjie,Zheng Yanbin.Precise twodimensional Otsu’s image segmentation and its fast recursive realization[J].Acta Electronica Sinica,2011,39(8): 1778-1784. [12]Horng M H,Liou R J.Multilevel minimum cross entropy threshold selection based on the firefly algorithm[J].Expert Systems withApplication,2011,38(12):14805-14811. [13]Fan Chaodong,Ouyang Honglin,Zhang Yingjie,et al.Optimal multilevel thresholding using molecular kinetic theory optimization algorithm[J].Applied Mathematics and Computation,2014,239:391-408. [14]Ayala H V H,dos Santos F M,Mariani V C,et al.Image thresholding segmentation based on a novel beta differential evolution approach[J].Expert Systems with Application,2015,42(2):2136-2142. [15]Zhang Xinming,Feng Mengqing,Yin Xinxin,et al.Hybrid chaotic artificial bee colony algorithm based on simplex search for low-dimensional function optimization[J].Journal of Chinese Computer Systems,2014,35(12):2738-2744. [16]Zhang Xinming,Zheng Yanbin,Zhang Huiyun.Image segmentation based on combining chaos and multiobjective programming theory[J].Journal of Chinese Computer Systems,2010,31(7):1416-1420. 附中文参考文献: [2]熊国江,石东源.电网故障诊断改进解析模型及其自适应生物地理学优化方法[J].电工技术学报,2014,29(4):205-211. [4]毕晓君,王珏,李博,等.基于动态迁移的约束生物地理学优化算法[J].计算机研究与发展,2014,51(3):580-589. [6]丁智国,费敏锐,马海平.一种基于生物地理学优化算法的集成选择方法[J].系统仿真学报,2014,26(5):996-999. [7]郑肇葆.生物地理学优化(BBO)在图像分割中的应用[J].武汉大学学报:信息科学版,2011,36(8):932-935. [11]张新明,孙印杰,郑延斌.二维直方图准分的Otsu图像分割及其快速实现[J].电子学报,2011,39(8):1778-1784. [15]张新明,冯梦清,尹欣欣,等.混沌蜂群与单纯形搜索融合的低维复杂函数优化[J].小型微型计算机系统,2014,35 (12):2738-2744. [16]张新明,郑延斌,张慧云.应用混沌多目标规划理论融合的图像分割[J].小型微型计算机系统,2010,31(7):1416-1420. ZHANG Xinming was born in 1963.He is a professor at Henan Normal University,and the member of CCF.His research interests include intelligent optimization algorithm,digital image processing and pattern recognition. 张新明(1963—),男,湖北孝感人,河南师范大学教授,CCF会员,主要研究领域为智能优化算法,数字图像处理,模式识别。 TU Qiang was born in 1995.He is an M.S.candidate at Henan Normal University.His research interests include digital image processing and intelligent optimization algorithm. 涂强(1995—),男,河南光山人,河南师范大学硕士研究生,主要研究领域为数字图像处理,智能优化算法。 YIN Xinxin was born in 1990.She is an M.S.candidate at Henan Normal University.Her research interests include digital image processing and intelligent optimization algorithm. 尹欣欣(1990—),女,河南安阳人,河南师范大学硕士研究生,主要研究领域为数字图像处理,智能优化算法。 Efficient BBO Algorithm Based on Hybrid Migration and Its Application to Image Segmentationƽ ZHANG Xinming1,2+,TU Qiang1,YIN Xinxin1 E-mail:xinmingzhang@126.com In view of more optimization difficulty with higher dimensions in the high-dimensional multilevel thresholding and the low optimization efficiency of biogeography-based optimization(BBO)algorithm,this paper proposes an efficient BBO(EBBO)algorithm applied to high-dimensional OTSU multilevel image thresholding.Firstly,a novel little disturbance mutation operator is taken,and the operator is blended into the heuristic operator to get a new migration operator,which simplifies the processes of the proposed algorithm,such as not computing mutation probability or setting its parameters,in order to improve the efficiency.Secondly,the roulette wheel selection is replaced with the example learning approach and the immigration rate is calculated once before the iteration loop instead of calculating many times in the original algorithm to reduce the computational complexity further.Thirdly, a greedy selection operator is used instead of the original elitist selection operator to accelerate the convergence pro-cess.Finally,the EBBO algorithm is applied to high-dimensional OTSU multilevel image thresholding.The experimental results show that the performance of proposed EBBO is better,faster and more stable than standard BBO, EBO,BDE and MKTO,and there are fewer parameters to be tuned in the EBBO. intelligent optimization algorithm;biogeography-based optimization algorithm;image segmentation; multilevel thresholding;maximal between-cluster variance 2015-08,Accepted 2015-11. 10.3778/j.issn.1673-9418.1508028 A TP18;TP391.41 *The Key Technologies R&D Program of Henan Province of China under Grant No.132102110209(河南省重点科技攻关项目);the Research Program of Application Foundation and Advanced Technology of Henan Province of China under Grant No.142300410295 (河南省基础与前沿技术研究计划项目). CNKI网络优先出版:2015-11-12,http://www.cnki.net/kcms/detail/11.5602.TP.20151112.1513.004.html ZHANG Xinming,TU Qiang,YIN Xinxin.Efficient BBO algorithm based on hybrid migration and its application to image segmentation.Journal of Frontiers of Computer Science and Technology,2016,10(10):1459-1468.5 实验结果与分析




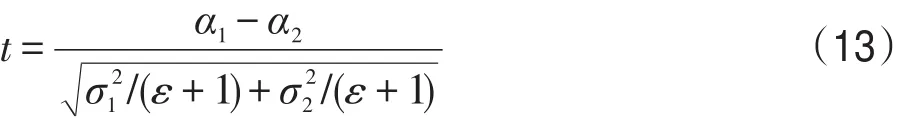

6 结束语



1.College of Computer and Information Engineering,Henan Normal University,Xinxiang,Henan 453007,China
2.Henan Province Engineering Technology Research Center for Computing Intelligence&Data Mining,Xinxiang, Henan 453007,China

