一种基于PH螺线的避障重规划路径修正方法
杨秀霞, 周硙硙, 张毅
(1.海军航空工程学院 控制工程系, 山东 烟台 264001;2.海军航空工程学院 研究生管理大队, 山东 烟台 264001)
一种基于PH螺线的避障重规划路径修正方法
杨秀霞1, 周硙硙2, 张毅1
(1.海军航空工程学院 控制工程系, 山东 烟台 264001;2.海军航空工程学院 研究生管理大队, 山东 烟台 264001)
针对现有避障算法忽略重规划路径侵犯威胁障碍物安全圆的问题,提出了一种基于Pythagorean Hodograph(PH)螺线修正避障重规划路径的方法。该方法能够考虑无人飞行器路径规划的相关性能约束,且较其他路径修正算法复杂度较低、实时性高,能够满足UAV在线规避动静态障碍物的要求。仿真结果验证了该方法的有效性和可行性。
避障; PH螺线; 路径规划; 无人飞行器
0 引言
在未知动态复杂环境下,为确保UAV安全飞行到达目的地,需要对飞行过程中探测到的动静态障碍物进行避碰,因此,规划出满足约束条件安全可飞行的路径是UAV飞行控制技术的重要方面。
近年来,在机器人和无人飞行器领域,众多学者对复杂环境下的避障算法进行了研究,这些算法包括:微分几何法[1]、导引法[2]、势场法[3]、随机搜索算法[4]和曲线规划法[5]等。文献[1]基于微分几何实现了对动静态障碍物的威胁判断和避碰;文献[2]通过导引的方式实现了对探测到的威胁障碍物避碰;文献[3]通过势场中障碍物的斥力和目标点的引力完成了对当前航迹的避障重规划;文献[4]在搜索算法的基础上确定安全航迹点,并对航迹进行平滑完成避障路径重规划;文献[5]基于参数化曲线实现UAV的避障路径重规划。但在这些方法中,忽略了避障重规划路径可能对威胁障碍物安全圆的侵犯问题,且该问题会影响UAV的安全飞行。文献[6]给出了一种解决UAV避障重规划路径侵犯威胁障碍安全圆问题的圆心跟踪算法,算法需要通过迭代的方式确定安全圆上新的航迹点,因此,该算法的实时性较差且较为复杂。
在工程领域内,螺线具有广泛的实际应用,如机器人的路径模拟、道路设计等。Pythagorean Hodograph(PH)螺线具有优良的性质,该曲线的曲率符号保持不变,且曲率大小随螺线参数单调变化。另外,同PH曲线一样,PH螺线弧长可以被精确计算且其等距线具有有理形式。文献[7]将PH螺线应用于平稳加工的路径规划中,实现了高速切削加工平稳的曲线过渡,解决了由于加速度不连续变化导致的数控机床激烈抖动问题。Bass[8]将道路设计中的曲线过渡分为5种情况:直线与直线之间的过渡;直线与圆之间的过渡;圆与圆之间的C型螺线过渡;圆与圆之间的S型螺线过渡;圆与其内部圆弧之间的过渡。由于回旋曲线的曲率和弧长呈线性关系,文献[9]为满足道路工程设计的需求,基于三次C-Bézier螺线实现了不同道路设计情况下的曲线过渡,解决了回旋曲线不适合计算机设计系统的问题。
由于五次PH螺线内部没有尖点和拐点,可选择其为过渡曲线。另外,当沿曲线运动的速度保持恒定时,法向加速度和向心力与曲率大小变化正相关。因此,以五次PH螺线为过渡曲线可有效地避免向心力突变的问题。本文针对避障算法中未考虑避障重规划路径侵犯威胁障碍物安全圆的问题,提出了一种基于PH螺线的避障路径修正方法。
1 PH螺线路径的构造
1.1五次PH曲线路径规划
本文采用五次PH螺线路径对存在侵犯威胁障碍物安全圆的避障路径进行修正,五次PH螺线路径的构造是基于五次PH路径。
在初始点Ps(xs,ys,φs)和终止点Pf(xf,yf,φf)之间生成的满足约束条件的可飞行路径可表示为:

二维五次PH路径r(t)以控制点的形式可表示为:
(1)
且x(t)和y(t)满足:
(2)
(3)
其中:
(4)
(5)
另外,五次PH路径的6个路径控制点Pk(k=0,1,2,3,4,5)之间存在下列关系:
(6)
P2=P1+0.2(u0u1-v0v1)T+0.2(u0v1+u1v0)N
(7)
(4u1v1+u0v2+u2v0)N/15
(8)
P4=P3+0.2(u1u2-v1v2)T+0.2(u1v2+u2v1)N
(9)
(10)
那么,根据规划五次PH路径的初始化条件和6个控制点之间的关系式,可确定五次PH路径的6个控制点。因此,由式(1)可实现UAV五次PH路径规划。
另外,五次PH路径的曲率表达式为:
(11)
为使规划UAV的路径可飞行,规划的PH路径需满足曲率约束条件,文献[5]给出了生成满足曲率约束条件路径的控制参数选取策略。本文在此基础上构造满足约束条件的五次PH螺线路径,对存在侵犯威胁障碍物安全圆的重规划路径进行修正。
1.2五次PH螺线路径生成
五次PH曲线路径的规划是基于相应的初始化条件,对式(4)和式(5)中的二次多项式u(t)和v(t)系数进行求解。在五次PH曲线路径的基础上,需要对二次多项式u(t)和v(t)中的系数进行定义,使得构造的五次PH路径的曲率满足螺线路径曲率要求,从而实现五次PH螺线路径的规划。
设定:
(12)
(13)
(14)
(15)
因此,对起始点P0(Ps)、终止点P5(Pf)以及终止点P5处的切向量和曲率半径R进行初始化,可以确定在设定条件下的五次PH路径,且关于该五次PH路径的曲率有以下结论:在设定条件下,五次PH路径r(t)的曲率κ(t)具有下列性质:
称具有上述性质的五次PH路径为螺线路径。
2 重规划路径侵犯安全圆问题
2.1侵犯安全圆问题
在复杂环境下执行飞行任务的UAV,当自身携带的传感器装置探测到来自未知动态环境中的动/静态障碍物时,可利用相应的避障算法重规划当前的航迹,实现对威胁障碍物的避碰。通常,避障路径重规划需要在UAV的当前时刻位置坐标Pt、避障点Qavo和目标点P5之间分别生成可飞行的安全路径。但在规划Qavo和P5之间的路径时,由于存在目标点位于威胁障碍物盲区内的情况,则可能存在着重规划路径侵犯威胁障碍物安全圆的问题。避障点和目标点之间的避障重规划路径侵犯威胁障碍物安全圆的情况如图1所示。
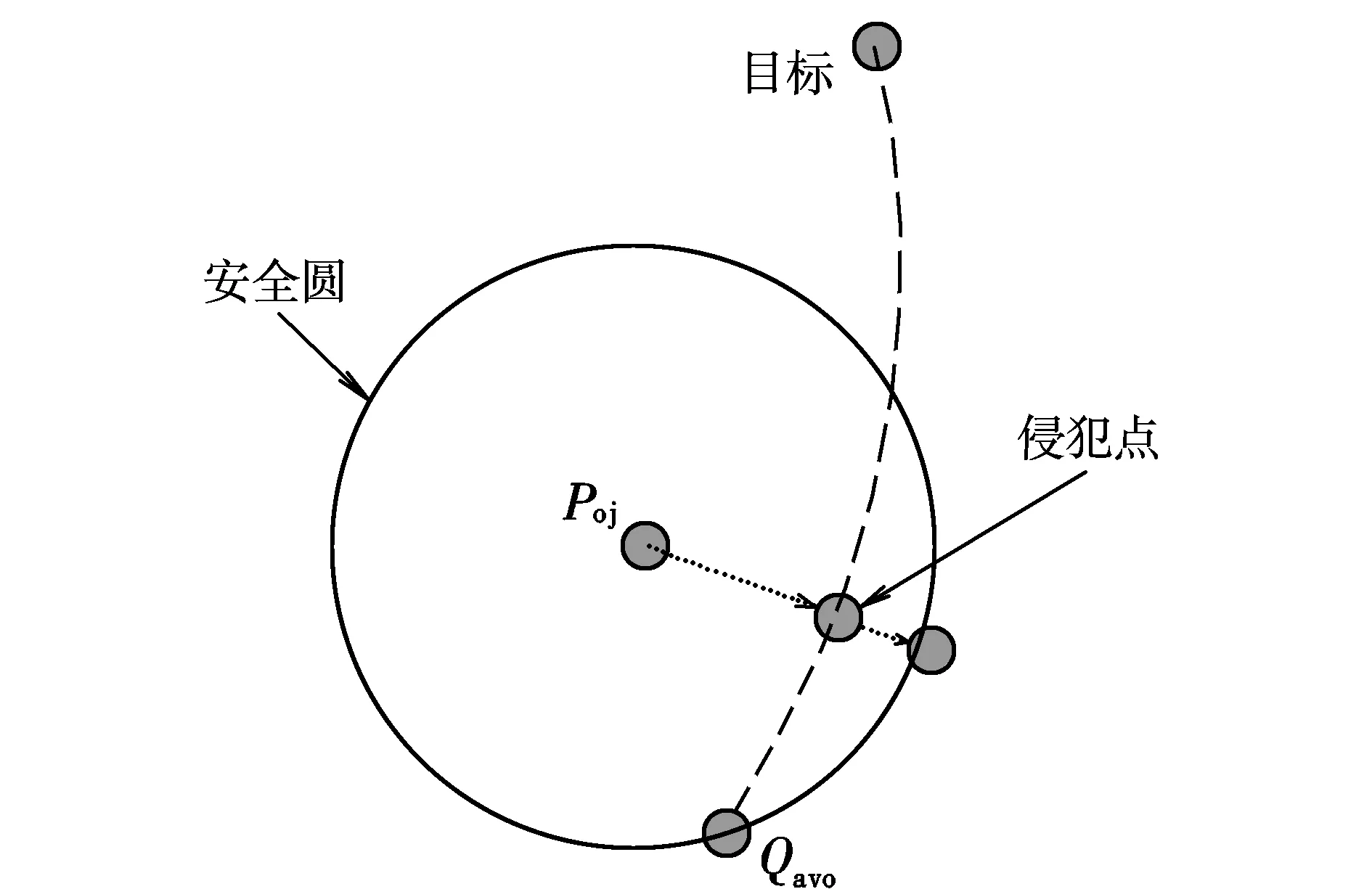
图1 UAV重规划路径侵犯威胁障碍安全圆示意图Fig.1 The sketch that re-planning path of UAV violating threatening obstacle safety circle
关于避障重规划路径侵犯威胁障碍物安全圆问题研究的文献较少,很多威胁障碍物避障算法忽略了该问题,从而降低了避障重规划路径的安全性。文献[2]针对三维情况下的避障重规划路径侵犯主体障碍物安全球问题,提出了一种球心跟踪算法。该算法通过确定一个球面上的虚拟目标点,UAV沿球面飞行到虚拟目标点,直到重新规划的航迹不在侵犯主体障碍物的安全球。但该算法需要不断地迭代,使得重规划的避障路径与主体障碍物的安全球没有交点,从而导致算法较为复杂,使得算法的实时性和可实现性降低。
2.2解决方案
2.2.1二维平面圆心跟踪算法
采用类似三维空间球心跟踪算法[2]的二维平面圆心跟踪算法解决威胁障碍物安全圆侵犯问题,其示意图如图2所示。
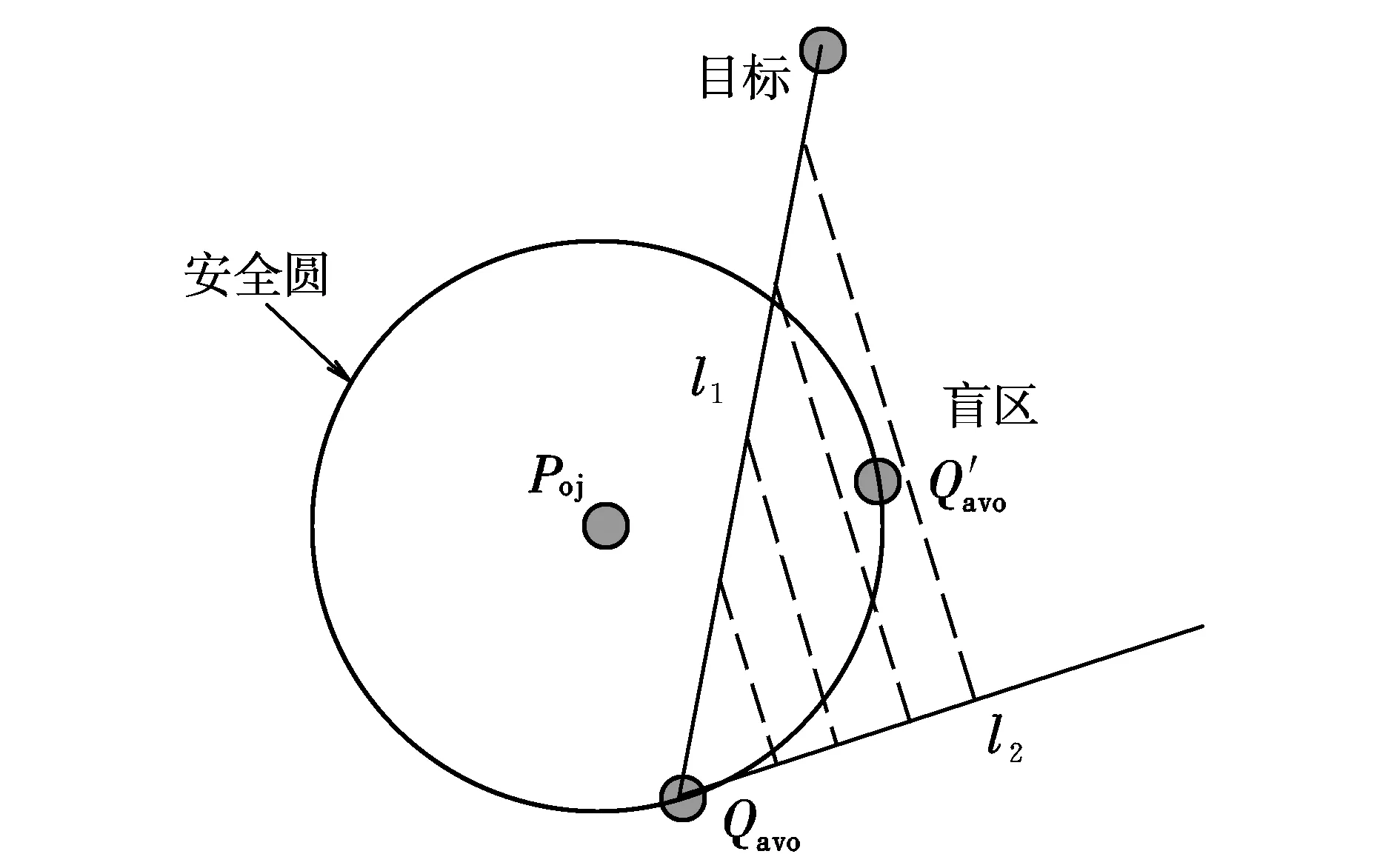
图2 圆心跟踪算法示意图Fig.2 The sketch of center-tracking algorithm
2.2.2安全系数法
在避障算法中,通常将UAV看作质点,并根据UAV与障碍物之间的相对大小将障碍物“膨化”为圆。为解决避障重规划路径侵犯威胁障碍物安全圆问题,可在安全圆半径上乘上一个安全系数,通过控制安全系数的大小解决安全圆侵犯问题。但安全系数会增加避障重规划路径的长度,使得避障重规划路径更加偏离最优初始可飞行路径,从而满足不了重规划路径偏离原路径小的要求。
2.2.3五次PH螺线路径修正法
五次PH螺线路径内部没有尖点和拐点,且其曲率具有良好的性质。采用五次PH螺线路径对侵犯威胁障碍物安全圆的重规划路径进行修正,计算简单、耗时少,能够满足UAV在线避障路径重规划的实时性要求,且能考虑UAV在避障点和目标点处的方向角约束以及自身的最大曲率半径等约束。因此,基于五次PH螺线的避障路径修正方法比二维平面圆心跟踪算法和安全系数法更具优势。为此,本文采用五次PH螺线路径解决UAV在避障点和目标点之间的重规划路径侵犯威胁障碍物安全圆的问题。
3 基于PH螺线的避障路径修正
本文将数学上利用五次PH螺线连接直线与圆的过渡方法应用到UAV避障路径的修正,有效地解决了UAV在避障点和目标点之间重规划路径侵犯主体障碍物安全圆问题,且修正算法避免了其他方法计算复杂、耗时多等问题。与此同时,也考虑了UAV避障路径重规划的性能约束。
3.1规划PH螺线路径
由式(6)~式(10),可确定起始点P0和终止点P5之间的关系为:
(16)
由式(16)可得:
(17)
又因为终止点P5位于障碍物的安全圆上,则:
(18)
式中:h为障碍物安全圆圆心到坐标轴T的距离。
根据式(17)和式(18),并令γ=cosφf可得:
f(γ)=18Rγ2+(11R-60h)γ+91R-60h
(19)
对安全圆半径R和h进行初始化,使得多项式方程f(γ)=0存在解。将该解代入式(6)~式(10)和式(1),即可确定PH螺线路径。
3.2PH螺线路径的调整
由3.1节可规划出初始连接威胁障碍物安全圆的PH螺线路径。为使UAV的整个避障重规划路径曲率连续,需要确保在避障点处的曲率连续。因此,通过PH螺线路径起始点处与避障点处速度矢量方向角的差值,基于相应的变换矩阵,可确保在避障点处的曲率连续。另外,PH螺线路径的起始点可通过坐标平移的方法平移到UAV的实际避障点处。
假设PH路线路径起始点处与避障点处速度矢量方向角的差值为δ,则相应的变换矩阵为:

再通过安全圆的圆心平移重合,可实现PH螺线路径的起始点与避障点重合,且速度矢量的方向角也重合,从而实现对避障重规划路径的修正,解决避障重规划路径侵犯威胁障碍物安全圆问题。此时,PH螺线路径的终止点为设定的虚拟目标点,在虚拟目标点与目标点处的路径重规划可通过文献[5]的方法实现。
4 仿真验证
在避障路径修正过程中,避障点与虚拟目标点之间存在顺时针旋转和逆时针旋转两种位置关系。顺时针旋转位置关系如图3所示,图4为PH螺线路径的曲率变化。
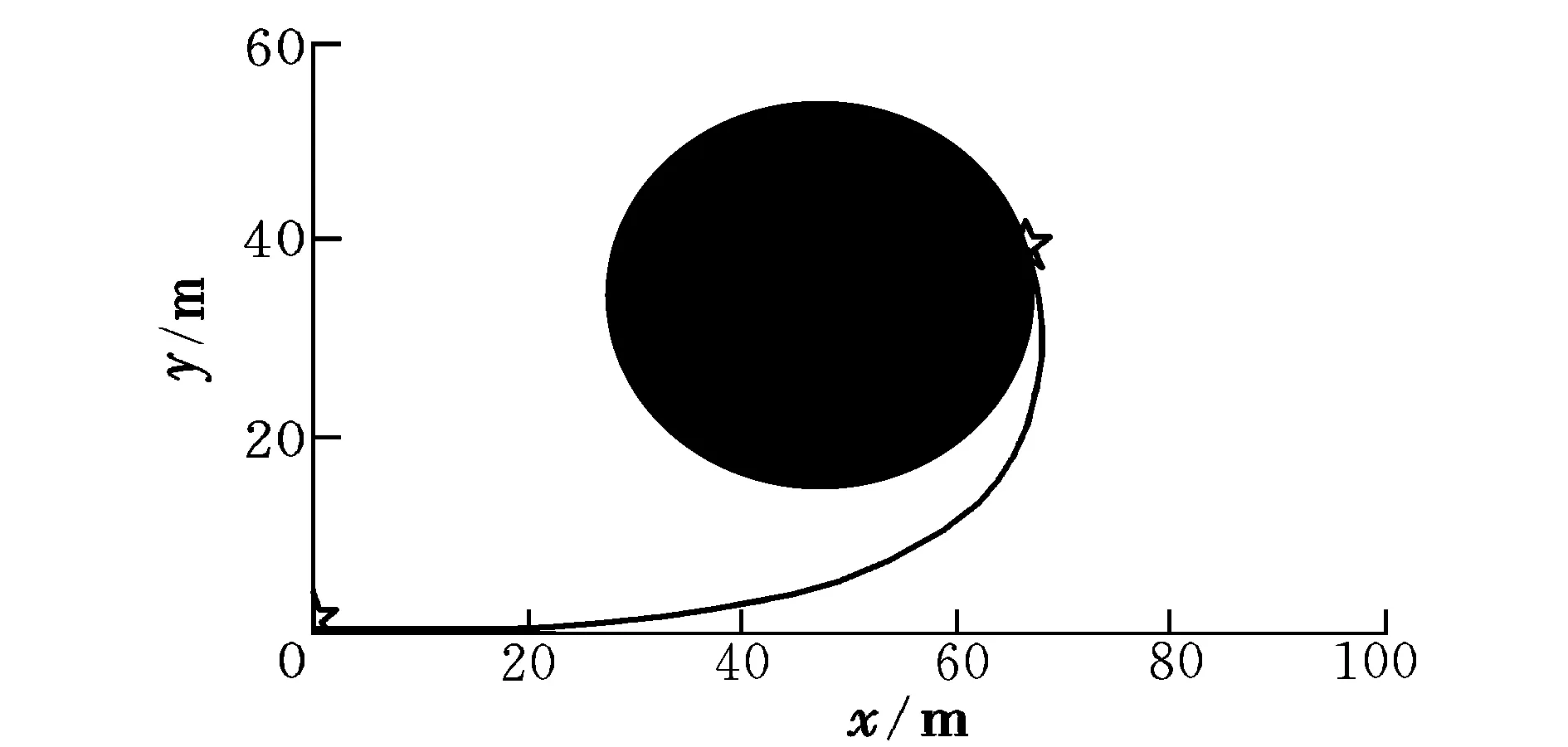
图3 顺时针PH螺线路径修正仿真Fig.3 Simulation diagram of path correction based on clockwise PH spiral
此时,PH螺线路径的最大曲率半径为κmax=0.043 m-1,而威胁障碍物的安全圆半径为R=20 m。因此,PH螺线路径满足相应的曲率约束条件,且不会侵犯威胁障碍物的安全圆。

图4 顺时针PH螺线路径曲率变化Fig.4 Curvature variation of clockwise PH spiral path
逆时针旋转位置关系如图5所示,图6则为PH螺线路径的曲率变化。
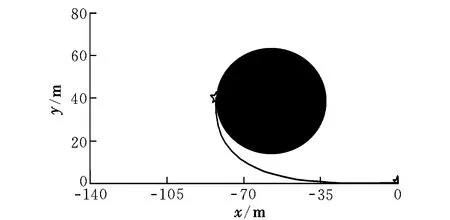
图5 逆时针PH螺线路径修正仿真Fig.5 Simulation diagram of path correction based on anticlockwise PH spiral

图6 逆时针PH螺线路径曲率变化Fig.6 Curvature variation of anticlockwise PH spiral path
此时,PH螺线路径的最大曲率半径为κmax=0.038 m-1,而威胁障碍物的安全圆半径为R=25 m。因此,PH螺线路径满足相应的曲率约束条件,且不会侵犯威胁障碍物的安全圆。
5 结束语
通过分析现有避障算法忽略可能存在的避障重规划路径侵犯威胁障碍物安全圆、降低了UAV避障重规划路径的安全性问题,在对障碍物安全圆侵犯问题详细分析基础上,考虑了避障路径重规划的性能约束及相应算法的复杂度和实时性要求,利用PH螺线路径连接直线与圆的方法解决了避障重规划路径侵犯威胁障碍物安全圆的问题。仿真结果验证了PH螺线路径对避障路径修正的有效性和可行性。本文提出的基于PH螺线的避障重规划路径修正方法实现简单,可提高UAV在复杂环境下执行任务的安全性。下一步将对三维空间避障重规划路径侵犯安全球的问题进行研究,并考虑UAV空间避障路径的曲率和挠率约束条件。
[1]White B A,Shin H S,Tsourdos A.UAV obstacle avoidance using differential geometry concepts[C]//Proceeding of the 18th International Federation of Automatic Control World Congress.2011:6325-6330.
[2]Han S C,Bang H,Yoo C S.Proportional navigation-based collision avoidance for UAVs[J].International Journal of Control,Automation and Systems,2009,7(4):553-565.
[3]包勇,符小卫,高晓光.势场理论的多无人机协同路径规划方法[J].火力与指挥控制,2012,37(3):10-12.
[4]张得舒,黄长强,丁达理,等.基于A*算法的无人机攻击轨迹解算[J].电光与控制,2011,18(3):18-20.
[5]张毅,杨秀霞,周硙硙.基于速度障碍法的多UAV可飞行航迹优化生成[J].系统工程与电子技术,2015,37(2):323-330.
[6]Mujumdar A,Padhi R.Reactive collision avoidance using nonlinear geometric and differential geometric guidance[J].Journal of Guidance,Control,and Dynamics,2011,34(1):303-311.
[7]吕盼稂,张珊珊,竺长安.基于Pythagorean速端螺线的平稳加工路径[J].中国机械工程,2006(23):2451-2453.
[8]Baass K G.The use of clothoid templates in highway design[J].Transportation Forum,1984(1):47-52.
[9]蔡华辉,王国瑾.三次C-Bézier螺线构造及其在道路设计中的应用[J].浙江大学学报(工学版),2010,44(1):68-74.
(编辑:崔立峰)
A re-planning path correction method for collision avoidance based on PH spiral
YANG Xiu-xia1, ZHOU Wei-wei2, ZHANG Yi1
(1.Department of Control Engineering, Naval Aeronautical and Astronautical University,Yantai 264001, China;2.The Bridge of Graduate Students, Naval Aeronautical and Astronautical University,Yantai 264001, China)
For the problem of existing obstacle avoidance algorithms, which ignores that the re-planning path violates threatening obstacle safety circle. A re-planning path correction method for collision avoidance based on Pythagorean Hodograph(PH) spiral was proposed. The related constraints of UAV path planning were considered in this method, and comparing to other correction algorithms, it had low complexity and high real-time performance, which can meet the requirements that UAV online avoided the dynamic and static obstacles. The simulation results show the practicality and efficiency of the re-planning path correction method for collision avoidance based on PH spiral.
obstacle avoidance; PH spiral; path planning; UAV
2016-01-08;
2016-04-19; 网络出版时间:2016-05-18 13:49
航空科学基金资助(20135584010)
杨秀霞(1975-),女,山东莱州人,副教授,博士,研究方向为飞行器智能控制及制导。
V249.1
A
1002-0853(2016)05-0086-05

