基于LMI的高超声速飞行器滑模预测控制

高海燕, 蔡远利, 唐伟强

(1.厦门理工学院 福建省高电压技术重点实验室, 福建 厦门 361024;2.西安交通大学 电子与信息工程学院, 陕西 西安 710049;3.兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050)



基于LMI的高超声速飞行器滑模预测控制

高海燕1, 蔡远利2, 唐伟强3

(1.厦门理工学院 福建省高电压技术重点实验室, 福建 厦门 361024;2.西安交通大学 电子与信息工程学院, 陕西 西安 710049;3.兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050)

针对高超声速飞行器非线性、多约束、快时变等特点,提出了一种基于线性矩阵不等式的滑模预测控制方法。首先设计系统的滑模面,然后对滑模面进行预测并将其作为优化性能指标,通过Schur补引理将控制律的设计转化为一个优化问题。该方法避免了常规滑模控制的高频切换,有效地克服了抖振现象。此外,相对于传统的滑模预测控制方法,该方法不需要额外计算终端约束条件和终端代价函数,只需要通过选取合适的李雅普诺夫函数即可保证系统的稳定性,且其加权矩阵和控制律是同时进行优化设计的,简化了设计过程。仿真试验表明,相比于单纯的预测控制和滑模控制,所提出的方法具有更好的跟踪性能。

线性矩阵不等式; 滑模预测控制; 渐近稳定; 高超声速飞行器

0　引言

高超声速飞行器是指飞行速度在5倍声速以上,在大气层或跨大气层实现高速远程飞行的飞行器[1]。与传统飞行器相比,由于采用机体/发动机一体化技术使其弹性机体、推进系统以及结构动态之间的耦合更强,系统的非线性更强,并且运行环境更加复杂,飞行过程中气热、气动特性变化更剧烈,迎角和舵偏等受到严格的约束条件限制。因此,对其进行控制器设计更具挑战性,其控制系统必须在保证输入和状态在给定约束范围的同时具有较强的鲁棒性[2]。

滑模控制作为一种特殊的非线性控制方法,其主要优势是对匹配的不确定性干扰能够精确补偿。滑模控制已经得到了理论界的重视[3-7]和工业界的青睐,如机械臂控制[8]、飞行器控制[9]、电机控制[10]等。然而,滑模控制系统中的高频振荡,即抖振现象,制约了该方法的进一步推广及应用。此外,滑模控制不具备约束处理能力,而且对不匹配干扰无法精确补偿,即会丧失完全鲁棒性[11]。

预测控制是一类新型的计算机控制方法,包含预测模型、滚动优化和反馈校正三大要素,其主要优势之一是能够有效地处理各种约束[12]。为了克服滑模控制的不足,发挥预测控制的优势,将预测控制的三大要素引入到滑模控制中,形成了一种新的控制方法,即滑模预测控制。滑模预测控制继承了滑模变结构控制的强鲁棒特性和预测控制的约束处理能力,近年来受到国内外学者的广泛关注[13-15]。在现有的滑模预测控制研究中,大部分只强调其消除抖振的能力,而忽略了预测控制的约束处理能力,即在控制律求解中忽略控制和状态的约束条件限制,得到解析形式的滑模预测控制律。此外,现有的滑模预测控制均需要设计终端代价函数和终端约束条件来保证系统的稳定性,但是终端代价函数和终端约束条件的计算是比较困难的,会大大增加预测控制律的优化计算时间。

为此,本文根据高超声速飞行器受到的约束条件限制,同时考虑现有滑模预测控制稳定性约束中的终端约束条件计算比较困难问题,提出一种基于线性矩阵不等式的滑模预测控制方法。

1　问题描述

本文以NASA Langley研究中心公开的高超声速飞行器纵向模型为研究对象[2],其典型的非线性运动方程为:

(1)

式中:V为速度;γ为弹道倾角;H为飞行高度;α为迎角;q为俯仰角速率。

本文采用文献[2]中给出的公开数据。在平衡巡航条件(V0=4 590.3 m/s,H0=33 528 m,γ0=0°,q0=0°)下,α0=1.79°时的力和力矩系数表达式如下:

(2)

其他参数,如转动惯量Iyy、质量m、地球半径RE等见文献[2]。

采用二阶系统来对发动机进行建模,即:

(3)

式中:ζ为二阶系统的阻尼;ωn为二阶系统的频率。

高超声速飞行器的控制目标是在受到控制和状态约束的条件下,通过调节升降舵偏转角δe和发动机节流阀指令βc,使得飞行器的速度和高度跟踪给定的参考信号。

2　滑模预测控制器设计

2.1滑模预测模型

忽略发动机动态过程,将高超声速飞行器的纵向非线性模型式(1)在平衡巡航条件下进行小扰动线性化,可得:

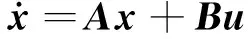
(4)

式中:x=[ΔV,Δγ,ΔH,Δα,Δq]T为状态向量,ΔV=V-V0,Δγ=γ-γ0,ΔH=H-H0,Δα=α-α0,Δq=q-q0;u=[Δβ,Δδe]T为控制向量。

假设高超声速飞行器受到的控制和状态约束条件为:

(5)

在滑模预测控制中,需要建立控制对象的预测模型。把速度和高度作为输出,将小扰动线性化模型式(4)离散化,得到:

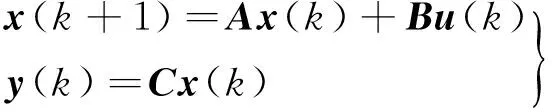
(6)

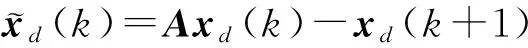
(7)

滑模面是与跟踪误差e(k)有关的,其设计可以参考文献[16]。根据文献[16]得到的滑模面为:

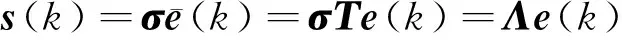
(8)

则滑模预测模型为:

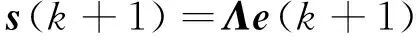
(9)

2.2反馈控制律设计

定义无穷时域性能指标:

(10)

式中:s为式(9)得到的滑模预测模型。

式(10)的性能指标可以写成两部分之和,即:

(11)

定义二次函数:

(12)

如果满足条件

V(e(k+i+1/k))-V(e(k+i/k))≤

(13)

则V(e(k+i/k))→0,i→∞。把式(13)从i=N加到i=∞,得到:

(14)

由滑模预测模型式(9)得到:

(15)

其中:

将式(15)代入式(11)的第2式,得到:

(16)

其中:

把式(14)代入式(11)的第3式,得到:

(17)

为了对控制律进行求解,可以采用矩阵的Schur补引理[17]将上面的约束条件化为线性矩阵不等式。

基于式(17),如果满足如下条件:

(18)

则J∞(k)≤γ1+γ2,因此,反馈控制律可以通过最小化性能指标上界γ1+γ2得到。

将式(16)代入式(18)第1式,有:

(G1e(k)+H1U)TW1(G1e(k)+H1U)+

(19)

采用Schur补引理,式(19)等价于:

(20)

将式(12)代入式(18),并由式(9)有:

(21)

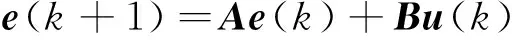
(22)

则:

(23)

将式(23)代入式(21),并令Q=P-1,得:

(24)

假定预测域N之后的控制律为状态反馈形式,即:

u(k+i|k)=F(k)e(k+i|k),i≥N

(25)

将式(9)和式(25)代入式(13),得到:

(26)

要使上式成立,只要:

(A+BF)TP(A+BF)-P+FTRF+

(27)

即可。

将Q=P-1代入式(27),得:

(28)

将上式左右同时乘以Q,并令Y=FQ,可得:

(AQ+BY)TQ-1(AQ+BY)-Q+YTRY+

(29)

采用Schur补引理将式(29)转化为如下线性矩阵不等式:

(30)

可以根据文献[18] 将控制与状态的约束条件式(5)转化为:

(31)

式中:a,b分别为状态和控制的维数;Ib×N为(b×N)×(b×N)的单位阵;Πm=[Im,…,Im]T;(xt,ut)为平衡点处的状态和控制;G,H是根据式(6)得到的,有:

综上,反馈控制律的计算转化为如下最小化问题:

若存在可行解,则得到控制量系列U,取第1个控制量作用于系统。

3　仿真结果及分析

以高超声速飞行器纵向非线性模型为仿真对象,在前文的平衡巡航条件下,假定从0时刻起分别给定飞行速度及飞行高度参考信号为Vr=30.48 m/s和Hr=30.48 m的阶跃信号。考虑迎角和控制的约束条件为:-4°≤α≤8°,0°≤β≤3°,-20°≤δe≤20°。在控制器设计中,选取滑模面加权矩阵Q=diag([1，1]),输入加权矩阵R=diag([1，1]),预测时域和控制时域均为N=10。采用文献[18]中的滑模控制方法和文献[19]的预测控制方法进行对比仿真,仿真结果如图1～图3所示。

从图1和图2可以看出:三种方法的速度和高度均能跟踪给定参考信号,滑模面均收敛到0的领域内;采用本文方法具有更快的收敛速度,高度具有更平稳的跟踪性能,这是因为本文方法结合了滑模控制和预测控制的优势,充分利用了控制能量。

从图3中可以看到,迎角和控制量均在给定约束范围内,本文方法的控制不存在抖振现象,这是因为提出的方法是通过优化求解得到控制律,而无需像滑模控制那样对控制律进行切换,从而消除了滑模控制的抖振现象。

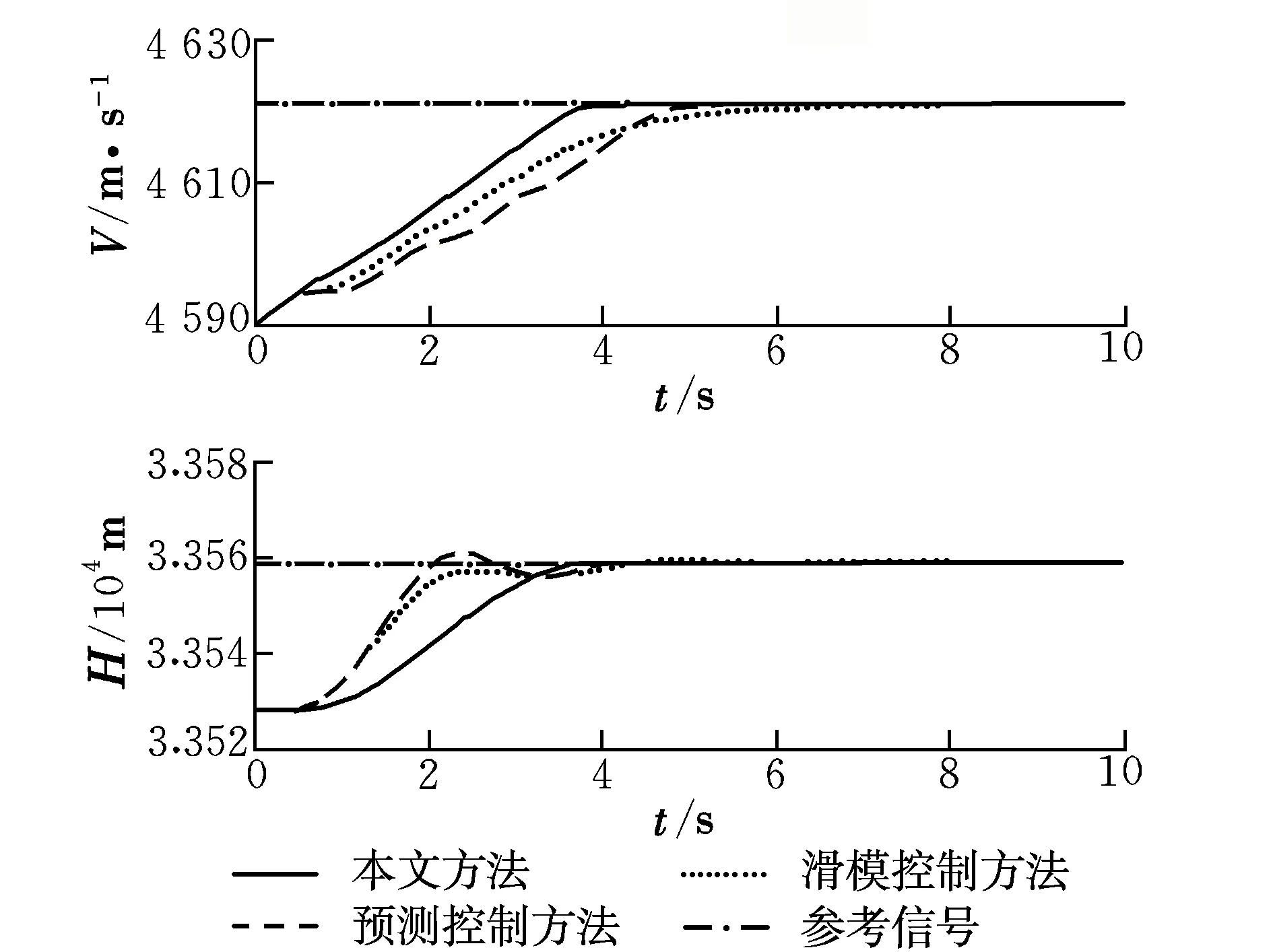
图1　输出跟踪指令信号Fig.1　Output tracking the command signals

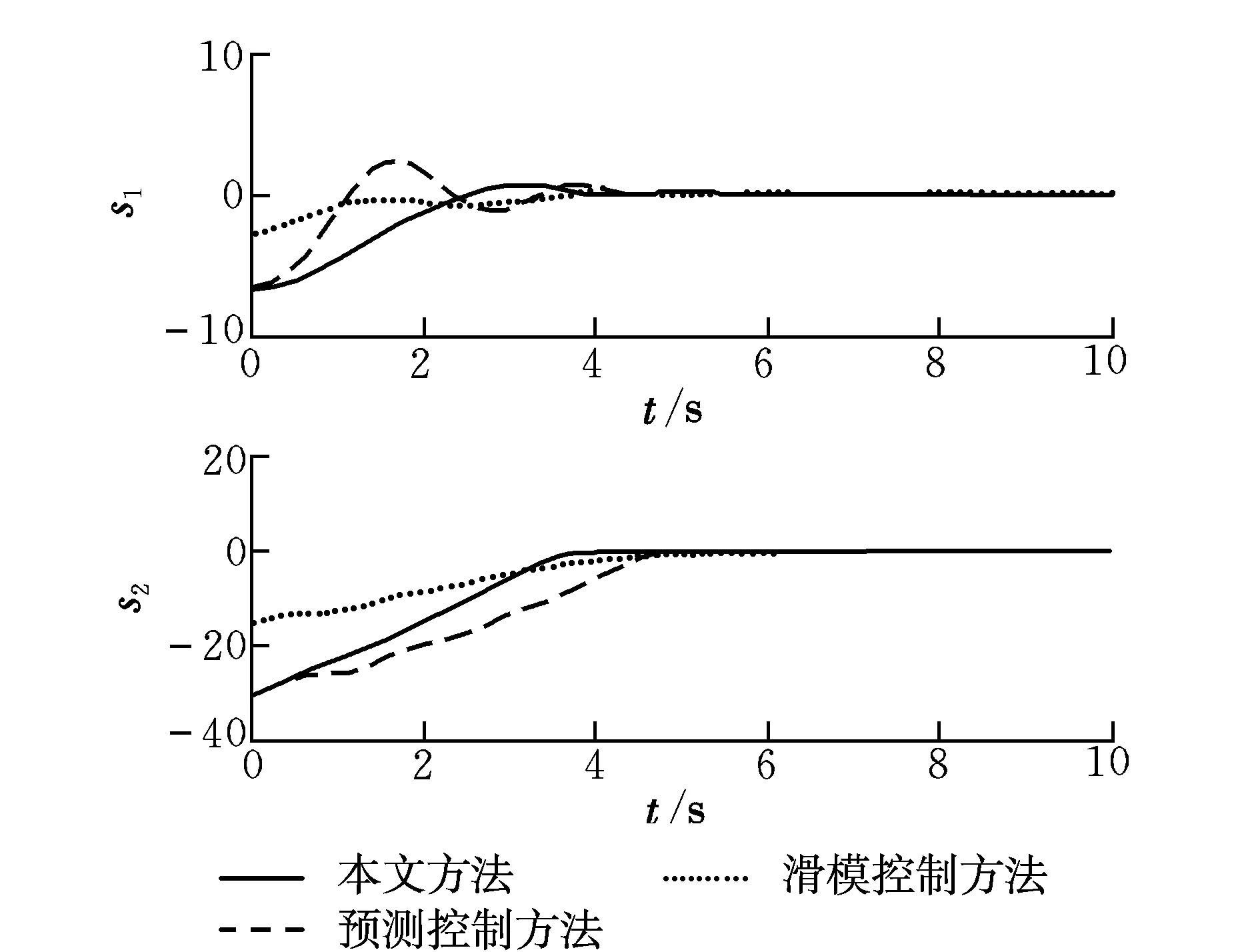
图2　滑模面响应曲线Fig.2　Sliding mode surface response curves

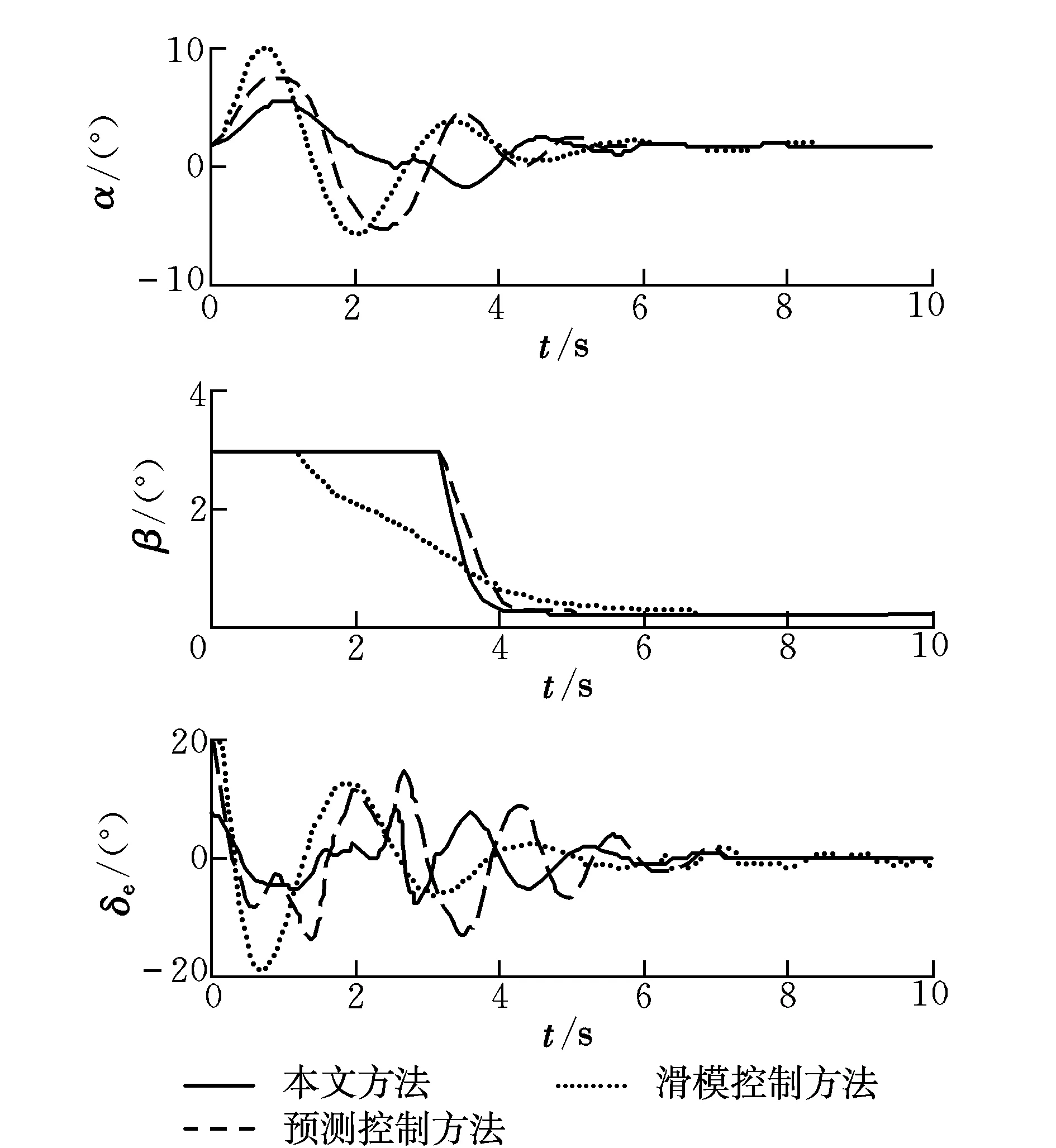
图3　迎角和控制量变化曲线Fig.3　Variation of angle of attack and the controls

4　结束语

针对高超声速飞行器受到的约束条件、滑模控制的抖振现象及其滑模预测控制的稳定约束条件较难求解问题,提出了基于线性矩阵不等式的滑模预测控制方法。该方法将控制律的设计转化为一个优化问题,避免了控制律的切换,从而消除了滑模控制的抖振现象。此外,控制律和李雅普诺夫函数的加权矩阵是同时进行优化设计的,简化了设计过程。最后,将本文提出的方法与滑模控制和预测控制进行对比仿真,验证了该方法的优越性。

[1]尉建利,王聪,葛颖琛,等. 高超声速飞行器操纵性/控制律一体化设计方法[J]. 固体火箭技术,2015,38(5):601-607.

[2]Xu H J,Mirmirani M D,Ioannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle [J].Journal of Guidance,Control,and Dynamics,2004,27(5):829-838.

[3]米阳,李文林,井元伟.基于幂次趋近律的一类离散时间系统的变结构控制[J].控制与决策,2008,23(6):643-646.

[4]高存臣,刘振,任启峰.时滞离散时间系统的非线性准滑模鲁棒控制[J].控制理论与应用,2013,30(1):123-130.

[5]刘金锟,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007,24(3):407-418.

[6]穆朝絮,余星火,孙长银.非奇异终端滑模控制系统相轨迹和暂态分析[J].自动化学报,2013,39(6):902-908.

[7]Feng Y,Yu X,Han F.On nonsingular terminal sliding-mode control of nonlinear systems [J].Automatica,2013,49(6):1715-1722.

[8]林壮,朱齐单,邢卓异.基于遗传优化的水平欠驱动机械臂分层滑模控制[J].控制与决策,2008,23(1):99-102.

[9]王亮,刘向东,盛永智.基于高阶滑模观测器的自适应时变滑模再入姿态控制[J].控制与决策,2014,29(2):281-286.

[10]Orlowska-Kowalska T,Tarchala G,Dybkowski M.Sliding-mode direct torque control and sliding-mode observer with a magnetizing reactance estimator for the field-weakening of the induction motor drive[J].Mathematics and Computers in Simulation,2014,98(2):31-45.

[11]Dong L,Tang W C.Adaptive back-stepping sliding mode control of flexible ball screw drives with time-varying parametric uncertainties and disturbances[J].ISA Transactions,2014,53(1):110-116.

[12]席裕庚.预测控制[M].长沙:国防科技大学出版社,1991:5-9.

[13]Xiao L F,Su H Y,Chu J.Sliding mode prediction tracking control design for uncertain systems [J].Asian Journal of Control,2007,9(3):317-325.

[14]Xiao L F,Su H Y.Multi-step prediction based discrete-time sliding mode control algorithm[C]//Second International Symposium on Intelligent Information Technology Application.NJ,USA:IEEE,2008:731-735.

[15]Rubagotti M, Raimondo D M,Ferrara A,et al.Robust model predictive control with integral sliding mode in continuous-time sampled-data nonlinear systems[J]. IEEE Transactions on Automatic Control,2011,56(3):556-570.

[16]高海燕,蔡远利. 高超声速飞行器的滑模预测控制方法[J].西安交通大学学报,2014,48(1):67-72.

[17]Boyd S,Ghaoui L E,Feron E,et al.Linear matrix inequalities in systems and control theory [M].Philadelphia:Society for Industrial and Applied Mathematics,1994:7-8.

[18]Ding B C,Xi Y G,Li S Y.A synthesis approach of on-line constrained robust model predictive control [J].Automatica,2004,40(1):163-167.

[19]刘金锟.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005:81-82.

(编辑：崔立峰)

Sliding mode predictive control for the hypersonic vehicle based on LMI

GAO Hai-yan1, CAI Yuan-li2, TANG Wei-qiang3

(1.High-voltage Key Laboratory of Fujian Province, Xiamen University of Technology,Xiamen 361024, China;2.School of Electronic and Information Engineering, Xi’an Jiaotong University,Xi’an 710049, China;3.School of Electrical and Information Engineering, Lanzhou University of Technology,Lanzhou 730050, China)

Considering the nonlinearity,multiple constraints and fast time-varying of hypersonic vehicle,we proposed a sliding mode predictive control strategy based on the linear matrix inequalities (LMIs). The sliding mode surface was designed first,and then it was predicted and regarded as the performance index. By using the Schur complement lemma,the design of the control law was converted to an optimization problem. Therefore, the frequent switching on the sliding surface was avoided and the chattering was suppressed. In addition,compared with the traditional sliding mode predictive control,the method does not need to calculate terminal constraints and terminal cost function additionally,and it only needs to choose suitable Lyapunov function to guarantee the stability of the system. And the weighted matrix and the control law are optimized simultaneously,which simplifies the design process. Simulations show that compared with the pure model predictive control and the sliding mode control,the proposed method has better tracking performance.

linear matrix inequalities (LMIs); sliding mode predictive control; asymptotic stability; hypersonic vehicle

2015-12-25;

2016-04-18; 网络出版时间:2016-05-18 13:49

国家自然科学基金资助(61308120，61463029)；厦门理工学院高层次人才项目资助(YKJ15022R)

高海燕(1986-)，女，福建龙岩人，讲师，博士，研究方向为飞行器制导与控制、预测控制。

TJ765.2

A

1002-0853(2016)05-0049-05