基于模糊理论的跳跃轨迹多目标优化设计

张勃, 唐硕, 泮斌峰

(1.西北工业大学 航天学院, 陕西 西安 710072;2.航天飞行动力学技术国家重点实验室, 陕西 西安 710072)



基于模糊理论的跳跃轨迹多目标优化设计

张勃1,2, 唐硕1,2, 泮斌峰1,2

(1.西北工业大学 航天学院, 陕西 西安 710072;2.航天飞行动力学技术国家重点实验室, 陕西 西安 710072)

针对探月返回跳跃轨迹的多目标优化设计问题,提出了一种基于模糊理论的优化设计方法,并对非线性隶属度函数对优化结果的影响进行了研究。首先,将连续的无限维优化问题进行离散化,转化为非线性规划问题;其次,用隶属度函数将各个子目标进行模糊化,将多目标优化问题转化为求模糊判决隶属度函数的最大值问题;最后,求解经过模糊化的非线性规划问题。分析了探月返回跳跃轨迹的特性,表明模糊多目标优化更能体现决策者的偏好。构造了具有不同凹凸性、不同形状的非线性隶属度函数,比较了它们对优化结果的影响,结果表明隶属度函数影响多目标模糊优化结果的首要因素是隶属度函数的凹凸性。

模糊理论; 探月返回跳跃轨迹; 多目标优化; 非线性隶属度函数

0　引言

探月是人类进行的最为复杂的航天探索活动之一。面对越来越复杂的航天任务,人们总是希望能够得到最优的结果,然而,实际中希望最优的目标往往不止一个。对于探月返回舱,其再入速度大,飞行时间长,加热量远大于近地轨道返回的飞船。另一方面,由于飞船为钝头体构型,没有气动舵面,为了减少姿态控制所需能量,通常要求飞船以最小的总控制量变化满足控制需求。由于多个目标之间存在的相互冲突和不可公度性使得最优解并不存在[1]。传统处理多目标优化问题的方法多是采用加权求和将多目标优化问题转化为单目标优化问题,然而多目标的不可公度性使得加权系数的选择具有盲目性,无法反映决策者的偏好。

模糊理论是解决多目标优化问题的有力工具之一。胡超芳[1]基于决策者满意度的思想,利用模糊优化方法对具有不同类型偏好信息的多目标优化问题进行了研究。张旭[2]对多种类型不明确决策偏好信息下多目标优化设计问题的建模和求解方法进行了研究和探讨。Wang等[3]以模糊多目标优化的方法研究了航空器的航迹规划,得到了较传统方法更为有效的结果。Li等[4]应用模糊多目标优化理论进行了环境友好的铁路规划研究。Ghannadpour等[5]研究了具有模糊时间窗口的动态车辆路线多目标优化问题。

探月返回轨迹优化设计的研究不乏其数,但都针对单一目标进行优化设计,不能很好地反映实际决策需求。本文以模糊理论为基础,对探月返回轨迹进行多目标、多约束的优化设计,比较分析基于模糊理论的多目标优化设计相对于传统加权求和方法的优越性。构造不同的隶属度函数,分析隶属度函数的选择对优化结果的影响,总结影响优化结果的隶属度函数特征量。

1　问题描述

1.1动力学方程

假设地球为均匀圆球体,考虑地球自转,则再入动力学方程为:

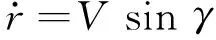
(1)

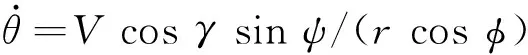
(2)

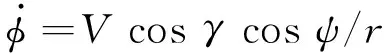
(3)

Ω2rcosφ(sinγcosφ-cosγsinφcosψ)

(4)

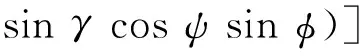
(5)

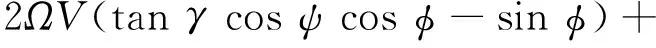
(6)

(7)

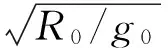
飞行过程中,飞行器通过调整迎角使得飞行处于配平状态,避免沿飞行器轴向出现翻转,可以认为迎角为马赫数的已知函数。为了控制飞行器的飞行轨迹,必须通过滚转使升力产生侧向分量,因此控制飞行轨迹的关键在于如何控制倾侧角σ。

1.2过程约束及终端约束

对于探月返回再入飞行器,再入速度比近地轨道再入速度更大,气动加热更为严重,因此必须保证热流不大于允许值。对于钝头体一般没有气动控制面,因此不存在动压约束。过载是钝头体再入时需要考虑的重要约束,它与飞行器的结构安全、设备完好以及乘员的生命健康息息相关。因此本文仅考虑过载和热流约束:

(8)

对于小升阻比飞行器,轨迹的终端约束为开伞点的高度、速度以及开伞点的位置,其中开伞点的高度与速度可以合并为开伞点的能量[6],所以终端约束为:

(9)

1.3上下边界约束

在飞行过程中飞船以配平迎角飞行,所以控制量为倾侧角。由于引入了虚拟控制量uσ,通过直接控制uσ的变化来达到控制倾侧角σ的目的,因此可以认为σ为状态量,uσ为控制量,则对倾侧角及虚拟控制量的约束为:

(10)

1.4性能指标

由于飞船为钝头体构型,没有气动舵面,为了减少姿态控制所需能量,通常要求飞船以最小的总控制量变化满足控制需求,即:

(11)

如前所述,再入过程中的吸热量应尽可能小,因此其中另一个性能指标为:

(12)

1.5多目标优化问题

为了便于多目标优化问题的描述,令状态向量x(t)=[r,θ,φ,V,γ,ψ,uσ]T,控制量u(t)=uσ,则动力学方程可记为:

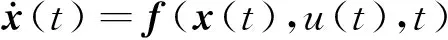
(13)

路径约束式(8)记为:

(14)

终端约束式(9)记为:

(15)

上下边界约束式(10)记为:

(16)

(17)

目标向量定义为:

(18)

则多目标优化问题可以描述为:寻求控制变量u(t),使得目标向量J达到最小,即分别使J1,J2,…,Jn达到最小,同时满足约束式(13)～式(17)。

通常情况下,使J1,J2,…,Jn都达到最优的绝对最优解是不存在的,只能求得Pareto最优解。如何从众多的Pareto解中根据决策者的需求找出唯一的一个解是多目标优化的关键。根据决策者的偏好,不同的目标给予不同的权重,即:

(19)

把多目标优化问题转化为单目标优化问题。但是由于多目标的不可公度性,使得权系数难以选择,导致权系数不能反映决策者的偏好。而通过模糊理论,用隶属度函数来反映决策者对目标的满意程度,把目标函数的加权求和转化为关于隶属度函数的单目标优化问题,可以很好地解决直接加权求和方法的不足:

(20)

式中:μ1(x),…,μn(x)为模糊集的隶属度函数。

2　模糊理论与目标模糊化

首先用隶属度函数描述决策者对目标的满意度,隶属度函数的值越大,满意度越高,反之亦然;然后根据对不同目标的满意度要求不同而赋予不同的权值。最为常用的隶属度函数为线性隶属度函数,对于极小化问题,线性隶属度函数可以表示为[7]:

(21)

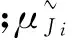
第i个模糊目标集可表示为:

(22)

将目标函数模糊化后,就可以构造模糊判决。模糊判决的模型有对称模型、加权模型、几何平均模型和非对称模型[8]。由于加权模型可以根据决策者的需要,突出重要目标,更具灵活性,因此本文采用加权模型来构造模糊判决。即:

(23)

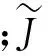
(24)

(25)

3　隶属度函数

对于最大化和最小化问题,当隶属度函数的值在区间(0,1)变化时通常是严格单调递增或严格单调递减的,即要么目标值越大满意度越高,要么目标值越小满意度越高。因此有:

(26)

对于同一多目标优化问题,隶属度函数的单调性是确定的。但是当选取不同的隶属度函数时,它们的凹凸性是不同的。为了研究隶属度函数的选取对优化结果的影响,本文构造了具有不同凹凸性质的隶属度函数,分别进行计算对比。令:

(27)

为了表述方便,本文只列出隶属函数在区间(Jimin,Jimax]的表达式。

幂函数:

(28)

指数函数:

(29)

对数函数:

(30)

反三角函数:

(31)

多项式:

(32)

(33)

4　仿真分析

4.1飞行器模型与再入条件

本文采用的飞行器质量为8 382 kg,再入时以配平迎角飞行。飞行过程中最大倾侧角速率为20 (°)/s,过载的最大值不超过10,最大热流不超过150 W/cm2[9]。初始状态和终端约束如表1所示。

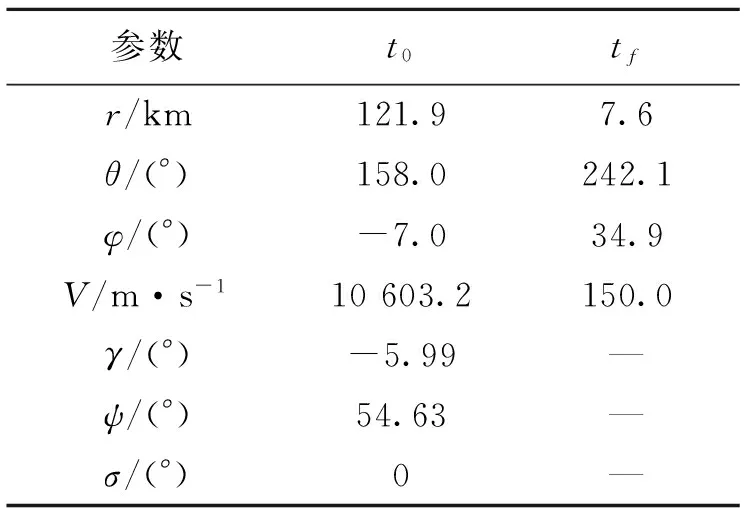
表1　初始状态和终端约束

4.2模糊多目标轨迹优化

为了与传统直接加权求和方法作对比,针对优化目标式(11)和式(12),定义加权目标函数如下:

(34)

式中:ω=0.1, 0.5, 0.9(当ω=0.1时，表明目标最小吸热量比最小总控制量变化更重要;ω=0.9时正好相反;ω=0.5时，表明二者的重要性相同)。模糊优化的目标为模糊判决的隶属度函数式(24),即:

(35)

权重系数的选择与直接加权求和的权系数相同,便于对结果进行比较。隶属度函数采用简单的线性隶属度函数。

图1为直接加权求和方法与模糊优化方法优化结果的高度剖面的对比。可以看出:直接加权求和方法并不能准确反映决策者的偏好,当ω变化时,高度剖面几乎没有变化或变化很小;而模糊优化方法的结果随着决策者的偏好不同而出现了明显的改变,反映了决策者的偏好对优化结果的影响。

图2给出了两种不同方法下优化结果倾侧角的变化规律。可以看出:直接加权求和方法得到的倾侧角变化并没有呈现一定的渐变性,并且倾侧角的剧烈变化并没有引起其他量的相应变化;ω越大,倾侧角的变化越趋于平缓,越有利于减小总控制量的变化,体现了较大的ω对总控制量变化最小的偏好。

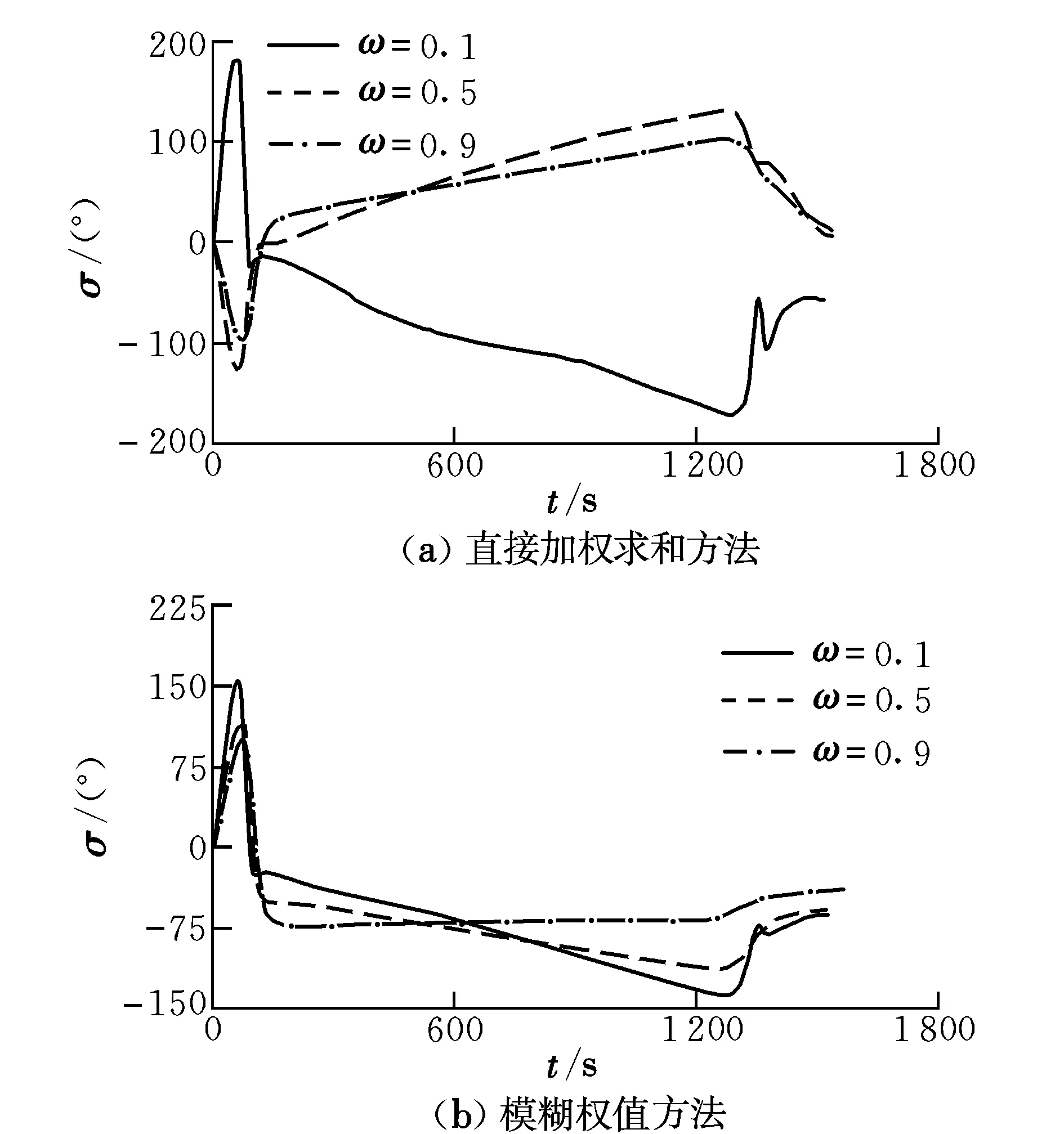
图2　不同权重下优化结果倾侧角剖面对比Fig.2　Comparison between the bank-angle profiles of optimized results at different weights

图3给出了两种方法下目标函数和子目标函数随权重系数变化的影响结果。可以看出,直接加权求和方法中的权系数对子目标的影响非常小,权系数几乎不能起到调节子目标的作用。当较大子目标占的比例越来越小(重要性越来越低)时,加权求和目标函数几乎呈线性减小,而子目标却基本保持不变。相反地,模糊优化方法中模糊判决的隶属度函数仅在小范围平缓变化,而子目标的隶属度函数随着其对应权值的变化而发生明显的改变。权值增大则子目标对应的隶属度函数增大,权值减小则子目标对应的隶属度函数减小,权值(或决策者偏好)对子目标的调节作用再一次得到了验证。

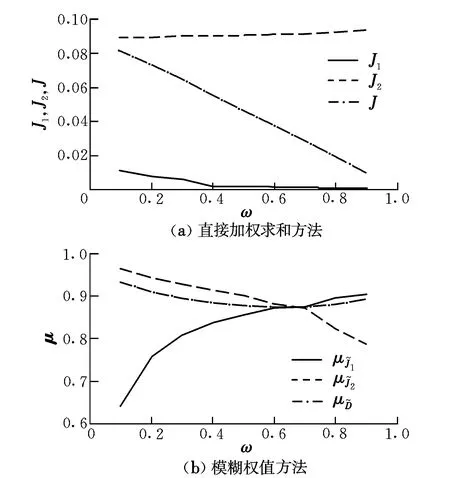
图3　两种方法权重对最优目标的影响结果Fig.3　Effect of the weight methods on the optimum objective

4.3隶属度函数对优化结果的影响

按照非线性隶属度函数的二阶导数符号的不同,可以将隶属度函数分为凸隶属度函数(p<0)和凹隶属度函数(p>0)。同一组的隶属度函数具有相同的形状,并且关于直线μ=z对称,具有不同的凹凸性。

图4给出了采用不同组别(即不同形状)的隶属度函数所求得的优化结果。可以看出:对于具有不同形状但凹凸性相同的隶属度函数,其优化结果相差不大;但是,对于即使形状完全相同而凹凸性不相同的隶属度函数,其优化结果具有很大不同。因此,隶属度函数的凹凸性是影响优化结果的一个重要因素,而隶属度函数的形状对优化结果的影响不大。

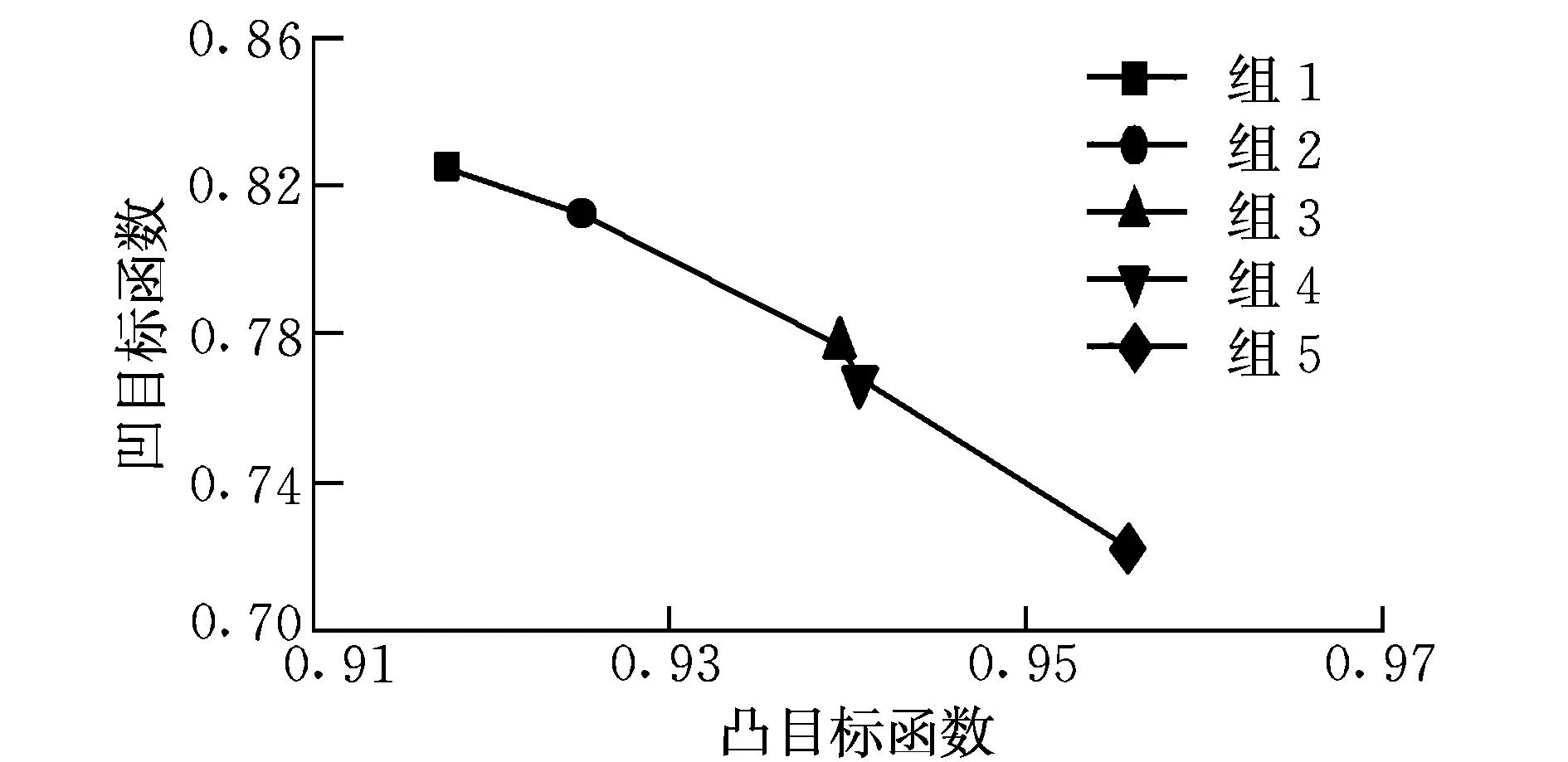
图4　不同组别隶属度函数优化结果分布Fig.4　Distribution of the results of different groups

图5为不同组别隶属度函数的优化结果。可以看出,不同形状的优化结果几乎处于同一直线上,即不同形状隶属度函数的优化结果是近似线性相关的,进一步证明了隶属度函数的形状对优化结果的影响是很小的。

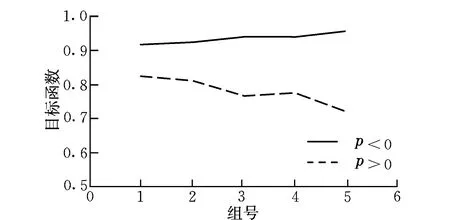
图5　不同组别隶属度函数优化结果Fig.5　Optimization results of the member function in different groups

5　结束语

本文研究了探月返回跳跃轨迹的多目标模糊优化设计问题,应用模糊理论将多目标优化问题转化为单目标优化问题,并分析了不同非线性隶属度函数对优化结果的影响。研究结果表明,多目标模糊优化更能体现决策者的偏好,适合于探月返回轨迹的多目标优化设计,并且影响模糊优化结果的首要因素是隶属度函数的凹凸性,而隶属度函数的形状对优化结果的影响不大。研究结果对探月返回轨迹的优化设计具有一定的参考价值和指导意义。

[1]胡超芳.基于决策者满意度的多目标模糊优化算法研究[D].上海:上海交通大学,2007.

[2]张旭.决策信息不明确的多目标模糊优化模型与方法[D].大连:大连理工大学,2009.

[3]Wang Y Y,Wei T T,Qu X J.Study of multi-objective fuzzy optimization for path planning[J].Chinese Journal of Aeronautics,2012,25(1): 51-56.

[4]Li X,Wang D C,Li K P,et al.A green train scheduling model and fuzzy multi-objective optimization algorithm[J].Applied Mathematical Modelling,2013,37(4):2063-2073.

[5]Ghannadpour S F,Noori S,Tavakkoli-Moghaddam R,et al.A multi-objective dynamic vehicle routing problem with fuzzy time windows:model,solution and application[J].Applied Soft Computing,2014(14):504-527.

[6]Xue S,Lu P.Constrained predictor:corrector entry guidance[J].Journal of Guidance,Control,and Dynamics,2010,33(4):1273-1281.

[7]胡宝清.模糊理论基础[M].武汉:武汉大学出版社,2010:1-7.

[8]邓斌,黄洪钟,王金诺.多目标模糊优化的数学模型及其求解原理和方法[J].机械设计与研究,1996(1):8-13.

[9]Brunner C W.Skip entry trajectory planning and guidance[D].Iowa:Iowa State University,2008.

(编辑：崔立峰)

Fuzzy theory based multi-objective optimization of lunar return skip trajectories

ZHANG Bo1,2, TANG Shuo1,2, PAN Bin-feng1,2

(1.School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China;2.National Key Laboratory of Aerospace Flight Dynamics, Xi’an 710072, China)

A fuzzy theory based multi-objective optimization method was proposed for the lunar return skip trajectory design and analysis,and the effect of nonlinear member functions of fuzzy sets on the optimization results was investigated. The optimization problem was converted to a nonlinear programming problem. Then each sub-objective was fuzzed to obtain the fuzzy decision set and its member function. Thus,the original multi-objective optimization problem was converted to a single-objective optimization problem which maximizes weighted sums of the member functions. The optimization results demonstrate that the proposed method can well show the preference of the decision maker. Nonlinear member functions with various shape and different concavity and convexity were constructed to investigate the main factor that affected the optimization results,and the results show that the concavity and convexity of member functions have much larger effect on the optimization than that of the shape.

fuzzy theory; lunar return skip trajectories; multi-objective optimization; nonlinear member function

2015-12-17;

2016-04-18; 网络出版时间:2016-05-18 13:49

张勃(1988-)，男，陕西商洛人，博士研究生，研究方向为飞行器轨迹规划与制导。

V412.4

A

1002-0853(2016)05-0059-05