企业经营决策方案评价的敏感度分析
羊 英
(上海第二工业大学经济管理学院,上海 201209)
对企业经营决策方案的综合评价是为了确定决策方案的可行性和决策的优化程度。评价方式一般有两种:方案排序或取最优(大多数时候是满意解)。企业经营中遇到任何的变动都会影响到方案排序结果或者满意解,因此研究决策方案评价结果的稳定性和敏感度非常必要。
企业经营决策方案评价属于多目标决策分析问题,在对多目标决策问题敏感度分析的研究中,主要侧重于研究权重变化的敏感度。如UZAY等提出了对模糊多属性决策问题的权重敏感度分析[1],CHEN等对 AHP模型的敏感度进行了分析[2],樊治平[3]、陈守煜、刘金禄等对模糊优选模型的权敏感度进行了分析[4-5];另外一类是对决策结论或决策函数稳定性的分析,如蒋艳等研究了方案排序对权重的敏感度[6-9],刘慧等研究了决策结论的敏感度[10]。在以上研究中尚未发现对经营决策方案选择或排序的敏感度进行分析的例子。ANP模型能够反映企业经营决策方案中决策变量的层次关系和关联关系,但要研究环境变化对经营决策方案选择的影响,就必须研究ANP模型的敏感度[11-15]。虽然已有的Super Decision软件能够对ANP模型进行计算和初步的敏感度分析,但针对经营决策中比较复杂的环境,这些分析还不够,因此笔者对企业经营决策方案评价建立ANP模型,基于该模型,在文献[2]的基础上改进算法,着重研究ANP模型中权重以及因素关联性的敏感度分析算法,并将其运用到企业经营决策方案评价中,着重分析决策方案对子目标制定以及环境变化的敏感度。
1 企业经营决策方案评价模型
从长远发展来看,企业经营决策的总目标是提高企业竞争力,这个总目标又可以细分为4个子目标:企业价值增殖、提高客户满意度、快速反应和持续发展能力。每个子目标下有多个属性。在选择和评价选择方案时根据各个方案每个属性取值进行综合评判。综合已有的研究,可建立企业经营决策方案评价指标体系,如表1所示。另外,着重分析4个子目标之间的关系,发现子目标之间互相依赖、互相影响,其关系如图1所示。在图1中,箭头指向代表该子目标对另一子目标有影响。表1中每个指标后面的数字为使用模糊ANP评价方法获得的指标权重。

图1 竞争子目标之间的相互依赖关系
综合表1和图1发现,企业经营决策方案评价涉及到多个层次和多个属性,且在子目标层面上,子目标制定之间存在依赖性,因此当决策环境发生变化或者某个决策属性发生变化时,会对决策方案的选择带来什么样的影响,需要对该评价模型进行敏感度分析。

表1 企业经营决策方案评价指标体系及其初始权重
2 模型的敏感度分析算法
2.1 符号设定
为了研究方便,以下先对要使用的符号进行说明:GOAL为决策总目标;Si为第i个子目标(i=1,2,…,L);Cm为第 m 个属性(m=1,2,…,M);Ak为第 k个决策方案(k=1,2,…,K);L 为子目标个数;M为属性个数;K为决策方案个数;CAk为第k个决策方案对总目标的作用;r为i的顺序号,如果,Ar的顺序号在 Ar+n的前面;CSl为第l个子目标对总目标的作用;Sl为考虑子目标依赖的子目标之间两两比较的权重;为第m个属性对第l个子目标的作用;为第k个决策方案对第m个属性的作用;为第k个决策方案对第l个子目标的作用;为第i个子目标对第j个子目标的作用值,其中 i≠j,且 i,j=1,2,…,L(该指标用于分析子目标之间的依赖关系)。
在这里“作用”是指属性权重、绩效价值或贡献,这个参数在不同层次上含义不尽相同:不同子目标对企业总目标是绩效或价值;不同属性对子目标是影响权重;而决策方案对属性是贡献。总的来说,不管是何种类型都可以说是下一层因素对上一层的作用。各层作用值之和都为1,即:


在ANP模型里计算每层作用值时还需要考虑该层各元素之间的关联作用,关联作用和两两对比的结果综合后才可以得到每层各个元素的作用值,以该模型中子目标层为例,其计算过程如下:首先,对于第h个子目标,分别基于该子目标将其他子目标(l≠h)进行两两比较,得到矩阵C,其中,对于i=h,则可以取1,综合得到矩阵,将其与之前子目标两两比较得到的矩阵Sl(l=1,2,…,L)相乘,即得到每个子目标对目标的作用值:

另外,第k个决策方案对总目标的作用是每个决策方案对子目标的作用和子目标对目标作用的叠加效果,即:
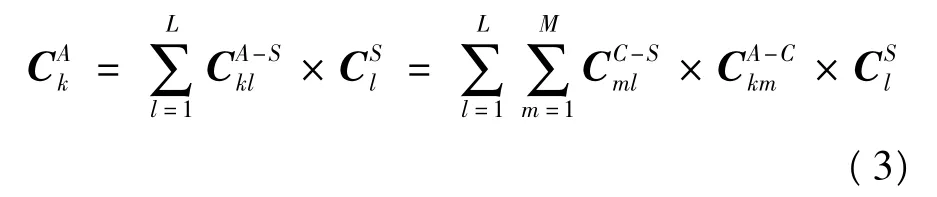
2.2 模型的敏感度分析算法描述
从式(2)可知,子目标对目标的作用值由两部分组成,因此,必须从两个方面来分析子目标之间依赖性敏感度。
2.2.1 子目标权重敏感度分析
子目标层上各子目标的权重为Sl,对其敏感度进行分析。现假设仅对子目标之间两两对比的权重进行扰动,其扰动值为PS。对l*个子目标的作用值Sl扰动为PSSl*,根据文献[2]的分析,PSSl*取值满足:

另外有:

若 λS>0,则有若 λS<0,则有再结合式(4),则可以判断的允许扰动取值范围和保持子目标作用值不变的扰动范围(称为容忍范围)。
可以定义两个敏感度系数:OPSC为当前作用值到容忍值边界的距离,它依赖于当前作用值和变化的方向(增加还是减少);TSC为容忍范围,范围越小,证明对应元素越敏感。
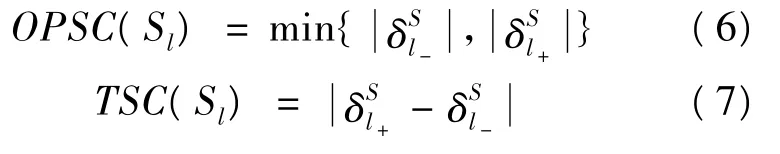
要分析各个子目标的敏感度,依次计算各个子目标(l*=1,2,…,m,m 个子目标)下 r=1,2,…,(m-1),n=1 的 PSSl*、OPSC(Sl)、TSC(Sl)值即可。
2.2.2 子目标之间依赖性的敏感度分析
在以上分析中,讨论到ANP模型中子目标之间存在关联关系,即基于某一子目标(也就是以这个子目标作为目标)对比其他子目标之间重要程度,可形成矩阵,以下简写为Cij。当以某一子目标为目标时,其他子目标对比重要度发生变化,就会引起Cij的变动,以下对Cij的敏感度进行分析。
现假设对Cmn的扰动为Qmn,且必须满足m≠n(因为在 Cij中,若 i=j则 Cij=1),且有:

对Cmn加以扰动,即以第n个子目标作为目标比较其他子目标的重要程度,由于Cnn=1,因此对Cmn的扰动不会影响到Cnn的值(也即第n个子目标对自己不会有什么改变),从而第n行的Cij都不会发生改变,因此有CSn的值(也即第n个子目标对目标的作用值)保持不变。另外对于CSn以外的其他CSi的值分两种情况加以考虑。
(1)首先考虑:

(2)接下来考虑CSi(i≠n)的值。
当i=m时,有:

当 i≠m,n 时,有:

3 算例分析
3.1 设定决策方案
案例分析基于制造行业的子目标决策层,假设现有3套决策方案,分别为:A(大规模生产模式,大投入);B(中等规模生产模式,中等投入);C(小规模生产模式,小投入)。
依据表1给出的指标体系和权重对3个决策方案进行评价,得到初始评价结果为(0.62,0.55,0.59)即 A>C >B,A为最优方案。
3.2 子目标权重敏感度分析
当企业根据市场形势或环境变化调整子目标时,子目标之间两两比较权重发生变化,从而影响子目标对目标的作用值。在怎样的变动范围内不会改变子目标对目标的作用值,以及权重变化会给作用值带来多大变化将直接影响决策方案的选择。假设已有计算结果如表2~表4所示。

表2 CSl的值

表3 Sl的值
表4 的值
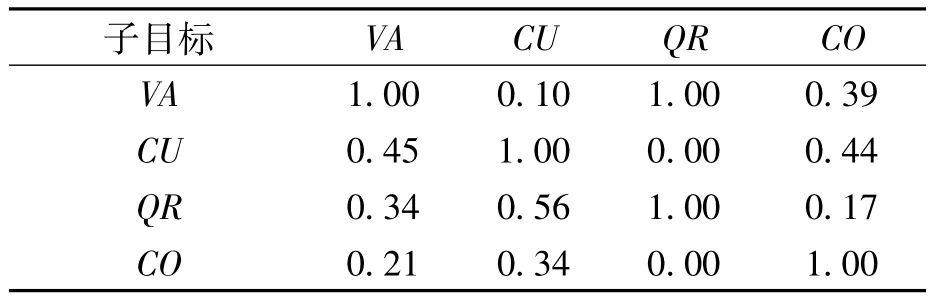
表4 的值
子目标39 CU 0.45 1.00 0.00 0.44 QR 0.34 0.56 1.00 0.17 CO 0.21 0.34 0.00 1.00 VA CU QR CO VA 1.00 0.10 1.00 0.
表2为4个子目标的初始权重,表4为考虑子目标两两之间依赖性的比较矩阵,表3为综合表2和表4后的结果。
改变Sl的值以观察其对决策方案选择的影响,以及其改变值的容忍范围。按照以上计算公式进行计算,结果如表5所示。

表5 子目标权重变动对子目标作用值敏感度分析
分析表5的结果发现,最小的TSC值出现在S1上,为0.038,表明第一个元素的权重最为敏感,也就是说如果改变第一个子目标的重要程度将很容易影响到子目标对目标的作用值排序。另外,这4个子目标权重的OPSC值都比较小,均小于或等于0.010,意味着目前权重离容忍值边界都非常近,也就是说任何一个权重变动超过0.010就会影响到其对目标的作用值排序。这进一步说明了考虑子目标之间关联关系,比只考虑各个子目标对目标的贡献,其作用值要敏感得多。因此,在企业确定子目标发展方向时,对子目标重要程度比较衡量非常重要,改变子目标中心就会影响到子目标对目标的作用值,从而对决策方案的选择产生影响。
3.3 基于某一子目标的其他子目标之间依赖性的敏感度分析
仍以表2~表4所示的数据为例进行分析,现在假设以企业价值增值为目标对其他3个子目标的重要程度进行重新比较,增加客户满意度子目标的权重,即调整C21的值,增加Q21,属于以上第二种情况。因此有另外有-0.45≤Q21≤0.55,所以 Q21的容忍范围为[-0.45,0.04]。其 OPSC 值为 0.04,TSC 值为0.49。也即在以企业价值增殖为目标的情况下,客户满意度的权重相对于其他两个子目标增加超过0.04则会使得4个子目标对企业总目标的作用值排序发生改变。
因此,企业在制定总的发展目标时,各个子目标的应用和相互之间的依赖关系如果发生变化会影响到子目标对总目标的作用,从而企业在子目标调整时必须相应调整决策方案。
4 结论
决策的关键在于选优,而最优方案的稳定性到底如何,则要分析其敏感度。笔者针对企业决策方案评价的ANP模型的子目标权重以及子目标之间的依赖性分析其敏感度,给出了不同子目标层权重的敏感度分析算法和子目标之间依赖性的敏感度分析算法,基于该算法,可以分析子目标权重变化以及子目标依赖性变化对最终决策的影响。笔者采用该方法分析了企业经营决策的ANP模型4个子目标对3种决策方案的敏感度,最终得出了结论。研究成果对企业决策分析和制定最优决策方案具有参考价值。
[1] UZAY K,HANS R,VAN N L.A sensitivity analysis approach to introducing weight factors into decision functions in fuzzy multicriteria decision making[J].Fuzzy Sets and Systems,1998(97):169-182.
[2] CHEN H Y,DUNDAR F K.A sensitivity analysis algorithm for hierarchical decision models[J].European Journal of Operational Research,2008(185):266-288.
[3] 樊治平,尤天慧,张全.多属性决策中基于加权模型的属性值灵敏度分析[J].东北大学学报:自然科学版,2002,23(1):83-86.
[4] 陈守煜,刘金禄,伏广涛.模糊优选决策模型的权敏感全局估计与应用[C]//2001中国控制与决策学术年会论文集.[S.l.]:[s.n.],2001:906-910.
[5] 刘金禄,陈守煜.模糊优选模型的权灵敏度分析及其应用[J].水电能源科学,2002,20(4):54-56.
[6] 蒋艳,岳超源.方案排序对权重比例变化的敏感性分析[J].华中科技大学学报:自然科学版,2002,30(8):24-26.
[7] 熊文涛,刘三阳,李卫华.一种基于灵敏度分析的多属性权值确定方法[J].武汉理工大学学报,2004,26(12):92-95.
[8] 刘华祥,施其洲.多目标决策中权重灵敏度分析的计算机模拟[J].交通与计算机,2006,24(2):105-107.
[9] 蒋艳,岳超源.方案排序对属性值的敏感性分析[J].武汉理工大学学报:信息与管理工程版,2003,25(5):86-89.
[10] 刘慧,韩兵,戴锋.决策结论的敏感度分析[J].中国管理科学,2008,16(专辑):104-107.
[11] JEFFREY L R.Lp-metric sensitivity analysis for single and multi-attribute decision analysis[J].European Journal of Operational Research,1997(98):563-570.
[12] DAVID B A.Sensitivity of multi-criteria decision making to linguistic quantifiers and aggregation means[J].Computers & Industrial Engineering,2005(48):289-309.
[13] 王四春,张泰山,殷志云,等.基于 GP的多目标决策函数稳定性分析[J].计算机研究与发展,2005,42(8):1318-1323.
[14] 范培蕾,张晓今,杨涛.基于灵敏度分析的 Pareto解改进计算方法[J].系统工程与电子技术,2009,31(12):2977-2981.
[15] 张朝昆,王会英.模糊多目标决策灵敏度分析及应用[J].重庆工学院学报:自然科学版,2009,23(8):126-134.

