近地航天器量子导航定位卡尔曼滤波算法研究
王志刚, 邓逸凡, 杨绚
(1.西北工业大学 航天学院, 陕西 西安 710072;2.航天飞行动力学技术国家重点实验室, 陕西 西安 710072)
近地航天器量子导航定位卡尔曼滤波算法研究
王志刚1,2, 邓逸凡1,2, 杨绚1,2
(1.西北工业大学 航天学院, 陕西 西安 710072;2.航天飞行动力学技术国家重点实验室, 陕西 西安 710072)
针对近地航天器量子导航定位系统,为了进一步提高其定位精度,利用滤波技术将QPS测量值结合航天器的运动模型进行状态量的滤波估计。给出了基于基线干涉原理的量子定位系统观测方程和以二体运动为主的航天器轨道运动模型,在此基础上详细推导了扩展卡尔曼滤波处理过程,并针对该模型进行了仿真。仿真结果表明,基于EKF的量子导航定位精度有明显提高。
量子导航; 卡尔曼滤波; 定位精度
0 引言
量子定位系统(Quantum Positioning System,QPS)是采用具有量子特性的脉冲信号,基于基线干涉原理实现定位的。它可以突破经典无线电导航体制的定位精度上限,并具有较高的安全性[1-2]。2005年,美国陆军研究实验室的Bahder博士基于传统卫星定位系统的设计思想提出了星基量子定位系统的总体设计方案[1]。Bahder进行的仿真计算表明,忽略重力场以及大气的影响,同时假定坐标系统是封闭的,不受其他因素影响,采用量子定位系统进行定位,误差(标准偏差)可低于1 cm。在国内,文献[3-6]研究了QPS的研究现状、潜在优势和发展趋势等。研究表明,QPS的一个显著特点就是具有极高的定位精度和很高的安全性,能够检测入侵者的存在。可见,量子定位技术具有非常大的研究价值和应用潜力。对于传统组合导航系统,为了提高其精度,通常是利用卡尔曼滤波算法将不同导航器件的量测信息和系统状态信息融合。王恒等[7]基于卡尔曼滤波器的基本原理,详细推导了适用于自旋卫星章动控制的卡尔曼滤波处理过程。刘爱元等[8]在分别设计了惯性导航系统模拟器以及卫星导航模拟器的基础上,针对如何实现两个系统的最优组合,设计了组合导航卡尔曼滤波器。
为进一步提高量子导航定位精度的影响,本文利用滤波技术将QPS测量值结合航天器的运动模型进行状态量的滤波估计,以期获得高于单独QPS定位的导航精度。
1 观测方程
量子导航模型的推导是基于基线干涉原理[1]进行的,其示意图如图1所示。基线干涉方法测量的是不同光路的脉冲时延之差,即到达时间差,到达时间差反映了两条路径的距离差。假设E1位于基线中点,由图1可得:
(1)

图1 基线干涉方法测量原理示意图Fig.1 Baseline interferometer measurement
将此距离差Δr的测量值s作为观测量,建立观测模型,即:

(2)
由此得出分别基于三条基线的距离差的观测方程为:
(3)
可简写成:

(4)

2 航天器轨道动力学方程
在地心赤道惯性系下,考虑地球重心引力,直角坐标形式的轨道运动方程为:

(5)
(6)
在研究过程中,如果将研究对象考虑为二体问题时,即不考虑所有摄动的影响,则:
(7)
式(7)可简写为:

(8)
3 卡尔曼滤波方程
3.1离散型卡尔曼滤波基本原理
由于在导航中所采用的系统模型是系统状态x(t)的非线性函数,所以,要采用非线性滤波方法来估计系统的状态值。EKF算法利用线性化方法将非线性系统近似为局部线性系统,以应用于传统卡尔曼滤波方程,它假设非线性微分方程的理论解与实际解之间的差能用一个线性微分方程表示。
考虑如下形式的随机非线性系统数学模型:

(9)

(10)
式中:x(t)为n维状态向量;f[x(t),t]为n维非线性向量连续函数;G(t)为n×r维矩阵;h[x(t),t]为m维非线性向量连续函数;w(t)和v(t)均为彼此不相关的零均值白噪声序列。
定义真实状态与标称状态间的偏差为:
因为δx足够小,所以将非线性物理系统式(9)和式(10)在状态最优估计附近展开成泰勒级数,并取一次近似值,则可得线性偏差方程为:

(11)

(12)
其中:
对式(11)与式(12)进行基本解阵离散化,得到离散型线性方程为:
(13)
(14)
当T为小量时:
wk-1对应的等效过程噪声方差阵为:

(15)
状态一步预测为:
(16)
状态估计为:
(17)
滤波增益为:
(18)
一步预测均方误差为:
(19)
估计均方误差为:
(20)
3.2量子导航卡尔曼滤波


(21)
其中:
继而离散化得:
(22)
式中:Φk/k-1≈I+F(tk-1)T。
对量子导航的观测方程式(4)进行线性化,得:
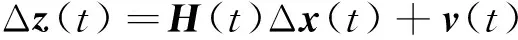
(23)
其中:
继而离散化得:
(24)

4 仿真验证
为了验证卡尔曼滤波对提高量子导航定位精度的有效性,以近地空间航天器的量子导航定位为例进行数学仿真。
4.1仿真条件
星基QPS是由2颗卫星成1条测量基线,基线的两个端点分别对应1颗卫星,3个卫星对分别绕3个低轨地球轨道(LEO)运转,其轨道半长轴a=7 360 km,基线长度b=20 km。3对卫星坐标分别为:
用户端为近地航天器,运动轨道信息为:半长轴a1=7 070 km,偏心率e=1.46×10-7,轨道倾角i=98°,近地点幅角ω=330°,升交点赤经Ω=270°。
4.2仿真结果及分析
采用扩展卡尔曼滤波方法的数值仿真结果如图2~图5所示。由统计结果可知,基于扩展卡尔曼滤波的量子导航位置信息的误差均值为[-3.383,-3.082,5.768]×10-5m,标准差为[8,8,3]×10-4;速度信息的误差均值为[-6.679,-6.357,2.015]×10-4m/s,标准差为[5,5,2]×10-4。

图2 位置分量曲线Fig.2 Position component curves

图3 速度分量曲线Fig.3 Velocity component curves

图4 位置误差Fig.4 Position errors

图5 速度误差Fig.5 Velocity errors
为了更好地分析卡尔曼滤波方法对量子导航定位精度的提高,将量子导航定位模型进行直接解算,得到位置信息的误差均值为[5.879,5.477,-3.281]×10-6m,标准差为[0.0011,0.0010,0.0004]。速度信息的误差均值为[0.185,-3.101,-1.264]×10-4m/s,标准差为[0.0036,0.0321,0.0175]。
对以上统计数据进行对比可以看出,基于EKF的量子导航定位的位置估计是无偏的,标准差有所下降,速度误差标准差有非常明显的下降,这说明了相对于直接进行量子导航定位模型的解算方法,基于扩展卡尔曼滤波的量子导航定位精度有明显提高。
5 结束语
本文给出了量子导航定位中的量测方程,并基于航天器轨道运动方程和量测方程,推导了扩展卡尔曼滤波处理过程。仿真结果表明,相对于未加滤波的量子导航定位系统,基于卡尔曼滤波算法的量子导航定位系统的定位精度有明显提高。
[1]Bahder T B.Quantum positioning system[C]//Washington:Naval Observatory.Washington DC,2005:53-75.
[2]Bahder T B.Quantum positioning system and methods:7359064[P].2008-04-15.
[3]张欢阳,张冠杰,林象平.GPS的未来: 量子定位系统[J].舰船电子工程,2004,24(5):40-43.
[4]雒怡.量子定位技术浅析[J].导航,2004,9(3):11-14.
[5]雒怡,姜恩春.基于二阶量子相干的定位与时钟同步方法[J].现代导航,2012,12(6):456-461.
[6]杨春燕,吴德伟,余永林,等.干涉式量子定位系统最优星座分布研究[J].测绘通报,2009,9(12):1-6.
[7]王恒,李永刚,吴金美.卡尔曼滤波在自旋卫星章动控制中的应用[J].飞行器测控学报,2014,33(6):525-529.
[8]刘爱元,戴洪德.组合导航系统模拟器中的卡尔曼滤波设计[J].计算机与数字工程,2014,42 (9):1649-1652.
(编辑:崔立峰)
Study on Kalman kilter algorithm for the near-earth spacecraft quantum positioning system
WANG Zhi-gang1,2, DENG Yi-fan1,2, YANG Xuan1,2
(1.School of Astronautics, Northwestern Polytechnical University, Xian 710072, China;2.National Key Laboratory of Aerospace Flight Dynamics, Xi’an 710072, China)
In order to improve the precision of spacecraft’s quantum positioning system (QPS), the filter technique was used to combine the QPS observation value with the spacecraft’s motion model to perform filtering estimation of the state variables. The QPS observation equation based on baseline interferometer method and the orbital motion model of the spacecraft was put forward. Furthermore, the process of the extended Kalman filter (EKF) using in this case was derived in detail. The simulation results show that the QPS based on EKF had obvious higher precision than the original one.
quantum navigation; extended Kalman filter; the positioning precision
2015-11-26;
2016-02-29; 网络出版时间:2016-02-29 15:18
航天科技创新基金资助(CASC-1314-05-12)
王志刚(1968-),男,陕西渭南人,教授,博士生导师,博士,主要从事飞行动力学与控制等研究。
V448.23; P228.1
A
1002-0853(2016)05-0069-04

