基于遗传算法的柔性飞翼布局阵风减缓设计
蒲利东, 谭申刚, 霍应元
(中航工业西安飞机设计研究所 强度设计研究所, 陕西 西安 710089)
基于遗传算法的柔性飞翼布局阵风减缓设计
蒲利东, 谭申刚, 霍应元
(中航工业西安飞机设计研究所 强度设计研究所, 陕西 西安 710089)
将飞翼布局飞机的阵风减缓设计转化为多目标优化问题。基于气动伺服弹性稳定裕度修正个体适应度,建立了改进的多目标非支配排序遗传-阵风减缓算法(NSGA-GLA算法)。基于无控飞机的阵风响应特性,提出了阵风减缓控制方案。以翼根弯矩、俯仰角速率和舵偏角最小为目标,采用NSGA-GLA算法对控制器增益参数进行了优化。仿真结果表明,所设计的控制器能够有效改善飞机的阵风响应特性,实现阵风减缓。
飞翼; 阵风减缓; 气动伺服弹性; 多目标遗传算法
0 引言
大型飞翼布局对阵风扰动非常敏感,且其结构弹性振动频率低,对阵风载荷贡献大[1-2]。常规布局飞机采用副翼和扰流板作为直接升力控制面,这种方式可有效实现阵风载荷减缓[3-4]。飞翼布局与之不同,其升降副翼在改变翼面升力分布的同时还会产生较大的俯仰力矩变化。如何确定各控制通道的反馈增益,确保飞机姿态稳定且拥有合理的气动伺服弹性(ASE)稳定裕度的同时,减缓附加阵风载荷,对于飞翼布局实现阵风减缓至关重要。
本文根据某飞翼布局的开环阵风响应特性提出了阵风减缓控制方案,尝试改进多目标遗传算法,优化控制器参数,实现阵风载荷减缓。
1 阵风减缓问题的多目标优化描述
阵风减缓的本质是以最小的控制能量最大限度地减缓附加阵风载荷,同时保证系统拥有合理的稳定裕度,其多目标优化可表达为:
(1)
式中:yi为有控飞机遭遇阵风后的翼根弯矩、翼尖过载等结构响应输出[5];δj为第j个控制面偏角响应;Gmj和Pmj分别为对应于第j个控制通道的幅值和相位稳定裕度[6];X为阵风减缓控制律增益参数列阵;kmin和kmax为增益参数的上、下限值。
2 NSGA-GLA算法
改进的非支配排序遗传算法NSGA-Ⅱ对解决多目标优化问题优势明显[7-8]。针对第1节提出的问题,基于NSGA-Ⅱ算法,利用ASE稳定裕度修正个体适应度,建立NSGA-GLA算法。具体如下:
Step 1: 初始化种群P0, 计算个体目标函数值,并根据个体的幅值和相位裕度设计罚函数,修正个体适应度。
(1)对个体Xm对应的目标函数进行规范化处理:
(2)
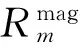
其中:
(3)利用罚函数修正规范化处理后的目标函数,得到个体Xm的适应度:
(4)
Step 2: 将P0中的个体按照其适应度进行非支配排序,计算个体拥挤度。
Step 3: 采用规模为2的随机联赛选择法,根据非支配层级和个体拥挤度,从P0中选择一半的个体组成种群P1。
Step 4: 对种群P1中的个体进行交叉、变异操作,生成个体规模与P0相同的新种群Q0。
Step 5:采用Step 1的方法计算种群Q0中个体的适应度。
Step 6: 种群P0和Q0合并组成新种群Q1,并对Q1中的个体进行非支配排序和拥挤度计算,根据非支配层级和个体拥挤度,从Q1中选择一半的个体组成种群Q2。
Step 7: 判断是否达到终止条件, 若达到,则结束计算;否则令P0=Q2,转到Step 3。
3 阵风减缓设计
3.1开环飞机阵风响应分析
研究对象为后缘布置了三对升降副翼的大展弦比飞翼布局飞机,其最低阶对称弹性振动模态频率为1.5 Hz。选取刚体俯仰和沉浮,以及前20支对称弹性振动模态,利用频域方法[9-10]对开环飞机遭遇Von Karman连续阵风后的响应特性进行了计算,结果如图1所示。
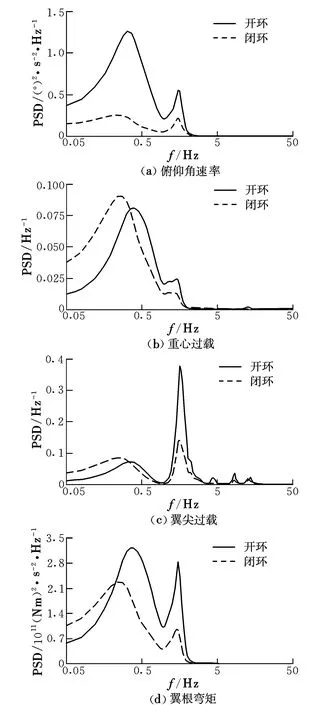
图1 连续阵风响应的功率谱密度Fig.1 PSD characteristics of the aircraft subjected to continuous gust response
对比功率谱密度曲线峰值频率可见,一阶对称弹性振动模态对翼尖过载贡献最大,且其对翼根弯矩及俯仰角速率的贡献亦非常明显。相对而言,弹性振动对重心过载的影响要小很多。
3.2阵风减缓控制方案设计
参考常规布局的飞机直接力控制阵风减缓设计理念[11],每个控制通道均反馈俯仰角速率、翼尖及重心过载共同参与舵偏指令解算,利用优化算法自动调整反馈增益值,以减弱飞翼后缘控制面偏转产生的升力与力矩变化,以及各控制通道之间的耦合效应,如图2所示。同时根据开环飞机各反馈量响应能量随频率的分布关系(见图1)对反馈信号进行滤波,减少非必要频段的结构运动信息进入控制回路,以减弱潜在的不良气动伺服弹性耦合[12-13]。
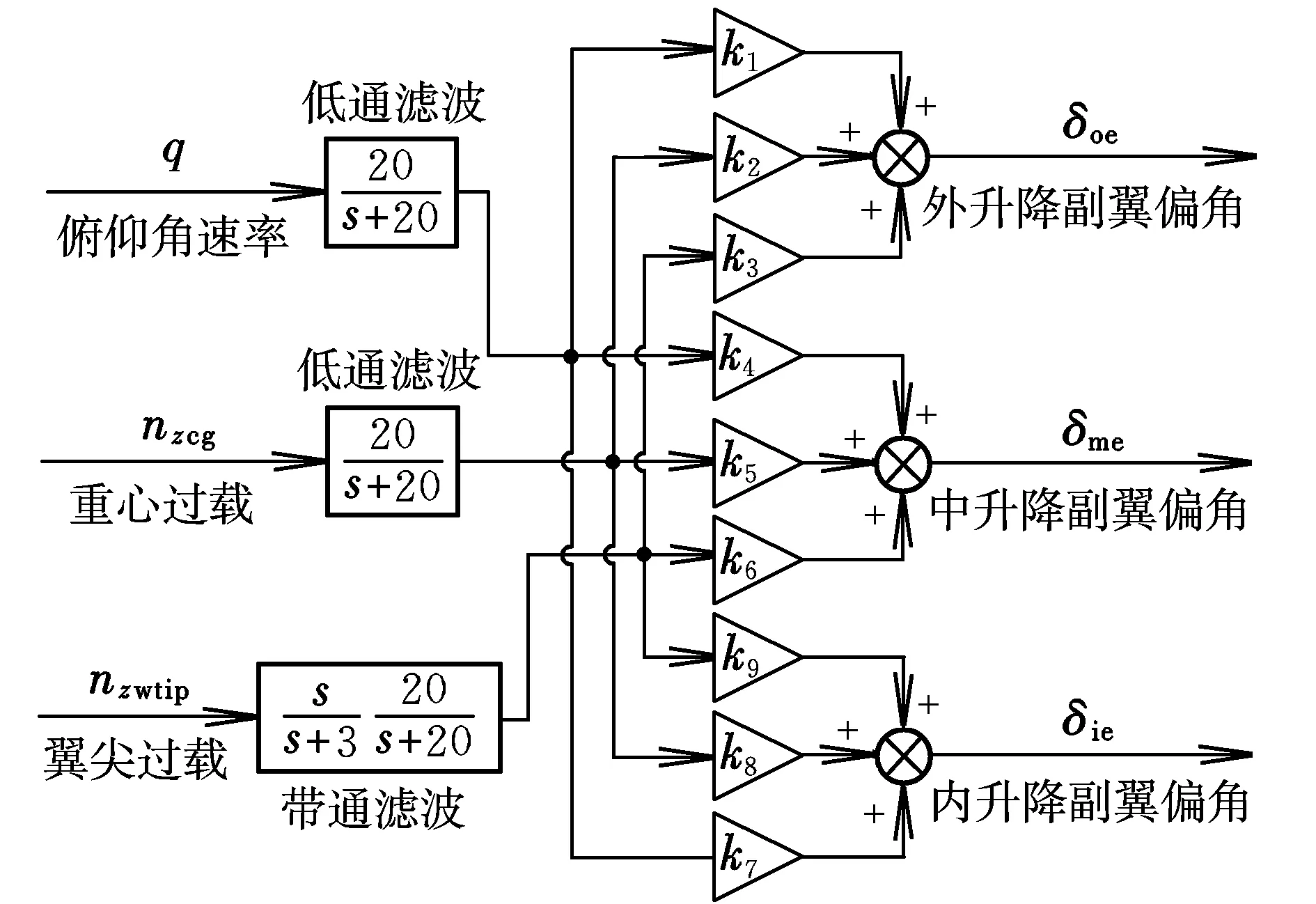
图2 阵风减缓控制方案Fig.2 Gust load alleviation control scheme
3.3阵风减缓控制参数优化
以翼根弯矩均方根σMbend、重心处俯仰角速率均方根σqcg、升降副翼偏角的均方根σδ=max(σδoe,σδme,σδie)最小为目标,采用NSGA-GLA算法计算各反馈增益参数k1~k9的Pareto非劣解。
选取初始种群规模为80,反馈增益的上、下限值分别为3和-3,经120代优化后得到Pareto前沿面,如图3所示。
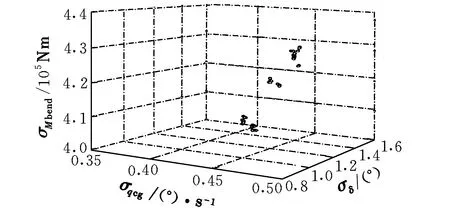
图3 目标函数的Pareto最优解集Fig.3 Pareto optimal solutions for the objective function
4 阵风减缓控制仿真结果及分析
选取Pareto前沿面下端点对应的个体值(k1=-1.2,k2=-3.0,k3=-1.5,k4=1.7,k5=-1.1,k6=-0.2,k7=-0.8,k8=-0.2,k9=1.2)作为阵风减缓控制器的反馈增益,图1和图4分别对飞机遭遇Von Karman连续阵风和1-cos阵风(阵风参数根据GJB 67.2A—2008规定选取)后的响应减缓结果进行了对比。
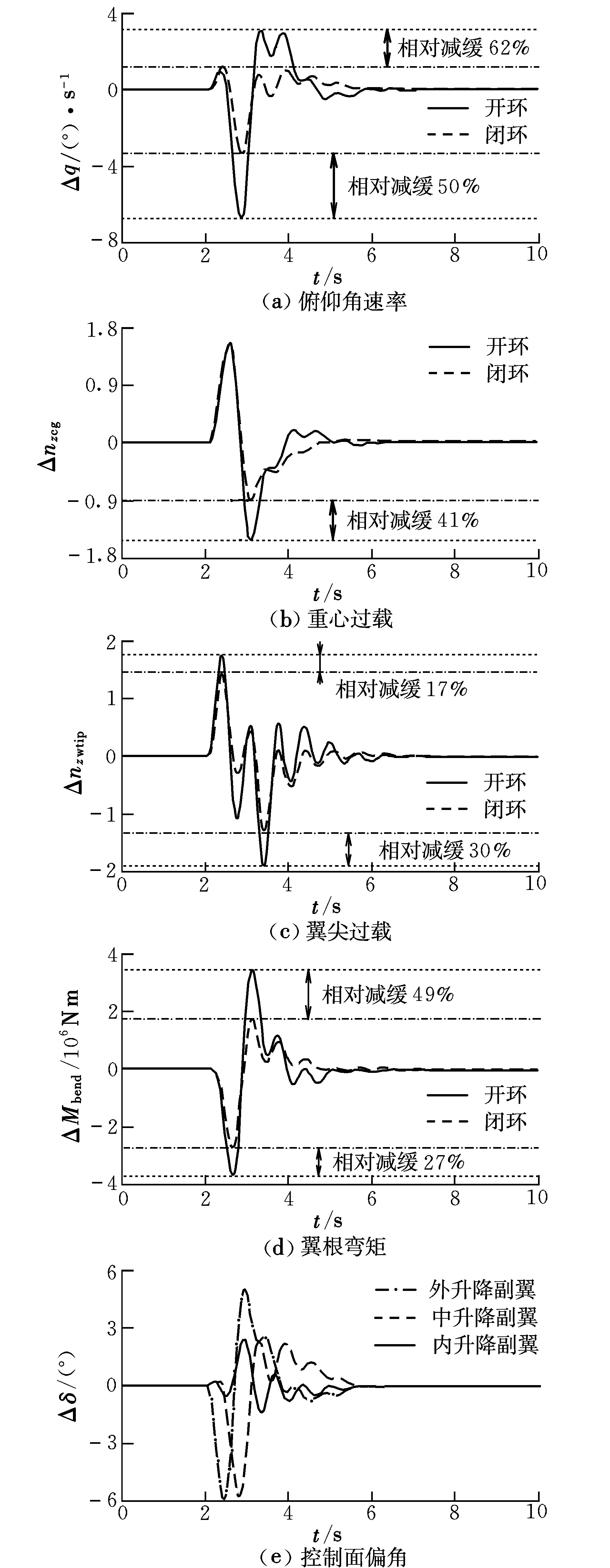
图4 1-cos阵风响应时间历程Fig.4 Response of the aircraft subjected to 1-cos gust responses
由图1可见,一阶对称弹性振动得到了很好的抑制,且刚体频段的俯仰角速率和翼根弯矩响应也得到了有效减缓;虽然翼尖和重心法向过载的响应能量随频率的分布在刚体频段有所增大,但根据设计包线分析准则,闭环状态下的翼尖和重心过载增量还是得到了有效减缓(见表1),这与多目标Pareto最优解的意义并不相悖。图4表明,本文基于连续阵风环境所设计的阵风减缓控制器对1-cos离散阵风同样能够取得很好的减缓效果。

表1 连续阵风载荷增量计算结果
采用Nyquist法[14]计算得出的各控制通道的幅值和相位裕度均满足设计约束,如图5所示。但各控制通道的最大开环响应峰值显然均高于-6 dB。
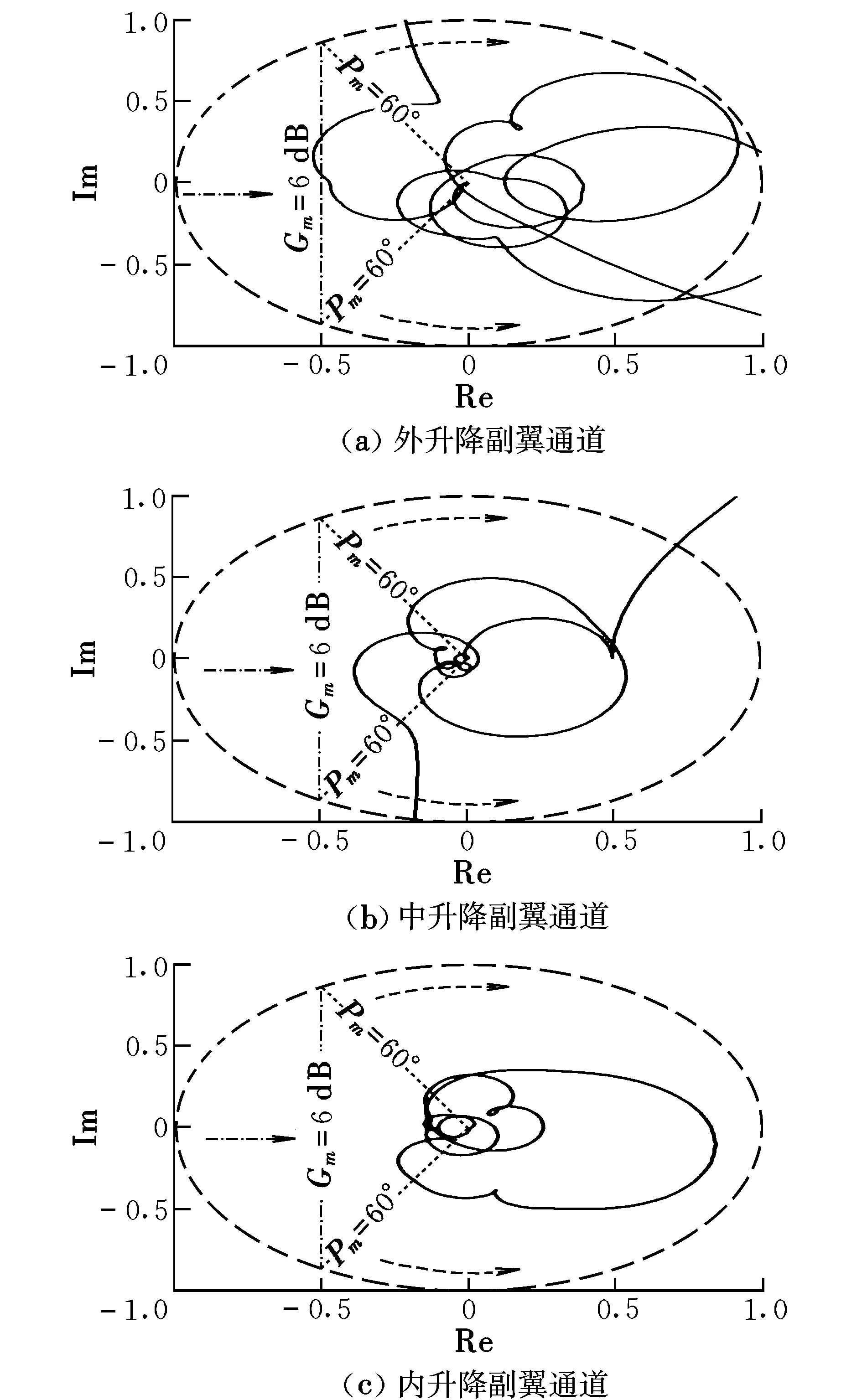
图5 不同控制通道的Nyquist曲线Fig.5 Nyquist curves of the different control channels
对于控制增稳系统,利用结构陷幅滤波器抑制弹性频段的开环响应是提升系统ASE稳定性的有效手段,但这对阵风减缓系统显然不可取。由于必须确保对阵风载荷贡献较大的弹性振动信号参与控制指令解算,方可抑制机体弹性振动以获得满意的阵风减缓效果。因此,飞机模型中对舵偏指令输入到结构响应输出频响特性的模拟必须足够可靠。
5 结束语
将某飞翼布局的阵风减缓设计转换为多目标优化问题,根据开环阵风响应特性,提出阵风减缓控制方案。基于气动伺服弹性稳定裕度修正个体适应度,建立多目标非支配排序遗传-阵风减缓算法优化控制器反馈增益。仿真结果表明,所设计的阵风减缓控制器在保证飞机拥有合理的ASE稳定裕度的同时,能够有效改善飞机的阵风响应特性,实现阵风载荷减缓。
本文在进行阵风减缓设计时并未考虑控制增稳系统的作用,而阵风减缓控制系统对飞机操稳特性的影响不可忽略,下一步将对其进行深入研究。
[1]Britt R T,Jacabson S B,Arthurs T D.Aeroservoelastic analysis of the B-2 bomber[J].Journal of Aircraft,2000,37(5):745-752.
[2]伏欣H W.气动弹性力学原理[M].沈克扬,译.上海:上海科学技术文献出版社,1982:651-652.
[3]费玉华.阵风减缓直接升力控制方案的仿真研究[J].飞行力学,2000,18(1):69-72.
[4]高洁,王立新.大展弦比飞翼构型飞机阵风载荷减缓控制[J].北京航空航天大学学报,2008,34(9):1076-1079.
[5]《飞机设计手册》总编委会.飞机设计手册(第九册):载荷、强度和刚度[M].北京:航空工业出版社,2001:34-38,1234-1248.
[6]Arthurs T D,Gallagher J T.Interaction between control augmentation system and airframe dynamics on the YF-17[R].AIAA-75-0824,1975.
[7]Kalyanmoy Deb,Amrit Pratap,Meyarivan T.A fast and elitist multi-objective genetic algorithm NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[8]赵亮,雎刚,吕剑虹.一种改进的遗传多目标优化算法及其应用[J].中国电机工程学报,2008,28(2):96-101.
[9]Rodden W P,Johnson Erwin H.MSC/NASTRAN aeroelastic analysis user’s guide version 68[M].Los Angeles:The Macneal-Schwendler Corporation,1994:67-76.
[10]杨超,吴志刚,万志强,等.飞行器气动弹性原理[M].北京:北京航空航天大学出版社,2011:130-147.
[11] 袁刚,李爱军,王长青,等.多舵面大型民机阵风减缓系统设计[J].飞行力学,2011,29(4):65-67.
[12]Wykes J H,Mori A S,Borland C J.B-1 structural mode control system[R].AIAA-72-0772,1972.
[13]Wykes J H,Klep M J,Brosnon M J.Flight test and analyses of the B-1 structural model control system at su-personic flight conditions[R].NASA-CR-170405,1983.
[14]陈桂彬,邹丛青.气动伺服弹性技术在飞机设计中的应用[J].航空学报,1996,17(7):31-35.
(编辑:姚妙慧)
Gust load alleviation of a flexible flying wing configuration based on genetic algorithm
PU Li-dong, TAN Shen-gang, HUO Ying-yuan
(Strength Design and Research Institute, AVIC Xi’an Aircraft Design Institute,Xi’an 710089, China)
The multi-objective genetic algorithm was used to the gust load alleviation control of a flying wing configuration. The fitness function was corrected and an improved Non-Dominated Sorting Genetic-Gust Loads Alleviation Algorithm (NSGA-GLA) was developed based on the aeroservoelastic stability margin. Based on the open-loop gust response characteristics, gust load alleviation control scheme was designed, and the feedback gains of the controller were optimized to minimize the wing bending moment, the pitch rate and the control surface deflection. The results show the feasibility of the scheme and the effectiveness of the controller in gust load alleviation.
flying wing; gust load alleviation; aeroservoelastic; multi-objective genetic algorithm
2015-10-22;
2016-02-16; 网络出版时间:2016-04-22 09:52
国家科技部国际合作专项基金资助(2013DFA80710)
蒲利东(1984-),男,甘肃会宁人,高级工程师,硕士,主要从事气动弹性主动控制研究。
V215.3
A
1002-0853(2016)05-0040-04

