金属带锯床锯切进给过程建模与分析
倪 敬,李 璐,郎建荣
(杭州电子科技大学机械工程学院,浙江 杭州 310018)
金属带锯床锯切进给过程建模与分析
倪敬,李璐,郎建荣
(杭州电子科技大学机械工程学院,浙江 杭州 310018)
金属带锯床锯切进给过程的研究对实现锯切负载预测与精确锯切控制有着至关重要的作用,其中进给液压驱动和摩擦导致的爬行现象尤其需要研究并解决.针对金属带锯床液压驱动锯切进给系统,首先,通过阀控非对称缸的非线性动力学分析,建立了锯切进给过程的锯架液压驱动的动力学模型;其次,结合Stribeck摩擦模型,建立了进给液压缸活塞与内壁间的非线性摩擦力模型;最后,综合两部分模型,提出了金属带锯床锯切进给过程的非线性动力学模型.仿真和锯切进给实验表明,提出的模型较好地描述了锯切进给过程,并给出了产生爬行现象的条件.
金属带锯床;锯切进给;爬行现象;Stribeck摩擦模型
0 引 言
高效的金属带锯锯切技术广泛应用于金属和非金属材料的加工行业[1],因其锯切进给过程受到液压驱动系统和摩擦等非线性影响,不易被实时检测和补偿,这些一直是锯切负载预测与精确锯切控制中的难点[2].如何准确描述带锯床锯切进给过程的非线性动态特性,研究并发现液压驱动和摩擦特性导致的爬行现象,以便更有效地预测锯切负载,提高锯切过程的可靠性以及加工精度,是带锯行业中亟待解决的问题之一.
对于金属带锯床的进给特性,国内外学者进行了大量地研究.文献[3]将锯切视作多点切削,在建模与仿真中将进给速度视为匀速,提出了经典锯切负载模型;文献[4]通过实验研究了带锯床锯架进给速度与加工后工件表面质量的关系;文献[5]针对带锯床进给速度的实时检测和补偿问题,建立了神经模糊控制系统;文献[6]通过实验研究了锯切不同材料、不同尺寸的工件下应该选取的最佳进给速度;文献[7]基于哈密顿原理,研究了带锯切削过程中的振动与应力;文献[8]研制了一种带锯床恒功率锯切系统,并建立了带锯条空载数学模型和锯齿锯切负载模型;文献[9]认为被切工件的截面尺寸和形状发生变化时,带锯床的进给系统无法对速度进行相应调整,即切削时进给速度恒定不变;文献[10]对带锯锯切力的计算、锯切过程的力学模型、带锯床的动态特性以及带锯床的可靠性设计方法等进行了研究.然而上述文献涉及的研究内容与实验,都将带锯床的进给视为一种匀速进给运动,忽略了带锯床进给的非线性动态特性,没有较详细地描述具体进给过程.为此,本文提出了一种金属带锯床锯切进给过程的非线性动力学模型,并进行了分析与验证.
1 系统模型
金属带锯床系统结构如图1所示,主要由进给液压缸、进给导向柱、夹紧液压缸、主动带轮、从动带轮、带锯条、锯架、控制柜等组成.具体工作原理为:带锯条张紧在主动带轮和从动带轮上,并由主动轮驱动实现带锯条的往复式锯切运动;锯架由进给导向柱和进给液压缸支撑,并由进给液压缸驱动实现带锯条的锯切进给运动.
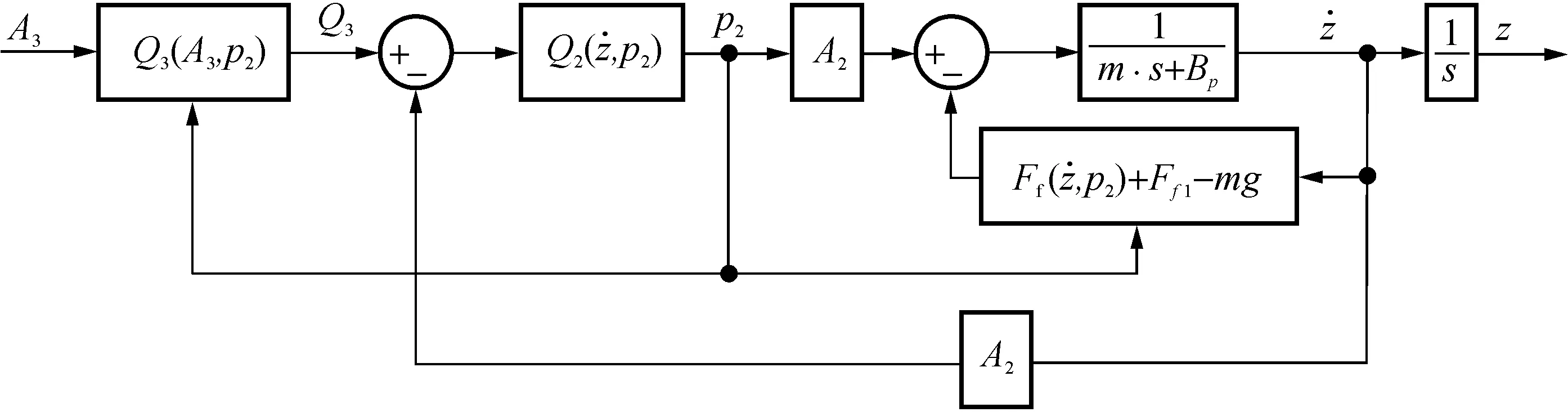
具体金属带锯床进给系统驱动液压原理如图2所示,主要包括油源、电磁换向阀、节流阀等.其中,电磁换向阀1和节流阀3控制进出进给液压缸无杆缸的油液流动速度,实现带锯床锯切进给过程的向下工进运动和向上退刀运动,工进速度由节流阀3的阀口面积调定;电磁换向阀2实现带锯床锯切进给过程的向下快速工进运动,此时无杆腔与油源相通.图2中,z为锯架进给位移量,单位为mm;m为锯架及进给液压缸活塞整体重量,单位为kg;g为重力加速度,单位为m/s2;F为进给液压缸对锯架的支撑力,单位为N;Ff为进给液压缸对锯架的摩擦力,单位为N;Ff1为锯架与进给导向柱的摩擦力,单位为N;p1为进给液压有杆腔油液压力,单位为Pa;A1为进给液压缸有杆腔的有效作用面积,单位为mm2;p2为无杆腔油液压力,单位为Pa;A2为无杆腔的有效作用面积,单位为mm2;A3为节流阀3的流通面积,单位为mm2.
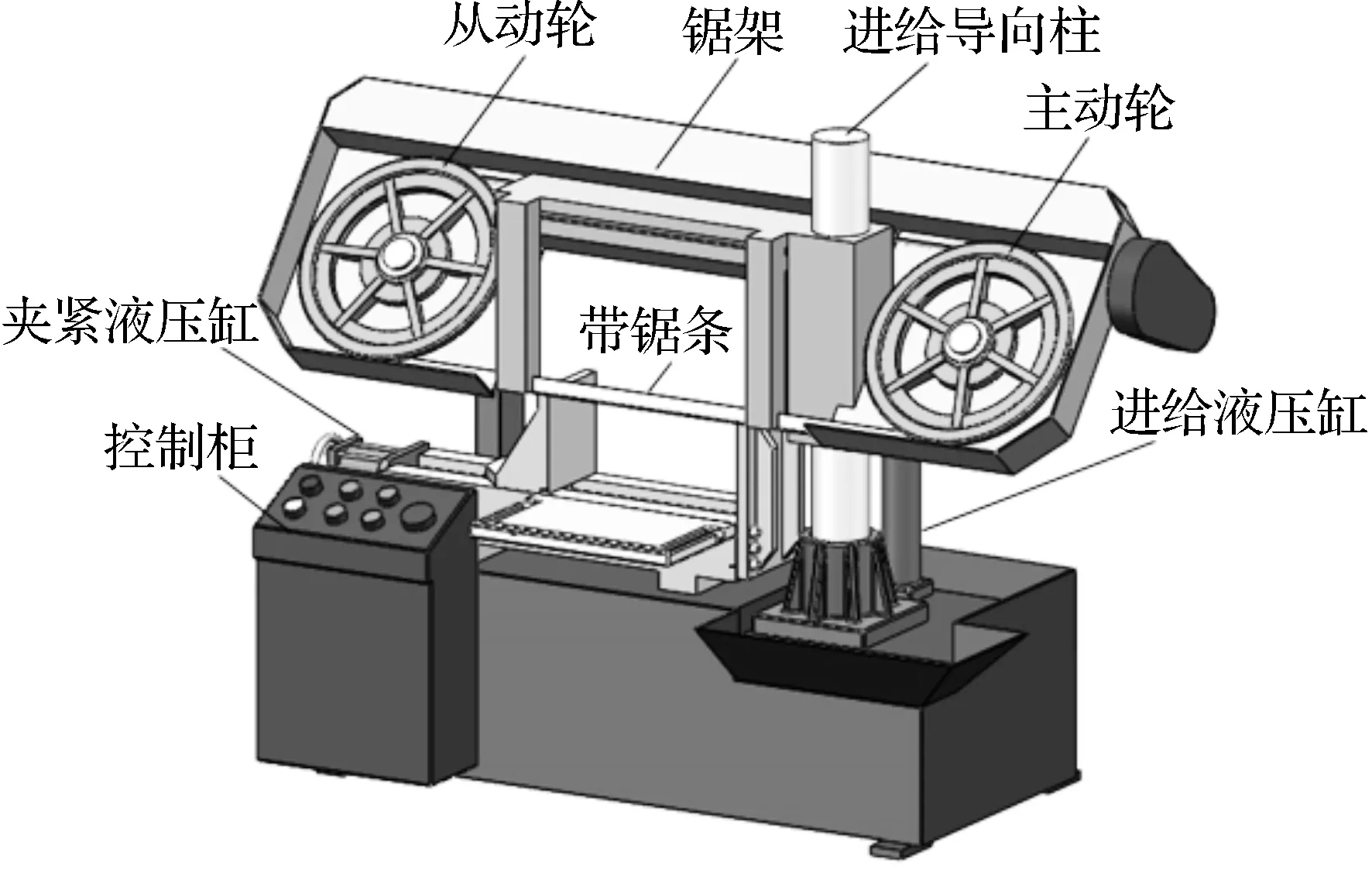
图1 金属带锯床结构图
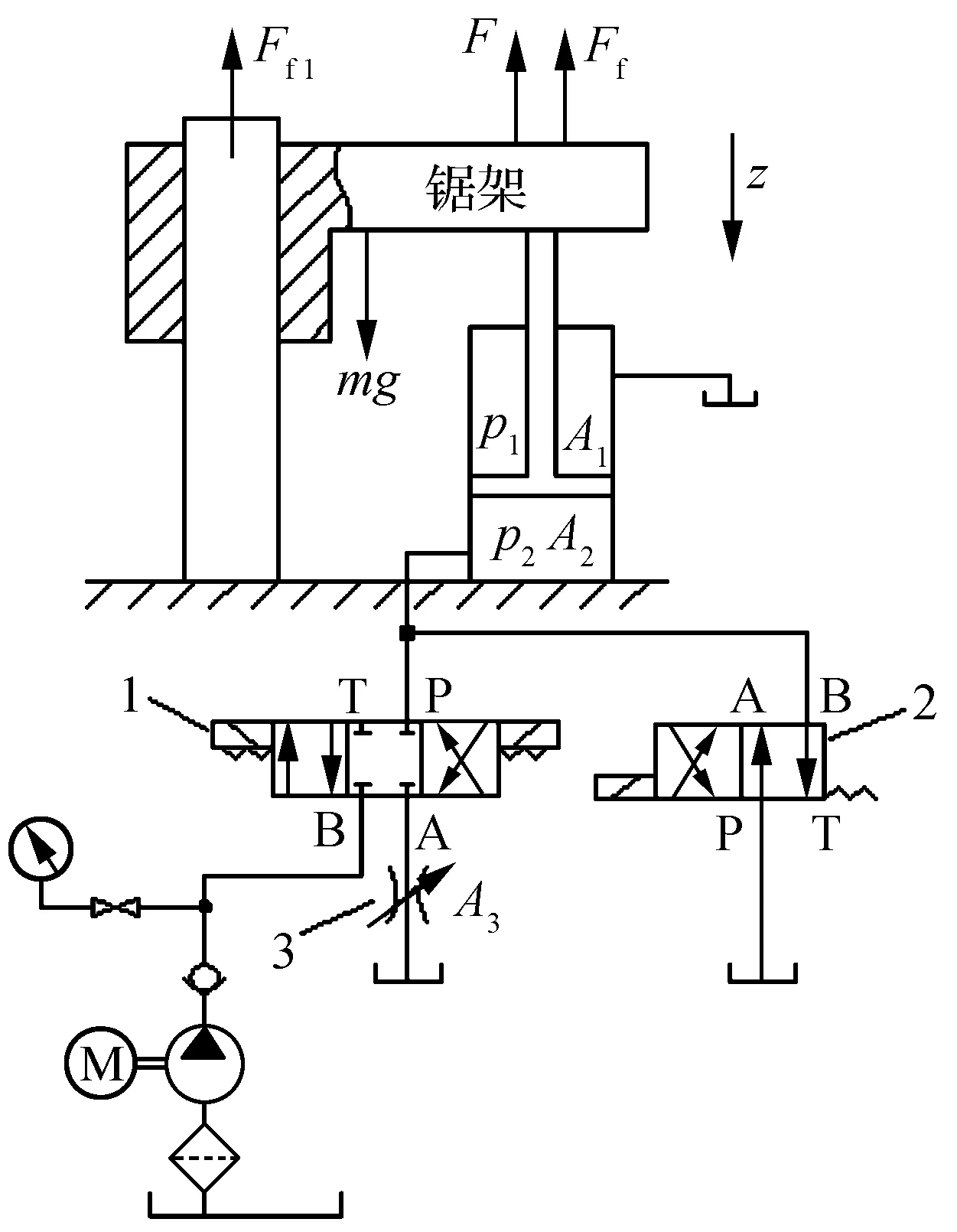
图2 带锯床进给系统简化模型
1.1锯架液压驱动的动力学模型
如图1带锯床结构图所示,进给导向柱与进给液压缸中心距离较小,且锯架与导向柱之间导向距离较长,为此,锯架对进给液压缸的活塞弯矩很小,可以忽略不计.此外,进给液压缸有杆腔与油箱相通,故p1≈0.
这样,以图2的锯架和进给液压缸活塞杆为研究对象,根据牛顿第二定律有:
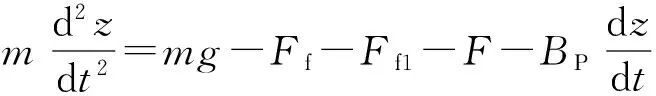
(1)
式中:Bp为液压缸活塞的粘性阻尼系数,单位为N·s/m.
进给液压缸对锯架的支撑力F可以描述为:
F=A2p2-A1p1.
(2)
以进给液压缸的无杆腔为研究对象,其流出无杆腔的流量Q2的可以描述为:
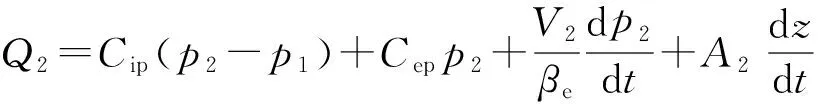
(3)
式中:Cip为液压缸的内泄系数,单位为m5/(N·s);Cep为液压缸的外泄系数,单位为m5/(N·s);βe为油液容积模数,单位为MPa;V2为液压缸无杆腔所有液体容积,单位为mm3,V2=A2(LS-z),LS为液压缸的行程,单位为mm.
以节流阀为研究对象,通过节流阀的流量Q3可以表示为:
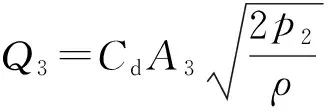
(4)
式中:Cd为阀流量系数;ρ为液压油密度,单位为kg/cm3.
根据流量连续性原理,液压缸无杆腔流量与通过节流阀的流量应该相等,即
Q2=Q3.
(5)
于是,由式(1-5),得到锯架液压驱动的动力学模型如下:
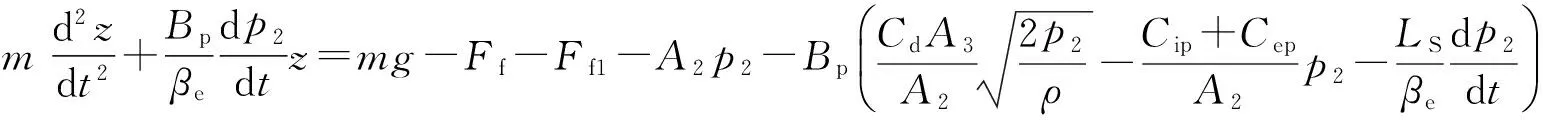
(6)
从式(6)可以看出,研究锯架进给过程的非线性动特性,除了要考虑液压系统动特性(Bp,βe,Cip,Cep等),还必须考虑液压系统中进给液压缸的摩擦力特性(Ff).
1.2进给液压缸摩擦力建模
根据实际锯切进给工况,锯架的运动速度一般在0~50 mm/s之间,属于低速运动范畴.在这种工况下,锯切进给运动过程中进给液压缸的摩擦特性将出现如图3所示的Stribeck效应[11].
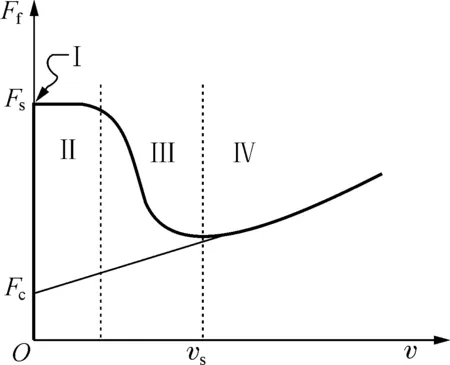
图3 Stribeck摩擦模型
该摩擦效应主要包括4个区域:干摩擦或近于干摩擦区(I区)、边界润滑区(Ⅱ区)、混合润滑区(Ⅲ区)、弹性流体动力润滑区(Ⅳ区).各区的建模详细描述如下:
1)干摩擦或近似干摩擦区(I区)
锯架静止不动时,即dz/dt=0,进给液压缸活塞与内壁接触面间由于润滑油液的挤出,而呈现干摩擦或近于干摩擦状态.此时锯架所受的摩擦力主要为静摩擦力,具体静摩擦力Ffp可表示为:
(7)
式中:Fs为最大静摩擦力,单位为N.
2)边界润滑区(II区)及混合润滑区(III区)
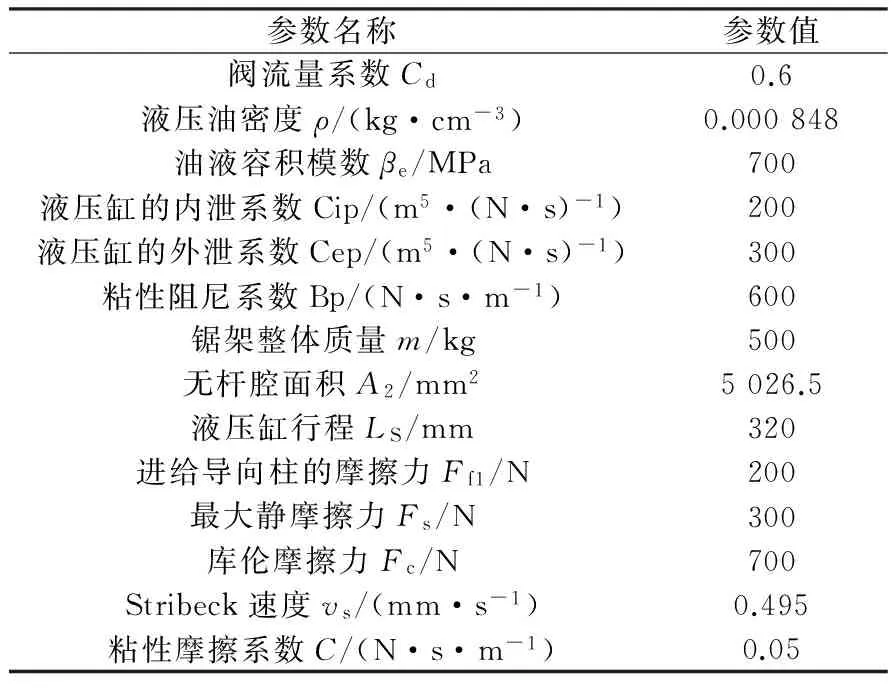
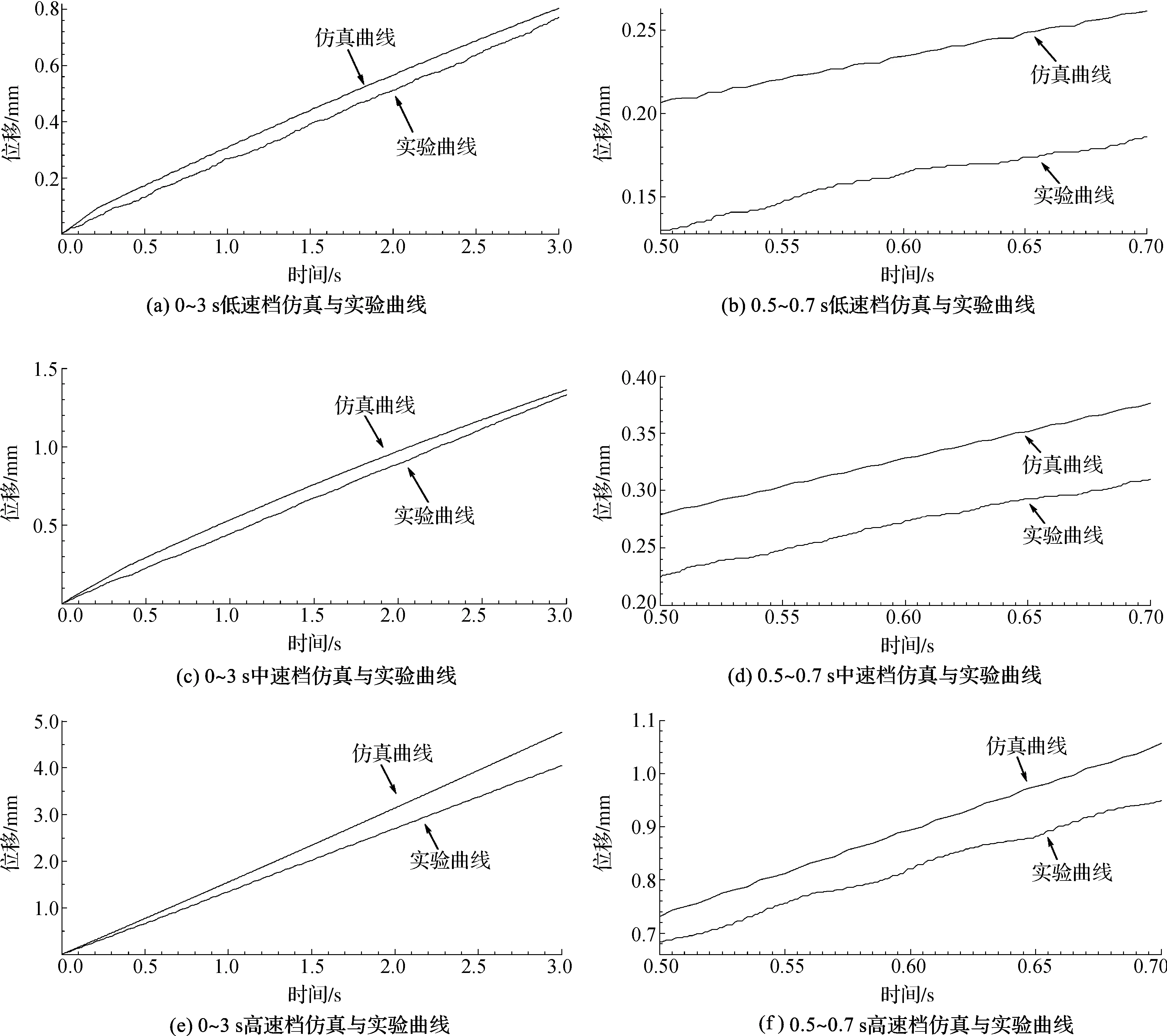
锯架开始运动后,润滑液不断增加,进给液压缸活塞与内壁接触面间进入边界润滑区(Ⅱ区).但由于进给速度较低,接触面间还无法建立起动压润滑油膜,此时的载荷全部由接触面微凸体接触承受,摩擦力也较大.随着锯架运动速度继续增大,活塞与内壁部分动压润滑油膜开始建立,润滑状态由边界润滑区逐渐过渡到混合润滑区(Ⅲ区),摩擦力迅速下降.即0 (8) 式中:Fc为库仑摩擦力,单位为N;vs为Stribeck速度,混合润滑区向弹性流体动力润滑区过渡的临界速度,单位为mm/s;C为粘性摩擦系数,单位为N·s/m. 3)流体润滑区(IV区) 随着锯架进给速度继续增大,到达某个数值范围后,液压缸活塞与内壁间建立起润滑油膜,从而摩擦进入到流体润滑区(Ⅳ区).即dz/dt>vs时,摩擦力随速度增加而增大,其具体动摩擦力Ffs可表示为: (9) 综上所述,基于Stribeck效应的进给液压缸活塞与内壁间非线性摩擦力模型可表示为: (10) 1.3金属带锯床进给过程的非线性动力学模型 根据上述分析,将式(10)的摩擦力模型代入式(6),整理得到从节流阀阀口面积到给进给液压缸活塞位移的非线性数学模型如图4所示. 图4 金属带锯床进给非线性数学模型 从图4描述的模型可以清晰地看出,进给系统的非线性动特性主要来自于节流阀口流量特性Q3和液压缸无杆腔的流量特性Q2,以及进给液压缸活塞与内壁之间的摩擦特性Ff. 2.1实验系统 金属带锯床进给实验系统如图5所示.实验机床为G4230-50型卧式金属带锯床,其主电机功率3 kW,额定转速1 440 rpm,进给液压缸活塞直径80 mm,活塞杆直径56 mm,行程320 mm,三位四通电磁换向阀型号4WE6E-61/EG24NZ5L,两位四通电磁阀型号4WE6D-61/EG24NZ5L,节流阀型号L-10,位移传感器采用美国MTS的SSI输出型磁致伸缩位移传感器,分辨率0.001 mm,频率响应时间为1 ms,数据采集硬件为研华610L工控机与西门子S7-300PLC系统,数据分析软件为BCB软件和MATLAB软件.具体锯架进给系统的仿真参数取值如表1所示. 表1系统仿真参数表 参数名称参数值阀流量系数Cd0.6液压油密度ρ/(kg·cm-3)0.000848油液容积模数βe/MPa700液压缸的内泄系数Cip/(m5·(N·s)-1)200液压缸的外泄系数Cep/(m5·(N·s)-1)300粘性阻尼系数Bp/(N·s·m-1)600锯架整体质量m/kg500无杆腔面积A2/mm25026.5液压缸行程LS/mm320进给导向柱的摩擦力Ff1/N200最大静摩擦力Fs/N300库伦摩擦力Fc/N700Stribeck速度vs/(mm·s-1)0.495粘性摩擦系数C/(N·s·m-1)0.05 图5 锯切进给实验系统图 2.2实验方案设计 为验证金属带锯床的锯切进给过程模型与实际结果,具体安排的实验方案如表2所示. 表2 实验方案 2.3实验与仿真结果分析 根据实验方案,具体锯架的进给过程实验与仿真结果如图6所示,图6中横轴为时间,纵轴为金属带锯床锯架进给的位移.如图6所示,由于开始的0~3 s内锯架的进给过程最为不稳定,因此选取0~3 s作为主要分析的时间段,分别对应图6中(a),(c),(e),并从中随机抽取0.5~0.7 s的时间段进行放大分析,分别对应图6中(b),(d),(f). 图6 实验结果与仿真 分析实验与仿真,得到以下结论: 1)3种工况下仿真与实验的锯架进给过程平均速度va和进给最大间歇时间tm(锯架进给运动中最长静止时间)对比如表3所示.从表3的数据对比可以看出,每一个工况下仿真与实验结果较为吻合.因此,本文提出的模型较好地描述了锯切进给过程中的非线性动态特性. 表3 锯架进给过程仿真和实验结果对比 2)锯架的进给过程呈现较明显的爬行现象.通过表3中进给最大间歇时间tm的仿真值与实验值可以看出,锯架的进给过程呈现较明显的爬行现象.由于锯架液压驱动的非线性特性以及液压缸非线性摩擦特性,金属带锯床在工进时呈现出爬行现象,即间歇性进给运动,并非匀速进给.这主要是由于锯架运行过程中液压缸摩擦特性与进给速度相互耦合,导致带锯床的速度在Stribeck模型的4个区内交替变化,所受摩擦力随之变化,最终呈现出爬行现象. 3)锯架进给过程的Stribeck效应随着进给速度降低而增强.从图6(b)、(d)、(f)的仿真与实验曲线,以及表3中最大间歇时间的仿真值与实验数值可以得到,随着进给速度的降低,最大间歇时间变长,即驱动特性与摩擦特性对锯架进给运动的影响随着进给速度的降低而增强. 4)锯架进给过程的速度存在较大波纹.从图6(b)、(d)、(f)中可以看出,即使当摩擦处于流体润滑区时,尽管不再产生爬行现象,但此时速度也会由于摩擦力大小的变化产生明显波动,形成较大的速度波纹. 本文考虑摩擦影响的金属带锯床锯切进给过程,建立了锯切进给过程的非线性动力学模型.通过仿真计算与实验验证相结合的方法,验证了模型的有效性,并揭示了产生锯架进给过程爬行现象的条件.金属带锯床锯切进给过程的深入研究对实现带锯床锯切负载的预测和恒功率锯切,以及提高工业生产中带锯条使用寿命、加工精度都具有重要的理论与实际意义. [1]SARWAR M,PERSSON M,HELLBERGH H, et al.Measurement of specific cutting energy for evaluating the efficiency of bandsawing different workpiece materials[J].International Journal of Machine Tools and Manufacture,2009,491(12):958-965. [2]NI J, XIA Z N. Adaptive generalized predictive control on electro hydraulic servo feeding system of band saw[J].Applied Mechanics and Materials,2013,433-435:1947-1952. [3]KO T J, KIM H S. Mechanistic cutting force model in band sawing[J].Journal of Machine Tools and Manufacture,1999,39 (8):1185-1197. [4]OKAI R.Influence of vibration coupling between bandsaw frame and feed-carriage system on sawdust spillage and surfacequality of workpiece during sawing[J].European Journal of Wood and Wood Products,2009,67(2):189-195. [7]GENDRAUD P, ROUX J C, BERGHEAU J M. Vibrations and stresses in band saws:A review of literature for application to the case of aluminium-cutting high-speed band saws[J]:Journal of materials processing technology,2003,135(1):109-116. [8]蒙臻.带锯床恒功率锯切系统研制[D].杭州:杭州电子科技大学,2013. [9]曾芸.卧式金属带锯床进给系统设计与研究[D].长沙:中南大学,2006. [10]韩斌.金属切削带锯床设计的若干问题研究[D].杭州:浙江工业大学,2012. [11]ARMSTRONG-HÉLOUVRY B,DUPONT P,DE WIT C C.A survey of models,analysis tools and compensation methods for the control of machines with friction[J].Automatica,1994,30(7):1083-1138. Modeling and Analysis of Band Saw Feeding Process with Friction NI Jing, LI Lu, LANG Jianrong (SchoolofMechanicalEngineering,HangzhouDianziUniversity,HangzhouZhejiang310018,China) The performance of the feeding process has a crucial effect on both cutting force forecasting an accurate control for metal bandsaw machine. The characteristics such as friction and hydraulic drive of the feeding process can cause the stick-slip phenomenon. According to the feeding system of the metal band sawing machine with hydraulic drive, the dynamics model of the saw frame with hydraulic drive is established firstly based on the nonlinear dynamics analysis of valve-controlled asymmetrical cylinder. Secondly, the nonlinear fiction model between the hydraulic cylinder piston and inner wall is established combining the Stribeck friction model. Finally, synthesizing the forward two models, the nonlinear dynamics model of metal band sawing machine during the feeding process is proposed. Results of simulation and experiment show that the proposed model well descripts the feeding process, and presents the generation conditions of the stick-slip phenomenon. metal bandsaw machine; saw feeding; stick-slip phenomenon; Stribeck friction model 10.13954/j.cnki.hdu.2016.05.012 2015-12-17 国家自然科学基金资助项目(51375129) 倪敬(1979-),男,浙江武义人,教授,金属带锯锯切技术. TH113.2 A 1001-9146(2016)05-0062-06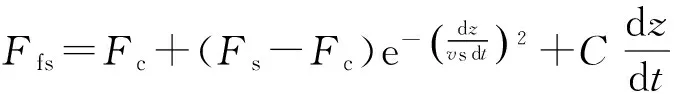
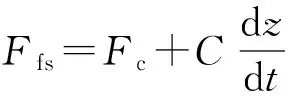
2 金属带锯床进给实验与分析



3 结束语

