例谈相遇问题在初中数学中的应用

沈卫军

摘 要：在苏科版七年级数学上第四章第3节“用一元一次方程解决问题”中，有一类关于行程问题的应用题中，相遇问题是常见的一类题目，它贯穿于整个初中数学阶段，在不等式、函数中都出现了它的身影，而且方程、不等式、函数之间有着很密切的关系。就通过几个例题来谈一谈相遇问题在初中数学中的应用。

关键词：相遇；时间；速度；路程

有关相遇问题的题目从七年级上的一元一次方程中首次出现，一直到九年级中的函数也有相关问题，在中考中也是常见的一种题型，因此，本文就通过几个例题，由浅入深，来谈谈相遇问题在初中数学中的应用。

【例1】甲、乙两辆汽车分别从相距270千米的A、B两地同时相向而行，已知甲车的速度为每小时行40千米，乙车的速度为每小时行50千米，问出发后多长时间两车相遇？

解析：此题中关键是抓住相遇问题中甲、乙两辆汽车行驶时间相等，甲乙两辆汽车行驶的路程之和等于A、B之间的路程即可，如果能画出线段图（如下图），那么问题就能迎刃而解：设出发后x小时相遇，可得方程40x+50x=270，解之得x=3，即出发后3小时两车相遇。

这是最基础的相遇问题，解决这类应用题，关键是能画出线段示意图，特别是一些稍复杂的题目，分析出整段行驶的过程，理清时间、速度、路程之间的关系，这一类相遇的问题便能迎刃而解。

【例2】小明和爸爸同时从距离20千米的两地相向而行，爸爸每小时走6千米，小明每小时走4千米，小明带着只狗，狗每小时跑10千米，这只狗和小明同时出发，碰到爸爸的时候，马上掉头朝小明这边跑，碰到小明的时候又掉头朝爸爸方向跑去，直到小明和爸爸相遇，问这只狗一共跑了多少千米？

解析：此题是多次相遇的问题，但本题中并不需要知道相遇了几次，求狗一共跑了多少千米，因为狗的速度已知了，所以只要知道狗跑的时间就可以了，而狗跑的时间和小明、爸爸跑的时间是相同的，而这个时间就是小明和爸爸相遇所需的时间，从而又转化到例题1中的相遇问题了。

解：设小明和爸爸相遇的时间为x小时。

由题意得：6x+4x=20

x=2

即狗跑了2小时，所以狗一共跑了2×10=20千米

但有些题目中并不是同时出发，或者说他们行驶的时间是不相等的，那这一类相遇的行程问题又该如何解决呢？那我们就通过下面的例题来看看。

【例3】甲、乙两辆汽车分别从相距270千米的A、B两地同时相向而行，已知甲车的速度为每小时行40千米，乙车的速度为每小时行50千米，甲车刚出发就因汽车抛锚而耽搁了半小时，问乙车出发多少小时后两车相距20千米？

此题中甲车中途停留了半小时，所以这半小时，甲车没前进，所以在计算路程时应当注意，但不管是停留还是有些题目中谁先出发，我们都应该抓住甲乙两车行驶的路程等于整段路程这一等量关系，本题还应注意两车相距20千米有两种情况，第一种情况（如下图1）：两车还没相遇之前相距20千米，根据“甲车行驶的路程+乙车行驶的路程=A、B之间的距离-20千米”这一等量关系，设出发x小时之后，两车在相遇前相距20千米，得方程：50x+40（x-0.5）=270-20，解得x=3，第二种情况（如下图2）：两车相遇之后继续往前走，相距20千米，根据“甲车行驶的路程+乙车行驶的路程=AB之间的距离+20千米”这一等量关系，设出发后y小时两车相遇后相距20千米，得方程：50y+40（y-0.5）=270+20，解得y=31/9，因此乙车出发后3小时或31/9小时后两车相距20千米。

对于这种不管是中间停留还是谁先出发的题型，同样我们应该通过画线段图，找出他们路程之间的关系，只不过行驶的时间现在不相等了，这些都是相遇问题在方程中的应用，在其他章节中同样也出现过相遇问题，下面我们就继续来看看。

【例4】A、B两地相距270千米，两地之间有个C站，甲车由A地驶往C站，乙车由B地驶往C站，两车同时出发，本来约定3个小时能同时到达C站，但因甲车刚出发半小时，因汽车抛锚而花了半小时修车，已知甲车原来的速度为40千米/小时，问甲车为了能赶在B车到达C站之前到达C站，甲车修好车之后的速度应不低于多少？

此题中乙车的路程不变，速度不变，到达C站的时间也不变，所以关键是甲车修好车之后行驶的那一段路程，甲车出发半小时，修车半小时，也就是说修好车之后赶去C站的时间最多2小时，路程不变，由此才会有问题中甲车速度应不低于多少，此题可由“约定3小时同时到达C站”，求出AC之间的距离为40×3=120千米，则修好车之后甲车距C站还有120-40×0.5=100千米，设甲车的速度应不低于x千米/小时，可得不等式x/100≤2，解得x≥50，即甲车的速度应不低于50千米/小时。

这个是相遇问题在不等式中的应用，我们现在应该重点抓住他们在行驶过程中路程、速度或者时间之间的不等关系来列出不等式，从而解决问题。下面我们通过最后一个例题来看一看相遇问题在其他方面的应用。

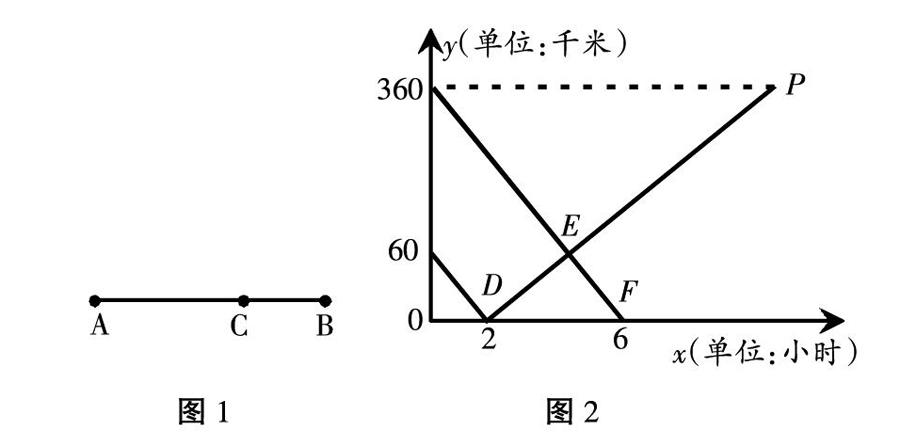
【例5】如下图1所示，在A，B两地之间有汽车站C站，客车由A地驶往C站，货车由B地驶往A地.两车同时出发，匀速行驶.图2是客车、货车离C站的路程y1，y2（千米）与行驶时间x（小时）之间的函数关系图象。

（1）填空：A，B两地相距_____千米；

（2）求两小時后，货车离C站的路程y2与行驶时间x之间的函数关系式；

（3）客、货两车何时相遇？

解析：（1）由题意可知：B、C之间的距离为60千米，A、C之间的距离为360千米，A，B两地相距360+60=420千米；

（2）根据货车两小时到达C站，求得货车的速度，进一步求得到达A站的时间，进一步设y2与行驶时间x之间的函数关系式可以设x小时到达C站，列出关系式，代入点求得函数解析式为y2=30x-60即可；

（3）两辆车相遇在函数图象中就是两函数的图象相交，求得y1的函数解析式，与（2）中的函数解析式联立方程，解决问题。

关键我们来看看第（3）小题，这就是相遇问题在函数中的应用，两车相遇在函数图象中就是两直线相交，从而我们可以通过列方程组来求两直线的交点，从而求得相遇的时间。

函数是初中数学中的一个重点和难点，也是中考中的一个热点考题之一，综合性比较强，解题的关键是根据题意结合图象说出其图象表示的实际意义，这样便于理解题意及正确解题。

以上就是我通过几个例题来看看相遇问题在初中数学中的应用，我们应该理清它们之间的内在联系，在平时的教学过程中，特别是初三复习中要加强训练，知识点与知识点之间加强联系，做到一题多变。以上就是我自己的一些观点，如有不足之处，希望各位专家和同仁指教。

编辑 谢尾合