基于覆盖粗糙集的超图连通性

黄爱萍,黄凤英



基于覆盖粗糙集的超图连通性

黄爱萍*,黄凤英

（厦门大学嘉庚学院信息科学与技术学院，漳州363105）

作为图论的推广，超图已被广泛应用于数据挖掘领域。在此领域中，超图常被用于模拟数据之间的结构特征；又因为该领域中的数据通常表现为覆盖的形式，而覆盖粗糙集为此类数据的研究提供了系统的方法。鉴于此，本文将覆盖粗糙集与超图联系起来，利用覆盖粗糙集的方法研究了超图的连通性。首先，由超图诱导出一个覆盖；其次，利用该覆盖上的近似算子研究超图的连通性。结果表明，覆盖粗糙集为研究超图提供的一种新的方法。

覆盖粗糙集；超图；超图连通性

引言

图是描述计算机科学，物理，数学等学科中问题及结构的强有力工具。但因为只能模拟一些二元关系，这往往不能满足人们模拟现实生活中遇到的一些复杂的问题或者数据。为了解决这一问题，C.Berge[1]于1960年将图进行推广，建立了超图理论。此理论视集合为超边，而超图就是一族超边的集合。相对图，超图能够模拟更广泛的关系。在最近的几十年里，超图已经受到广泛学者的关注[2-5]。

覆盖是一类常见的数据结构。作为处理这类数据的有效工具，覆盖粗糙集[6]已经受到越来越多学者的广泛关注。比如，在理论上，近似算子模型的提出[7,8]、覆盖公理系统的建立[9,10]、覆盖约简问题的研究[11-12]及其与其它学科的联系[13,14]。在应用上，覆盖粗糙集已被广泛用于属性约简[15]与规则提取[16]等多个领域。

由于超图与覆盖粗糙集均是建立在集合之上，因此本文将这两者进行结合，利用覆盖粗糙集研究超图的连通性问题。首先，文章开头将覆盖近似空间与超图联系起来，有趣的是由不含孤立点的无向简单超图的顶点集与边集组成的有序数组构成一个覆盖近似空间。其次，在此覆盖近似空间上利用覆盖近似算子和次覆盖上近似算子给出了连通超图的几个等价刻画。

本文的段落安排如下：第二节回顾了覆盖粗糙集与超图的一些基本概念；第三节为主要内容，给出了连通超图的几个等价刻画；第四节对本文进行总结并提出下一步研究的方向。

1 预备知识

为了便于讨论，本节回顾有关于覆盖粗糙集及超图的一些基本概念。

1.1 覆盖粗糙集

作为划分的推广，覆盖更具普遍性和试用性。本小节首先介绍覆盖的定义。

在覆盖近似空间中，覆盖上下近似是该空间中的两个核心的概念。

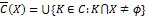
紧接着，下述命题给出了上近似算子的一些性质。对应的关于下近似算子的性质可根据对偶性得到。

1.2 超图

超图是模拟数据之间相关性的一种离散结构。理论上，超图的定义如下：

超图中的边可以是有向的或者无向的。若是所有的边均是无向的，则称此超图为无向超图。在此情况下，对于超图中的任意两个顶点（可相同），如果存在一条超边包含它们，则称这两个顶点是相邻的。孤立点是指那些不与中任意点（包含该点本身）相邻的点，即设,若，则称为的孤立点。

图1 例1中的超图

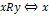
2 主要内容

本节将利用覆盖粗糙集研究超图的连通问题。首先我们建立起超图与覆盖之间的关系。

根据超图的定义，不难将超图的定义与覆盖近似空间联系起来。事实上只需要求超图不含孤立点，那么这两个概念就可互相等价。

由此，若无特殊说明，下文所讨论的是不含孤立点的简单超图的连通性问题。接下来的命题从边集的角度刻画了连通超图的特征。

基于上述命题，我们从超图的边出发给出连通超图的一个等价刻画。

证：根据命题3和连通超图的定义，定理得证。

事实上，根据定理1，我们也可以从覆盖上近似算子的角度刻画连通超图。

根据对偶性，连通超图也可以用覆盖下近似的角度来刻画。

…

证：结合连通分支的定义与命题4，定理得证。

如果一个超图是连通的，那么它只含有一个连通分支，反之亦然。因此根据定理3便可给出连通超图的另一个等价刻画。

图3 例3中的超图

根据上述定理，便可得到以下推论。

3 结束语

本文从覆盖粗糙集的角度讨论了不含孤立点的无向简单超图的连通性。对于这一问题的研究主要从覆盖近似算子和次覆盖上近似算子这两个方面出发。尽管本文对超图的性质进行了研究，但还是有许多值得研究的问题：

(1) 超图的诞生是为了模拟更复杂的系统。当它用于模拟模糊二元或者多元关系的时候，此时的超图就是模糊超图。那么如何用模糊粗糙集来研究模糊超图？

(2) 现实生活中不少问题可被抽象为有向超图，如离散事件系统。在这类系统中连通性起着非常重要的作用。因此有向超图的强连通性也是值得进一步的研究的课题。

[1] BERGE C. Hypergraphs-combinatorics of finite sets[M].North-Holland Mathematical Library, 1989.

[2] Ouali M O, Fohlin H, Srivastav A. An approximation algorithm for the partial vertex cover problem in hypergraphs[J]. Journal of Combinatorial Optimization.2016,31:846-864.

[3] Huang Y, Verbraeck A, Seck M. Graph transformation based simulation model generation[J]. Journal of Simulation.2016,doi:10.1057/jos.2015.21.

[4] Sen M K, Dasgupta U. Hyperrelations and generalized hypergraphs[J]. International Journal of Machine Learning and Cybernetics.2013,4:565-574.

[5] Alon N, Yuster R. On a hypergraph matching problem[J]. Graphs and Combinatorics. 2005, 21: 377-384.

[7] Pomykala J A. Approximation operations in approximation space[J].Bulletin of the Polish Academy of Sciences, Mathematics. 1987, 35: 653-662.

[8] Yao Y, Yao B. Covering based rough set approximations[J]. Information Sciences.2012, 200: 91–107.

[9] Zhang Y L, Li C Q, Lin M L, Lin Y J. Relationshipsbetween generalized rough sets based on covering and reflexive neighborhood system[J]. Information Sciences. 2015, 319: 56-67.

[10] Zhang Y L, Luo M K. On minimization of axiom sets characterizing covering-based approximation operators[J]. Information Sciences. 2011, 181: 3032-3042.

[11] Zhu W. Relationship between generalized rough sets based on binary relation and covering[J]. Information Sciences. 2009, 179: 210-225.

[12] Zhu W. Relationship among basic concepts in covering-based rough sets[J]. Information Sciences. 2009, 179: 2478-2486.

[13] Huang A P, Zhu W. Connectedness of graphs and its application to connected matroids through covering-based rough sets[J]. Soft Computing. 2016, 20(5): 1841-1851.

[14] Huang A P, Zhao H, Zhu W. Nullity-based matroid of rough sets and its application to attribute reduction[J]. Information Sciences. 2014, 263: 153-165.

[15] Min F, Zhu W. Attribute reduction of data with error ranges and test costs[J], Information Sciences. 2012, 211:48-67.

[16] Zhang B W, Min F, Ciucci D, Representative-based classification through covering-based neighborhood rough sets, Applied Intelligence, 2015: 1573-7497.

Connectedness of Hypergraphs ThroughCovering-Based Rough Sets

HUANG Aiping, Huang Fengying

(School of Information Science and Technoalogy, Xiamen University Tan KahKee College, Zhangzhou 363105, China)

As a generalization of graphs, hypergraph are widely used in data data mining. In this field, a data structure is usually designed in the form of hypergraph. In data mining, the data are usually presented in the form of covering and covering-based rough sets provide a systematic approach to this type of representation. In this paper, we study the connectedness of hypergraphs through covering-based rough sets. We present an approach to inducing a covering by a hypergraph and then study the connectedness of the hypergraph from the viewpoint of covering approximation operators. The results show that this paper provides a new approach to studying hypergraphs.

covering-based rough set, hypergraph, hypergraph connectedness

1672-9129(2016)02-0011-04

TP3

A

2016-09-07；

2016-09-27。

国家自然科学基金 61379098。

黄爱萍(1988－)，女，硕士，讲师，主要研究方向：数据挖掘，粗糙集，拟阵 (sxxhap@163.com)；黄凤英(1989－)，女，硕士，讲师，主要研究方向：数据分析，物联网。

(*通讯作者电子邮箱：sxxhap@163.com)