基于时域和频域分析的振动传感器改进方法

佘磊，段国栋



基于时域和频域分析的振动传感器改进方法

佘磊*，段国栋

中国航发成都发动机（集团）有限公司，成都 610503

测振是发动机性能分析的重要组成部分，在航空领域起着关键作用。振动传感器采集并分析振动加速度的时间历程，找出航空发动机振动根源和机械噪声产生的原因。本文提出一种基于时域和频域分析的振动传感器改进方法。首先在不同飞行状态下对发动机进行振动性能测试，获得振动和噪声的时序和频谱。然后利用传递函数、传感器频率响应分析推导出传感器频率响应曲线公式，计算出传感器一阶固有频率和相对阻尼系数。最后根据振动频谱和噪声频谱，提出了一种更加有效的测振方法。在国产某型飞机发动机的实测结果表明，所提出措施能有效提高振动传感器测量准确度。

振动传感器；航空发动机；测振方法改进；时域分析；频域分析.

引言

发动机工作过程中，一般通过加速度或速度传感器来测量振动信号[1]。最常用的振动测量传感器按工作原理可分为压电式、压阻式、电容式、磁电式及光电式[2]。磁电式振动速度传感器（即速度计）由于具有输出信号大、后续电路简单、抗干扰能力强的优点，在低频传感器中得到广泛应用[3]。

本文提出了一种基于时域和频域分析的磁电式振动传感器改进方法。首先在不同飞行状态下对发动机进行振动性能测试，获得振动和噪声的时序和频谱[6]。然后利用传递函数、传感器频率响应分析推导出传感器频率响应曲线公式，计算出传感器一阶固有频率和相对阻尼系数。最后根据振动频谱和噪声频谱，提出了一种更加有效的测振方法。

在国产某型航空发动机通过灵敏性实验、带通实验、发动机随机振动实验验证该性能参数下传感器性能。实测结果表明，所提出改进方法能有效提高振动传感器测量准确度。

1 传感器数学模型

在进行传感器设计的时候需要解决如下几个重要问题[4]：

（1）要求传感器有高的稳定性和可靠性；

（2）要求有宽广的频率范围；

（3）传感器的灵敏度能在一个小的公差范围内；

（4）设计一套能在10-1000HZ范围内正常工作的振动校准机构，以便调试；

（5）要求传感器有较强的抗横振能力。

1.1 微分方程

振动传感器是一种动态传感器，被测物理量为加速度、速度和位移。其输入和输出都是连续时间信号，其数学模型是微分方程，它描述的是传感器输入和输出的关系，输出是否良好的随输入量变化是一种重要指标，这就需要我们研究传感器的动态响应特性。

一般采用线性时不变系统描述传感器动态特性，即用线性常系数微分方程表示输入和输出关系[3]：

（零阶环节） (2)

（二阶环节） (4)

1.2 传递函数

传递函数是以代数式的形式表征了系统本身的传输、转换特性，而与激励及系统的初始状态无关。是描述线性时不变系统的输入输出关系的一种函数，因此本文用它表示系统的动态特性。传递函数数学定义为初始条件为零时，输出量（响应函数）的拉普拉斯变换与输入量（激励函数）的拉普拉斯变换之比。线性系统激励x(t)与响应y（t）满足式3，即：[3]

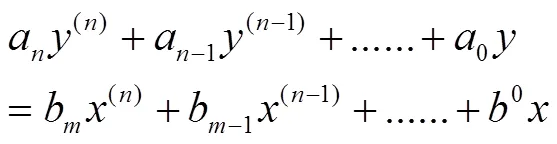
对上式拉普拉斯变换得[3]：

(6)

对于传感器一般m＜n。式中s的幂次代表了系统微分方程的阶数，式9中取，则。为收敛因子，为角频率，，为拉普拉斯自变量，是复数。

7式中：

是输出的拉普拉斯变换[3]；

(9)

是输入的拉普拉斯变换[3]。

1.3 传感器频率响应分析

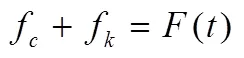
该系统可以写为[3]：

由此速度传感器可以近似看成一阶系统，可以与前式5式相比较，两边除以得：

将其进行拉式变换得[3]：

(13)

其传递函数为[3]：

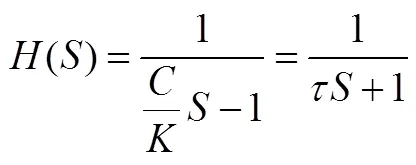
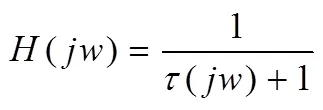
(16)

(17)

2 传感器设计

如下图为传感器的内部结构[4]：

图1 传感器内部结构图

2.1 弹性元件和阻尼系统

为使传感器有较低的工作频率下限和较低的灵敏度下限，必须尽可能降低传感器的自振频率，减少运动系统的摩擦阻力以及选用适当的阻尼，为此振动传感器的运动系统采用三点式轴承架悬挂机构，并用压板将其固定，然后用弹簧支撑，使其在静态时水平方向上一直保持在中线位置，实践证明该悬挂机构不但有较强的支撑性及抗拉能力，而且大大降低运动系统的摩擦阻力，尤其是水平安装状态时使传感器能够敏感小量级运动[5]。

由于速度传感器主要在固有频率上工作，因此确定一阶固有频率很重要，通过计算可以得到不同材料在不同结构参数的一阶固有频率，fo,δz与fo之间有下列关系:

δz弹簧受线圈重力发生变形的阻尼系数，其变形曲线沿弧长展开。实验要求fo在20HZ以下能满足要求。

为使传感器频率响应曲线尽可能向低频扩展，并具有+0，-3dB频率响应曲线，传感器灵敏度S的频率响应曲线公式为[9]：

为传感器灵敏度，为磁感应强度，为线圈平均每匝长度，为线圈匝数，为振动频率与一阶固有频率之比，为相对阻尼系数。

要求传感器的灵敏度频率响应范围保证在35-500HZ≤10%。

可以通过上面两项公式计算fo和，并进行多次对比实验初步选定传感器。

2.2 振动传感器特性需求

振动传感器一个很重要的特性是要有好的抗横向振动能力，即传感器在受到非敏感轴方向振动时，仍能正确的反映敏感轴的振动情况，传感器设计保证传感器受到6g峰值横向加速度情况下仍然能正常工作。

H型传感器要求水平安装灵敏度变化≤10%，经测试实际灵敏度变化在3%范围内。

线圈引出线的一端随线圈高频振动而另一端是固定的，要求引出线即能承受长时间高频振动，焊接点不疲劳断裂，又不妨碍线圈组件和壳体相对运动，我们通过反复摸索，解决了这个问题。

工作温度范围在-40-300℃已满足要求。

通过至少十台次的发动机随机振动实验。

3 振动传感器实验设计与实验分析

3.1 实验环境

振动传感器；二次表头；标准振动台与数字电压表等。温度(20±5)℃，相对湿度≤80%，电源电压变化应在额定电压的±10%范围内，室内无腐蚀性介质，无明显的干扰振源和电磁场。

下图为使用标准振动台对振动传感器进行实验的系统图及使用软件进行测振的界面，传感器就安装在振动台体上：

图2 实验系统图

图3 测试软件界面

3.2 实验内容及步骤

（1）测试振动传感器在室温条件下的电阻值及绝缘性，测量结果为R=898Ω，绝缘：∞。

（2）传感器与二次仪表进行匹配线性度实验：测试范围0~10g(g为一个重力加速度)，测试结果指示准确，结论合格，见下图：

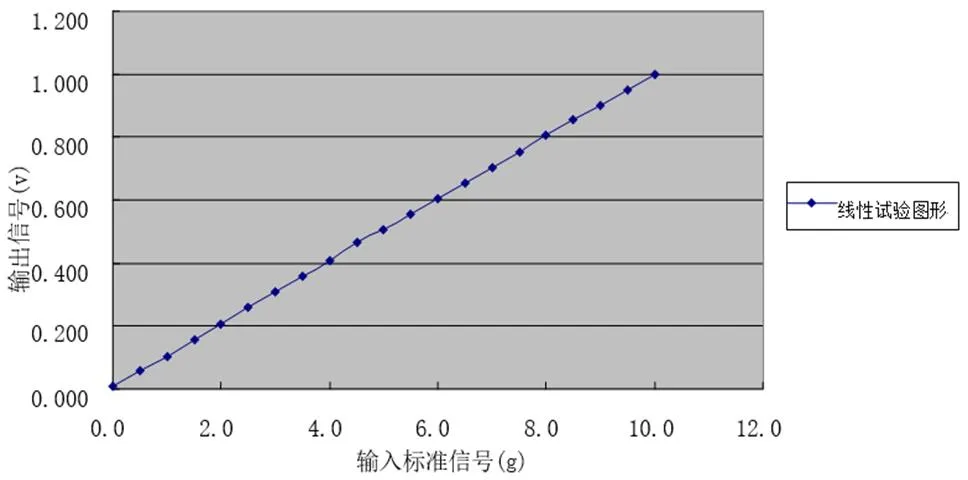
图4 传感器与二次仪表进行匹配线性图

由图示看出振动传感器输出电压的线性拟合曲线，当振动频率为160HZ时，在0-10g范围内该传感器线性良好，结论：合格。

（3）进行传感器灵敏性实验，测试频率：160HZ，测试结果：0.1g开始起振。

（4）升程和回程的测量，此实验反映传感器是否有迟滞（回差滞环）现象：对传感器和二次表头进行0~6g范围内升程和回程的测量，仪器自校7.4。以下为振动传感器与二次表头调校匹配后升程和回程的测量：

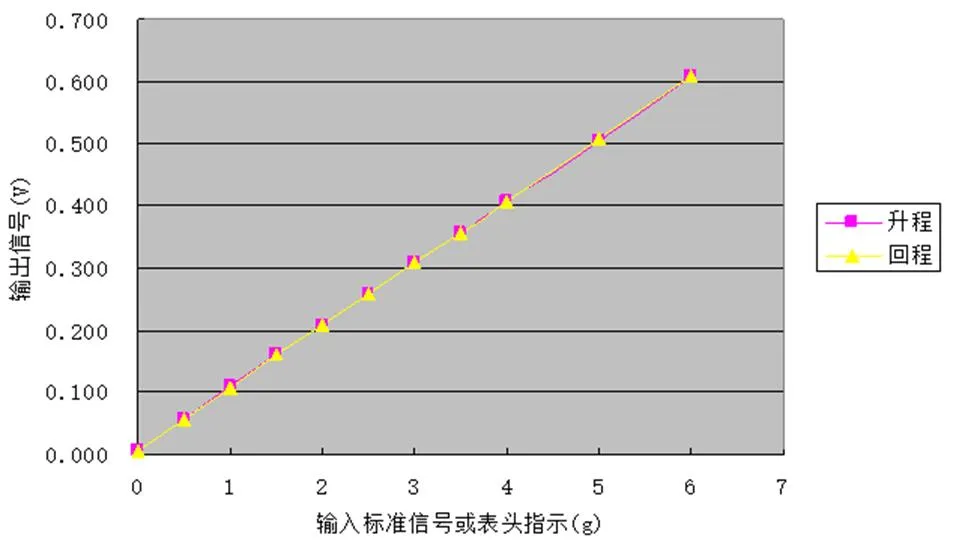
图5 升程与回程线性重合的测量

由图上看出升程和回程完全线性重合，升程和回程测量所得的输出信号伏值基本一致，说明升程和回程传感器没有迟滞（回差滞环）现象。

（5）进行带通实验，在70HZ~200HZ频带范围内，给定标准为3.0g。实验结果：最小2.9g到最大3.2g的实验值主要分布在115HZ~120HZ频率的范围内。计算：20Log 3.2/2.9=0.855dB，要求应不大于1 dB，结论合格。

（6）传感器输出插头接2号和3号插针—电势信号输出端。

（7）对振动传感器进行准确度的测量与计算。在振动频率为160HZ时，振动速度越大输出电压越大。实验生成图形：

图6 振动速度与输出电压线性图

（8）稳定性分析，我们以40mm/s速度为基准在20HZ~300HZ的频率范围内取几个点证实输出电压信号的稳定性：可见在振动速度为40mm/s时，140HZ~250HZ频率的范围内输出电压稳定性好。实验生成见下图：

图7 不同频率下输出电压的稳定性图

注：国家检定规定，用一个点，“160HZ”，传递值采9个点，进行准确度计算，结论不大于10%，为合格。所以我们取频率160HZ，速度40mm/s为基准采集9个点进行准确度计算，以下为部分数据：

5mm/s的偏差：（39.0×2×4－306.5）/306.5×100%=1.79%。

10mm/s的偏差：（77.3×4－306.5）/306.5×100%=0.88%。

20mm/s的偏差：（153.3×2－306.5）/306.5×100%=0.032%。

30mm/s的偏差：（230.3÷3×4－306.5）/306.5×100%=0.18%。

50mm/s的偏差：（382.4÷5×4－306.5）/306.5×100%=-0.189%。

60 mm/s的偏差：（458.4÷6×4－306.5）/306.5×100%=-0.29%。

从以上结论可以看出该传感器性能优于2%，小于国家规定的10%，振动传感器完全满足某型发动机测振要求，能达到测振所需准确度等级。

3 发动机随机振动实验

此传感器已经进行了实验室实验，满足要求，但还需在发动机上进行随机振动实验才能最后下结论。

表1 新旧传感器在不同状态下振动测量

振动传感器进行随机振动实验方案：对发动机在慢车——0.8额定——额定——最大——加力共5个阶段测振并录取稳态时振动值，记录振动参数[7]。发动机需进行两次开车，第一次开车使用原装传感器测振，第二次开车使用新型传感器测振，两次开车程序完全相同。以下为使用原装传感器和新型传感器进行发动机开车实验的对比数据表，我们用“旧”代表原装，用“新”代表新传感器，用E代表发动机额定状态：

对表中数据进行图像对比，如表1所示：

图8 新旧传感器在不同状态下振动测量

如上图可以看出两条线在相同状态下测振数值相差不超过±0.5g。

4 结语

经过时域和频域分析，本文提出的振动传感器改进方法能有效提高测振准确度。在相同的状态下原装振动传感器和新型振动传感器测振数值相差最大为±0.3g。实验要求在相同状态下传感器最大误差不大于±0.5g，可见此振动传感器满足实验要求准确度等级，可以投产使用。

[1] 王俨剀, 王理, 廖明夫. 航空发动机整机测振中的基本问题分析[J]. 航空发动机. 2012(03): 49-53.

[2] 李翠, 李效民, 钟美芳. 压电式加速度传感器的智能应用[J]. 实验室研究与探索. 2010(10): 231-234.

[3] 徐锡林. 磁电式低频振动传感器[J]. 上海机械. 1980(11): 19-25.

[4] 刘洁. 基于磁电式速度传感器的振动测量系统[J]. 机电产品开发与创新. 2010(06): 135-137.

[5] 刘敏. 磁电式速度传感器的使用和运行分析[J]. 浙江电力. 2011(02): 50-52.

[6] 苏尚美, 冯国全, 胡春艳, 徐纲. 某型航空燃气轮机整机振动分析[J]. 燃气轮机技术. 2014(02): 29-33.

[7] 杨玲, 王克明, 张琼. 某型航空发动机整机振动分析[J]. 沈阳航空工业学院学报. 2008(05): 9-15.

[8] 杨忠根, 任蕾, 陈红亮. 系统状态变量分析和系统时域分析的关系[J]. 电气电子教学学报. 2010(04): 9-12.

[9] 王喆, 刘戬, 王飞宇, 刘剑峰. 基于重采样的差分频域分析方法[J]. 计算机学报. 2015(04): 783-792.

Aero-Engine Vibration Transducer Improvement through Time-Domain and Frequency-Domain Analysis

SHE Lei*, DUAN Guodong

（AECC Chengdu Engine (Group) CO., LTD., Chengdu, 610503）

Vibration measurement is an important part of aero-engine performance analysis. Vibration transducer can find the reason of aero-engine vibration and mechanical noise through collecting and analyzing the time series of vibration acceleration. In this paper, we propose an improved method of vibration transducer based on time-domain and frequency-domain analysis. First, we obtain the time series and frequency spectrum through vibration performance test under different regime of flight. Second, we employ the transfer function to derive a sensor frequency response curve formula and compute first order natural frequency and relative damping coefficient. Finally, we propose a more efficient method of vibration transducer based on vibration frequency and noise frequency. Experimental result based on domestic certain type aircraft engine shows that our method can effectively improve the accuracy of vibration transducer measurement.

vibration transducer; aircraft engine; vibration measurement improvement; time-domain analysis; frequency-domain analysis.

1672-9129(2016)02-0031-05

V414

文标献志码: A

2016-09-10；

2016-09-24。

国家自然科学基金青年基金（No.61503312）。

佘磊(1980-)，女，甘肃兰州，工程师，本科，主要研究方向：航空发动机试车台架地面设备、发动机实验设备。

(*通信作者电子邮箱：shirlysl@163.com)