基于拓扑邻域的序信息系统属性权重确定方法

李敬，张盼盼，王利东



基于拓扑邻域的序信息系统属性权重确定方法

李敬，张盼盼，王利东*

(大连海事大学数学系, 辽宁大连市邮编：116026)

在多属性决策中，属性权重是影响决策结果的重要因素，其可由决策群体根据偏好信息直接给出、也可根据数据分布差异性来确定。然而，属性之间的关联性往往被忽视，准确地刻画多个属性之间的相互关系，有利于获得较为客观的决策结果。针对序信息系统属性权重问题，本文基于AFS拓扑邻域构建属性模糊测度度量方法及相应的Choquet积分，并将其应用于学生成绩排名问题中。实例分析表明所构建方法能有效地利用多粒度信息来减少属性确定中的主观程度和体现属性间的关联度。

序信息系统; 拓扑邻域；属性权重; Choquet 积分; AFS代数

引言

多属性决策问题主要解决多个属性下的方案排序问题，其在工程、经济、管理、军事等领域有着广泛的应用，是决策科学领域一个很重要的研究方向。属性权重一般由决策者根据偏好信息直接给出。但是，由于客观事物的复杂性和不确定性以及人类思维的模糊性，人们往往不能明确地给出属性的权重信息。因此，对于这类问题的深入研究有着重要的理论意义和实际应用背景。

近年来，关于如何确定属性权重的多属性决策问题已经引起了国内外学者的关注。岳立柱与闫艳[1]提出了一种无需决策者构造判断矩阵确定属性权重的方法。Pedrycz 和Song[2]建立了基于群AHP的属性权重的确定方法。Zheng等[3]提出基于ELECTRE TRI 模型的属性权重方法。这些方法都假设各个属性是相互独立的。但是在实际生活中，决策问题的各个属性往往具有某种相互作用或者说相关性，这是现实中普遍存在的一类多属性决策问题。粗糙集是一种度量信息系统或决策信息系统中属性评价的有力工具，其通过正域不变、规则不变、分布规律不变和风险代价最小等原则对各类信息表中的属性进行约简、选择。陈娟和王国胤等[4]在不协调序信息系统中给出基于属性重要性的正域约简算法。王虹和石慧娟将分配约简方法扩展到区间型不协调序决策信息系统属性约简中[5]。曹秀英与梁静国[6]根据粗糙集理论中属性重要度的判断方法，提出将主观权重同粗集理论确定的属性重要度相结合确定属性权重。文献[7]将三支决策引入属性评价中，并建立了一种属性评价的三支决策方法。

Choquet积分是一种刻画属性相关性的有效测度方法，它以较弱的单调性和连续性来代替可加性，能够对属性的重要程度进行刻画，因而能够使决策结果更加客观[8]。Choquet积分已经应用到多种形式背景的决策问题中。许永平等人[9]提出了一种考虑属性间的关联作用对于属性权重的影响的TOPSIS语言群决策方法。梁霞等人[10]针对属性具有关联关系的多属性决策问题，提出一种新的C-TODIM 决策方法。刘荣弟等人[11]建立了基于属性关联的R-Topsis决策模型。Wang 和Liang等[12]学者建立一种基于客观信息的粒计算方法，其利用序信息系统中属性值的偏序关系建立偏序粒，再定义偏序粒之间的相似度进而得出属性的测度值，进而结合Choquet积分对方案进行排名。

由于序信息系统广泛存在于生产和生活问题中，其上的属性重要性衡量、属性约简、规则提取受到广泛关注[13,14,15,16,17,18]。目前，在粗糙集等领域，扩展形式多粒度的优势关系及复杂的邻域系统已经开始受到学者的关注，例如文献[19]建立了多粒度优势类决策方法。本文从一个属性集与其子集所有可能生成的多粒化邻域的相对变化率来刻画属性的重要性。受文献[12，20]启发，在基于拓扑邻域等相关研究基础上, 针对序信息系统建立基于拓扑邻域属性模糊测度方法，充分利用属性集可能生成的多粒化邻域信息，同时可以减少属性确定中的主观程度。

1 基础知识

本节介绍本文中所用到的模糊测度、一种AFS代数和拓扑邻域。

1.1 模糊测度和Choquet 积分

模糊测度用单调性代替了传统测度的可加性，扩展传统测度应用范围，并可用于权重的确定[8]。其定义如下：

定义1[21]：在集合上的函数是模糊测度，如果它满足以下公理：

定义2[22]：是定义在集合上的模糊测度，的元素记作。函数关于模糊测度的离散Choquet积分定义为：

1.2 AFS代数

AFS方法优点是可生成便于理解的语义描述，其语义描述是利用“and”和“or”生成的描述逻辑。首先引入符号和代数，表示属性或概念的集合。则有如下定义：

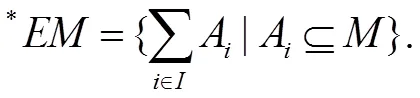
定义3[20]：假设是一非空集合,在上定义如下的二元关系如下：对任意的,

定理1[20]：假设是一非空集合,在上定义如下的二元运算和对任意的,下式成立：

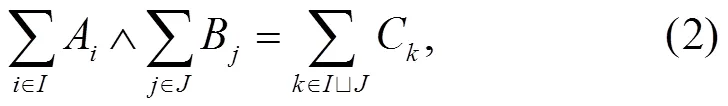
定义4[20]：设是代数。在上定义如下序关系：对任意的,当且仅当对任意的,存在使得成立。

引理1[20]：假设是一非空集合，是上的代数。令,,,对任意的，则有下列结论:

1.3 AFS 拓扑邻域

定义5[20,23]：假设和均是非空集合，是上的代数。是上的拓扑分子格。对任意,, 称为由诱导的的邻域；称为由诱导的的邻域。

由定义6可得以下性质。

2 数值例子

本文选用文献[12]中例子，来获得各个属性的测度值。假设在五个优秀学生中进行奖学金评比，其评比内容包括三个科目，记为，五个学生记为，具体信息见表1。

表1 五个学生的成绩表[12]

利用定义6可以得到：

模糊测度值：

同理可得：

进一步，根据定义2，对各科成绩进行Choquet 积分加权求和：

由此得到最后学生排名情况：

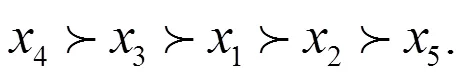
得到的结果与文献[12]的排名一样，但所使用属性测度不同。基于AFS拓扑邻域的属性重要性度量中，考虑的邻域是属性集合在“交”与“并”运算下诱导的多粒度邻域，其包含了单优势粒度生成的邻域[12]。因此本文的属性权重确定方法可以看作是文献[12]中方法的多粒度扩展。

3 结论

针对序信息系统属性权重问题, 本文从粒计算角度出发寻找设计一种由序关系确定属性之间的关联度量方法。本文基于AFS拓扑邻域，定义了由属性变化而引起的邻域数量的相对变化量，进而建立了衡量属性关联度量方法及相应的Choquet积分，并将其应用于学生成绩排名问题中。实例分析表明了所构建方法能有效地利用多粒度邻域信息来减少属性确定中的主观程度及属性间的关联度。

[1] 岳立柱, 闫艳. 基于序数信息的属性权重确定方法[J]. 统计与决策, 2015 (13): 78-80.

[2] Pedrycz W, Song M. Analytic Hierarchy Process (AHP) in Group Decision Making and its Optimization with an Allocation of Information Granularity [J]. IEEE Transactions on Fuzzy Systems, 2011, 19(3), 527-539.

[3] Zheng, Stéphane Aimé Metchebon Takougang, Vincent Mousseau, Marc Pirlot. Learning criteria weights of an optimistic ELECTRE TRI sorting rule [J]. Computers & Operations Research 2014 (49): 28–40.

[4] 陈娟, 王国胤, 胡军. 优势关系下不协调信息系统的正域约简[J]. 计算机科学, 2008, 35(13): 216-218.

[5] 王虹, 石慧娟. 基于优势关系的不协调区间值目标信息系统的分配约简[J]. 模糊系统与数学, 2014, 28(4): 152-158.

[6] 曹秀英, 梁静国. 基于粗集理论的属性权重确定方法[J]. 中国管理科学, 2002, 10(5): 98-100.

[7] 刘盾, 李天瑞, 苗夺谦, 王国胤, 梁吉业. 三支决策与粒计算[M]. 科学出版社, 2013.

[8] Wang Z, Klir G. Fuzzy measure theory[M]. Springer Science & Business Media, 2013.

[9] 许永平, 王文广, 杨峰, 王维平. 考虑属性关联的TOPSIS 语言群决策方法[J]. 湖南大学学报: 自然科学版, 2010, 37(1): 49-53.

[10] 梁霞, 姜艳萍, 梁海明. 考虑属性关联的 C-TODIM 决策方法[J]. 运筹与管理, 2015, 24(2): 101-107.

[11] 刘荣弟, 刘静霞, 李言辰, 等. 考虑属性关联的不确定语言变量R-TOPSIS 模型[J]. 价值工程, 2015, 34(16): 199-201.

[12] Wang B L, Liang J Y, Qian Y H. Preorder Information Based Attributes' Weights Learning in Multi-attribute Decision Making [J]. Fundamenta Informaticae，2014, 132: 331-347.

[13] Zhang Y Q, Yang X B. Intuitionistic fuzzy dominance-based rough set approach: model and attribute reductions [J]. Journal of Software, 2012, 7(3): 551-563.

[14] 邓维斌, 王国胤. 基于优势关系粗糙集的电信客户价值评价方法[J]. 计算机应用研究, 2015, 32(6): 1634-1636.

[15] 刘力凯, 王国胤, 邓维斌. 优势关系粗糙集的移动用户换机预测方法[J]. 小型微型计算机系统, 2015, 36: 1789-1794.

[16] Hu Q H, Guo M Z, Yu D R, Liu J F. Information entropy for ordinal classification [J]. Science in China Series F: Information Sciences, 2010, 53(6): 1188-1200.

[17] 徐伟华, 张文修. 基于优势关系下信息系统分配约简的矩阵算法[J]. 计算机工程, 2007, 33(14): 182-184.

[18] 吴磊, 杨善林, 郭庆. 优势关系下直觉模糊目标信息系统的上近似约简[J]. 模式识别与人工智能, 2014, 27(4): 300-304.

[19] 庄颖, 刘文奇, 范敏, 李金海. 集值信息系统上的多粒度优势关系与信息融合[J]. 模式识别与人工智能, 2015, 28(8): 741-749

[20] Liu X. D, Pedrycz W. Axiomatic Fuzzy Set Theory and Its Applications [M]. Springer Verlag, Berlin, 2009, Studies in Fuzziness and Soft Computing, vol. 244.

[21] Demirel T, Demirel N, Kahraman C: Multi-criteria warehouse location selection using Choquet integral, Expert Systems with Applications, 37, 2010, 3943-3952.

[22] Grabisch M, Sugeno M, Murofushi T. Fuzzy measures and integrals: theory and applications [M]. Springer-Verlag New York, Inc, 2000.

[23] Wang L D, Liu X D, Qiu W R. Nearness approximation space based on axiomatic fuzzy sets [J]. International Journal of Approximate Reasoning , 2012(53): 200–211.

[24] 徐伟华. 序信息系统与粗糙集[M]. 科学出版社, 2013.8.

A Method of Determining Weights Based on Topology Neighbourhood for Ordered Information System

LI Jing, ZHANG Panpan, WANG Lidong

(Department of Mathematics, Dalian Maritime University, Dalian 116026, P.R. China)

Attribute weight plays an important role in influencing the decision results in multiple attribute decision-making. Attribute weight can be given by decision group based on preference information and determined by the differences of data distribution. However, the correlation of attributes is usually ignored. In order to obtain the better decision results, the interrelation of multiple attributes should be reflected accurately. In this paper, a measurement method is established based on AFS topology neighbourhood, which is combined with Choquet integral to form a rank method. What’s more, we apply it to the ranking of students’ mark. The example illustrates that the proposed method can make a good use of multi-granular neighbourhood information to reduce the subjective degree of determining attribute and reflect the degree of association among attributes.

ordered information system; topology neighbourhood; Attribute weight; Choquet integral; AFS algebra

1672-9129(2016)02-0026-05

TP18

A

2016-09-13；

2016-09-27。

国家自然科学基金（61203283）、辽宁省自然科学基金（2014025004，201602064）、中央高校基本科研基金（3132016306，3132016220）。

李敬(1992-)：女，山东济南人，硕士生，研究方向为多属性决策、数据处理与信息提取；张盼盼 (1992-)：女，山东济南人，硕士生，研究方向为模糊数学；王利东(1979-)：男，辽宁喀左人，副教授、硕士生指导教师，研究方向为粒计算、多属性决策。

(*通讯作者电子邮箱：ldwang@hotmail.com)