基于混沌时序方法的油田产量预测研究

高丽洁，檀朝东*，程心平，郑春峰，李欣伦，刘萍



基于混沌时序方法的油田产量预测研究

高丽洁1，檀朝东1*，程心平2，郑春峰2，李欣伦1，刘萍3

(1.中国石油大学（北京），北京昌平，102249； 2.中海油能源发展股份有限公司工程技术分公司，天津塘沽，300450；3.北京雅丹石油技术开发有限公司，北京昌平，102200；)

油田产量的预测一直是石油工业的重要研究课题。由于油田产量影响因素多且复杂，本文采用混沌时序预测方法进行研究。构造油田产量预测的混沌时序分析模型，用C-C方法确定相空间重构参数嵌入维度与延迟时间；使用小数据量法计算最大Lyapunov指数用于判别产量时间序列的混沌性；利用加权一阶局域预测法对油田产量进行预测。最后利用渤中油田某平台某井数据进行产量预测并验证模型的准确性。

混沌时序；相空间重构；C-C方法；产量预测.

引言

油田产量的预测在油田动态分析中一直占有重要的地位，对油田产量预测的研究也从未停止。但是油田的产量变化是一个比较复杂的问题。虽然从总体上讲，油田产量都要经历从上升到平稳再到下降的过程，但是由于油田的自然地质条件不同，开发方式不同，采取的措施不同，多数油田产量呈现非常复杂的变化。同时，一个油田的产量是由各单井的产量叠加而成，而油井也处在投产、作业和停产的不断更替之中，各种驱替液的注入，油水井各种增产增注措施无不改变地下渗流状况及整个油田的产量。所以说油田是一个高度复杂的开放的系统，高度非线性的，既有主导地下复杂介质下渗流的各种线性或非线性确定性方程，又有人为的各种随机因素的作用。国内外常规的产量预测方法主要有神经网络、递减曲线法、翁氏旋回法、组合预测等[7]。但是常规方法已经不再适用于具有高度非线性的复杂油田了，所以需要在常规的方法之外，寻找一种新的油田复杂系统中产量的预测方法，即基于混沌时间序列预测方法。文献[1]以胜利油区孤岛油田某区块产油量为实际数据进行分析，提出以部分复杂油田产量序列为混沌时序的方法。但具体问题还需具体分析，所以本文仍需对油田时间序列进行判别然后再预测。

混沌是广泛存在着的一种非周期性运动的形式，具有内在随机性的表现。时间序列分析就是根据事物发展的过去、现在的序列数据，挖掘系统的内在特性和规律，并建立尽可能准确的数学模型。混沌时序分析则为解决具有与随机噪声相似的混乱无序特征的时间序列的有力工具。

1 油田产量预测混沌时间序列分析模型建立

混沌时序分析包括对各种时间序列进行混沌判别及预测控制。混沌系统会表现出“貌似无规则的、类似随机”的现象，但未必所有系统都适用于混沌时序分析方法进行研究，如果不加以判断，盲目套用混沌方法，将得到不准确甚至错误的结论，结果也无法令人信服。混沌现象的出现是有条件的，所以任何非线性系统进行混沌时序分析前需进行判别。混沌时间序列分析的基础是相空间重构理论，因为混沌系统性质参数的计算、判别及预测模型的建立等都必须在相空间进行[1]。相空间重构的质量直接影响到后续分析的效果。混沌时序分析首先用C-C算法计算该样本的延迟时间和嵌入维数，以延迟时间和嵌入维数参数组合进行相空间重构，运用小数据量法计算出序列的最大Lyapunov指数，Lyapunov指数值大于0说明该系统存在混沌特性，然后运用加权一阶局域预测法进行混沌时序预测。

1.1 相空间重构

相空间重构的目的：在高维相空间中恢复出体现混沌系统规律性的混沌吸引子，从而获取更多的隐藏信息。相是指某一系统在一个特定时间的状态，以该系统的可能状态所组成的集合被称作相空间。引起非线性混沌的过程基本上是多变量的，通常时间序列并不能记录某个系统的所有方面，而仅仅是其中的一部分，一般只能得到一维的标量时序，因此需要重构系统的相空间。通过相空间的重构，在无须已知原油生产动态系统数学模型的情况下，可以获得系统的多变量状态表示，使非线性动力学分析方法能用于实验数据的分析和处理，普遍采用坐标延迟重构法[2]。

在原油生产动态系统中，设最主要的观测量——产油量时间序列为{xn}，n=1，2，…，N，N为序列总长度。以延迟时间τ和嵌入维数m进行相空间重构得：

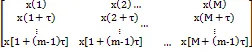
相空间中的相点可以表示为：

X(n)=[x(n)，x(n+t)，…x(n+(m-1)t)]；n=1，2，…，M

M=N-(m-1)t

如果参数延迟时间和嵌入维数选择恰当，则X(n)可描述原系统。由x(n)构造X(n)称为相空间重构。在具体实施相空间重构过程中，如何正确确定延迟时间和嵌入维数是相空间重构成功的关键。本文利用文献[5]提出的C-C算法同时确定延迟时间和嵌入维数。

1.1.1 延迟时间与嵌入维度的确定

1999年，Kim、Eykholt和Salas提出C-C算法[3]，利用关联积分同时计算出最优延迟时间t和嵌入窗宽w，并利用公式tw=(m-1)*t计算出嵌入维数。

将原始产油量时间序列{xn}，n=1，2，…，N分成t 个不相交的时间子序列，长度l=[N/t]（[∙]表示取整）：

{ x(1),x(t+1),x(2t+1),…}

{ x(2),x(t+2),x(2t+2),…}

⋮

{ x(t),x(t+t),x(2t+t),… }

分别计算每个子序列的统计量S(m，N，r，t)：

S(m，N，r，)=

式中Cl是第l个子序列的关联积分，表征相空间中任意两点间距离小于邻域半径的概率，定义如下：

C(m，N，r，)=

r为邻域半径，M=N-(m-1)t为相空间中相点数目，N 是时间序列总长度），q(∙)为 Heaviside 单位函数（定义为，q(x)=0，if x< 0；q(x)=1，if x≥0）。

当N→∞时，记：

S(m, r,)=

根据BDS统计结论，如果时间序列是独立同分布，则N→∞时S(m，r，t)恒为0。S(m，r，t)~t反映了时间序列的自相关特性，当其第一次过零点，或对所有半径 r 相互差别最小时，表示重构相空间中的点几乎是均匀分布，重构吸引子轨道在相空间完全展开。

定义：

∆S(m，t)度量S(m，r，t)~t的第一个零点或∆S(m，t)~t的第一个极小点。

应用BDS统计可得到N，m，r的合理估计，取N=3000，m=2，3，4，5，r=k∙σ/2，k=1，2，3，4，σ是时间序列的均方差。得到方程如下：

现有的C-C算法认为S ̅(t)的第一个零点或∆S ̅(t)的第一个极小点就是最优延迟时间t，Scor(t)的全局最小点就是嵌入窗宽tw[5]。由tw=(m-1)*t即可得到嵌入维数m的值。

根据上述理论建立模型，在MATLAB上编写程序，以要分析的油田实际产量数据为对象，求取延迟时间和嵌入宽度。

图1 C-C算法重构油田产量系统x分量

1.2 混沌系统判别

混沌运动具有初值敏感性，从两个相邻初始点出发的邻近轨道之间的距离将随时间呈指数式分离，这种相空间中相体积收缩和膨胀的几何特性可用Lyapunov指数定量地描述。1983年，格里波基证明只要最大Lyapunov指数大于0，系统就具有混沌性[6]。这成为了混沌判别的主要量化方法之一。本文运用文献[4]中的适合小样本集的小数据量法计算最大Lyapunov指数。

方法原理如下：

在重构相空间后，寻找产量时间序列中每个相点的最近邻近点，例如相点Xj的最近邻点为X(h(j))，记最小距离为：

则最大Lyapunov指数λL可以通过每个相点与其最近邻近点在轨道上的平均发散速率估计出来，即：

其中∆t是所用时间序列的样本周期。

根据Lyapunov指数的定义：

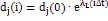
两边取对数有：

若该时间序列的最大Laypunov指数λL>0，则表明该时间序列演化轨迹是发散的，序列具有混沌特征，因而不能够进行长期预报，但可以预知它的最大预报时间尺度Tf，它与最大Laypunov指数有如下的关系，即

Tf=1/λL

这里Tf与∆t的单位相同。

根据上述原理在MATLAB中编程实现小数据量法求取最大Lyapunov指数。以要分析的油田实际产量数据为对象。延迟时间取8，嵌入维度取7，结果如图2所示：

通过最小二乘法对线性较好的一段进行拟合，并求斜率，得到最大Lyapunov指数为：0.0062，这一结果证明了该实际油田产量时间序列确实具有混沌性质。并可进行161天的产量预测。

图2 小数据量法求最大Lyapunov指数

1.3 混沌时间序列预测

混沌时间序列由于内在的非线性动力学特性，不可长期预测，但确定性结构又使系统演化轨迹短期内发散较小，满足短期可预测性。混沌时序预测就是在重构后的相空间中找到某种模型去最大程度地逼近系统的动力学特性，并用这个模型实现系统未来趋势的预测。本文运用加权一阶局域预测法预测油田产量[2]。

一般的局域预测算法中，在找到中心点邻域后，便将邻域中的几个点进行拟合，并不考虑邻域中各点与中心点的空间距离对其的影响。但是，相空间中各点与中心点的空间距离是一个非常重要的参数，预测的准确性往往取决于与中心点的空间距离最近的那几个点，因此，将中心点的空间距离作为一个拟合参数引入预测过程，在一定程度上可以提高精度，并有一定的消噪能力。其基本原理如下：

式中：a为参数，一般取a=1。

加权一阶局域预测法是用一阶线性拟合的方式来逼近相点的演化趋势：

将每个相点分解为各维分量，则有：

使用加权最小二乘法来求取最佳的a和b两个参数值，则问题转化为：

可以初步分为专业岗位(通讯、云计算、软件、财务等)、管理岗位(营销、行政、客服等)、公务岗位(教师、公务员、军官等)、私有岗位(创业者、自由职业等)四级，按照不同的岗位层级进行分类培养。

将上式看成是关于a和b的一元函数，为了求最小值，分别求对a和对b的偏导数：

可求得a和b，从而得到相点演化的预测公式，得到下一步演化相点的预测，提取最后一维分量即为时间序列的预测值。

2 应用于实际油田产量预测

应用以上所建立的混沌时序预测模型对渤中油田某平台某井2006年1月3日到2010年12月29日的日产油量数据进行分析，共421条数据，产量时间序列变化特征如图3所示。

图3 原始产量数据变化曲线

首先根据C-C算法计算系统的延迟时间为t=8嵌入维度为m=7，利用加权一阶局域预测法进行预测，在MATLAB上编程演示，用最后20个样本对预测模型进行了验证，产生结果的平均误差为4.14%，产量时间序列预测值与实际值对比如图4。

图4 实际与预测产量对比图

可以看出，产量预测曲线能够很好地吻合实际值曲线的变化趋势，两条曲线基本重合，但个别点的预测值与实际值差别较大。平均误差不能更好的体现模型预测的准确率，所以为了更客观地评价产量混沌时间序列预测模型的优劣，本文采用性能指标均方误差对模型进行评价。经过计算得出油田产量预测混沌时间序列分析模型的均方误差为0.01629。

根据实例计算结果以及误差分析可以看出，基于渤中油田某平台某井数据进行的产量预测，其预测准确性达到96%，产量时间序列的混沌预测达到了较高的精度，能够运用于实际油田的产量预测中。

图5 相对误差曲线

3 结论

(1) 本文建立了油田产量预测的混沌时序分析模型，并以渤中油田某平台某井2006年-2010年的实际日产油量数据进行了分析，利用MATLAB编程和计算，得到最大Laypunov指数为0.0062>0，确实存在混沌特性。

(2) 利用已建立的模型对渤中油田某平台某油井产量进行了预测，得到较好预测结果，证实混沌时序分析法的确可用于油田产量的预测。同时，虽然整体误差比较小，但仍存在个别误差较大点，所以算法仍需改进。

(3) 同样必须指出对于油田产量序列预测问题，必须具体问题具体分析，有部分油田可能由于开发规律性较强，并不存在混沌现象，所以应用混沌时序分析前务必观察和判别原始序列是否为混沌状态。

[1] 范海军,张丽丽. 复杂油田产量序列的相空间重构及混沌特征分析[J]. 大庆石油地质与开发,2005,02:43-45+106.

[2] 高俊杰. 混沌时间序列预测研究及应用[D].上海交通大学,2013.

[3] KimHSEykholtR, SalasJ. Nonlineardynamics, delay times, and embedding windows [J]. Physica D: Nonlinear Phenomena, 1999, 127(1-2): 48-60.

[4] 陈益峰,吕金虎,周创兵. 基于Lyapunov指数改进算法的边坡位移预测[J]. 岩石力学与工程学报,2001,05:671-675..

[5] 胡瑜,陈涛. 基于C-C算法的混沌吸引子的相空间重构技术[J]. 电子测量与仪器学报,2012,05:425-430.

[6] 修妍. 混沌时序分析中的若干问题及其应用研究[D].天津大学,2007.

[7] 钟仪华,林旭旭,刘雨鑫. 基于多元混沌时间序列的油田产量预测模型[J]. 数学的实践与认识,2016,06:99-105.

[8] 杨永锋,仵敏娟,高喆,吴亚锋,任兴民. 小数据量法计算最大Lyapunov指数的参数选择[J]. 振动.测试与诊断, 2012,03:371-374.

[9] 张海龙,闵富红,王恩荣. 关于Lyapunov指数计算方法的比较[J]. 南京师范大学学报(工程技术版),2012,01:5-9.

[10] 李国辉,徐得名,周世平. 时间序列最大Lyapunov指数的计算[J]. 应用科学学报,2003,02:127-131.

Oilfield Output Forecast Based on the Chaotic Sequence Time Forecasting Method

GAO Lijie1, TAN Chaodong1*, CHENG Xi，nping2, ZHENG Chunfeng2, LI Xinlun1, LIU Ping3

(1.College of Petroleum Engineering, China University of Petroleum (Beijing), Beijing Changping 102249, China; 2.CNOOC Energy Technology & Services- Engineering Technology Co,Tianjin Tanggu 300450;3.Beijing Yandan Petroleum Technology Development Co, Ltd, Beijing Changping 102200)

Oilfield output forecasting is an important research topic for the industry. The factors that impact the oil production are numerous and complex. In this paper, we propose a chaotic sequence time forecasting method. First, the chaotic sequence time analysis model is constructed. The embedding dimension and delay time of phase space reconstruction parameters are determined with C-C method. Second , the Small Datais used to calculate the maximum Lyapunov exponent for judging chaotic characteristics of sequence time. Third, the weighted first order local prediction methodis used to predict oil production. Finally, the data of Bohai oilfield platform are used to predict production and verify the accuracy of the model.

Chaotic time series; phase space reconstruction; C-C method; production forecast.

1672-9129(2016)02-0047-05

TP3

A

2016-09-15；

2016-09-27。

高丽洁(1993-)，女，辽宁宽甸，学生，硕士研究生，主要研究方向：数据挖掘、油井措施诊断；檀朝东(1968-)，男，安徽，副研究员，博士，采油工程，智能油田：程心平（1968 -），男，高级工程师，采油工艺和井下工具。

(*通信作者电子邮箱 tantcd@126.com)