关系粗糙集的邻域拟阵结构研究

刘艳芳，陈雪云



关系粗糙集的邻域拟阵结构研究

刘艳芳*，陈雪云

(龙岩学院信息工程学院，福建省龙岩市 364000)

本文在论域任一关系中，通过邻域定义了一个集族，证明其满足拟阵的独立集公理，建立了邻域拟阵。为了进一步了解邻域拟阵，研究了其极小圈、秩函数和闭包算子。同时，给出了从拟阵诱导关系的一种形式，研究了关系的上近似算子和由其诱导的拟阵闭包算子之间的关系。更进一步的研究了从关系到拟阵再到新关系与原关系之间的关联，尤其是，原关系通过邻域可以等价表示新关系。

粒计算；关系粗糙集；上近似；邻域；拟阵

引言

人类在认识客观世界时，根据对象的不可分辨性，或相似性，或功能性等特性将对象分成不同的子集，即粒，把那些具有相应尺度的信息粒作为一个整体而不是个体来处理，根据问题求解的实际需要，舍弃与当前问题无关的信息细节，从而简化问题的求解。由于认知能力有限，人类往往采用近似的方式而不是精确的方式用已知的概念去刻画另一类事物。粗糙集理论[6]作为当前信息处理研究领域中模拟人类思维和解决复杂问题的粒计算[9]的三大分支之一，它的核心概念是基于等价关系的粒化和基于上、下近似的逼近。因此，粗糙集理论已经在人工智能、机器学习、数据挖掘等领域获得了广泛的应用。

由于等价关系的要求比较严格，很大程度地限制了经典粗糙集的应用领域[3]，1983年Zakowski用一个自反、对称的二元关系替代了等价关系，建立了基于相似关系上的广义粗糙集模型[10]；Urszula给出了基于不同二元关系上的关系粗糙集模型[7]。粗糙集体现了论域中对象间的不可区分性，不包含处理不精确或不确定的原始数据的机制，因此，单纯地使用这个理论不一定都能有效地描述实际问题，需要与理论相互补充[8]，比如模糊集、概率论、证据理论、神经网络和概念格理论等。

作为线性代数和图论的数学理论的一种推广，拟阵论[2]由Whitney在1935年提出的，并且组合优化、算法设计、信息编码和密码学等领域都有着广泛且成功的应用。拟阵理论有着完备的公理体系，和其他理论相结合的研究也受到了很多学者的关注并取得了一定的成果。张少谱等[11]建立了基于自反、传递关系的粗糙集的拟阵结构，并用拟阵的方法为属性约简设计了一个算法；刘艳芳等[4]提出了基于序、传递关系的粗糙集的拟阵结构；为了更好的利用粗糙集与拟阵结合的理论成果；祝峰等[12]提出了粗糙拟阵，把粗糙集与拟阵融合成一体；Marek和Skowron[5]指出将粗糙集的各种推理与拟阵Greedy算法联系在一起，便于开发的算法寻找各类属性集中的最大约简和最小约简，从而促进粗糙集理论中的属性约简算法的进一步发展。

在论域上的任意关系上，本文通过邻域概念给出了一个集族，证明其满足拟阵的独立集公理，进而建立了基于任意关系粗糙集上的邻域拟阵。同时，研究了关系粗糙集的上近似算子和其邻域拟阵的闭包算子之间的关系。更进一步，本文给出了由关系诱导出拟阵的构造方法，在此基础上，研究了由一个关系诱导出一个拟阵，再由这个拟阵诱导出一个新的关系与原来的关系之间的关联。

1 预备知识

本节主要介绍关系粗糙集和拟阵，并给出了一些基本的概念和性质。

1.1 关系粗糙集

粗糙集理论是通过基于关系邻域概念上的一对精确集合：上近似和下近似，来对不确定的目标集合进行确定的近似描述。

粗糙集理论是通过基于关系邻域概念上的一对精确集合：上近似和下近似，来对不确定的目标集合进行确定的近似描述。

定义 1[1]设是论域上任一关系。对任意的，如果，我们说和具有关系，记作。对任意，称集合为关于的邻域，并记为S()。

定义 2[13]设是论域上的任一关系，。我们定义子集关于的下近似和上近似分别为：

（1）

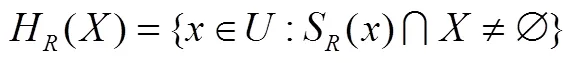
在不引起混乱时，可将L()和H()分别简记为()和()。

由于关系粗糙集中上、下近似算子满足对偶性，所以下面只给出上近似算子满足的性质。

命题 1[13]设是上的任一关系，。H满足以下性质：

(1)； （3）

(2)； （4）

(3)（5）

1.2 拟阵

作为一种同时推广了图和矩阵的概念，拟阵具有完备的公理系统，有许多不同但是等价的定义方法。下面从独立集的角度定义拟阵，在此基础上进一步介绍拟阵的相关集、极小圈、秩函数、闭包算子和闭集等概念和性质。如果没有特别指出，相关内容可参考文献[2]。

定义 3设I是上的子集族。称(, I)为一拟阵，常记为= (, I)，如果I满足如下三个条件：

(I3) 若1,2I且|1| < |2|，则存在2－1使得1{}I。

子集族I中的元素称为拟阵的独立集。因此公理(I1)、(I2)和(I3)称为拟阵的独立集公理。

为了方便地理解拟阵的概念，给出下面不太常用的集合论的运算记号。

定义 4 设A是上的一个子集族。定义：

(A) = {: 对任意A，若，则=（6）

(A) = {:A}。 （7）

定义 5 设= (, I)是个拟阵，。如果I，则称为的一个相关集，记D()为的全体相关集的集合，则D() =(I)。

定义 6 极小的相关集叫做极小圈，记C()为拟阵的全体极小圈的集合，则有C() =((I))。

作为拟阵的一个量化工具，秩函数是一个重要的概念。

定义 7 设= (, I)是个拟阵。称r为拟阵的秩函数，其中

r() ={||:,I}。 （8）

定义8设= (, I)是个拟阵，。在中的闭包为

cl() = {:r({}) =r()}。 （9）

若子集满足=cl()，则称为的闭集。

拟阵和闭包算子是一一对应的，因此，可以从闭包算子的角度来进行定义拟阵。

命题 2 设:()()是个算子。则存在一个拟阵使得=cl当且仅当满足下列性质：

2 邻域拟阵的性质

本节提出了关系粗糙集的邻域拟阵，并研究了其极小圈、秩函数和闭包的表达形式。首先，给出了基于邻域上的一个集族。

定义 9 设是上的任一关系。定义基于下的一个集族如下：

I() = {:,S()S() （10）

事实上，为论域上任意关系，I()满足拟阵的独立集公理。

命题 3 设是上的一个关系。那么I()满足定义3中的(I1)、(I2)和(I3)。

假设1I()，由式（10）可知，存在1使得S() =S()。由1，则有使得S() =S()，这和已知条件I()相互矛盾。因此，必有1I()。

(I3)：如果1,2I()，且|1| < |2|，则存在元素使得1{}I()。

因为1,2I()，由式（10）可知，则对于任意的1,11,11且2,22,22, 都有S(1)S(1)且S(2)S(2)。假设对任意的2－1，都有1{}I()，则存在唯一的一个元素1－2使得S() =S()。因此，有|2－1||1－2|，即|2||1|，这和已知条件|1| < |2|相互矛盾。因此，假设不成立，所以存在一个元素2－1使得1{}I()。

由上面命题可知，对论域上任一关系，I()能诱导出一个拟阵。

定义 10设是上的任一关系。以I()为独立集集族的拟阵称为邻域拟阵，记为()(,I())。

为了能客观了解邻域拟阵的结构，下面给出了一具体的例子。

例 1设= {,,}，且= {(,), (,), (,), (,), (,), (,)}是上的关系。因为S() = {,},S() = {,},S() = {,}。由式（10）可知，邻域拟阵()(,I())的独立集集族I() = {, {}, {}, {}, {,}, {,}}。

在下面的命题，我们给出了邻域与其诱导出的邻域拟阵的相关集之间的关联。

命题 4设是上的任一关系，且()(,I())是由诱导的邻域拟阵。则有

D(()) = {:,, 满足S() =S()}。（11）

极小的相关集就是拟阵的极小圈。根据上面的命题，很容易得到邻域拟阵极小圈的表达式。

命题 5设是上的任一关系，且()(,I())是由诱导的邻域拟阵。则有

C(()) = {{,}:,S() =S()}。 （12）

由上面的命题可知，论域上任一关系诱导出的邻域拟阵的每个极小圈的基数都是2。秩函数是拟阵中的一个量化工具。下面从量化的角度研究邻域拟阵的秩函数。

命题 6设是上的任一关系，且()(,I())是由诱导的邻域拟阵。对，有

r(R)() = |{S() :}|。 （13）

证明由式（8），r(R)() ={||:,I()}。假设r(R)() = |I|，其中I且II()。由式（10），可知I() = {:,S()S()}。因此，有|I| = |{S():I}|。因此，只需证明{S():I} = {S():}。

在秩函数的基础上，提出了拟阵中的闭包算子。下面从邻域的角度研究邻域拟阵的闭包算子。

命题 7设是上的一个关系，且()(,I())是由诱导的邻域拟阵。对，有

cl(R)() = {:，满足S() =S()}。（14）

由上面的众多命题可知，由任一关系诱导出的邻域拟阵的特性均可由其关系等价刻画。那么作为粗糙集中的两个核心概念，上近似和下近似与关系粗糙集的邻域拟阵有什么样的关系呢？下面给出一具体的例子。

表 1 上近似和下近似与关系粗糙集的邻域拟阵

例 2 设= {,,}，且= {(,), (,), (,), (,), (,)}是上的关系。由定义1可得，S() = {,},S() = {,},S() = {}。由式（10），可知邻域拟阵()(,I())的独立集集族为I() = {, {}, {}, {}, {,}, {,}}。根据式（2）和式（8），得到邻域拟阵的闭包和关系粗糙集的上近似如表1。则当= {}，有cl(R)()H()，H()cl(R)()。

当关系是自反关系时，由这个关系诱导出的邻域拟阵的闭包算子包含在基于这个自反关系的上近似算子内。

命题 8 设是上的任一关系，且()(,I())是由诱导的邻域拟阵，。当是自反的，则有cl(R)()H()。

证明由式（14）可知，cl(R)() = {:, 满足S() =S()}，则对于任意的cl(R)()，存在一个元素使得S() =S()。由于是自反的，可得S()，则S()。根据式（2）知H() = {:S()}，因此，H()。

如果关系粗糙集的上近似包含由这个关系粗糙集诱导出的邻域拟阵的闭包，那么这个关系一定是自反关系吗？为了解决这个问题，引入下面的命题。

命题 9[13]设是上的任一关系，。是自反的当且仅当H()。

命题 10设是上的任一关系，且()(,I())是由诱导的邻域拟阵，且。如果cl(R)()H()，那么是自反的。

推论 1设是上的任一关系，且()(,I())是由诱导的邻域拟阵，且。cl(R)()H()的充分必要条件是是自反的。

3 邻域拟阵与拟阵的粗糙集的关系

为了深一层研究关系粗糙集的邻域拟阵，本节引用了一种逆序构造：从拟阵诱导出一个关系。

定义 11[2]设(, I)是一个拟阵。定义上的一个关系()如下：对任意的,，

()=或{,}C()。 （15）

我们称()是由拟阵诱导的关系。

事实上，()是论域上的一个等价关系。

命题 11[2]设(, I)是一个拟阵，()是拟阵诱导出的关系。则()是上的等价关系。

例 3 设= (, I)是个拟阵，其中= {,,}，I = {, {}, {}}。因为C() = {{,}, {}}，因此由式（15），可得() = {(,), (,), (,), (,), (,)}，因此，()是上的一个等价关系。

拟阵的闭包算子和由拟阵诱导出的粗糙集的上近似算子是什么关系呢？为解决这个问题，我们引入下面的命题。

命题 12[2]设= (, I)是个拟阵，C()是的极小圈集族，cl是的闭包算子。则

cl()={:C()，满足{}}。（16）

命题 13 设(, I)是一个拟阵，()是拟阵的诱导的关系。对任意的，都有H(M)()cl()。

但一个拟阵诱导出的关系粗糙集的上近似不包含该拟阵的闭包。下面给出一具体的反例。

例 4 (继续例3) 令= {}。由式（16），可得cl() = {,,}。根据式（2），可得H(M)() = {,}。因此，cl()H(M)()。

由一个拟阵诱导出的关系粗糙集的上近似和该拟阵的闭包在什么条件下相等呢？

定理 1 设(, I)是一个拟阵，()是拟阵的诱导的关系粗糙集。对任意的，都有H(M)() = cl()的充分必要条件是对于任意的C()都有|| = 2。

本文中给出了两种构造：从关系诱导出一个邻域拟阵，从拟阵产生一个关系。因此，一个拟阵可以诱导出一个关系，这个关系紧接着可以诱导出一个相应的拟阵。类似地，一个关系可以诱导出一个拟阵，这个拟阵紧接着诱导出一个关系。那么原来的拟阵和诱导出的新拟阵以及原来的关系和诱导出的新关系之间有什么样的联系呢？

定理 2 设是上的一个关系，()是由关系诱导的邻域拟阵，且(())是由拟阵()的诱导的粗糙集，则有

(()) = {(,)×:S() =S()}。 （17）

证明根据式（14）可知C(()) = {{,}:,S() =S()}。根据式（15）的概念，有(())=或{,}C(())S() =S()。

定理 3设是上的一个拟阵，()是拟阵的诱导的关系粗糙集，且(())是由关系()诱导出的邻域拟阵。那么(()) =的充分必要条件是对任意的C()，都有|| = 2。

4 结语

本文从关系中邻域概念的角度创建了关系粗糙集的邻域拟阵，研究了其相关集、极小圈、秩函数和闭包算子等特性。为了更深层的了解邻域拟阵，给出了从拟阵到关系的逆构造方法，并进一步研究了这两种构造方法之间的关联。

[1] 耿素云, 屈婉玲, 王捍贫. 离散数学教程[M]. 北京大学出版社, 2009.

[2] 赖虹建. 拟阵论[M]. 高等敎育出版社, 2002.

[3] Lin T Y. Topological and fuzzy rough sets[M]//Intelligent Decision Support. Springer Netherlands, 1992: 287-304.

[4] Liu Y, Zhu W. Matroidal structure based on serial and transitive relations[J], Journal of Applied Mathematics, 2012: (2012): Article ID 429737, 16 pages.

[5] Marek V W, Skowron A. Rough sets and matroids[J]. Transactions on Rough Sets XVII. Springer Berlin Heidelberg, 2014: 74-81.

[6] Pawlak Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5): 341-356.

[7] Wybraniec-Skardowska U. On a generalization of approximation space[J]. Bulletin of the Polish Academy of Sciences. Mathematics, 1989, 37(1-6): 51-62.

[8] 史忠植. 知识发现[M]. 清华大学出版社, 2002.

[9] Zadeh L. Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J]. Fuzzy Sets and Systems, 1997, 90(2): 111-127.

[10] Zakowski W. Approxiamtions in the space[J]. Demonstratio Mathematica, 1983, 16: 761-769.

[11] Zhang S, Wang X, Feng T, et al. Reduction of rough approximation space based on matroid[M]//Machine Learning and Cybernetics (ICMLC), 2011 International Conference on. IEEE, 2011, 1: 267-272.

[12] Zhu W, Wang S. Rough matroids based on relations[J]. Information Sciences, 2013, 232: 241-252.

[13] Zhu W. Generalized rough sets based on relations[J]. Information Sciences, 2007, 177(22): 4997-5011.

Neighborhood Matroid of Relation-Based Rough Set

LIU Yanfang*, CHEN Xueyun

(Institute of Information Engineering, Longyan University, Longyan Fujian 364000, China)

For a relation on a universe, a family of subsets is defined through neighborhood, and then is proved to satisfy the independence axiom of matroids, based on which, we propose a neighborhood matroid of relation-based rough sets. In order to study this type of matroids, we research its circuit, rank function and closure operator. Meanwhile, we propose another construction which is from a matroid to a relation, and investigate the relationship between the upper approximation of the relation and the closure of the matroid. Furthermore, we study the connection between a relation and a new relation induced by the matroid which is induced by the original relation. Especially, the new relation can be equally expressed by the original relation.

granular computing; relation-based rough set; upper approximation; neighborhood; matroid

1672-9129(2016)02-0006-05

TP18

A

2016-09-10；

2016-09-21。

国家自然科学基金面上项目（61379049），龙岩学院百名青年教师攀登项目（LQ2015031），龙岩学院协同创新项目（张凌）；大学生创新创业训练计划项目（S20141004）。

刘艳芳(1987-)，女，河南省濮阳市，龙岩学院教师，研究生，主要研究方向：粗糙集与粒计算、人工智能和机器学习；陈雪云(1976-)，女，福建省漳平市，龙岩学院副教授，硕士，主要研究方向：数据挖掘、模式识别和机器学习。

(*通信作者电子邮箱liuyanfang003@163.com)