期望序信息系统的优势粗糙集模型

刘真勃，代建华，张其来，高帅超，石红



期望序信息系统的优势粗糙集模型

刘真勃，代建华*，张其来，高帅超，石红

(天津大学计算机科学与技术学院，天津300350)

对在实际应用中，信息系统的属性通常具有期望，比如量器的测量误差、产品质量标准、医疗生理指标等，为此本文定义了期望序信息系统，在一定程度上将无期望的序信息系统推广为期望序信息系统，并在期望序信息系统的基础上，构建了基于距离的优势关系，使用辨识矩阵的方法进行了属性约简，最后经过实例证明方法简单可行。

粗糙集；期望序信息系统；优势关系

引言

粗糙集理论[1]是一种处理不确定、不完备、不一致数据的数学工具。近年来，粗糙集理论引起了国内外学者的广泛关注和研究, 应用在决策制定、模式识别、数据挖掘等领域。经典粗糙集理论以等价关系为基础，没有考虑属性的偏好关系。Greco等人[2, 3]针对准则属性的偏好关系问题，采用优势关系代替等价关系，为序信息系统的发展奠定了基础。采用有效的排序方法是序信息系统的重要内容，许多学者采用不同的排序方法建立了多种优势关系[2-7]。文献[2,7]提出属性值越大优势越大的排序方法，建立优势关系；Qian等人[4]利用有序区间值信息系统的属性值有上界和下界的特点，提出了比较两个区间值上界和下界数值大小的优势关系；Yang等人[5]将不完备区间值信息系统转化为完备信息系统，再采用文献[4]方法构建优势关系的方法进行了研究；于莹莹[8]和杨青山[9]等人对区间值序信息系统提出了可能概率的排序方法建立优势关系，并用分辨矩阵方法进行了属性约简；曾雪兰等人[10]提出了比较区间值半径和中心的排序方法，构建优势关系。

上述排序方法的偏序关系都认为属性值越大越优或者越小越优，忽略了属性值有固定期望值的情况。现实世界里，由于喜好的存在和对事物属性的经验性认知，人们对大部分的事物属性都有一定程度的期望，期望可能是越大越好的或者越小越好的基本描述，也可能是某个具体数值。对于含有期望属性的有序信息系统，传统的优势关系无法获得与现实需求一致的分类与属性约简。例如某公司生产的便携式电子秤的测量误差的期望值是0，三个电子秤1;2;3的测量误差分别为：2，-1，-3。根据数值越小越优排序方法，它们的偏序关系应该是3最好，2次之，1最差，在实际的质量检测中，考虑产品测量误差与期望值之间的差距，真实的偏序关系是2最好，1次之，3最差。针对实际应用中，属性具有期望的特点，本文定义了期望序信息系统，构造了期望优势关系，并在一定范围内将期望的概念推广至传统的序信息系统，应用辨识矩阵的方法进行了属性约简。

论文结构安排如下：第2节介绍序信息系统的基础知识和常见的优势关系；第3节定义期望序信息系统和基于距离的优势关系；第4节期望序信息系统的近似空间和属性约简方法；第5节进行实例分析；最后总结全文。

1 序信息系统的基本概念

本节回顾一般序信息系统的基本概念，分析序信息系统中常见的几种优势关系。

定义1[6]信息系统是一个四元组，其中是非空有限的对象集，称为论域；是非空有限的属性集；，是属性值的集合，是属性值；是信息函数，，若表示对象在属性上的取值。

Pawlak粗糙集理论的信息系统中，属性集决定了信息系统的等价关系。在实际中，在考虑决策者偏好的情况下，很多属性需要按照属性值递增或者递减的偏序关系确立优势关系。

定义2[6]设信息系统=<,,,>，，∈，表示在属性下至少与一样好，若属性的值域中有偏序关系，则称是准则属性。对于信息系统中的任意属性都是准则属性，则称该信息系统为有序信息系统。

定义3[6]设有序信息系统=<,,,>，，,令，则称是有序信息系统上的一个优势关系。

桂现才等人[11]使用单值信息系统中的优势关系如下：

Shao等人[12]在不完备信息系统中定义优势关系如下：

(2)

注：f(x)=*在信息系统中表示该属性值缺失并且用*表示。

Qian等人[4]提出了区间值信息系统的一种优势关系如下：

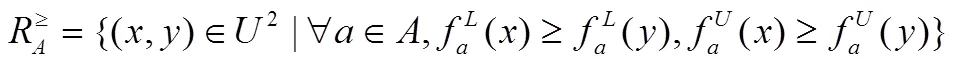
从以上优势关系可以看出，研究者只考虑了数值越大越优的偏序关系，忽略了部分属性不是数值越大越好，也不是数值越小越好，而是越接近某个期望值越好。例如企业批量生产定重为1千克的袋装面粉时，期望每袋面粉的重量为1千克，实际每袋面粉的重量在1千克左右浮动，一般认为面粉重量越接近1千克越符合企业利益。一般的信息系统无法准确体现属性具有期望的特点，上述的优势关系不能处理具有期望值的信息系统。因此，定义一个具有期望值的信息系统是有必要的。

2 期望序信息系统及其优势关系模型

本节主要定义了期望序信息系统，分析对象属性值与期望值之间的关系，定义基于距离的优势关系，在一定程度上对期望进行了推广。

定义4期望序信息系统是一个五元组={}，其中是非空有限的对象集，称为论域；是非空有限的属性集；是属性值和期望值的集合，是属性的值域，是属性期望值的值域，表示期望值为的属性，表示属性的期望值为；是信息函数，，若,表示对象在期望值为的属性下的值，本文也简写为。

从定义可以看出，期望序信息系统是在一般的序信息系统增加了期望值，属性具有期望值的特点。表1是一个期望序信息系统，对象集为{123456},属性集为={1,2,3, a,5,6},从中可得a的期望值为2，。

表1 期望序信息系统

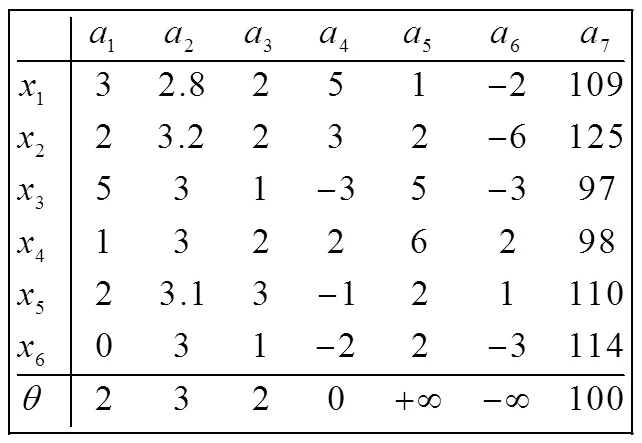
属性值与期望值的分布的情况如图1所示：f(),f(),f(),f()是期望值为的属性上的四个不同的取值，具体情况有以下三种。

（1）属性值f()与f()离属性的期望值的距离相等，即()()，此时认为在属性下与优势相等（或者等价)；（2）属性值f()比f()距离属性的期望值更近，即()(), 此时认为在属性下比更优；（3）属性值f()比f()距离属性的期望值更远，即()()，此时认为在属性下比差。因而，四个属性值按照从优到劣的偏序是：。

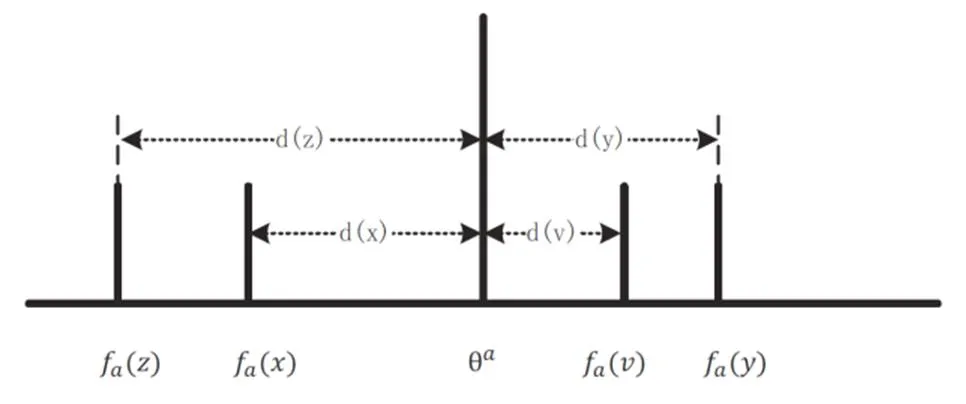
图1 属性值与期望值的位置关系

在有期望的属性中，数值越接近期望值就越优，因此需要充分利用期望值进行构建偏序关系。

定义5 设期望序信息系统={}，，，与期望值的接近程度表示为：。若，则称在期望值为的属性下不比差，记作。

在这种偏序关系下，优势关系和优势类可以定义为：

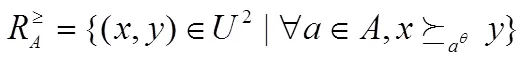
从定义容易证明：期望优势关系具有自反性和传递性，而不具有对称性。优势关系的具体意义为：对象的距离越小，则越接近期望值，优势越大，符合设定期望值的实际。

为区分等式(1)和等式(4)两种优势关系，本文将文献[11]中的优势关系（等式1）称为经典优势关系，优势关系和优势类分别表示为，等式4表示的优势关系称为期望优势关系，优势关系和优势类分别表示为。

性质 1设期望序信息系统={}，，,∈，经典优势关系可以转化为期望优势关系。

证明 经典优势关系可以理解为数值越大越优，本文认为数值越大越优的属性期望为。为了计算方便简单，取一个足够大的数值将期望从替换为固定数值，本文选取替换为。

3 期望序信息系统的粗糙集方法

3.1 近似空间

定义6 设期望序信息系统={},，,是期望优势关系，上、下近似和边界域定义为：

示例1 信息系统如表1所示，设={a, a}，={x, x}, 等价类可以表示为：={ x};={ x, x, x};= { x};={ x, x, x};={ x, x, x, x, x, x};= { x, x}。上近似、下近似和边界域分别为：，={x},={ x, x,}。

3.2 属性约简

某些概念只需要信息系统的部分属性就能表达，因此信息系统中往往存在大量数据冗余。在粗糙集理论中，通过属性约简可以得到属性冗余较少的数据集，提高知识发现的效率。

定义7={},是期望优势关系，若是信息系统的一个约简，记作()，当且仅当满足以下两个条件：

系统中可能存在多个属性约简，所有属性约简的交集就构成了信息系统的核，记作。

辨识矩阵[13]是Skowron提出的，是属性约简的重要方法之一。辨识矩阵具有容易理解，操作简单的优点，许多学者研究了辨识矩阵在属性约简上的应用。

定义8[10,14]设期望序信息系统={},是期望优势关系，分辨矩阵表示为：

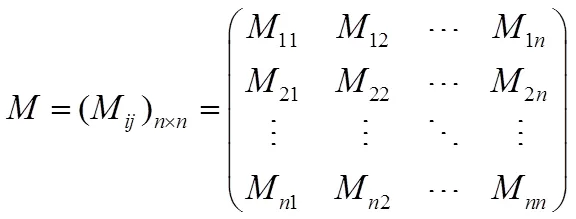
定理 1期望序信息系统={}，是在期望关系下的一个约简，当且仅当是满足，的最小属性集。

假设是的一个约简，且存在, 使得, 则有且，与是的一个约简矛盾；同时，对于任意=-{}，都不能得到，因此是满足的最小属性集。

定义9 设期望序信息系统={}，是期望优势关系下的可辨识属性集，称为可辨识函数, 其中是指与相对应的布尔值。

定理 2 设期望序信息系统={}，是的一个约简，当且仅当是辨识函数转化为析取式的一个基本蕴涵。

其中() 是表示集合的秩。

根据分辨矩阵和分辨函数的定义，基于距离的优势关系的属性约简算法如下：

输入：有期望的信息系统={}

输出：属性约简

步骤1 将期望值为+∞和-∞的属性的期望分别替换为属性值域的上确界和下确界；

步骤2由优势关系计算可辨识属性集M和可辨识函数；

步骤3计算可辨识函数，从合取式转化为析取式；得到每一个基本蕴涵就是一个属性约简集。

4 实例分析

本节以某公司生产的便携式电子秤质量检测信息为例，将一般序信息系统转化为期望序信息系统，并进行属性约简。

表2 关于便携式电子秤的期望信息系统

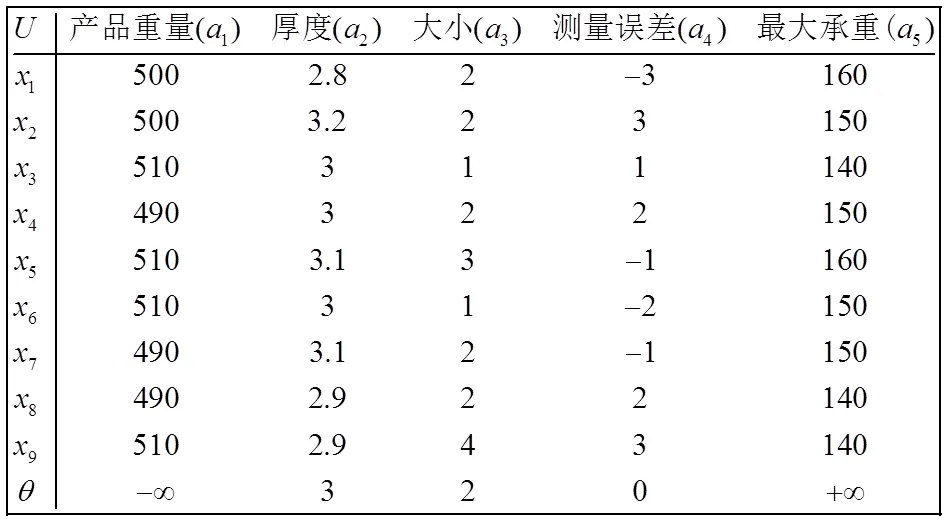
表2是一个关于便携式电子秤的期望序信息系统，论域{x, x, x, x, x, x, x, x, x}代表抽检的9个产品；,属性集为={a, a, a, a, a}表示电子秤的相关信息，分别是重量、厚度、大小、测量误差和最大承载重量。其中产品质量检测的标准是重量越小越好，最大承载重量越大越好，测量误差、厚度、大小的期望分别为：0，3，2。因为属性a和属性a的期望都是无穷的，需要计算替代期望值，此例中选取属性a值域的下界和属性a的上界作为替代期望值。

设={a},={a}，经典优势关系在属性集下的优势类为：

表3 关于便携式电子秤的辨识矩阵

期望优势关系在属性集下的优势类为：

经典优势关系在属性集下的优势类为：

期望优势关系在属性集下的优势类为：

从上面可以看出，对于属性集，经典优势关系和期望优势关系的得出的优势关系类是相同的，即两者在期望为+∞的属性的分类能力是相同的；而对于具有期望属性集，经典优势关系无法得到实际需求的分类，例如f4(1)=-3与f4(2)=-3，显然两者在期望为0的情况下两者的优势对等的，经典优势关系将两者进行了“错误”的分类，而期望优势关系能够很简单的获得实际希望的分类。

期望序信息系统关于期望优势关系在属性集的优势类为：

由定义8可得可分辨矩阵如表3所示。可辨识函数化简后可得

5 结语

在实际中，序信息系统中部分属性具有期望值的特性，因此分析期望序信息系统具有一定的意义。论文定义了基于距离的优势关系，并将一般序信息系统在一定程度上转化为期望序信息系统，解决了传统的优势关系无法处理期望序信息系统的问题，同时用辨识矩阵的方法进行了属性约简，并用实例证明方法简单可行。

[1] PAWLAK Z. Rough Sets [J]. International Journal of Computer & Information Sciences, 1982, 11(5):341–356.

[2] GRECO S, MATARAZZO B, SLOWINSKI R. Rough Approximation by Dominance Relations [J]. International Journal of Intelligent Systems, 2002, 17(2):153–171.

[3] GRECO S, MATARAZZO B, SLOWINSKI R. Rough Approximation of a Preference Relation by Dominance Relations [J]. European Journal of Operational Research, 1999, 117(1):63–83.

[4] QIAN YH, LIANG JY, DANG CY. Interval Ordered Information Systems [J]. Computers & Mathematics with Applications, 2008, 56(8):1994–2009.

[5] YANG XB, YANG JY, WU C, et al. Dominance-based Rough Set Approach and Knowledge Reductions in Incomplete Ordered Information System [J]. Information Sciences, 2008, 178(4):1219–1234.

[6] 徐伟华. 序信息系统与粗糙集[M]. 科学出版社, 2013.

[7] 徐伟华, 张文修. 基于优势关系下的协调近似空间[J]. 计算机科学, 2005, 32(9):164–165.

[8] 于莹莹, 曾雪兰, 孙兴星. 优势关系下的区间值信息系统及其属性约简[J]. 计算机工程与应用,2011, 47(35):122–124.

[9] 杨青山, 王国胤, 张清华等. 可变精度优势关系下的析取集值有序信息系统[J]. 广西师范大学学报: 自然科学版, 2010, 28(3).

[10] 曾雪兰, 陈胜, 梅良才. 区间序信息系统及其属性约简算法[J]. 计算机工程, 2010, 36(24):62–63.

[11] 桂现才. 优势关系下序信息系统的信息量与粗糙熵[J]. 计算机工程与设计, 2008, 29(24):6340–6343.

[12] SHAO MW, ZHANG WX. Dominance Relation and Rules in an Incomplete Ordered Information System [J]. International Journal of Intelligent Systems, 2005, 20(1):13–27.

[13] SKOWRON A, RAUSZER C. The Discernibility Matrices and Functions in Information Systems [J].Theory & Decision Library, 1992, 11:331–362.

[14] DAI JH, TIAN HW. Fuzzy Rough Set Model for Set valued Data [J]. Fuzzy Sets and Systems, 2013,229:54–68.

Rough Set Model Based on Dominance Relation for Ordered Information Systems with Expectations

LIU Zhenbo, DAI Jianhu, ZHANG Qilai, GAO Shuaichao, SHI Hong

(School of Computer Science and Technology, Tianjin University, Tianjin 300350, China)

In real world applications, the attributes with expectation, such as the measurement error, the quality standards of products and biological indicators for medical treatment, should be considered by decision makers. Therefore, the concept of ordered information system with expectations is proposed. Moreover, we extend the general ordered information systems to ordered information systems with expectations based on the dominance relation by the distance between the expectation and the real value. Consequently, attribute reduction of an ordered information system with expectations is investigated by discernibility matrix. Finally, an example illustrates that the method is simple and feasible.

rough sets; ordered information system with expectations, dominance elation

1672-9129(2016)02-0001-05

TP18

A

2016-08-28；

2016-09-21。

国家自然科学基金资助(No.61473259， No.61502335)。

刘真勃，男,硕士研究生，研究方向：软计算、机器学习；代建华，男，教授、博士生导师,主要研究方向：人工智能、粗糙集、模糊集、机器学习、数据挖掘、智能信息处理，E-mail：david.joshua@qq.com；张其来，男，硕士研究生；高帅超，男，硕士研究生；石红，女，副教授。

(*通信作者电子邮箱：david.joshua@qq.com)