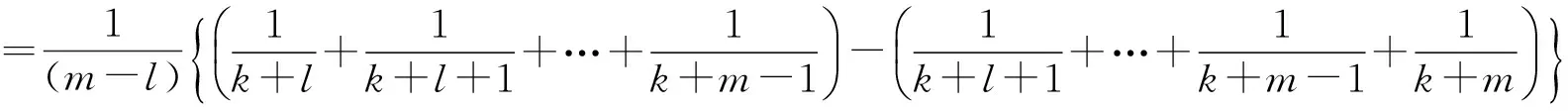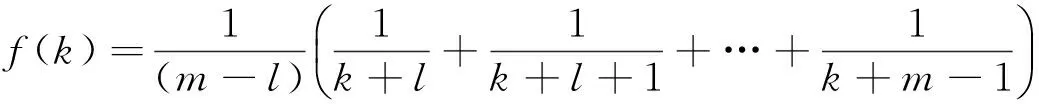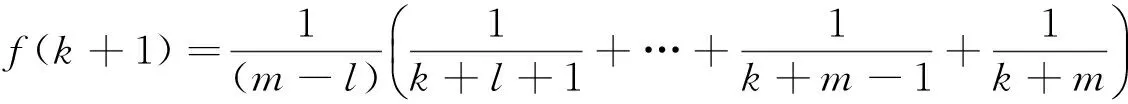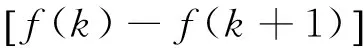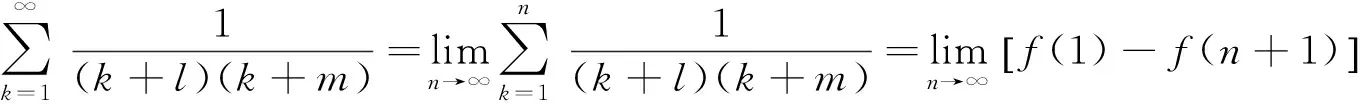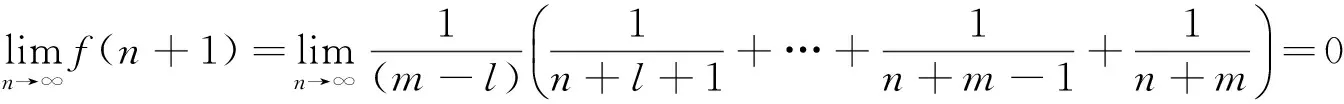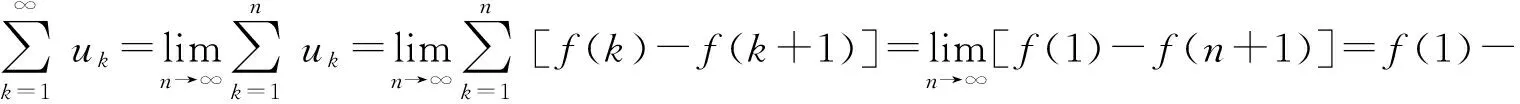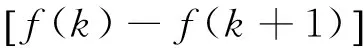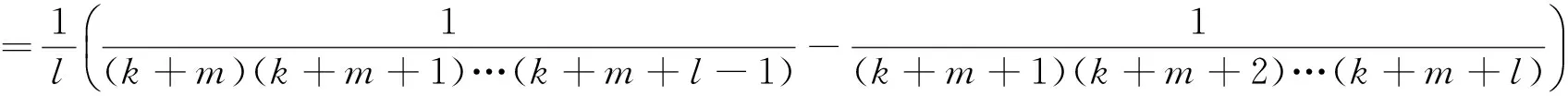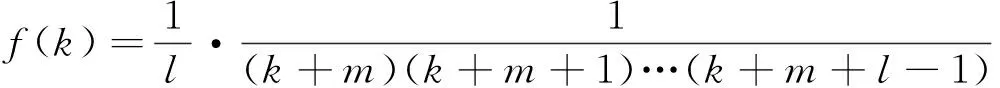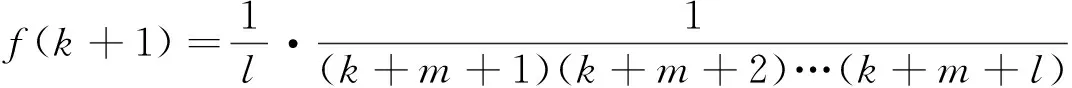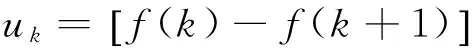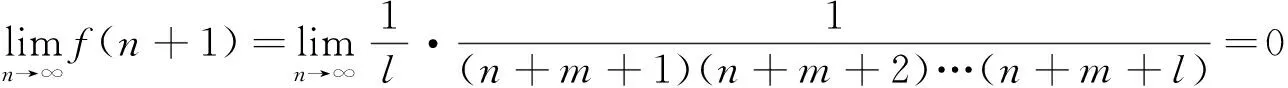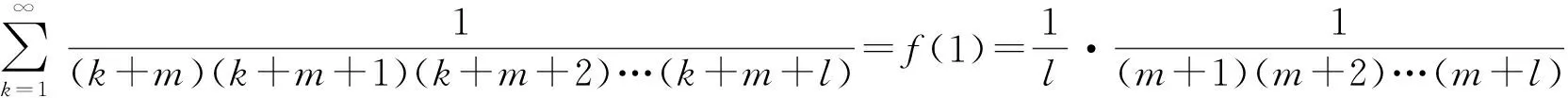一类级数求和的推广之注记
刘春平
(扬州大学数学科学学院,江苏扬州225002)
一类级数求和的推广之注记
刘春平
(扬州大学数学科学学院,江苏扬州225002)
通过对文献[1]中结论的分析,进一步阐述了拆项技巧在级数求和中的应用.
级数; 和; 通项
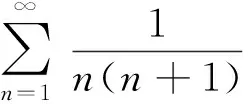
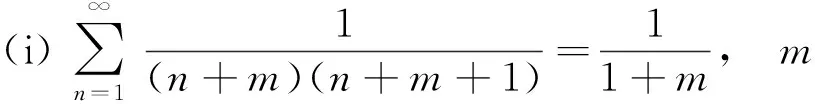
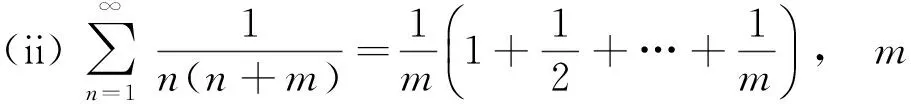
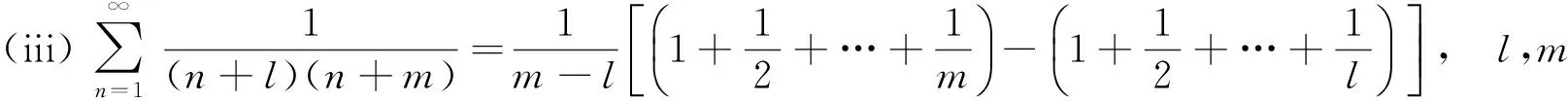
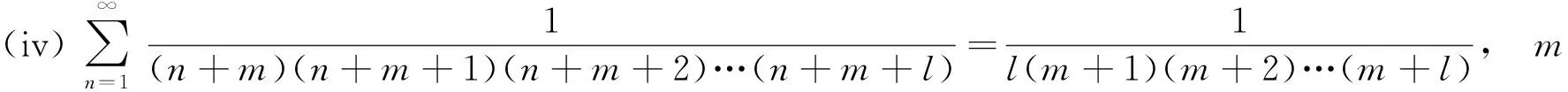
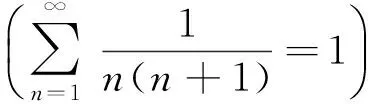
注意到(i)是(iv)的特例,(ii)是(iii)的特例,所以只需要分析(iii)和(iv).
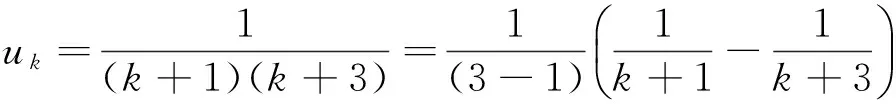
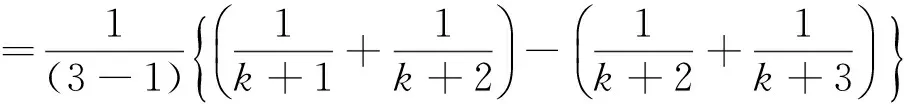
(1)
记
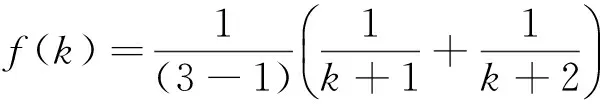
(2)
则
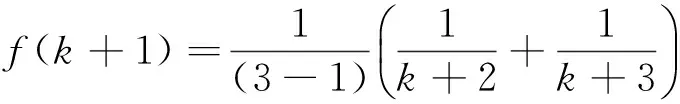
(3)
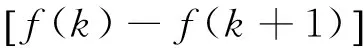
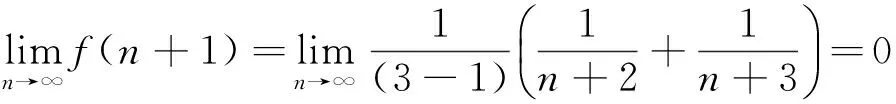
有
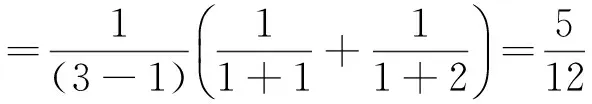
(4)
推广到一般情形
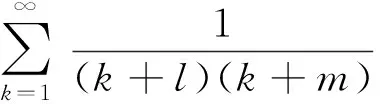
(5)
其中l为非负整数,m为正整数且l (6) 记 (7) 则 (8) (9) 再注意到 有 (10) (10) 式就是情形(iii). 通过上述分析,可以归纳一下拆项技巧在级数求和中的应用: (11) (12) 其中m为非负实数,l为正整数.注意到 (13) 记 (14) 则 (15) 有 (16) (16) 式就是情形(iv). 综之,我们用拆项求和的技巧给出了文献[1]中结论的导出过程. [1]薛凌霄,李德新. 一类级数求和的推广[J]. 大学数学,2015,31(3):86—89. [2]程海来. 一类无穷级数的求和[J]. 大学数学,2013,29(3):112—114. [3]同济大学数学系.高等数学下册 [M]. 6版. 北京: 高等教育出版社,2007: 249. A Note on the Generalization of a Class of Infinite Series Summation LIUChun-ping (Institute of Mathematics, Yangzhou University, Yangzhou Jiangsu 225002, China) By analyzing the conclusions in literature [1], it has been further illustrated how the term-disassembling techniques are applied in the summation of infinite series. infinite series; summation;general term 2016-01-25;[修改日期]2016-03-28 江苏高校品牌专业建设工程资助项目(PPZY2015B109);扬州大学教改项目 刘春平(1964-),女,博士,教授,从事微分方程研究.Email:liucp@yzu.edu.cn O173.1 C 1672-1454(2016)03-0094-03