概率密度函数连续和不连续两种不同假设下的解题比较

胡吉卉，　吴　莺，　刘继成

(华中科技大学数学与统计学院，武汉430074)



概率密度函数连续和不连续两种不同假设下的解题比较

胡吉卉，吴莺，刘继成

(华中科技大学数学与统计学院，武汉430074)

概率密度函数连续的随机变量仅是一类特殊的连续型随机变量，因此假设概率密度函数连续是一个苛刻的限制.本文在随机变量概率密度函数连续和不连续两种不同假设下比较了两个典型例题的证明，可以看出两者的思路是完全不同的，后者通常更具有普遍性.

连续型随机变量； 概率密度函数； 矩母函数； 指数分布

1　引　　言

众所周知，连续型随机变量的概率密度函数有时是不连续的，只要不影响其积分的值甚至可以随意改变在一些点上密度函数的定义.因此，具有连续概率密度函数的随机变量仅是一类非常特殊的随机变量，假设概率密度函数连续则是一个非常苛刻的条件.因此，如果增加了概率密度函数连续的假设，往往使要处理的问题变得特殊.本文将从两个具体例子出发，比较在概率密度函数连续和不连续两种不同假设下证明方法的异同.

2　例1解题比较

两个随机变量独立的定义是联合分布函数等于两个边缘分布函数的乘积.但是，通常概率论教材(见[1] P.50的(3))中提到连续型随机变量情形时会直接给出结论：两个连续型随机变量独立等价于联合密度函数等于两个边缘密度函数的乘积.因为这里是函数的相等，若要求概率密度函数在每点都相等显然太强了,也是不必要的.事实上，只要在除去Lebesgue测度为零的集合之外两者相等就能说明这两个随机变量是独立的.注意到这一点后，利用该等式证明两个随机变量独立一般是容易处理的.

另一方面，我们也经常会遇到相反的问题.假设两个连续型随机变量独立，然后需要证明他们拥有某些性质.此时，两个随机变量独立的条件告诉我们的信息自然也只能是：联合密度函数在几乎处处意义下等于两个边缘密度函数的乘积.如果联合密度函数以及两个边缘密度函数都是连续的，则可以推出该等式是对每点都是成立的.考察下面的例子(参见[4] P.91例3.10).

证1仅证明必要性，充分性容易直接验证.二维正态分布的密度函数为

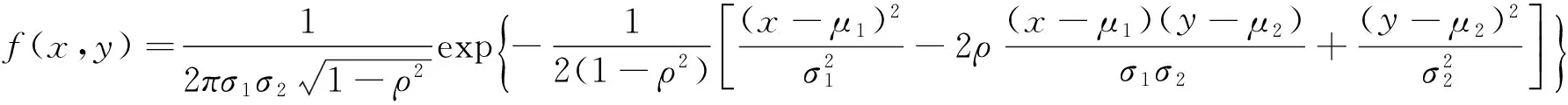
两个边缘分布为

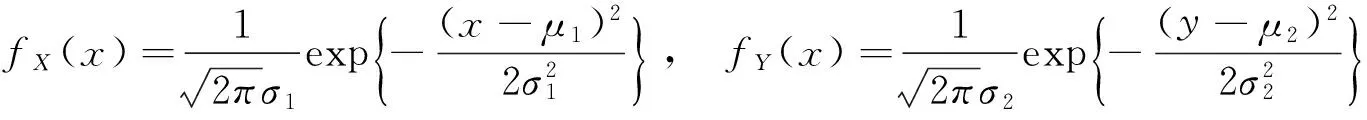
注意到这三个函数是连续的，则X和Y独立蕴含

f(x,y)=fX(x)fY(y)

对所有的x,y∈成立.特别地，f(μ1,μ2)=fX(μ1)fY(μ2)，因此

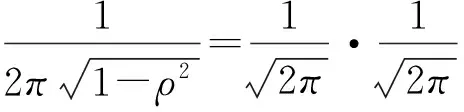
易知ρ=0.

下面考虑的问题是，如果不用密度函数连续的性质，如何证明例1的结论呢？见下面的证明.

证2令

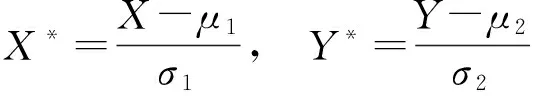
则X*和Y*独立，且E(X*)=E(Y*)=0.因此E(X*Y*)=E(X*)E(Y*)=0.另一方面，直接计算

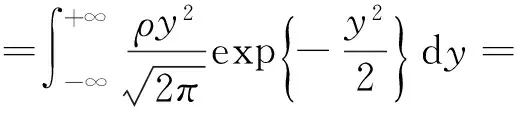
因此ρ=0.

3　例2解题比较

例1中我们事先知道随机变量具有连续的概率密度函数，因此例1中证1的证明也是可行的.然而，通常的情形是，事先并不知道假设中的概率密度函数是否连续，此时就不能直接将联合密度函数在每点都等于两个边缘密度函数乘积作为条件来使用.事实上，在没有概率密度连续的假设下，有关概率密度的等式都只能理解为几乎处处意义下成立，考察下面的例子.

例2设X和Y为取非负实值的连续型随机变量，且相互独立.若对任意u>0，在给定X+Y=u的条件下，X服从[0,u]上的均匀分布，证明X和Y都服从指数分布.

证1增加假设：X和Y的密度函数在[0,+∞)上连续.

第1步：设X和Y的概率密度函数分别为fX(x)和fY(y)，则(X,Y)的联合密度函数为fX(x)fY(y).做变换

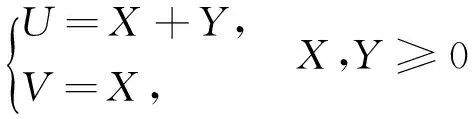
则逆变换为

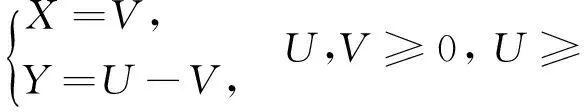
此变换的Jacobi矩阵的行列式为

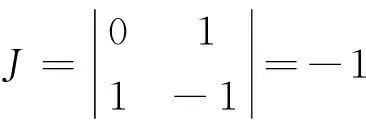
因此(参见[2]P.169)，(U，V)的联合密度函数为

fU,V(u,v)=fY(u-v)fX(v),u,v≥0, u≥v.

因此，在给定U=u条件下V的条件密度函数为

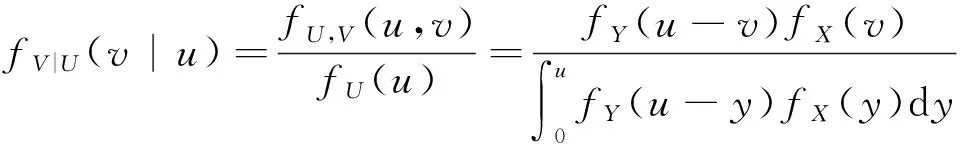
(1)

第2步：由假设

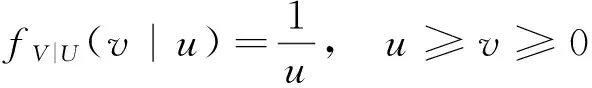
等式(1)以及密度函数的连续性得

(2)

对所有的u≥v≥0成立.注意到，等式(2)右边仅与u有关，与v无关.因此，对每个u≥0

fY(u-v)fX(v)=fY(u-v′)fX(v′),∀0≤v,v′≤u.

特别地，令v′=0和v′=u得

fY(u)fX(0)=fY(0)fX(u)=fY(u-v)fX(v),0≤v≤u.

(3)

(3)的第一个等式表明，fX(u)与fY(u)最多仅相差一个常数的倍数.因为它们都是密度函数，由密度函数的规范性，有

fX(x)=fY(x),x≥0.

亦即X和Y同分布.

第3步：令

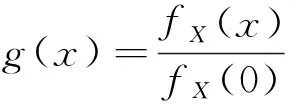
则g(0)=1，且g连续.由(3)的第二个等式知，g满足

g(u-v)g(v)=g(u),0≤v≤u.

令x=v,y=u-v，则

g(x+y)=g(x)g(y),x,y≥0,g(0)=1.

该方程的唯一解为g(x)=e-λx，故fX(x)=fX(0)e-λx,x≥0.最后，注意到密度函数的规范性，得

fX(x)=λe-λx,x≥0.

其中λ=fX(0).所以X与Y均服从参数为λ=fX(0)的指数分布.

若去掉例1上面证明中fX(x)和fY(y)连续的假设，则等式(1)只是对几乎处处u≥v≥0成立，所以等式(2)在v=0和v=u这两个特殊点的值可能是不相等的，无法得到关键的等式(3).因此，上面的证明思路是行不通的.为此，我们将选用矩母函数的方法给予证明.

证2不需要假设：X和Y的密度函数在 [0,+∞)上连续.

第1步： 证明X和Y同分布.因为对任意u>0在给定X+Y=u的条件下，X服从[0,u]上的均匀分布，所以

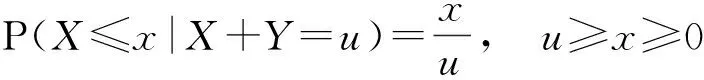
因此，对任意u>0，在给定X+Y=u的条件下，Y的分布函数为

P(Y≤y|X+Y=u)=P(u-X≤y|X+Y=u)

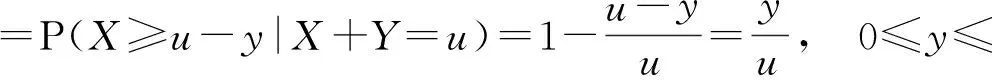
亦即，对任意u>0，在给定X+Y=u的条件下，Y也服从[0,u]上的均匀分布.因此(X,X+Y)与(Y,X+Y)有相同的联合分布.特别地，它们的边缘分布相同，因此X和Y同分布.

第2步： 因为X和Y同分布，设X和Y的概率密度函数都为f(x)，分布函数为F(x).记U=X+Y,U的密度函数为fU(u), (X,U)的联合密度函数为fX,U(x,u),X关于U的条件密度函数为fX|U(x|u).由假设，则(X,U)的联合密度函数为

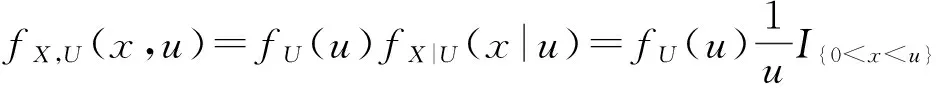
因此

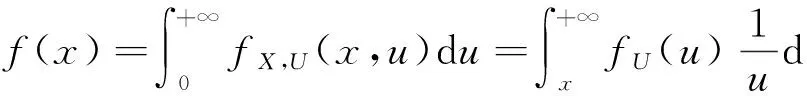
(4)

第3步： 记X的矩母函数为φ(t),U的矩母函数为φU(t)，则(参见[3]P.248)

φU(t)=φ2(t).

(5)

另一方面，由等式(4)并交换积分次序，有

(6)

其中

(7)

为常数.改写(6)最后一个等式中的积分，并交换期望和积分次序，再由矩母函数的定义及等式(5)，有

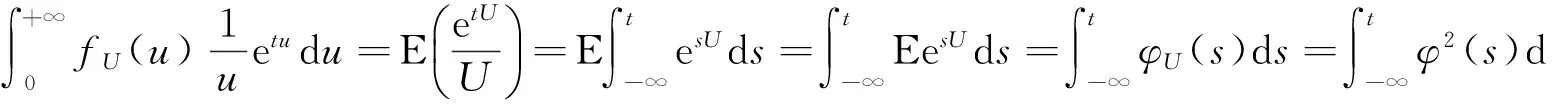
代入(6)式得

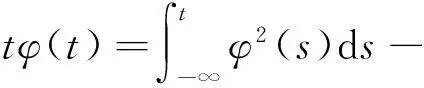
(8)

第4步： 记Φ(t)=tφ(t).对(8)式两边关于t微分有

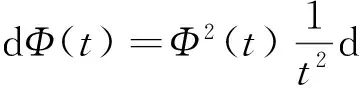
分离变量得

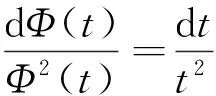
两边积分得

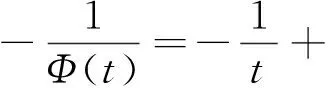
因此

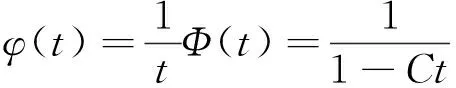
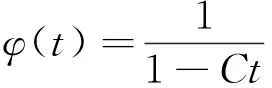
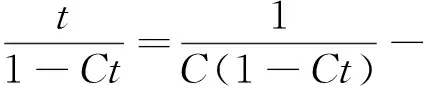
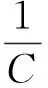
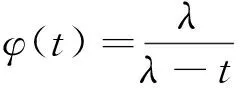
φ(t)与参数为λ的指数分布的矩母函数形式一致(参见[3]P.246例6c).因为随机变量的矩母函数和分布是一一对应的(参见[3]P.248)，所以X和Y都服从参数为λ指数分布.

注若函数f(x)连续，(4)式和(7)式说明λ=f(0)，这与证1结果一致.但若f(x)不连续，X和Y分布的参数则由(7)式决定.

4　结　　论

连续型随机变量的概率密度函数有时是不连续的，具有连续概率密度函数的随机变量仅是一类特殊的随机变量，所以假设概率密度函数连续是一个非常苛刻的条件，其证明方法不具有一般性.在没有概率密度连续的假设下，有关概率密度的等式都只能理解为几乎处处意义下成立，此时变通的方法通常是选用分布函数、数字特征、矩母函数或者特征函数作为替代的证明工具.

特别地，两个连续型随机变量独立等价于联合密度函数在几乎处处的意义等于两个边缘密度函数的乘积.因此，若要通过该等式证明两个随机变量独立，我们可以允许在Lebesgue测度为零的集合之外等式不成立.反之，当用两个连续型随机变量独立作为条件时，尽管可能要证明的结果中密度函数的确是连续的，我们通常也不能事先使用联合密度函数在每点都等于两个边缘密度函数乘积的等式.

[1]刘次华.概率论与数理统计[M]. 2版. 武汉：华中科技大学出版社， 2012.

[2]李贤平.概率论基础[M].3版. 北京：高等教育出版社， 2010.

[3]Sheldon Ross.概率论基础教程[M].6版. 北京：机械工程出版社， 2006.

[4]华中科技大学数学系.概率论与数理统计[M].2版.北京：高等教育出版社， 2003.

The Comparisons of Examples Under Continuous and Discontinuous Assumptions for Probability Density Function

HUJi-hui，WUYing，LIUJi-cheng

(School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan 430074, China)

The random variable with continuous probability density function is only a special kind of continuous random variables, so the assumption that random variable has a continuous probability density function is very strict. In this paper, we give a comparison of the proofs for two typical examples under continuous and discontinuous assumptions, it shows that these two methods are completely different, the latter usually has more universality.

continuous random variable; probability density function; moment generating function; exponential distribution

2015-11-13；[修改日期] 2016-03-09

华中科技大学教学研究项目(2015067)，华中科技大学自主创新研究基金(2014TS066)

胡吉卉(1976-),女，博士，副教授，从事概率统计研究.Email: hujihui@hust.edu.cn

吴莺(1979-),女，博士，讲师，从事概率统计研究.Email: yingwu@hust.edu.cn

O172.2

C

1672-1454(2016)03-0106-05