基于频域分段-时域反演法的抽水蓄能机组大波动过渡过程水压脉动信号分析

寇攀高，邓 磊，刘 平，吴长利



基于频域分段-时域反演法的抽水蓄能机组大波动过渡过程水压脉动信号分析

寇攀高1，邓 磊2，刘 平3，吴长利1

(1. 国网湖南省电力公司电力科学研究院，长沙 410007；2. 国网新源控股有限公司技术中心，北京 100161；3. 国网新源湖南黑麋峰抽水蓄能有限公司，长沙 410213)

抽水蓄能机组大波动过渡过程中水压脉动信号包含大量的毛刺，表现出瞬时大幅跳变的特点，严重影响水压脉动最值的分析选择。针对该问题，本文提出一种频域分段-时域反演法，首先将时域水压脉动信号进行傅里叶变换以获取水压脉动信号的频谱特征，在频域根据设置的截止频率对水压脉动信号滤波，经快速傅里叶逆变换反演出滤除指定频段后的水压脉动信号。通过在频域滑动截止频率，提取水压脉动极值-滑动截止频率关系曲线，分析不同频段对水压脉动最值的敏感性，揭示滤波频率对水压脉动信号最值的影响。该方法应用于工程实际抽水蓄能机组水压脉动信号分析，为水压脉动最值的确定提供了有力论证。

抽水蓄能机组；压力脉动信号；频域分段-时域反演法；滑动截止频率

0 前言

准确测量水电机组过渡过程中水压脉动信号对评价水电机组的安全稳定运行有着重要意义。通常水压脉动信号作为调节保证的评价指标之一，在水电机组设计过程中提出严格的控制，然而工程实际测试中测量的水压脉动信号包含大量毛刺，水压脉动信号表现出非平稳、瞬时突变等特征，具体到工程实践中某一台机组时往往存在着大波动过渡过程水压脉动采样频率该如何选择、极值确定是否应该采用滤波、滤波截止频率如何选择等问题。

文献[1]~[3]应用交叉小波变换在时频空间中分析水轮机导轴承振动和尾水管出口、蜗壳进口、顶盖下等3个典型水压脉动之间的相关性，提取机组振动与水压脉动之间的相关性随时间和频率变化的特征，结果表明水压脉动以低频为主。文献[4]利用采样率转换技术、Hilbert—Huang变换等技术研究了机组起动过程中的尾水管水力压力脉动信号的时变特征，研究表明，水轮机尾水管中的水力压力脉动以低频为主。

上述研究深化了水压脉动信号低频部分或稳态分量的认识，缺乏对水压脉动信号瞬时突变的关注与深入研究。工程实践中，水电机组过渡过程的水压脉动最大值或最小值往往与毛刺伴随。某些情况下，可能出现毛刺值大于调保计算值或毛刺值低于调保计算值的情况。此类情形给蜗壳水压最大值、尾水管进口最小值的确定与评价带来了困难。一些观点认为毛刺多为噪声干扰、难以反应真实水压脉动最值，需要经过一定处理（如信号滤波、取置信度等方法）获取机组甩负荷过程中水压脉动最值。另一部分观点认为毛刺真实可靠，毛刺中水压脉动极值为真实的水压脉动值无须滤波。究竟实测水压脉动信号是否该加工处理？如果需要加工处理，应该采用何种方法？如果选择滤波方法，那么应该如何选择截止频率？

为了回答上述问题，本文以实测的抽水蓄能机组过渡过程水压脉动数据为研究对象，分析对比了取置信度、信号滤波的区别及适用场景，研究了基于FFT、IFFT的水压脉动信号滤波方法，提出了一种频域分段-时域反演法的水压脉动信号分析方法，通过利用该方法设置不同的截止频率并提取相应的水压脉动极值，构建了截止频率与水压脉动极值间的关系曲线，揭示了不同频率成分对水压脉动极值的影响，回答了是否应该选择滤波以及该如何选择滤波截止频率的问题，为水压脉动信号的滤波、极值的确认提供了理论支撑。

1 水压脉动最值确定方法

1.1 置信度方法

工程实践中取置信度时往往将所采集的个数据降序排序，然后按照一定百分比剔除个数值中较大值及较小值。例如：取97%置信度，工程中往往首先将数据降序排序，对排序的数据剔除1.5%个较大值、1.5%个较小值，剩余数据即认为是满足97%置信度的数据。

对于大波动过渡过程，水压脉动存在极大值、极小值，如果采用取置信度方法，水压脉动信号中的极大值、极小值显然被剔除，处理后信号中极值发生时刻、极值幅度均发生变化。因此，不宜使用取置信度方法处理过渡过程水压脉动信号。

1.2 滤波方法

滤波的方法很多，按照适用范围可以将滤波方法分为经典滤波和现代滤波[5]。经典滤波方法假设输入信号中的有用成分和希望去除的成分各自占据不同的频带，但信号和噪声的频谱相互重叠，那么经典滤波方法将不再适用。现代滤波方法主要是从含有噪声的时间序列中估计出信号的某些特征或信号本身，一旦信号被估计出，那么估计出的信号将比原信号具有更高的信噪比。

依据文献[1]~[3]的研究可知，水压脉动信号均为低频信号，经典滤波方法中的低通滤波主要有：Butter-worth、Chebyshew I、Chebyshew II、Elliptical、Bassel等方法。但这些方法存在着滤波器阶数选择、通道内存在波纹、相位特性不易控制等问题[4]，将该类滤波方法应用于水压脉动信号分析，发现滤波后的水压脉动信号存在一些失真，主要表现为：滤波后的信号起始数据波动幅度变大、信号极值发生时刻存在偏移。因此，不宜使用该方法对水压脉动信号展开分析。

2 频域分段-时域反演法

文献[5]研究表明，经典滤波方法中的低通滤波在通道、阻带间存在一个过渡区域，通带或阻带内存在波纹效应，另外在相位上随着频率增大相位滞后增大，相位上的滞后反应到时域波形中表现为水压脉动极大值发生时刻改变。为了避免该问题出现，本文利用快速Fourier正变换将时域信号转换到频域，获悉水压脉动信号时间序列中的频率成分及各频率成分的幅值，根据预设的截止频率将频域中某些频率成分幅值置零，然后利用Fourier逆变换将处理后的频域序列转换到时域。由于将某些频率幅值置零，其相位不会起作用，反应到时域波形中极值发生时不会发生偏移。

上述过程仅适用于某设定的截止频率，通过设置不同的截止频率，对原始水压脉动信号应用上述方法，可以获得不同截止频率下的时域波形，根据该波形可获得水压脉动极大值、极小值，且保证了极值发生时刻与原始信号极值发生时刻的同时性、不发生偏移。

2.1 快速傅里叶变换

对于周期为2的函数其Fourier级数表示为：

式中：

（1）由于所取的时间为无限长周期序列，周期为2，且时间只能取正值，将（-，）修改为(0,2)。

（2）式（1）中的对应于时间序列的时刻，即:。

（3）由于所处理的是离散的时间序列，积分替换为求和，即：，在（0,2）里等间隔取个采样点，取样时间间隔为:，其中。

按照上述映射修改后的式（1）表示为：

将式（2）代入式（1），式（1）的离散形式表示为：

式中：

将式（3）中的离散表达式中正弦函数和余弦函数合并后，可以得出下式：

2.2 滑动截止频率滤波

式（4）给出了Fourier变换的计算公式，根据式（4）中的C可以获得水压脉动信号的频谱幅值，相应的频谱值为kf,=0,1,2,…,/2,f=1/(△)，根据该频谱序列可以设置截止频率。根据采样频率可设置不同的截止频率为f(0≤f≤/2 f)，表示第个滑动截止频率。

2.3 最值-截止频率曲线

2.4 最值误差-截止频率曲线

图1给出了上述算法的流程图。

图1 频域分段-时域反演法流程

3 尾水管压力脉动信号分析

3.1 工程实例介绍

某电站地下厂房安装4台单机容量为300MW的单级混流可逆式水泵水轮机组，总装机容量为1200MW，机组其他参数见表1。电站上水库正常蓄水位为400m，下水库正常蓄水位为103.7m。引水系统采用一洞二机的布置方式，尾水系统采用一洞一机的布置方式。2014年电站4台机组先后开展了单机甩负荷试验及双机甩负荷试验。试验过程中使用多通道数据采集仪对13个水压脉动测点进行测量，将本文提出的方法应用于试验过程中，对于球阀后水压脉动极值、尾水管进口水压脉动极值分析，解决了水压脉动信号高频成分是否应该滤波以及该如何滤波的问题。限于篇幅本文仅给出球阀后水压脉动、尾水管进口水压脉动极值分析。

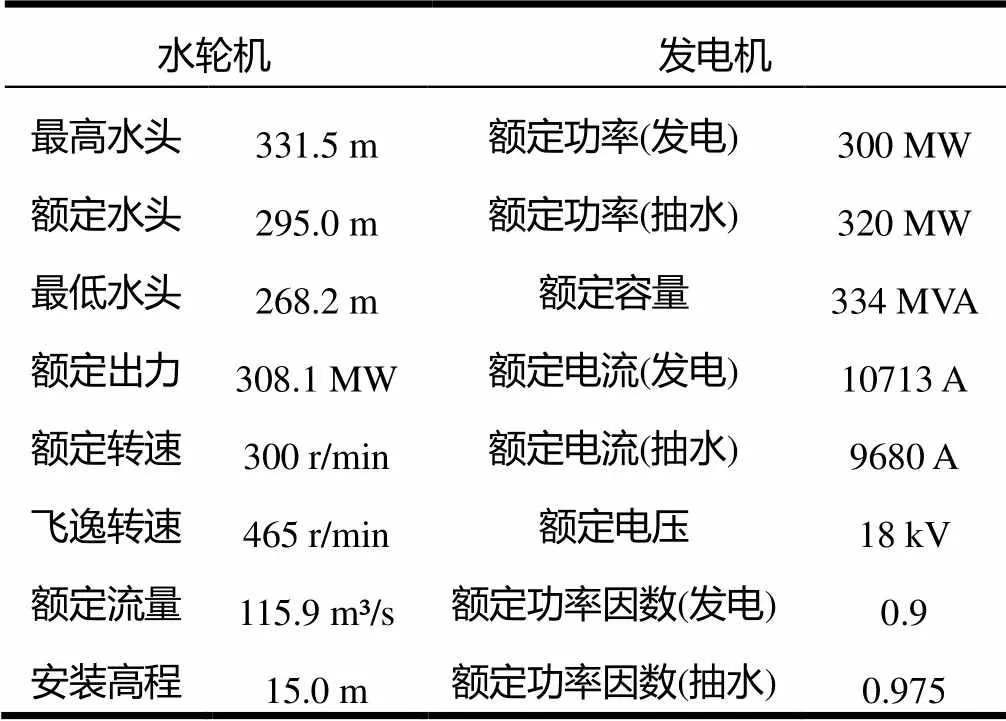
表1 水轮机基本参数

3.2 球阀后水压脉动信号分析

甩100%额定负荷时，上游水位为396.5m，下游水位为78.2m，水头318.30m。甩负荷前导叶接力器行程为74.1%；甩负荷过程中机组频率最大值为68.57 Hz，频率上升率为37.14%。试验过程中采样频率设置为1000Hz，采样时间为470.99s，根据香农采样定律可知，实测的最大信号频率为500Hz。由于水压脉动后期数值降低缓慢，全部显示数据影响极值的观察，故图2仅给出含极值的球阀后水压脉动信号部分截图。从图中可以看出，球阀后水压脉动信号中含有大量“毛刺”，最大值似乎受到“毛刺”干扰，从时域波形中难以确认最值的真实性及有效性。

将本文提出的方法应用于球阀后水压脉动实测数据，分别设置截止频率为100Hz、50Hz、40Hz、30Hz、20Hz、15Hz、10Hz、8Hz、6Hz、4Hz、3Hz。图3~图5给出了分别滤除100Hz、10Hz、3Hz以上频率成分后的球阀后水压脉动信号与原始信号对比图。

从图中可以看出：（1）滤波后时域波形的极值与滤波前的极值发生时刻保持一致，说明在本文提出的方法中相位根本不会发生作用。（2）截止频率越低滤波后的信号极大值越小，滤波后的极小值越大。说明高频成分对极值产生重要影响。

图2 球阀后水压脉动信号原始波形

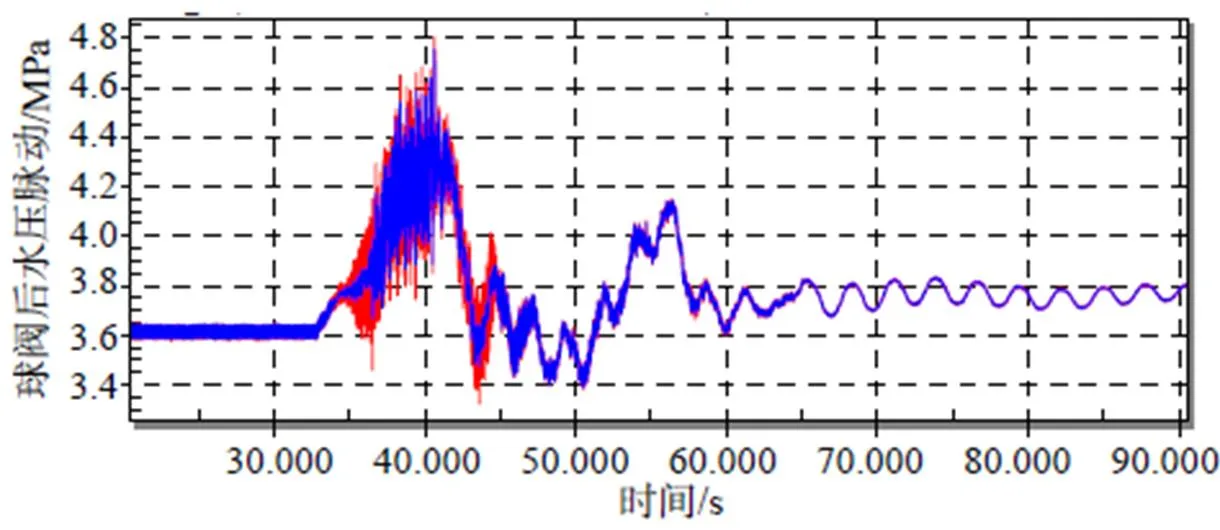
图3 经滑动截止频率滤波后球阀后水压脉动（截止频率fr=100Hz）

图4 经滑动截止频率滤波后球阀后水压脉动（截止频率fr=10Hz）

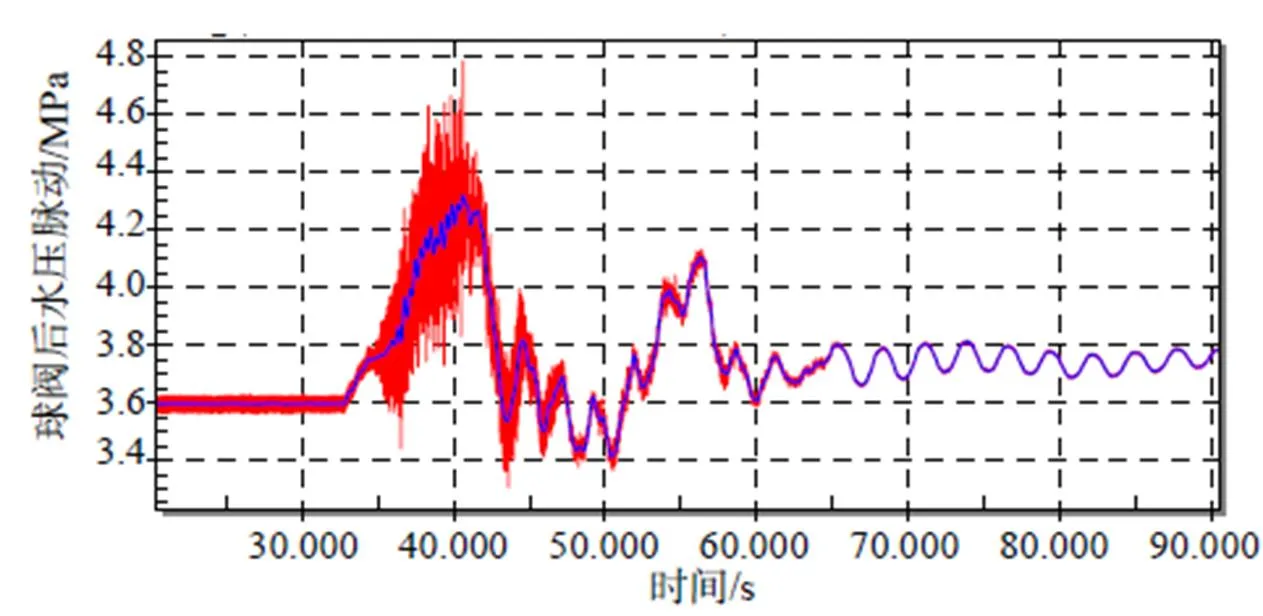
图5 经滑动截止频率滤波后球阀后水压脉动（截止频率fr=3Hz）

图6给出了不同截止频率下球阀后水压脉动极大值变化趋势，从图6中可以看出截止频率为50Hz和100Hz时球阀后水压脉动最大值变化不大，但截止频率从3Hz变化到40Hz时，球阀后水压脉动最大值发生显著变化。

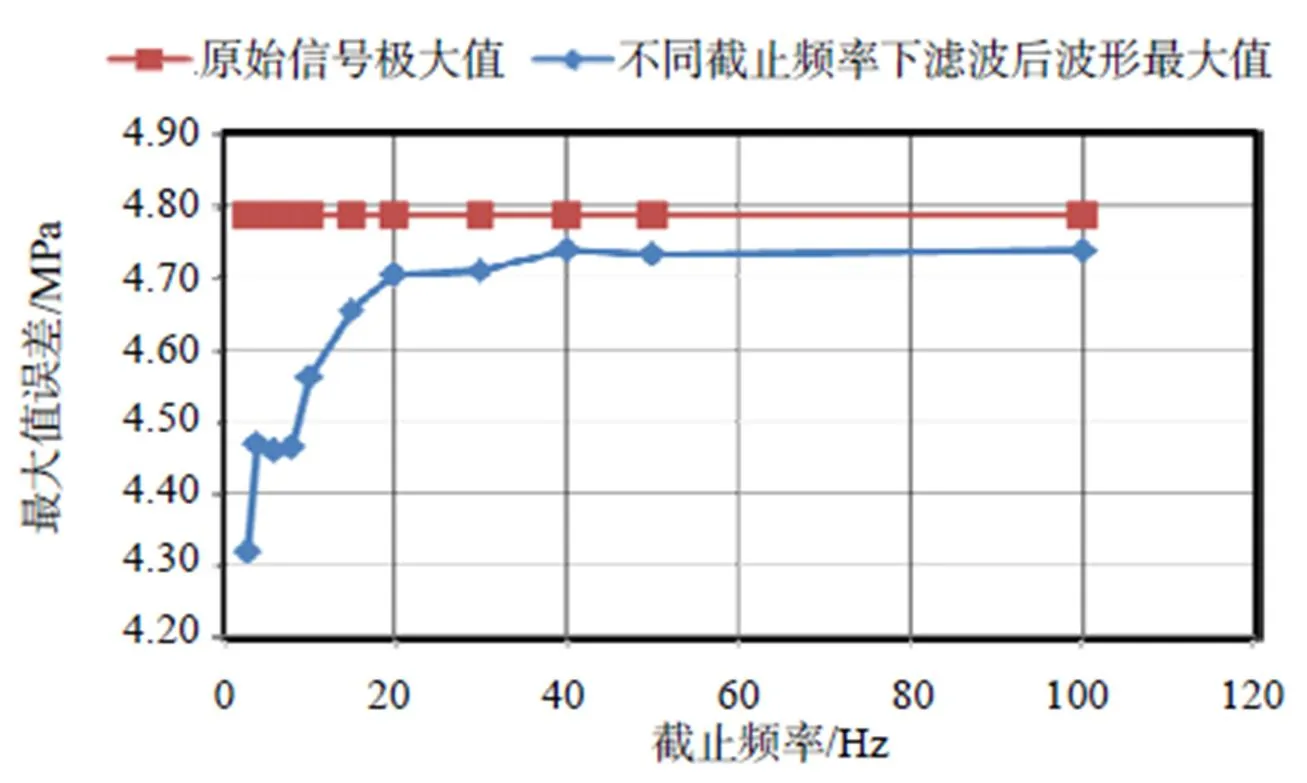
图6 球阀后水压脉动最大值-截止频率关系曲线

图7给出了滤波后信号极大值与原始信号极大值误差曲线随截止频率变化趋势，表2给出了具体的数值。从图中及表中可以看出：（1）随着截止频率大于50Hz后，滤波后信号水压脉动极大值与原始信号极大值间误差逐渐变小，说明50Hz及以上频率成分对水压脉动极大值影响有限，滤除50Hz及以上信号时球阀后水压脉动降低了5.61m，滤除100Hz及以上频率成分时，球阀后水压脉动降低了5.10m，50~100Hz间频率成分对水压脉动的影响仅为0.51m水柱。（2）随着截止频率从50Hz降低到3Hz，滤波后水压脉动信号最大值与原始信号实测值间偏差逐渐增大，由50Hz时的5.61m水柱增大至47.55m水柱。说明滤波的截止频率过低已经严重影响了水压脉动信号最大值的真实性。（3）通过对比表2中不同截止频率对水压脉动极值的影响，截止频率取100Hz时，滤波后水压脉动极大值与实测信号极大值间偏差仅5.10m水柱，约为甩负荷时水头318.30m的1.602%。

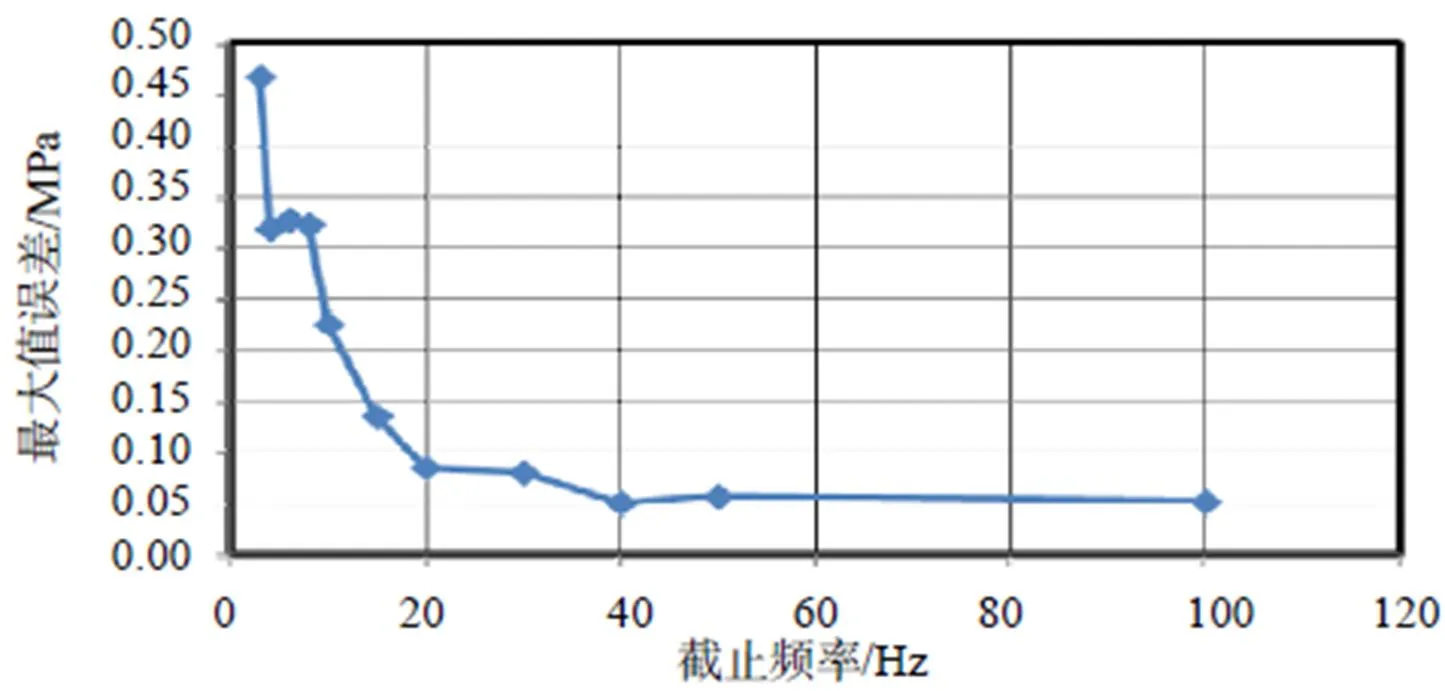
图7 球阀后水压脉动最大值误差-滑动截止频率关系曲线（MPa与水柱之间换算见表2）

3.3 尾水管进口压力脉动信号分析

同样将本文提出的方法应用于尾水管进口压力脉动实测数据，分别设置截止频率为100Hz、50Hz、40Hz、30Hz、20Hz、15Hz、10Hz、8Hz、6Hz、4Hz、3Hz。图8-图11给出了尾水管进口水压脉动原始波形及分别滤除100Hz、10Hz、3Hz以上频率成分后的尾水管进口压力脉动与原始信号对比图。

表2 不同截止频率下球阀后水压脉动极大值与实测信号极大值误差

注：极大值误差=实测信号极大值-滤除截止频率及以上成分的时域波形极大值，表中近似为9.8。

从图中可以看出：（1）滤波后时域波形的极值与滤波前的极值发生时刻保持一致；（2）截止频率越低滤波后的信号极小值越大，滤波后的极大值越小。

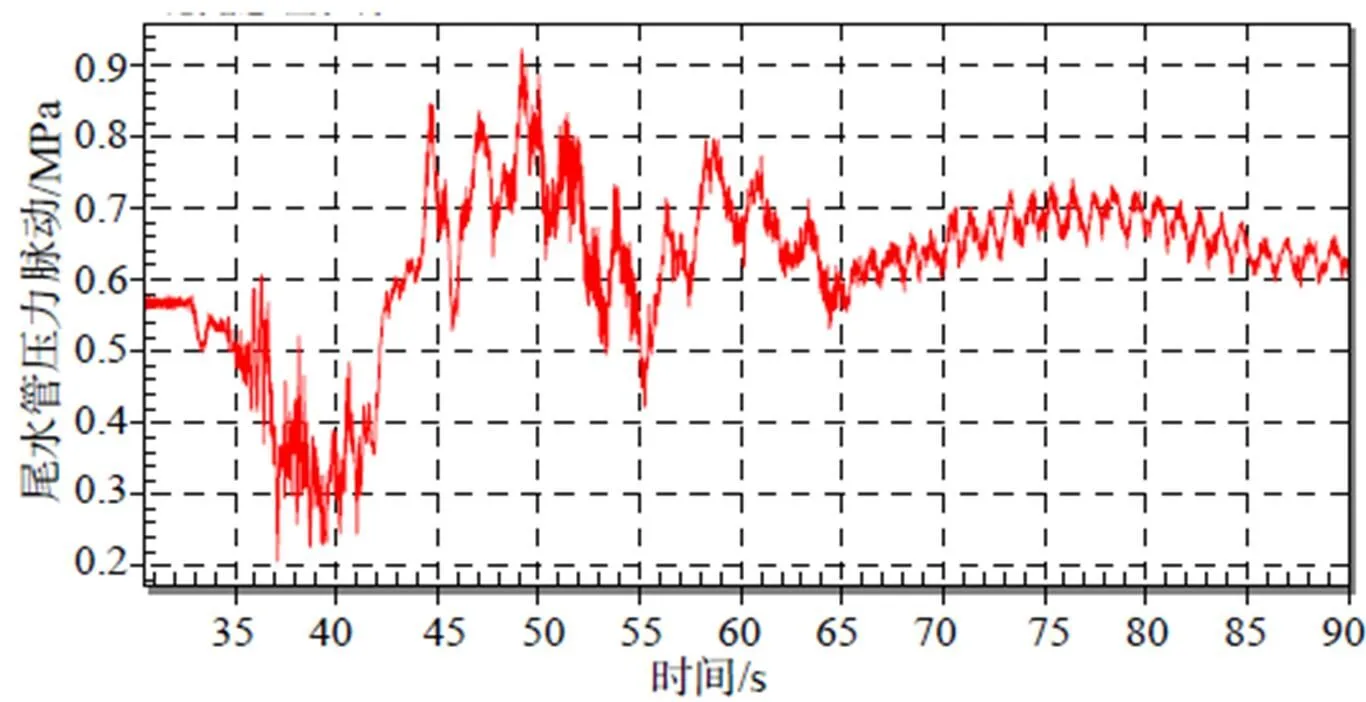
图8 尾水管压力脉动原始波形

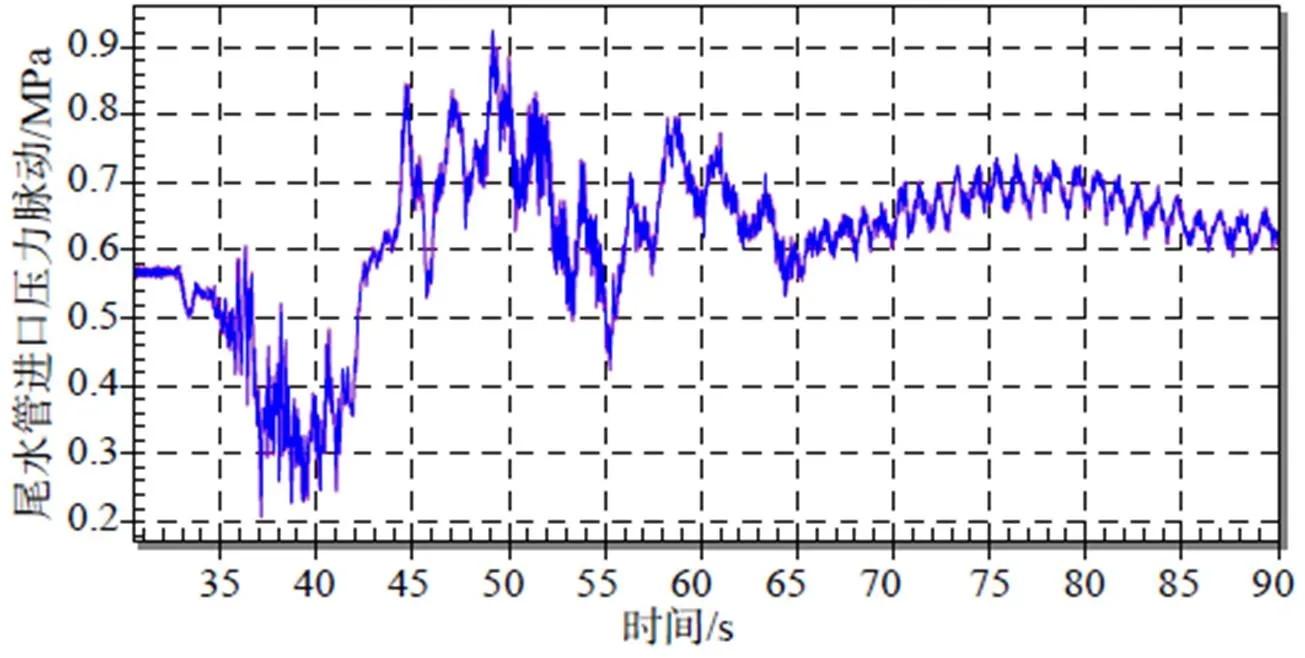
图9 经滑动截止频率滤波后尾水管进口压力脉动（截止频率fr=100Hz）

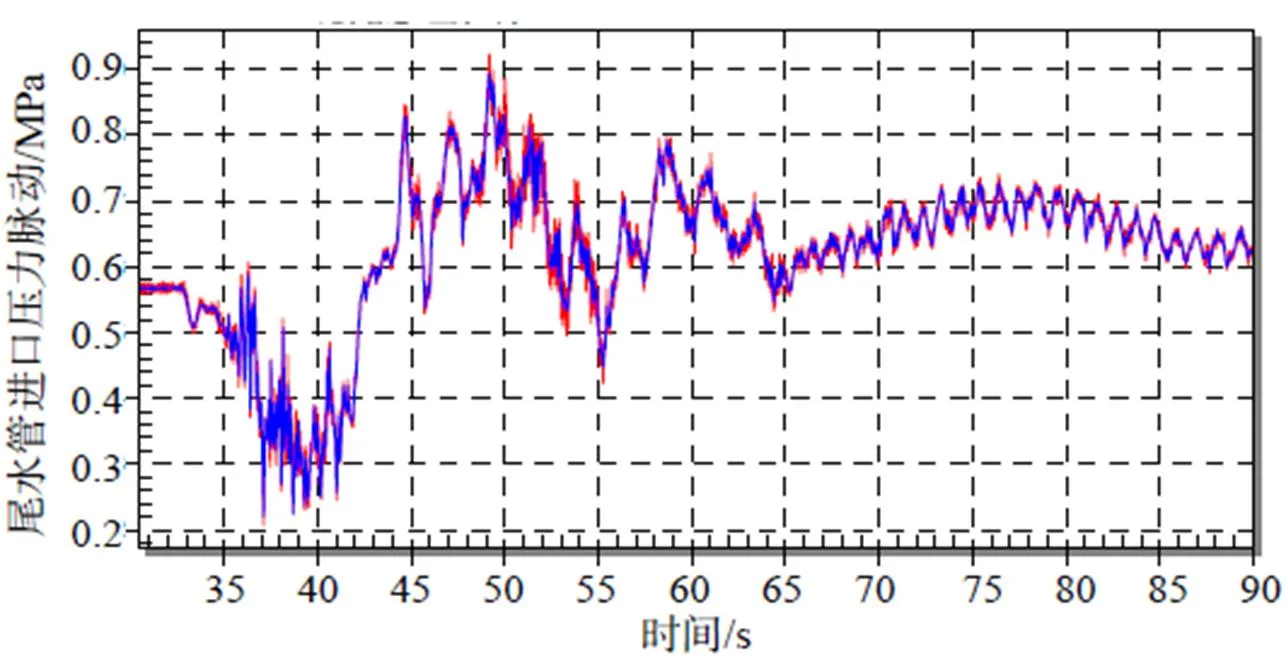
图10 经滑动截止频率滤波后尾水管进口压力脉动（截止频率fr=10Hz）

图11 经滑动截止频率滤波后尾水管进口压力脉动（截止频率fr=3Hz）

图12给出了不同截止频率下尾水管进口压力脉动极小值变化趋势，从图12中可以看出截止频率为100Hz时尾水管进口压力脉动最小值变化不大，但截止频率从3Hz变化到50Hz时，尾水管进口压力脉动最小值发生显著变化。

图13给出了滤波后信号极大值、极小值与原始信号极大值误差曲线随截止频率变化趋势，表3给出了具体的数值。从图中及表中可以看出，（1）50Hz及以上频率成分对尾水管进口水压脉动极值影响有限，滤除50Hz及以上信号时尾水管进口压力脉动极小值增大了0.2m，极大值降低了0.1m。滤除100Hz及以上频率成分时，尾水管进口压力脉动极值未发生变化。（2）随着截止频率从40Hz降低到3Hz，滤波后水压脉动信号最小值与原始信号实测值间偏差逐渐增大，由40Hz时的0.2m水柱增大至5.31m水柱；滤波后水压脉动信号最大值与原始信号实测值间偏差逐渐增大，由40Hz时的0.61m水柱增大至4.39m水柱。说明滤波的截止频率过低已经严重影响了水压脉动信号最大值的真实性。（3）通过对比表2中不同截止频率对水压脉动极值的影响，截止频率取50Hz时，滤波后水压脉动极小值与实测信号极大值间偏差仅0.20m水柱，约为调节保证值-8m的2.5%。

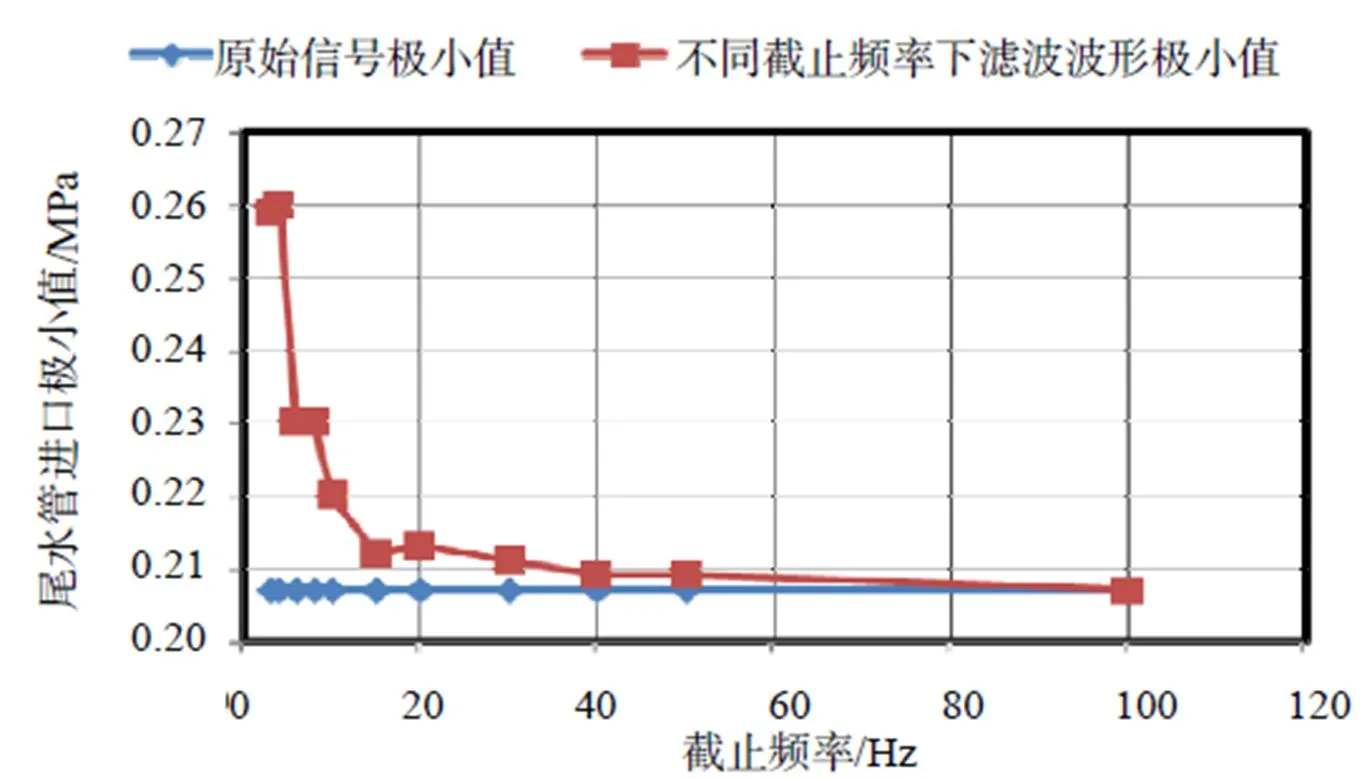
图12 尾水管进口压力脉动最值-滑动截止频率关系曲线

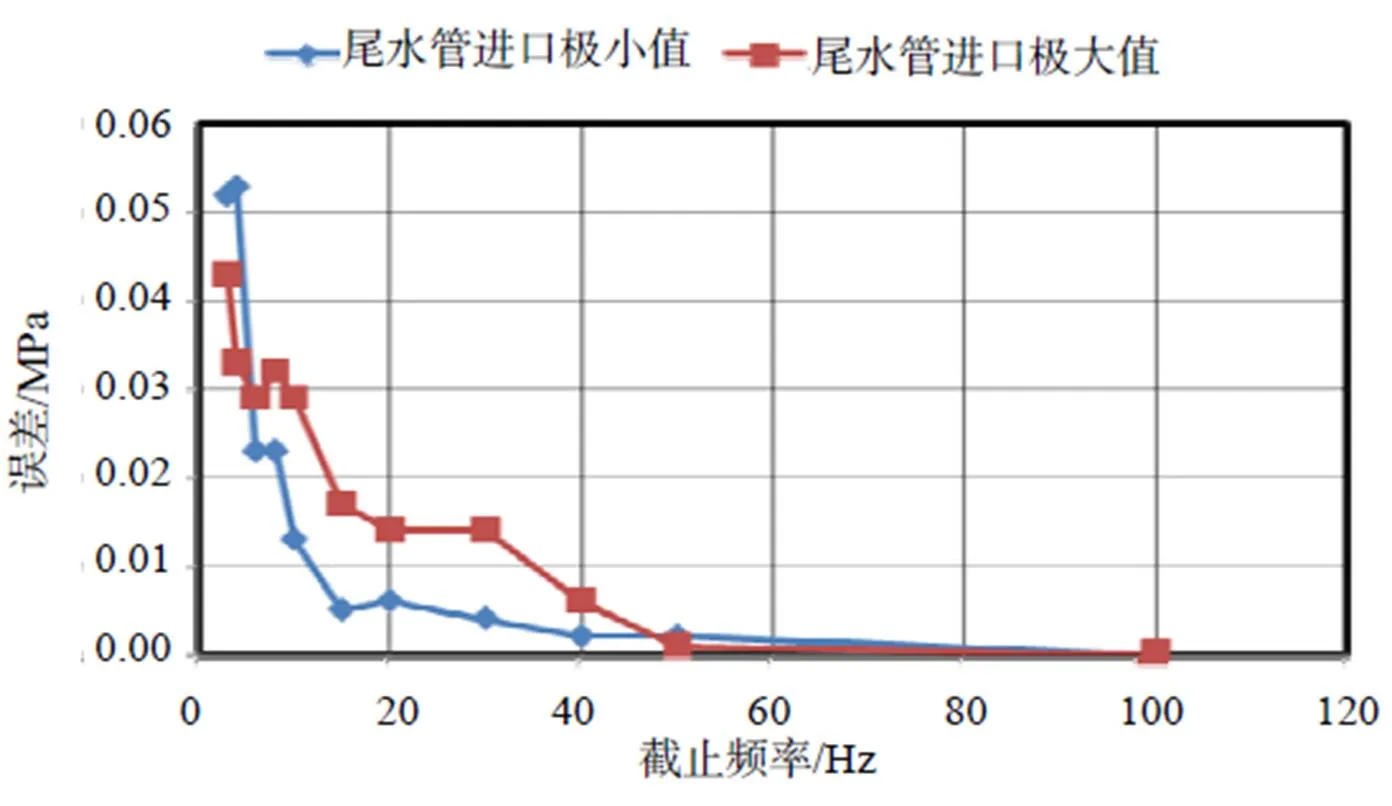
图13 尾水管进口压力脉动最值误差-滑动截止频率关系曲线（注：图中尾水管极小值误差=滤波后波形极小值-原始信号尾水管极小值，图中尾水管极大值误差=原始信号尾水管极小值-滤波后波形极小值）

表3 不同截止频率下极大值与实测信号极大值误差

注：图中尾水管极小值误差=滤波后波形极小值-原始信号尾水管极小值，图中尾水管极大值误差=原始信号尾水管极小值-滤波后波形极小值，表中g近似为9.8。

4 结论

工程实践中水轮发电机组甩负荷过渡过程蜗壳进口水压最大值或球阀前后水压极大值、尾水管进口水压极小值对评价水电站调保计算、电站的安全运行具有重大意义。然而实际测量的水压脉动信号中往往含有大量的“毛刺”及干扰，严重影响实测数据极值真实性的认识与评价。为此，本文基于Fourier变换提出了一种频域分段-时域反演的水压脉动信号分析方法，研究了不同截止频率对抽水蓄能机组甩100%额定负荷后球阀后水压脉动、尾水管进口水压脉动极值的影响，研究所得结论如下：

（1）滤波处理确实会改变实测信号的极值。截止频率取100Hz时，球阀后水压脉动信号滤波后极大值比实测信号极大值降低了5.10m水柱，尾水管进口水压脉动极值未发生变化。

（2）随着截止频率降低，球阀后水压脉动信号滤波后极大值与实测信号极大值相比降低更低，尾水管进口水压脉动极大值与实测信号极大值相比降低更低，尾水管进口水压脉动极小值与实测信号极小值相比增加更大。

（3）低频成分决定了水压脉动的趋势，高频成分对球阀后水压脉动信号极致具有重要贡献作用，建议实际试验时使用实测的原始数据读取水压脉动极值，尽可能不要对实测信号进行滤波处理。

[1] 张进, 冯志鹏, 卢文秀. 交叉小波变换在水轮机非平稳信号分析中的应用[J]. 中国电机工程学报, 2015, 30(23): 84-89.

[2] 林雯婷, 张克危. 小波变换及其在水轮机水压脉动信号处理中的应用[J]. 大电机技术, 2002, (6):47-58.

[3] 韩凤琴, 陈林网, 桂中华. 基于小波包提取尾水管水压脉动特征的研究[J]. 水电能源科学, 2005, 23(1): 31-33.

[4] 冯志鹏, 褚福磊. 基于Hilbert—Huang变换的水轮机非平稳压力脉动信号分析[J]. 中国电机工程学报, 2005, 25(10): 111-115.

[5] 万永革. 数字信号处理的MATLAB实现[M]. 科学出版社, 180-240.

The Pressure Fluctuation Signal Analysis of Pump Hydraulic Turbine Based on Segment in Frequency Domain and Peak Analysis in Time Domain

KOU Pangao1, DENG Lei2, LIU Ping3, WU Changli1

(1. Hunan Electric Power Company Science Research Institute, Changsha 410007, China;2. State Grid Xinyuan Company Technology Center, Beijing 100161,China;3. State Grid XinYuan Hunan Heimifeng Pumped Storage Limited Company, Changsha 410003, China)

During the load rejection process of pumped storage unit, there are many burr in the pressure fluctuation signal. The instantaneous sharp jump serously influences the analysis and selection of maximum or minimum pressure. Focus on the problem, the paper introduced an analysis method named Segment in Frequce Domain and Peak Analysis in Time Domain(SFDPATD). Based on this mehod, the pressure fluctuation signal was firstly carried out Fourier Transform and the spectrum was got. With setted cut-off frequency and inverse Fourier Transform used, the pressure fluction signal was filtered and the pressure fluctuation signal with setted frequency segment was got. With different cut-off frequency setted, the relationship between cut-off frequency and maximum or minimum pressure fluctuation was analized. Then, with the sensitivity analysis of different frequency bands related to the maximum or minimum pressure fluctuation carried out, effect of filtering frequency on pressure pulsation was displayed. With the mehod applied to pressure fluctuaion of pumped storage unit, it provides a powerful argument for the determination of the maximum value of water pressure pulsation.

pumped storage unit; pressure fluctuation signal; ensemble empirical mode decomposition; partly ensemble empirical mode decomposition

TM612, TK734

A

1000-3983(2016)06-0041-07

2015-12-04

寇攀高（1985-），2012年毕业于华中科技大学，现从事水能与动力工程专业，博士，工程师。

审稿人：宫让勤