空间点到直线距离的新算法
陈士龙,邹新民
(1.长江大学 信息与数学学院,湖北 荆州 434023;2.湖北省监利中学,湖北 监利 433300)
空间点到直线距离的新算法
陈士龙1,邹新民2
(1.长江大学信息与数学学院,湖北荆州434023;2.湖北省监利中学,湖北监利433300)
运用极值原理,给出了直线一般方程条件下空间点到直线的距离公式.
平面束;内积;极值;距离
1 问题的提出

2 新算法研究
π:μ(A1x+B1y+C1z+D1)+λ(A2x+B2y+C2z+D2)=0(μλ∈R)的距离d(μ,λ)的最小值和最大值都存在,且最小值dmin=0,最大值dmax=|PQ|(其中PQ⊥直线L,垂足为Q).
证明如图一所示,设经过直线L且与直线PQ垂直的平面为π0,过直线L的平面π与π0夹角为θ(0≤θ≤π/2),则点 P到平面 π的距离 d=|PQ|cosθ,当θ=0、π/2时,得dmax=|PQ|、dmin=0.
μ(A1x+B1y+C1z+D1)+λ(A2x+B2y+C2z+D2)=0(λ∈R),它表示除π2外的经过直线L的所有平面[2],于是由引理1可得:
推论设直线L外一点P(x0,y0,z0)到平面
(A1x+B1y+C1z+D1)+λ(A2x+B2y+C2z+D2)=0的距离为d(λ),PQ⊥直线L,垂足为Q,则:
i)当且仅当P∈π2时,d(λ)有最大值但无最小值;
ii)当且仅当PQ⊥π2时,d(λ)有最小值但无最大值;
iii)除i)、ii)情形外,d(λ)既有最大值又有最小值,且最小值为0,最大值为点P到直线L的距离|PQ|.
定义内积(ni,nj)=AiAj+BiBj+CiCj(i,j=1,2),则点P到直线L的距离:
i)当M2(n1,n2)≠M1(n2,n2)时

ii)当M2(n1,n2)=M1(n2,n2)时

下面来求f(λ)的最大值点:令f'(λ)=0得
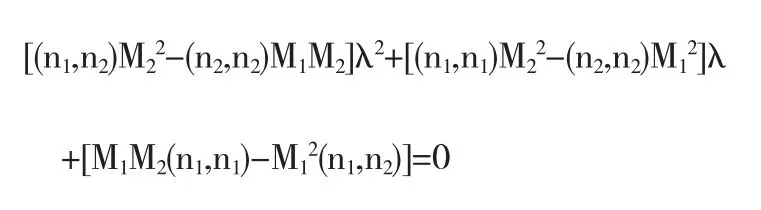
i)当M2(n1,n2)≠M1(n2,n2)时,
10若M2≠0,则(n1,n2)M22-(n2,n2)M1M2≠0,此时f(λ)有两个驻点:
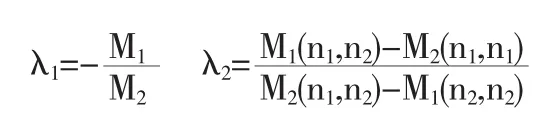
由f(λ1)=0知λ1是f(λ)的最小值点,所以λ=λ2是所求的f(λ)的最大值点,(2)式成立.
20若M2=0(P∈π2,由于P∉L,所以P∉π1,因而M1≠0),则f(λ)仅有一个驻点,此λ即为f(λ)的最大值点(由推论i)知,此时f(λ)无最小值),(2)式成立.
ii)当M2(n1,n2)=M1(n2,n2)时,f(λ)仅有一个驻点
λ*=,且f(λ*)=0,表明f(λ)有最小值但无最大值.
由推论ii)知,此时d等于点P到平面π2的距离:

3 应用举例
解1)用公式(1)求解.
代公式(1)得

2)用定理1求解.
M1=1,M2=5,(n1,n1)=3,(n1,n2)=0,(n2,n2)=6,由(2)式得,于是

4 结束语
本文给出的计算方法具有程序化特点,容易推广到n维空间内点到两超平面交线的距离的情形.
O13
A
1673-260X(2016)07-0010-02
2016-03-13
〔1〕江苏师范学院数学系.解析几何[M].北京:高等教育出版社,1984.
〔2〕同济大学应用数学系.高等数学[M].北京:高等教育出版社,2002.

