基于ARIMA模型的安徽省城镇化水平预测研究
王巍
(池州学院,安徽 池州 247000)
基于ARIMA模型的安徽省城镇化水平预测研究
王巍
(池州学院,安徽池州247000)
城镇化发展水平同一个地区经济发展水平、政府政策制定与实施密切相关.运用时间序列理论,以ARIMA模型为重要分析工具,选取安徽省1955-2014年城镇化水平数据,利用EViews软件拟合了ARIMA模型并对未来安徽省城镇化水平进行了短期预测.结果表明,ARIMA(1,2,1)模型通过了参数显著性检验和模型显著性检验,模型的拟合效果良好,并且安徽省城镇化水平短期预测精度高.模型预测结果表明,安徽省未来城镇化发展势头较好.
时间序列;ARIMA模型;城镇化水平;预测
城镇化水平是衡量一个地区经济发展水平的重要标志,也是考察一个地区城镇化进程的基本方法.所谓城镇化是指农村人口不断向城镇转移,第二、三产业不断向城镇聚集,从而使城镇数量增加,城镇规模扩大的一种历史过程.城镇化的核心是人口就业结构、经济产业结构的转化过程和城乡空间社区结构的变迁过程.因此,为了反映人口在城镇的集中过程和程度,城镇化水平一般用城镇人口占总人口的百分比来表示.
对于城镇化水平的研究,关于城镇化速度的预测,近年来已经形成了诸多预测方法,主要有:(1)新陈代谢GM(1,2)模型预测法.白先春,李炳俊(2006)采用新陈代谢GM(1,1)进行了预测,很好的实现了灰色系统新信息优先的原理,但是没有充分开发利用已知的“最少”信息;(2)趋势外推预测法.常用的趋势外推预测模型有多项式模型、指数模型、修正指数模型、幂函数模型、逻辑斯蒂模型(Logistic)和龚伯茨模型等.李迅等(2000)用1980-1998年我国城镇化水平数据以时间t为自变量,城镇非农业人口比重Yt为因变量,拟合了一次多项式模型;(3)经济因素相关分析预测法.城镇化与经济发展相互影响,经济发展促进人口向城市流动,提高城镇化水平.周一星(1982),李文溥、陈永杰(2001)选取了人均GNP的对数值作为自变量,构造了半对数回归模型;饶会林(1999)选取了工业劳动人口比重,构造了简单线性回归模型;李迅等(2000),王金营(2003)选取了人均GDP分别构造了回归模型.
本文利用城镇化水平的时间序列数据建立ARIMA模型对安徽省城镇化水平进行分析和预测.结果表明:应用ARIMA(p,d,q)模型拟合安徽省城镇化水平的短期数据精确度很高,预测结果对安徽省城镇化水平发展趋势的判断具有一定的指导意义.
1 时间序列ARIMA模型
1.1ARIMA模型的结构
ARIMA模型又称之为求和自回归移动平均模型,简记为ARIMA(p,d,q),具有如下结构:

式中,▽d=(1-B)d;Φ(B)=1-ø1B-…-øpBp为平稳可逆序列模型的自回归系数多项式;Θ(B)=1-θ1B-…-θqBq为平稳可逆序列ATMA(p,q)模型的移动平滑系数多项式.
求和自回归移动平均模型这个名字的由来是因为d阶差分后序列可以表示为:

式(1.1)可以简记为:

由式(1.2)可以看出,ARIMA模型的实质就是差分运算与ARIMA模型的组合,即任何非平稳序列都可以通过差分运算实现平稳后再建立ARMA模型了.
1.2时间序列的平稳性检验
序列满足平稳性条件是建立模型的首要前提,建模之前首先要对序列进行平稳性检验.平稳性检验的方法主要有时序图检验、自相关图检验以及单位根检验.鉴于时序图检验和自相关图检验较大程度上受到人的主观因素的影响,这里采用单位根检验法.而ADF检验是单位根检验中最常见的.以AR(p)过程为例,其特征方程为:
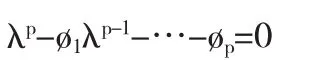
若特征方程的所有单位根都在单位圆内,则序列满足平稳性条件.构造ADF检验统计量如下:
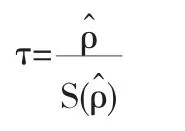
1.3模型定阶
模型定阶主要依据样本的自相关系数和偏自相关系数,根据它们表现出来的性质,选择适当的模型拟合观察值序列.即根据样本观测值序列的自相关系数和偏自相关系数的性质估计自相关阶数p和移动平均阶数q.模型的定阶过程也就是模型的识别过程.模型定阶的基本原则如表1所示.

表1 ARMA模型定阶
相关系数截尾及阶数的判断很大程度上依靠人的主观经验,但样本自相关系数和偏自相关系数的近似分布对模型的定阶具有很大的帮助.通常,若样本自相关系数或偏自相关系数在最初的d阶明显超出2倍标准差,而后几乎95%的自相关系数都落在2倍标准差范围内,且衰减为小值的过程非常突然,这种情况视为自相关截尾,阶数为d.反之,视为拖尾.
1.4模型参数估计与检验
1.4.1参数估计
选择合适的模型后,接着要利用搜集到的序列观察值估计模型中的未知参数.对于一个非中心化的ARMA(p,q)模型,有
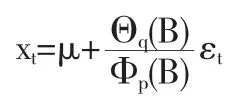
该模型共含有p+q+2个未知参数,未知参数的估计方法主要有三种:矩估计法、极大似然估计和最小二乘估计.
1.4.2模型检验
模型检验主要包括模型的显著性检验和参数的显著性检验.模型的显著性检验主要检验模型提取的信息是否充分,模型是否有效.一个好的拟合模型应能够提取观察值序列中的几乎所有信息,换言之,拟合残差将不再蕴含任何相关信息.因此,模型的显著性检验主要检验残差序列是否是白噪声序列.模型参数显著性检验的目的是为了使模型最为精简,若某个参数不显著,表示该参数所对应的自变量对因变量的影响不明显,该自变量即可剔除.
1.5模型预测
对任意一个未来时刻t+l,∀l≥1而言,该时刻的序列值可以用它的历史数据xt+l+1,…,xt+1,xt,…的线性函数来表示.根据线性函数的可加性,所有的未知历史信息xt+l-1,…,xt+1都可以用已知历史信息xt,xt-1,…的线性函数表示,并用该函数形式估计xt+l,即序列的第l步预测值)为:
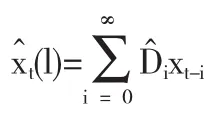
目前,最常用的预测原则是预测方差最小原则,即

2 安徽省城镇化水平预测
通过查询《安徽省统计年鉴(2015年)》得到1955年至2014年安徽省60年的城镇化水平数据,见表2.

表2 1955至2014年安徽省城镇化水平
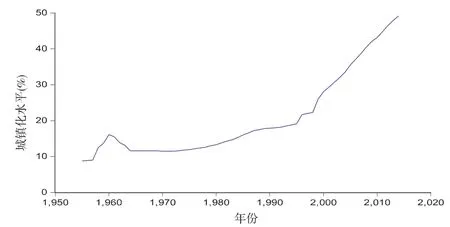
图1 安徽省城镇化变化情况(1955年-2014年)
从图1可以看出,安徽省城镇化水平一直保持增长的态势,尤其是1996之后增长速度明显加快.很明显,安徽省城镇化水平序列不满足平稳性条件,通过差分运算发现,序列的二阶差分序列平稳性较好,并通过了单位根检验,如表3所示.

表3 2阶差分的ADF检验结果
二阶差分序列的自相关偏自相关系数如图2所示,从图可以看出,二阶差分序列自相关系数和偏自相关系数均一阶截尾,因此,原始序列可以建立ARIMA(1,2,1)模型.

图2 2阶差分序列相关系数图
模型参数估计结果如表4所示,从表4可以看出,C、AR(1)、MA(1)的参数均具有显著性,即模型通过了参数显著性检验.

表4 模型参数估计结果
再检验模型的显著性,即检验ARIMA(1,2,1)模型残差序列是否为白噪声序列,见图3.从图中可以看出,各阶延迟下的LB统计量的P值都显著大于0.05,可以认为这个拟合模型的残差序列属于白噪声序列,说明模型已经提取观察值序列中几乎所有的样本相关信息,拟合残差项中将不再蕴含任何相关信息,即拟合模型显著有效.

图3 模型残差项的Q值检验
运用ARIMA(1,2,1)模型对安徽省城镇化水平进行预测,预测结果如表5所示.其中,通过网络查询得知,2015年安徽省城镇化水平实际值为51%,模型预测结果为50.9%,模型的预测值与实际值误差很小,预测误差低于0.2%,说明模型预测效果良好.
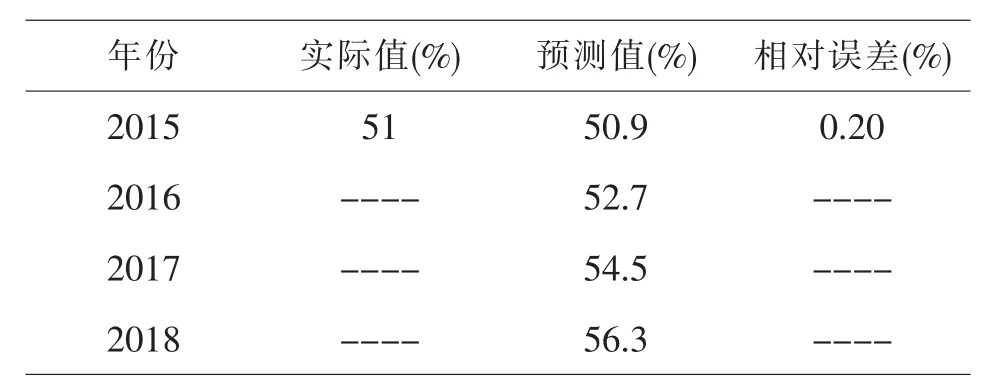
表5 模型预测值与实际值
3 结论
虽然,ARIMA(1,2,1)模型对安徽省城镇化水平预测效果良好,但判别模型的方法和准则很多,只是在某个方面而言模型是最优的.另外,时间序列模型一般适用于短期预测,长期预测误差需要进一步验证,预测效果也待实际检验.安徽省的城镇化水平受到社会、政治、经济、文化等众多要素的影响,城镇化水平发展具有一定程度上偶然性,从长期来看,安徽省城镇化水平表现出增长的趋势.因此,采用ARIMA(1,2,1)模型对安徽省城镇化水平进行短期预测具有一定的参考价值.
〔1〕马军.城镇化水平的度量、评价和预测[J].浙江统计,1999(2).
〔2〕王燕.应用时间序列分析 [M].中国人民大学出版社,2015.135-152
〔3〕张晓峒.EViews使用指南与案例[M].机械工业出版社,2007.232-243.
〔4〕陈夫凯.运用ARIMA模型的我国城镇化水平预测[J].重庆理工大学学报,2014(4).
O21;F224.7
A
1673-260X(2016)07-0015-03
2016-04-12
校级课题2015年池州学院自然科学研究项目:基于地区差异视角的安徽省人口老龄化计量研究(2015ZR004)

