函数极限的几种特殊求法
苏丽
(大连科技学院 基础部,辽宁 大连 116052)
函数极限的几种特殊求法
苏丽
(大连科技学院基础部,辽宁大连116052)
极限是贯穿数学分析全过程的重要概念,极限理论是研究连续、导数、积分、级数的基本工具,然而求解函数极限的方法很多,需要根据函数表达式具体存在的特点选择恰当的方法,使得求解的过程更简单.
极限;洛必达;两边夹法则;泰勒公式;定积分
高等数学的教学过程中,函数极限是其重要组成部分,由于类型比较广泛,复杂涉及连续性,有界性,无穷小量等,所以在求解函数极限的过程中要全面考察函数的状态,力求灵活运用方法,本文总结了几种在高数的教学过程中常用求函数极限的方法.
(1)用洛必达法则结合无穷小等价替换;
(2)幂指函数变形;
(3)用两边夹准则;
(4)用泰勒公式.
(5)定积分求解
下面就函数f(x)的形式给出其求法.
例1求函数的极限



2当f(x)为幂指函数[φ(x)]ψ(x)型的不定型时,可以采用取对数后再求,但为1∞型时亦可用求之.
例2求极限

分析:(1)此题为1∞型,可考虑利用已知极限


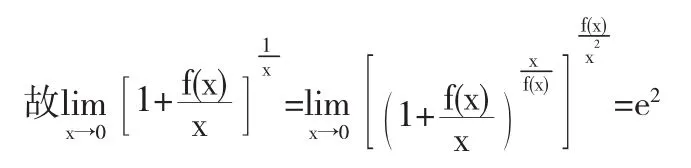
分析(2)此题是1∞型极限,应用已知极限比较麻烦,可考虑先取对数后再求之.或者可以通过泰勒

3当f(x)为不定型时,可考虑用两边夹法则.
分析(1)由于f(x)为不定型,形式不定但与ai有关,因此不能用洛必达法则,又因为表达式中ai为有限项,必有最大值和最小值,因此想到应用两边夹法则.
解令k=max{a1,a2,…,an}

分析(2)因为当x→0+时不确定,所以只能考虑用两边夹法则.
4当函数f(x)表达式为和式,可考虑应用定积分
例4求


5当已知条件中提及级数,可考虑利用级数收敛求极限
以下几个题目感兴趣的同学可以作为练习.

求解极限的方法有很多种,我相信仍在不断的更新,每种方法的产生都源于多样的表达式,所以在求解的过程中应该注重观察特点,找到适合的方法,使得计算简便.
O172
A
1673-260X(2016)07-0008-02
2016-03-21
〔1〕刘玉琏,数学分析讲义[M].北京:高等教育出版社,1988.
〔2〕同济大学应用数学.高等数学[M].上海:同济大学出版社,2004.

