特征加权优化软子空间聚类算法比传统算法的优越性分析

陈晓洁，王雯娟

（龙岩学院　信息工程学院，福建　龙岩　364012）

特征加权优化软子空间聚类算法比传统算法的优越性分析

陈晓洁，王雯娟

（龙岩学院信息工程学院，福建龙岩364012）

聚类算法在当前的各个领域都有着非常广泛的应用，常见的有生物学和医学领域的数据探测、信息检索以及文本挖掘和图像处理等.尤其是目前随着计算机信息技术的发展，数据的规模比以往更大，数据挖掘工作需要的数据特征维数大大增加.导致高维数特征加权和选择面临多学科交叉的问题，大大增加了空间聚类分析的工作难度.本文将分析特征加权优化软子空间聚类算法，并将其与传统算法进行了对比，总结了其优越性.

特征加权；优化软子空间；聚类算法；传统算法

随着信息技术的快速发展，人们在日常的工作过程中，能够更加方便和快捷的采集到数据资源，这就使得数据集群更加庞大和复杂.高维数据比低维数据在空间中存在很多不相关的属性，并具有明显的维度效应.利用聚类分析算法，能够提高数据内部结构的识别能力，发现不同区域的疏密度，从而确定空间的分布模式和数据关系.在计算机以及人工智能领域，该算法模式逐渐成为人们研究对象，为各个领域的相关工作提供了极大的便利性.但是随着目前数据规模的不断扩大以及数据特征的多样性明显增强，在数据挖掘的过程中，不仅需要依赖统计学、计算机以及数学模型等，还得了解生物学、医学和经济学等相关的学科背景.在传统的聚类分析算法中，存在着较大的缺陷型，尤其是在如何自动确定数据集的簇数、高维数据集的特征相似度等方面.但是鉴于聚类算法在各个领域的广泛应用，为了提高空间聚类分析的质量，需要对传统的算法进行改进.经过近几年的研究，针对高维数据提出了很多聚类分析方法，本文主要介绍最具代表性的子空间聚类算法.

1　聚类分析过程及要求

聚类分析的过程为：做好分析数据的准备工作——筛选出有效特征，并将此特征存在矢量中——将数据的特征提取出来——选择合理的距离函数，并利用此函数对特征进行聚类——对聚类结果进行评价、测试.

在不同的应用领域中，对聚类分析的要求也有所差异.不过总体来说，聚类分析过程应该要满足以下要求：第一，所选用的聚类空间算法必须有良好的伸缩性，也就是说能够根据计算要求以及数据特点进行扩展或收缩；第二，对于不同的数据类型，要有相应的处理能力，才能很好地完成不同种数据的聚类分析；第三，由于单个的簇形状并不固定，因此首先要提出能够识别不同形状簇的聚类算法，才能实现有效聚类；第四，如果在数据的录入过程中，出现了人为操作不良而导致的失误，或者数据出现异常，聚类算法要对噪声数据进行及时的处理；第五，在聚类过程中，由于需要输入很多的信息参数，占据很大一部分空间，所以要选择输入参数的领域知识最小的聚类算法；第六，鉴于传统的聚类算法不能在高维度空间中聚类数据对象，要对算法进行改进，从而找到更加高效的聚类算法；第七，在实际应用过程中，聚类算法会受到不同程度的约束条件，为了保证计算过程中的顺利性，需要找到基于约束的聚类算法；第八，通过聚类算法获得的聚类结果必须具备可解释性、可用性以及可理解性［1］.

2　软子空间与硬子空间聚类算法的对比

子空间聚类算法是指在高维数据空间中挖掘存在于某些低维子空间中簇类的技术.利用该方法能够把集群数据划分成多个簇类，然后从中找到集群数据中每个簇类相对应的子空间.根据维度属性的不同，每个簇类都能赋予其相应的权值，权值主要表示和簇类之间的相关程度.在以往的研究过程中，将子空间聚类方法分成了两种基本类型，包括硬子空间聚类和软子空间聚类［2］.其中，硬子空间聚类方法在聚类过程中能够赋予簇类不同维度属性的权值系数是0和1，分别表示属性和簇类的相关度.软子空间聚类和硬子空间聚类的最大区别在于，在聚类过程中能够赋予簇类各维度属性更多权值，权值范围是［0，1］.这样一来，软子空间聚类一方面反映了属性和簇是否具备相关性，另一方面也明确了各自的相关程度.因为两种子空间聚类算法的这一差别，软子空间聚类算法成为近年来数据挖掘领域非常重要的研究对象.但是，很多新的软子空间聚类算法仍然具有较大的局限性，因为它们主要是针对数据集群的划分方法进行的优化，而忽略了各簇类所在子空间的优化，这就大大降低了数据计算的效率以及聚类的精确性.本文提出一种基于特征加权优化的软子空间聚类算法，简称SCFO算法，应用对象是高维数据的聚类分析.该算法的应用优势为：在聚类过程中，不仅实现了数据集群的连续划分，还能完成不同簇类子空间的优化.除此之外，用户除了需要输入簇类数之外，不用再输入其它的参数.经过大量的应用实践证明，该聚类算法具有更好的聚类效果［3］.

3　特征加权优化软子空间聚类算法的优越性分析

3.1FSC算法

与传统的聚类方法相比，软子空间聚类法充分考虑了属性和簇类的相关性，在聚类过程中，会给簇类张每个维度属性一个权值，这些权值各不相同，每一个都代表着一种与簇类的相关性.利用软子空间聚类算法，就能够利用特征权值来识别每个子空间中的簇类［4］.

首先对全文使用符号含义进行说明：

DB=｛x1，…，x1，…，xN｝表示数据集；

V=｛xkj｝C×D表示簇类中心矩阵；

U=｛uki｝C×N表示隶属度矩阵；

W=｛wkj｝C×D表示权值矩阵；

其中，C表示簇组数，D表示数据集中样本点的维数，xij表示样本xi的第j维属性值（j=1，2，…，D），vkj是第k个簇中心点的第j维属性值，uki表示第i个样本对第k类簇的隶属度，wkj表示第j维属性和第k个簇类之间的相关程度，其中，当wkj的值更大时，表示两者之间的相关性更强.

有研究学者提出了一种新的聚类算法FSC，这种算法多应用在高维度的数据聚类处理中.FSC给模糊权值进行定义，并将模糊权值带入到函数中去，得到以下目标函数：

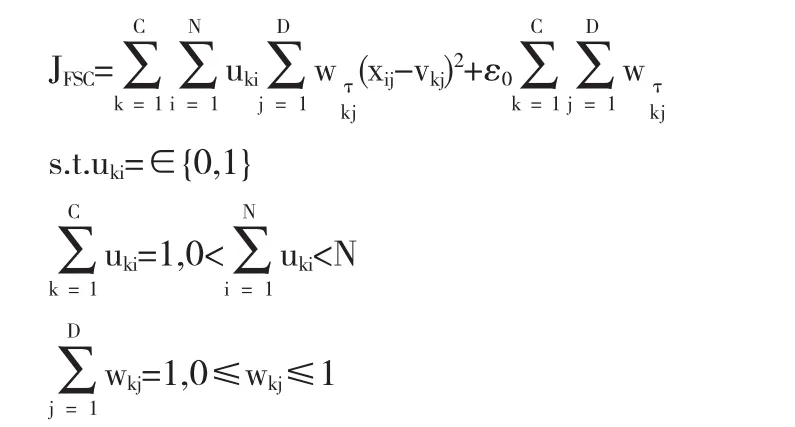
在上述公式中，引入ε0的作用是防止FSC算法在聚类过程中会出现除以零的错误，τ表示模糊因子.FSC算法的模糊权值更新方式和模糊K-均值聚类算法的模糊隶属度的加权方法类似.除此之外，在同一簇类中，赋予每一维属性的权值和该属性上的数据分散程度呈反比，也就是说，数据越分散，被赋予的权值就越小，数据越集中，被赋予的权值就越大.FSC算法首先对簇中心进行初始化，然后连续更新权值矩阵W和聚类中心矩阵V，等到满足条件之后，就会自动结束.软子空间聚类算法就是在FSC算法的基础上研究出来［5］.

3.2特征加权优化软子空间聚类算法

3.2.1目标优化函数

在软子空间聚类算法之中，特征加权有以下特点：在同一个簇类中，权值与其所属维度的数据分散程度是反比例关系，这就说明当维度属性权值越大时，对簇类的重要性就越强.也就是说，特征权值的分布越是集中，就越能体现簇类所在的子空间越优化.当wk1+wk2+…+wkD=1时，可以用以下公式来分析权值的分布情况：

分析上述公式可以发现，特征权值的分布越是均匀，fw和dk的值数就越小.跟一般的传统聚类算法相似的是，当各个属性和簇类的重要程度一样时，fw和dk能够获得最小值.根据公式（1），可以得到以下目标函数：

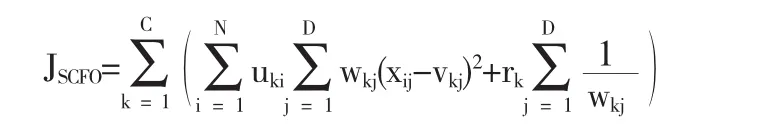
其中，目标函数的第1项是加权的簇内紧凑度之和；系数rk的作用是平衡簇内的紧凑度以及特征权值分布对目标函数的具体影响.

3.2.2特征加权优化软子空间聚类算法算法过程及分析

具体算法描述如下：

输入：簇类个数C；然后随机选择C个初始聚类中心，然后把所有的特征权值的初始值都设置为1/D.

重复：根据上述公式，更新隶属度矩阵U，簇类中心矩阵V，权值矩阵W.

算法结束：直到目标函数值达到最下值或者V和W这两个参数在计算过程中相邻两次的变化比给定的阙值小.输出：将聚类中心矩阵V以及隶属度矩阵U输出.

特征加权优化软子空间聚类算法采用了和k-均值聚类相似的算法，将计算权值特征的具体步骤增加到聚类过程中，还重新定义了每个计算步骤使用的公式.也就是说，该算法极大了保留了k-均值聚类算法的特性.假如要进行P次的循环迭代才能够满足S软子空间聚类算法的结束条件，那么每个步骤都能够获得算法的时间复杂度都是0.由此可以证明，该算法和k-均值聚类算法在计算时间上的复杂性一样［6］.

4　结论

子空间聚类算法其实就是传统的聚类算法与特征选择技术的结合，在进行聚类划分时，得到了与各个数据簇相对应的特征子集，也可以称作是特征权重.这样一来，就能为各个数据簇找到相对应的特征子空间.其中，利用子空间的聚类技术能够根据数据集子空间的不同，找到与之对应的数据簇.由于子空间聚类算法又可以分为硬子空间聚类和软子空间聚类，经过实践表明，软子空间聚类算法的实用性更强.但是传统的软子空间聚类算法具有较大的缺陷型，因此，本文对其进行了优化，基于特征加权优化软子空间聚类算法比传统算法有更大的优越性，不仅能够在聚类过程中对数据集群划分，还可以优化各个簇类的子空间，从而获得更加良好的聚类质量.

〔1〕朱林，雷景生，毕忠勤，杨杰.一种基于数据流的软子空间聚类算法［J］.软件学报，2013（11）：2611.

〔2〕庄景晖.特征加权优化软子空间聚类算法［J］.长春工业大学学报，2015，30（04）：415.

〔3〕邱云飞，杨倩，唐晓亮.基于粒子群优化的软子空间聚类算法［J］.模式识别与人工智能，2015，28（10）:904.

〔4〕毕志升，王甲海，印鉴.基于差分演化算法的软子空间聚类［J］.计算机学报，2012，35（10）:2115.

〔5〕陈黎飞，郭躬德，姜青山.自适应的软子空间聚类算法［J］.软件学报，2010，21（10）:2115.

〔6〕邓文韬.基于几何特征加权和选择的数据空间聚类算法研究［J］.信息技术与信息化，2014（12）：68.

TP311

A

1673-260X（2016）07-0018-02

2016-03-08

龙岩学院青年攀登项目（LQ2014001）；龙岩学院校立服务海西项目（LQ2013009）