改进Schnerr-Sauer模型在水翼空化模拟中的评估分析

洪锋，袁建平，周帮伦，石洋

（1.江苏大学流体机体机械工程技术研究中心，江苏镇江212013；2.埃因霍分理工大学机械工程系，埃因霍分5612AZ荷兰）

改进Schnerr-Sauer模型在水翼空化模拟中的评估分析

洪锋1，2，袁建平1，周帮伦1，石洋1

（1.江苏大学流体机体机械工程技术研究中心，江苏镇江212013；2.埃因霍分理工大学机械工程系，埃因霍分5612AZ荷兰）

为了提高Schnerr-Sauer模型模拟空化流动的能力，基于Rayleigh-Plesset方程和均相流假设建立了一种修正的Schnerr-Sauer空化模型，修正后的模型考虑了湍动能引起的脉动压力和不可凝结气体的影响。联立涡粘度系数修正的SST k-ω湍流模型，对绕二维Clark-Y翼型空化流进行了非定常数值计算，得到了时均化升阻力系数随空化数的变化曲线、云状空化时空泡周期性演变及其水平速度分布规律。通过与已有文献的实验结果对比分析得到，采用修正后的空化模型计算得到的时均化升阻力系数与实验值更为接近，并能较准确地捕捉升阻力系数随空化数的特殊变化规律；修正后的Schnerr-Sauer模型能准确地模拟翼型表面空化云的初生、成长、脱落和溃灭的全过程。本文的研究结果验证了修正后的Schnerr-Sauer模型在水翼空化流数值计算中的可靠性和准确性。

空化流；水翼；空化模型；湍流模型；数值计算；阻力系数；Schnerr-Sauer模型

空化是水动力学中特有的一种物理现象，研究空化现象对改善水力机械和船舰推进器性能具有很现实的工程意义，发展空泡流动的数值模拟技术是目前空化研究领域中的热点［1］。

当前，在工程实际应用中主要使用以下三种类型的空化模型来模拟空化流场:1）基于简化Rayleigh-plesset方程的空化模型（如Singhal等［2］模型、Zwart-Gerber-Belamri［3］模型及 Schnerr-Sauer［4］模型）；2）基于经验得出的比例化空化模型（如Merk-le［5］模型、Kunz［6］模型）；3）通过空泡受力分析得出的空化模型（如Tamura［7］模型）。上述空化模型中，基于简化Rayleigh-Plesset方程的空化模型是在混合多相流模型的不可压缩连续性方程中导出了空化反应速率，由于工程上解决空化问题的需要，ANSYS FLUENT v6.0开始引入Zwart-Gerber-Belamri模型和Schnerr-Sauer模型，并成功模拟了水翼的空化问题［8-12］。然而，文献［13-14］中指出，基于简化Rayleigh-plesset方程的Schnerr-Sauer空化模型在模拟云状空化时存在不足，因此为了改善该类空化模型模拟空化流动的能力，本文基于Schnerr-Sauer模型的思想及均相流假设，推导出一种考虑不可凝结气体及湍流脉动压力影响的修正Schnerr-Sauer模型；然后应用UDF（User-defined Function），把修正后的Schnerr-Sauer模型加载到ANSYS FLUENT v14.5平台并联立涡黏度系数修正的SST k-ω湍流模型对二维Clark-Y翼型的空化流场进行数值计算。通过与原始的Schnerr-Sauer模型模拟结果及已有文献中的实验结果作对比，验证修正后的Schnerr-Sauer模型在非定常空化流动计算中的可行性及准确性。

1　Schnerr-Sauer空化模型改进

参照文献［2］将空化流还原成液态水，空泡及不可凝结气体（non-condensable gas，NCG）的三相混合物，并且重新定义混合流体密度为

式中:αv和ρv分别为空泡体积分数和密度，αg和fg分别为NCG体积分数和质量分数，ρl为液态水的密度。NCG的体积分数与质量分数对应关系为

原始的Schnerr-Sauer空化模型蒸发与凝结项分别为

为了考虑不可凝结气体的影响，将式（3）、（4）修正为

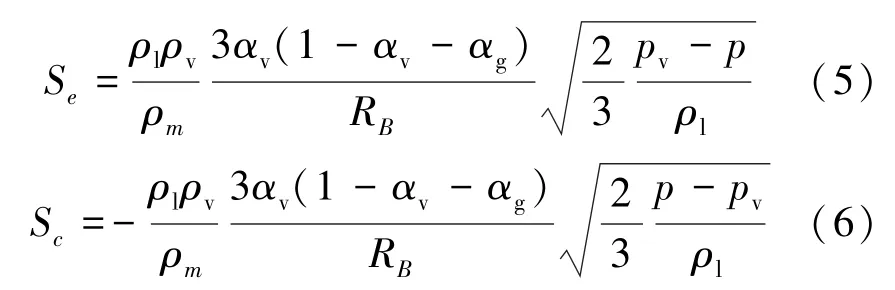
式中:αg为NCG体积分数。为了体现湍流脉动对空话初生的影响，将空化压力进行修正为

式中:pturb为湍动能引起的脉动压力；psat为饱和蒸汽压，取25℃时水的饱和汽化压力psat=3 169 Pa；ρm为混合介质的密度，k为湍动能。

式（5）、（6）就是修正后的Schnerr-Sauer空化模型空化源项，与文献［15］中修正后Schnerr-Sauer模型相比，本文的修正方法还体现了NCG对蒸发及凝结过程的影响。确定不可凝结气体的质量分数和体积分数分别为fg=1×10-6和αg=7.8×10-4。fg直接影响混合密度的改变，进而决定修正粘度μt和pv的改变，从而影响空化初生。αg直接决定空化速率S的改变，进而影响翼型的空化范围［16］。

2　湍流模型及局部可压缩性修正

由于最初的RANS（或URANS）湍流模型是在单相、完全不可压缩介质的基础上发展起来的，因而不能直接应用在可压缩的两相流动数值计算中。在使用RANS模型模拟空化流动时会过渡预测空穴尾部的湍流黏度，导致在空穴尾部区域产生了比实际大很多的粘滞力并阻碍流场中回射流结构因能量不足而无法向上游运动。因此，在使用RANS模型模拟这类空化流场时就无法准确模拟物理现象的本质特征，从而使得模拟失真。为了提高对水翼表面空化的预测精度，根据Reboud等［17］的思想，考虑到气液混合区局部可压缩性的影响，本文采用SST k-ω并对湍流黏度μT作如下相应的修正:

式中:n取值为3，ρm为混合流体密度，k为湍动能，ω为耗散率，其余变量与原始SST k-ω湍流模型保持一致。

3　计算网格及边界条件

计算采用弦长c=70 mm的Clark-Y型水翼，图1给出了计算区域及其边界条件。计算区域的入口距翼型前缘为4c，出口距翼型尾缘的距离为5c。为了保证壁面函数对无量纲y+值的要求，对翼型周围近壁面区域进行了网格加密，如图2所示。

数值计算边界条件为速度进口、压力出口，上下边界均为自由无滑移壁面条件，翼型表面采用绝热、无滑移固壁条件。为了保证与实验条件一致，设定进口速度为Uin=10 m/s，出口压力大小根据空化数取得。翼型攻角α=8°，由弦长、来流速度及介质的黏度系数，得到对应的雷诺数Re=7×105。

图1　计算域及其边界条件Fig.1 Computational domain and boundary conditions

图2　计算网格Fig.2 Computational meshes

本文对计算域划分了4套不同尺寸的网格并作网格无关性验证，网格节点数分别为N1=69 226，N2=83 208，N3=105 588及N4=123 188。网格无关性验证结果如表1所示，从表1中可以看出，当网格数大于N3时，两种不同空化数条件下水翼的升阻力系数相对变化均小于1%，表明此时网格数量对计算结果的影响可以忽略。同时，网格数为N3时，翼型的升阻力系数与试验值误差均在5.5%以内。图3、4分别为当空化数σ=3.0时通过计算得到的翼型表面压力系数（-Cp）及无量纲y+值，从图中可以看出，压力系数计算值与实验值吻合较好且翼型表面网格的y+大部分在30～90，满足壁面函数对近壁面区域网格的要求。因此，最终选择网格3作为本文的计算网格。

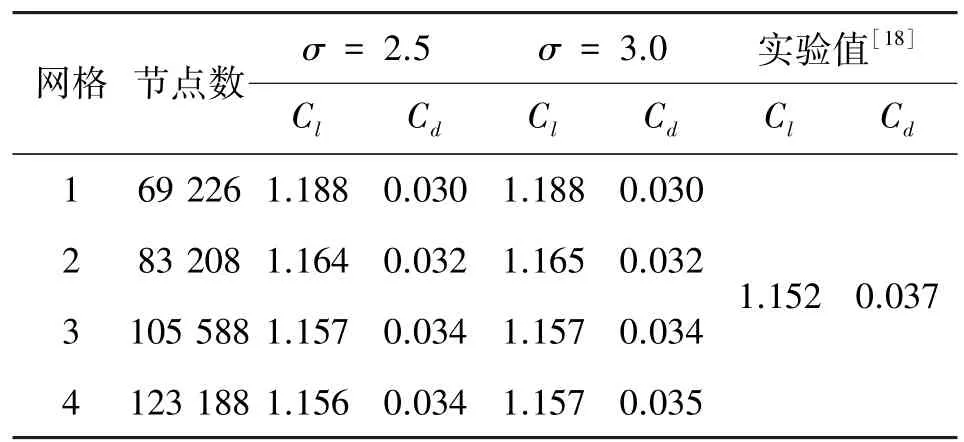
表1　网格无关性验证Table 1 Mesh independence check

图3　水翼表面压力系数分布Fig.3 Surface pressure coefficient of hydrofoil

图4　水翼表面y+分布Fig.4 Wall y+distribution of hydrofoil

4　计算结果及分析

4.1时均化升阻力系数

为研究在不同程度空化条件下，采用修正后的Schnerr-Sauer模型及涡黏度系数修正的SST k-ω湍流模型的联合求解能力。本文通过数值计算的方法得到了原始Schnerr-Sauer模型及修正后的Schnerr-Sauer模型在多种空化数条件下水翼的升阻力系数，并与已有文献中的实验结果作对比分析，结果如图5所示。由于空化是一种包含相变的瞬时物理现象，本文所有计算均为非定常，时间步长设置为Δt= 1×10-4s，总迭代步数设置为2 000，取最后8个周期内升阻力系数的平均值作为时均化后的计算结果。定义空化数σ，升力系数Cl及阻力系数Cd分别为

式中:pout为出口压力，pv为空化压力，ρl为水的密度，Uin为来流速度，c为翼型弦长。

分析升力系数可以看出，在无空化条件下，由于介质中空化核的存在以及不可凝结气体的作用，导致二者计算得到的升力系数并不相同。采用修正后的Schnerr-Sauer模型得到的升力系数与实验值相比略微偏高，而原始Schnerr-Sauer模型模拟得到的计算值比实验值低，如图5（a）所示。根据实验描述［18］，当空化数降低至σ=1.6时，初生空化形成，此时翼型头部的低压区流体因发生空化而形成了典型的游离型泡状结构，并附着于水翼表面，从而导致升力系数出现了小幅上升。从图中可以看到，修正后的Schnerr-Sauer模型能够捕捉到升力系数这种特殊的行为特征，而原始的Schnerr-Sauer模型不具有这种能力。随着空化数降低至σ=1.4时，游离型空泡逐渐过渡到片状空化，此时水翼吸力面附着有一层呈片状的空穴薄层，并最终导致升力急剧下降。

分析阻力系数可以看出，两种空化模型预测得到的阻力系数均低于实验值，在空化初生时，阻力系数才开始迅速增大，但是修正后的Schnerr-Sauer模型模拟得到的阻力系数与实验值变化趋势一致，即在空化数σ=1.6时才开始增大，而原始的Schnerr-Sauer模型在空化数为σ=1.8处时就开始增大；当空化数降低至σ=1.0左右时，云状空化开始逐渐形成，这时阻力系数达到最大值，从图中可以看出，修正后的Schnerr-Sauer模型模拟得到的阻力系数也达到最大值，而原始的Schnerr-Sauer模型计算得到的阻力系数保持继续上升趋势，表明原始的Schnerr-Sauer模型无法捕捉阻力系数在云状空化条件下的这种特殊变化规律。综上，无论是在非空化条件还是空化条件下，修正后的Schnerr-Sauer模型与原始的Schnerr-Sauer模型相比，更能准确地预测翼型所受到的升阻力。

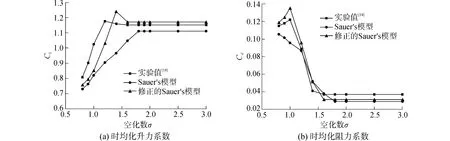
图5　时均化升阻力系数预测值与实验值［18］对比Fig.5 Comparisons of time-averaged lift and drag coefficients between simulation and experiment［18］

4.2准周期性的云状空化

4.2.1云状空化形态演变

当空化数降低至σ=0.8时，附着于翼型表面上片状空穴薄层的长度和厚度都出现了明显增大，靠近尾缘处的空穴形态逐渐变得不稳定并有大量空泡脱落，云状空化形成［16］。采用两种空化模型计算得到的云状空化及实验结果如图6所示，每个分图中左栏为实验结果［19］，右栏上为采用修正后的Schnerr-Sauer模型的模拟结果，右栏下为采用原始的Schnerr-Sauer模型的模拟结果。需要注意的是，根据实验测量，云状空化演化周期为40 ms，采用修正的Schnerr-Sauer模型计算得到的云状空化演化周期为35.9 ms，而原始的Schnerr-Sauer模型计算得到的云状空化演化周期为30.2 ms，表明修正后的Schnerr-Sauer模型预测得到的云空化周期性演变过程与实验结果基本一致。

云状空化一个周期内演化主要分为以下几个阶段:1）在t=t0时刻，翼型前缘处片状空穴几乎消失，尾缘处空泡开始逐渐脱离翼型壁面，从图中可以看到，原始的Schnerr-Sauer模型模拟得到的空穴形态与实验结果相差较大，而修正后的Schnerr-Sauer模型的缺陷是无法模拟出此时翼型前缘处的少许片状空穴，但能较好地模拟尾缘处逐渐脱离翼型表面的空泡团；2）在t=t0+38%T时刻，附着于翼型表面的片状空穴发展至最大长度且尾缘处的空泡团消失，修正后的Schnerr-Sauer模型模拟的空穴长度与实验结果吻合较好，而原始的Schnerr-Sauer模型无法准确模拟此时的片状空穴形态；3）在t=t0+70%T时刻，翼型尾缘处的空泡团逐渐脱落并向下游移动，对比发现，修正后的Schnerr-Sauer模型能够捕捉到尾缘处脱落的空泡，而原始的Schnerr-Sauer模型捕获这一细节的能力欠佳；4）在t=t0+84%T时刻，翼型前缘的片状空穴又开始逐渐回缩，尾缘处的大体积空泡团逐渐形成，开始重复t=t0时刻空泡形态特征。

4.2.2云空化水平速度分布特性

为了揭示云空化流场的运动特性，研究了流场内四个不同位置（x/c=0.4、x/c=0.6、x/c=0.8和x/c=1.2，其中x为水平方向到水翼前缘的距离，y为垂直方向到水翼表面的距离）上的水平速度分布，结果如图7所示。整体上看，与原始的Schnerr-Sauer模型相比，采用修正后的Schnerr-Sauer模型计算得到的时均水平分速度与实验值吻合程度更好。

结合图6、7可以看出，采用修正后的Schnerr-Sauer模型更能准确反映水翼发生云空化时的流场情况。在x/c=0.4位置处，靠近翼型表面处流体具有较大的速度梯度，但远离壁面处流体速度趋于一致，与主流速度较接近。在x/c= 0.8位置处，靠近翼型表面处流体的时均水平速度出现负值，表明该区域的速度方向与主流方向相反，说明该区域内出现了反向射流，随着离壁面距离的增大，时均水平分速度也逐渐与主流速度达到一致；在x/c=1.2位置处，距离翼型表面不同位置处流场速度发生了急剧变化，出现了较大范围的逆向水平速度，表明该区域内形成了较大区域的漩涡结构。在x/c=0.8和x/c=1.2位置处模拟得到的速度场与实验值有较大差异，原因是所采用的SST k-ω模型本质上是标准双方程湍流模型，该类湍流模型预测能力具有一定的局限性。由于该类湍流模型对速度场进行时均化处理因而无法对空化区域内的微小漩涡结构进行准确预测。

图6　一个典型周期内实验和模拟的云空化空泡演变对比Fig.6 Comparisons of cavity shape evolution between simulation and experiment

图7　云空化条件下不同位置处时均水平分速度分布比较Fig.7 Comparisions of time-averaged u-velocity at different locations at cloud cavitation

5　结论

本文基于Schnerr-Sauer空化模型的思想和均相流假设建立了一种考虑不可凝结气体及湍动能脉动影响的空化模型（修正后的Schnerr-Sauer模型）。在SST k-ω湍流模型中引入与混合密度相关的修正函数对湍流粘度系数进行了修正，分别采用原始Schnerr-Sauer模型及修正后的Schnerr-Sauer模型对二维Clark-Y水翼绕流空化流场进行数值模拟，并与文献中的实验结果作对比，得到的主要结论有:

1）与原始的Schnerr-Sauer模型相比，采用修正后的Schnerr-Sauer模型计算得到的升阻力系数与实验值吻合程度更高，特别是捕捉空化初生时的升力系数及云状空化形成时的阻力系数所表现出的特征。

2）修正后的Schnerr-Sauer模型与原始模型计算出的云空化周期分别为35.9 ms和30.2 ms。修正后的Schnerr-Sauer模型能较清晰地模拟云状空泡的初生、发展、溃灭和脱落的全过程。

3）云状空化阶段，下游处（x/c=1.2）距离翼型表面不同位置处流场速度发生了急剧变化，出现了较大范围的逆向水平速度，但本文所采用的湍流模型在预测该处流动速度时出现了较大偏差。

［1］季斌，洪方文，彭晓星.二维水翼局部空泡脱落特性数值分析［J］.水动力学研究与进展，2008，23（4）:412-418. JI Bin，HONG Fangwen，PENG Xiaoxing.The numerical analysis of shedding characteristics on partial cavitation over 2D hydrofoils［J］.Chinese journal of hydrodynamics，2008，23（4）:412-418.

［2］SINGHAL A K，ATHAVALE M M，LI Huiying，et al. Mathematical basis and validation of the full cavitation model［J］.Journal of fluids engineering，2002，124（3）:617-624.

［3］ZWART P J，GERBER A G，BELAMRI T.A two-phase flow model for predicting cavitation dynamics［C］//Proceedings of the 5th international conference on multiphase flow.Yokohama，Japan，2004.

［4］SAUER J，SCHNERR G H.Development of a new cavitation model based on bubble dynamics［J］.Journal of applied mathematics and mechanics，2001，81（S3）:561-562.

［5］MERKLE C L，FENG J，BUELOW P E O.Computational modeling of the dynamics of sheet cavitation［C］//Proceedings of the 3rd International Symposium on Cavitation. Grenoble，France，1998.

［6］KUNZ R F，BOGER A D，STINEBRING D R，et al.A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction［J］.Computers&fluids，2000，29（8）:849-875.

［7］TAMURA Y，MATSUMOTO Y.Improvement of bubble model for cavitating flow simulations［J］.Journal of hydrodynamics，ser.B，2009，21（1）:41-46.

［8］DULAR M，BACHERT R，STOFFEL B，et al.Experimental evaluation of numerical simulation of cavitating flow around hydrofoil［J］.European journal of mechanics-b/fluids，2005，24（4）:522-538.

［9］LI D，GREKULA M，LINDELL P.A modified SST k-ω turbulence model to predict the steady and unsteady sheet cavitation on 2D and 3D hydrofoils［C］//Proceedings of the 7th International Symposium on Cavitation.Ann Arbor，Michigan，USA:University of Michigan，2009，16-20.

［10］FROBENIUS M，SCHILLING R，BACHERT R，et al. Three-dimensional unsteady cavitating effects on a single hydrofoil and in a radial pump measurement and numerical simulation［C］//Proceedings of the 5th International Symposium on Cavitation.Osaka，Japan，2003.

［11］LI Daqing，GREKULA M，LINDELL P.Towards numerical prediction of unsteady sheet cavitation on hydrofoils［J］. Journal of hydrodynamics，ser.B，2010，22（5）:741-746.

［12］LOHRBERG H，STOFFEL B，FORTES-PATELLA R，et al.Numerical and experimental investigations on the cavitating flow in a cascade of hydrofoils［J］.Experiments in fluids，2002，33（4）:578-586.

［13］ZNIDARCIC A，METTIN R，DULAR M.Modeling cavitation in a rapidly changing pressure field-Application to a small ultrasonic horn［J］.Ultrasonics sonochemistry，2015，22:482-492.

［14］ROOHI E，ZAHIRI A P，PASSANDIDEH-FARD M.Numerical simulation of cavitation around a two-dimensional hydrofoil using VOF method and LES turbulence model［J］. Applied mathematical modelling，2013，37（9）:6469-6488.

［15］杨琼方，王永生，张志宏.改进空化模型和修正湍流模型在螺旋桨空化模拟中的评估分析［J］.机械工程学报，2012，48（9）:178-185. YANG Qiongfang，WANG Yongsheng，ZHANG Zhihong. Assessment of the improved cavitation model and modified turbulence model for ship propeller cavitation simulation ［J］.Journal of mechanical engineering，2012，48（9）: 178-185.

［16］洪锋，袁建平，周帮伦.空泡半径非线性变化的空化模型及应用［J］.华中科技大学学报:自然科学版，2015，43（10）:15-20. HONG Feng，YUAN Jianping，ZHOU Banglun.Cavitation model considering non-linear variation of bubble radius and its application［J］.Journal of Huazhong university of science and technology:nature science edition，2015，43 （10）:15-20.

［17］REBOUD J L，STUTZ B，COUTIER O.Two-phase flow structure of cavitation:experiment and modeling of unsteady effects［C］//Proceedings of the Third Symposium on Cavitation.Grenoble，France，1998.

［18］WANG Guoyu，SENOCAK I，SHYY W，et al.Dynamics of attached turbulent cavitating flows［J］.Progress in aerospace sciences，2001，37（6）:551-581.

［19］HU Changli，WANG Guoyu，CHEN Guanghao，et al.A modified PANS model for computations of unsteady turbulence cavitating flows［J］.Science China physics，mechanics&astronomy，2014，57（10）:1967-1976.

［20］OCHIAI N，IGA Y，NOHMI M，et al.Numerical Prediction of Cavitation Erosion Intensity in Cavitating Flows around a Clark Y 11.7%Hydrofoil［J］.Journal of Fluid Science&Technology，2010，5（3）:416-431.

本文引用格式：

洪锋，袁建平，周帮伦，等.改进Schnerr-Sauer模型在水翼空化模拟中的评估分析［J］.哈尔滨工程大学学报，2016，37（7）:885-890.

HONG Feng，YUAN Jianping，ZHOU Banglun，et al.Assessment of improved Schnerr-Sauer model in cavitation simulation around a hydrofoil［J］.Journal of Harbin Engineering University，2016，37（7）:885-890.

Assessment of improved Schnerr-Sauer model in cavitation simulation around a hydrofoil

HONG Feng1，2，YUAN Jianping1，ZHOU Banglun1，SHI Yang1
（1.Research Center of Fluid Machinery Engineering and Technology，Jiangsu University，Zhenjiang 212013，China；2.Department of Mechanical Engineering，Eindhoven University of Technology，Eindhoven 5612AZ，Netherlands）

To enhance the capability of Schnerr-Sauer model in simulating cavitating flows，in this study，we developed an improved Schnerr-Sauer model based on the Rayleigh-Plesset equation and homogeneous flow assumption. The model considers the effects of turbulent fluctuation and noncondensable gas.The unsteady cavitating flow over a two-dimensional Clark-Y hydrofoil was numerically investigated combined with the SST k-ω turbulence model，in which the turbulence eddy viscosity is corrected.We obtain the time-averaged lift and drag coefficients，the cavity shape evolution at cloud cavitation，and its x-velocity profiles from these calculations.Compared with available experimental data in the literature，the time-averaged lift and drag coefficients predicted from the improved Schnerr-Sauer model agree better with the experimental results than with those of the original.In addition，the modified model can accurately predict the characteristics of the time-averaged lift and drag coefficients during different cavitation conditions.Moreover，the improved model can better simulate the inception，growth，shedding，and collapse of cloud cavitation than the original model.The overall results prove the reliability and accuracy of the improved Schnerr-Sauer model in cavitating flow simulations over a hydrofoil.

cavitating flow；hydrofoil；cavitation model；turbulence model；numerical simulation；drag coefficient；Schnerr-Sauer model

10.11990/jheu.201505010

S277.9；TH311

A

1006-7043（2016）07-885-06

2015-05-06.网络出版日期：2016-05-04.

国家自然科学基金重点项目（51239005）；江苏省普通高校研究生科研创新计划项目（KYLX_1040）；江苏高校优势学科建设工程项目（PAPD）.

洪锋（1988-），男，博士研究生；袁建平（1970-），男，研究员，博士生导师.

洪锋，E-mail:zjjaihf@163.com.

网络出版地址：http：//www.cnki.net/kcms/detail/23.1390.u.20160504.1435.002.html